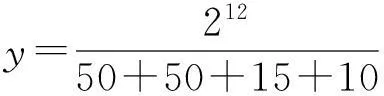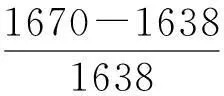高压输电线路故障数据预处理软件研制

张道荣， 徐鹏飞

(1.国网安徽省电力公司物资公司， 安徽　合肥　230061；

2.国网宣城供电公司， 安徽　宣城　242000)



高压输电线路故障数据预处理软件研制

张道荣1， 徐鹏飞2

(1.国网安徽省电力公司物资公司， 安徽合肥230061；

2.国网宣城供电公司， 安徽宣城242000)

摘要：本文研制的基于16位定点DSP的输电线路故障数据预处理软件采用了改进半波傅氏算法、提取衰减直流分量的近似算法和序分量算法，并对各算法在实现时的编程要点进行了说明。软件执行结果表明，文中所选取的算法和编制的程序能得到比较理想的滤波效果，满足工程实际对速度和精度的要求。

关键词：DSP；基波；衰减直流分量；序分量

0引言

随着数字技术的发展和计算机在电力系统继电保护中的应用，微机继电保护已普遍推广，而其中的保护原理一般用的是基频或某次谐波和正序、负序、零序等这些特征量。因此，需要对输入信号进行某种加工处理，以达到提取信号中的有用信息而去掉无用成分的目的，即进行滤波。实际电力系统运行经验表明，在微机继电保护中只有对从输电线路采集来的电压、电流信号进行快速而精确的滤波处理，才能使保护装置的可靠动作成为可能。继电保护系统所需的信息一经数据采集系统处理后，整个系统的实现将在很大程度上取决于该系统的数据处理能力。因此，需要寻找合理的数字滤波算法，使经过滤波之后的各分量满足微机继电保护的要求[1]。

1算法理论分析

1.1提取基波的算法

设电力系统故障电流有如下形式：

式中，Im(n)，φn分别为n次谐波的幅值和初相角。

在计算机上实现时，是对离散的采样值进行计算。用离散采样值表示的半波傅氏算法为：

(1-1)

(1-2)

式中，k表示从故障开始时的采样点序号；N为每个周期的采样点数。

如果输入信号中包含衰减非周期分量，将使半波傅氏算法的计算结果产生误差[2]，

(1-3)

(1-4)

消除wa和wb是将半波傅氏算法应用于快速保护的关键之一[2]。目前，为了消除衰减非周期分量的影响提出了许多算法，将各算法按计算精度、计算量和在DSP上实现时的难易程度的原则进行比较可知，差分算法增强了对高次谐波的响应，并使半波傅氏算法的幅频特性变坏；并联补偿法当未知时，根据线路的实际情况给出估计值会带来较大的误差；最小二乘算法当要求计算结果较精确时其计算量将会很大；卡尔曼滤波算法为了提高算法精度，应增加卡尔曼模型中谐波的次数，即状态方程中的状态数，而这将会使计算量非常大；半波傅氏算法与Mann-Morrison算法相结合的快速算法虽然其滤波效果大大优于半波傅氏算法，但仍不能满足精度要求且该算法无法求出N/2点的准确值。而半波再加两个采样点的改进半波傅氏算法计算精度高，运算量小，速度快，故本文采用了该算法来作为提取基波分量的算法。

半波再加两个采样点的改进半波傅氏算法的推导过程如下：

(1)取第一个数据窗，使t∈[0,T/2]，利用半波傅氏算法有：

(1-5)

令

(1-6)

则式(1～5)可以简化为：

(1-7)

(2)取延时ΔT为一个采样周期时间Ts取第2个数据窗，使t∈[ΔT,(T/2)+ΔT]，有：

(1-8)

令

(1-9)

为了提高算法的计算速度ΔT取为Ts较合适。一旦确定了每个周期的采样点数N，ΔT也就随之确定。同时，若谐波次数n和延时ΔT确定，ka，kb就成为两个常数。则式(1-8)可化简为[2]：

(1-10)

(3)延时2ΔT，取第3个数据窗，使t∈[2ΔT,(T/2+2ΔT)]，有：

(1-11)

由式(1-7)、式(1-10)、式(1-11)可以看出，式中的未知数A，B和e-αΔT只需作为中间变量，没有必要求出。其计算过程如下：

先消除A，B两个中间变量。

令：

Q=an′-kaan+kbbn

(1-12)

R=bn′-kabn-kbbn

(1-13)

X=an″-2kaan′+an

(1-14)

Y=bn″-2kabn′+bn

(1-15)

得：

(1-16)

消除衰减非周期分量对半波傅氏算法影响后的基波正弦项与余弦项振幅anc和bnc应为：

(1-17)

分析该算法的整个计算过程可知，半个周期后第3个采样间隔的计算量较大，但其计算时间用DSP实现所需时间仅为几十微秒，完全能够满足实际要求。

1.2求取衰减直流分量算法

假定离散化后的采样信号具有如下形式：

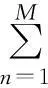
(1-18)

ΔT为采样时间间隔。令r=e-ΔT/τ，在一个周期内对x(k)求和得

(1-19)

引入第N+1点的采样值，在从2到N+1点的这一周期内求和并整理，同样有

(1-20)

由式(1-19)和(1-20)得

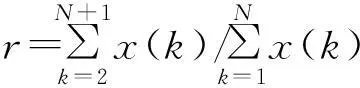
(1-21)

所以

τ=-ΔT/lnr

(1-22)

在对精度要求不高的场合，常采用近似算法。由式(1-19)得

(1-23)

其中，x(k)是对信号的离散化。

1.3序分量算法

因此可以得到序分量的计算式：

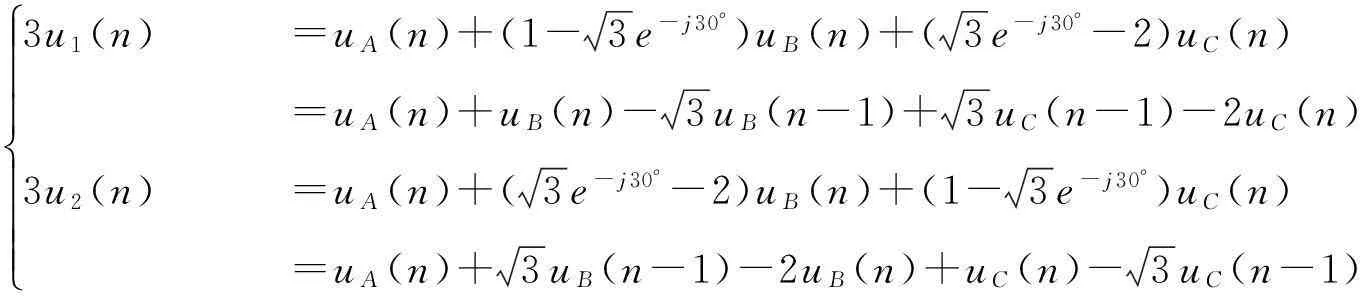
3u1(n) =uA(n)+(1-3e-j30°)uB(n)+(3e-j30°-2)uC(n) =uA(n)+uB(n)-3uB(n-1)+3uC(n-1)-2uC(n)3u2(n) =uA(n)+(3e-j30°-2)uB(n)+(1-3e-j30°)uC(n) =uA(n)+3uB(n-1)-2uB(n)+uC(n)-3uC(n-1)ìîíïïïïïï

(1-24)

式(1-24)只要2个采样周期就能算出正、负序分量，速度明显加快了。

2算法在CCS2上的实现要点

2.1改进半波傅氏算法的实现

(1)计算单个数据窗的基波余弦和正弦系数a1与b1值，结果即a1与b1值分别存入ab开始的连续两个存储单元中。

void Fourier( int ab[], int fXn[], int nFourier)

{

long a1=0;//存储基波余弦振幅

long b1=0;//存储基波正弦振幅

int k=0;//循环控制变量

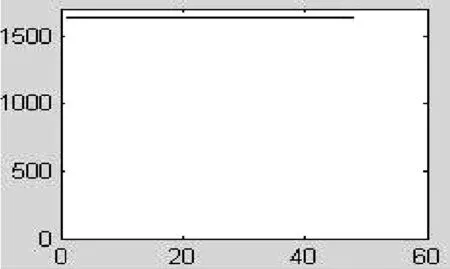
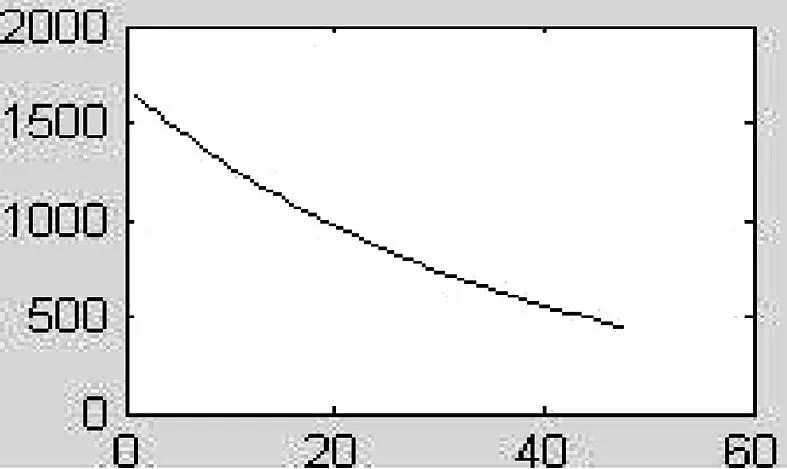
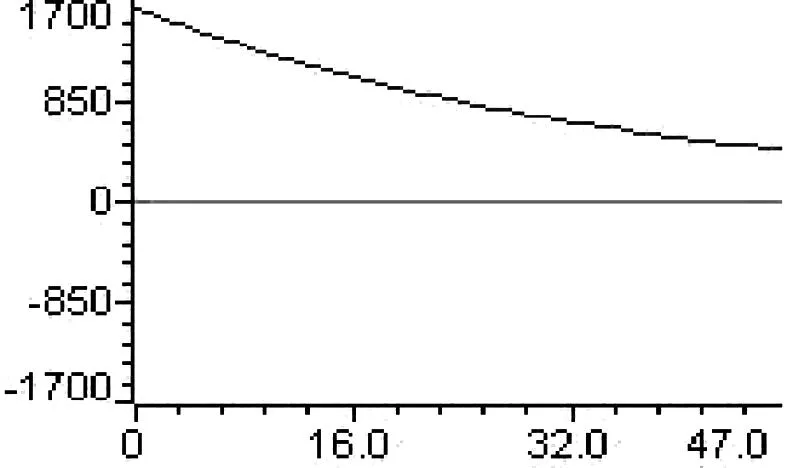
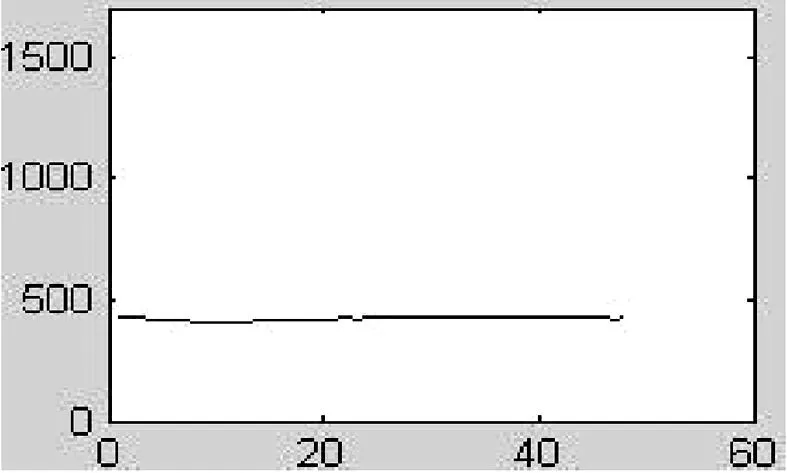
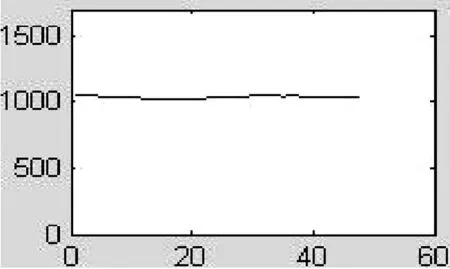
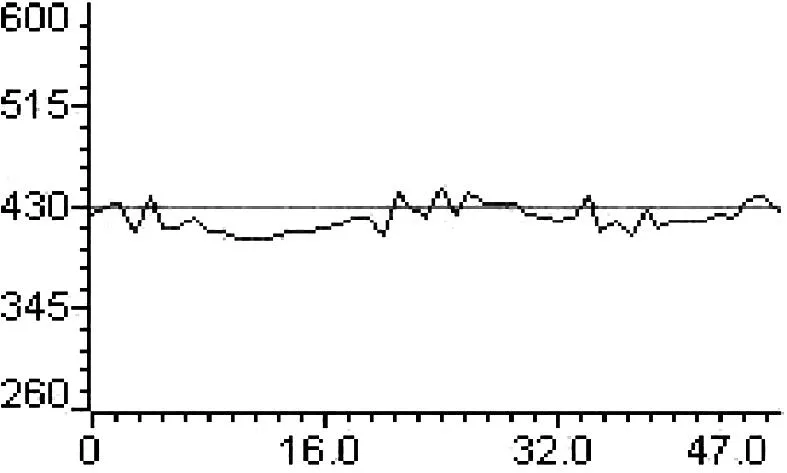
for(k=0;k

{

a1=a1+(long)(int)(*(fXn+k))*(long)(int)cosTable[k];

b1=b1+(long)(int)(*(fXn+k))*(long)(int)sinTable[k];

}

*ab=(int)(a1>>15);

*(ab+1)=(int)(b1>>15);

}

(2)计算并消除直流分量的函数NewArithmetic的注意事项。

半波傅氏算法的改进部分中的Q值由式(2-21)计算得到，其用C语言实现的方法如下：

temp=(long)(int)abNew[2]*(long)(int)max-(long)(int)abNew[0]*

(long)(int)ka+(long)(int)abNew[1]*(long)(int)kb;

temp>>=15;

Q=(int)temp;

2.2提取衰减直流分量的算法实现

根据第二章所述的近似计算衰减直流分量的算法理论，在实现的过程中先将由所对应的r值在MATLAB上离线计算出来，然后将计算得到的r值分别带入式(2-24)的分母从而计算出不同的所唯一对应的N个之和并存入数组便于计算时以查表的方式读取数据。采用这种近似算法和离线处理技术既保证了一定的计算精度又具有快速的特点，实现该算法的部分程序如下：

long firstSum=0;

long secondSum=0;

int temp,index,k,r;

intrTable[15]={17690,19140,20088,20756,21249,21630,21939,22186,22390,21537,22707,22833,22941,23042,23129};

for(k=0;k<24;k++)

{

firstSum+=(long)(int)dfXn[k];

secondSum+=(long)(int)dfXn[k+1];

}

r=(secondSum<<14)/firstSum - 15935;

if(r<220){index=(r+50)/100;}

else if(r<240) {index=(r-200)/20+2;}

else if (r<305){index=(r-240)/25+4;}

else if (r<340) {index=(r-300)/16+7;}

else if(r<365) {index=(r-340)/7+10;}

else {index=14;}

firstSum<<=10;

temp=(int)((long)firstSum/(long)rTable[index]);

上述程序中数组rTable中的值分别是τ等于30ms，40ms，…，170ms时所对应的N个rk之和。计算得到的直流分量值存储到变量temp中。

2.3序分量算法的实现

因采样点瞬时值的基波分量难以编程实现，故可采用先计算出采样点瞬时值的正序、负序、零序分量，再对各序分量进行滤波处理以提取基波幅值的方法来求取基波序分量值。计算第k个采样点瞬时值的正序分量的C程序代码如下所述，计算第k个采样点的负序和零序分量与计算正序分量时类似。

temp=(long)(int)table[0]*(long)(int)(fXnA[k]+fXnB[k])-(long)(int)table[1]*

(long)(int)(fXnB[k-2]-fXnC[k-2])- (long)(int)table[2]*(long)(int)fXnC[k];

temp>>=15;

3算法测试

被测试的输入信号A、B、C三相电压信号为：

(3-1)

其中，x是实际值，y是量化值。例如，数值50的量化值为1638。

本算例输入信号中含有衰减非周期分量的初值为100%基波幅值，之所以设置这样大的衰减非周期分量初值(在实际中属于比较严重情况)，就是为了人为增大衰减非周期分量对滤波算法的影响，来检验该算法的有效性[4]。

图1　MATLAB提取基波波形

图2MATLAB提取直流波形

图3DSP提取基波波形

图4　DSP提取直流波形

图5MATLAB提取正序电压波形

图6MATLAB提取负序电压波形

图7　MATLAB提取零序电压波形

图8DSP提取正序电压波形

图9DSP提取负序电压波形

图10　DSP提取零序电压波形

将DSP上的结果波形与在MATLAB上进行精确计算得到的波形进行比较可知，本文研制的基于DSP的输电线路故障数据预处理软件具有较高的精度，而且程序执行速度较快，符合电力系统继电保护工程实际中对速度和精度的要求。

4结论

对于各种傅氏算法而言，最大的问题就是如何滤除故障暂态过程中普遍存在的衰减直流分量。本文结合算法的计算速度、精度及计算量等因素，在提取基波时最终采用了改进半波傅氏算法，即利用半波采样数据另加2个采样点来计算基波电压幅值，该算法具有速度快、精度高的特点；提取直流分量时，本文采用的是在全波傅氏算法的基础上增加一个采样点的算法，该算法能较好的提取出衰减直流分量初始值且精度也较高；序分量算法采取的是其改进算法，即在每周波采样24点时，要计算一个采样点的序分量只需得到前两个序分量的值即可，提高了计算速度，精度也较高。通过对程序的验证，表明本文所研制的基于DSP的输电线路故障数据预处理软件是满足工程实际要求的。

参考文献：

[1] 杨畅.新型数字保护的构想与分析[J]. 宁夏电力, 2005(Z1):155-157.

[2] 郗忠梅.智能型相敏保护在煤矿中的开发及应用[D]. 山东农业大学硕士论文,2004.

[3] 黄华国，李建安.序分量算法的分析[J].水利科技,2003(4).

[4] 丁书文，张承学，龚庆武，肖迎元.半波傅氏算法的改进——一种新的微机保护交流采样快速算法[J].电力系统自动化，1999(5).

[责任编辑：朱子]

Fault Data Preprocessing Software Development of High Voltage Transmission Line

ZHANGDao-rong1,XUPeng-fei2

(1.MaterialsCompanyofStateGridAnhuiElectricPowerCorporation,Hefei230061,China;2.StateGridXuanchengPowerSupplyCompany,Xuancheng242000,China)

Abstract:This paper develops the software of transmission line fault data preprocessing based on 16 fixed DSP which adopts the improved half-wave Fourier algorithm, extracting decaying DC components approximation algorithm and sequence component algorithm, and explains the programming essentials for realizing each algorithm. The software execution results indicate that the algorithm and program can gain the ideal filtering effect, and meet the demands of project practice on the speed and the precision.

Key words:DSP; fundamental wave; decaying DC component; sequence component

中图分类号：TP391.75

文献标识码：A

文章编号：1672-9706(2016)01- 0108- 06

作者简介：张道荣(1973-)，男，安徽淮北人，高级工程师，国网安徽省电力公司物资公司(安徽皖电招标公司)副总经理，从事电气工程技术及物资管理等工作。徐鹏飞(1985-)，男，湖北天门人，工程师，国网宣城供电公司，从事通信工程技术及相关管理工作。

收稿日期：2016- 02-15