基于卡尔曼滤波的空气质量指数预测方法
南亚翔,李红利,修春波,张洪志
(1.天津工业大学电气与自动化学院,天津 300387;
2.天津工业大学电工电能新技术天津市重点实验室,天津 300387;
3.中国石油大港油田原油运销公司,天津 300280)
基于卡尔曼滤波的空气质量指数预测方法
南亚翔1,2,李红利1,2,修春波1,2,张洪志3
(1.天津工业大学电气与自动化学院,天津 300387;
2.天津工业大学电工电能新技术天津市重点实验室,天津 300387;
3.中国石油大港油田原油运销公司,天津 300280)
摘要:分析了卡尔曼滤波预测空气质量指数的机理,用ARMA算法为卡尔曼滤波建立模型,提出了将RBF神经网络融合于卡尔曼滤波的方法,实现对空气质量指数的混合预测。根据空气质量指数时间序列的特点,建立了自回归预测模型,进而建立卡尔曼滤波的状态方程和测量方程。采用随机梯度逼近训练算法训练RBF神经网络,用RBF神经网络的输出作为卡尔曼滤波测量方程的观测值。融合了RBF神经网络后的卡尔曼滤波预测方法减少了单一方法的延迟现象,使同种性质的误差累积减小,提高了预测精度。对AQI序列预测的仿真显示融合后的卡尔曼滤波方法优于单一的卡尔曼滤波方法,亦优于现已广泛应用的BP神经网络预测方法。
关键词:卡尔曼滤波;空气质量指数;预测;ARMA;RBF神经网络
近年来城市空气污染严重,民众对空气质量日益关注。环保部门对AQI(空气质量指数)数据进行通报时,由于大气空间属于纯滞后系统,因此通报的数据具有滞后性,实时性较差,不能够满足一些户外作业和特定工作人员的需求。AQI指数预测可以解决通报数据滞后性问题。由于空气污染物浓度受到污染排放源、理化生过程和复杂下垫面等因素的影响,因此具有强非线性特性[1]。人工神经网络是描述非线性系统的有效工具,其中BP神经网络作为使用最为广泛的神经网络之一,有很强的泛化能力和容错能力,亦能够很好地描述污染指数与其影响因子之间的非线性关系,十分简单可行,已经被广泛应用在PM10、SO2、NOx等污染物浓度的预测当中[2-6]。但BP神经网络具有误差较大,训练时容易陷入局部最小值等缺点,预测效果不佳[7]。本文分析了ARMA建模方法和卡尔曼滤波数据预测及融合的机理,提出了将RBF(径向基函数)神经网络预测数据融合在卡尔曼滤波的方法,克服了单一方法预测的不足,提高了AQI指数预测的精度。
1基于卡尔曼滤波的AQI指数预测
1.1由ARMA模型建立线性离散动态系统模型
时间序列最优预报的基本数学模型是自回归滑动平均模型[8],在ARMA模型中,时间序列{x(t)}具有以下形式:
xt-φ1xt-1-…-φpxt-p=at-θ1at-1-…θqat-q
(1)

(2)
xt=φ1xt-1+φ2xt-2+φpxt-p+εt
(3)
则系统的状态方程及测量方程可以写为:
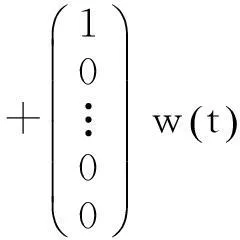
(4)
(5)
1.2卡尔曼滤波的基本原理
卡尔曼滤波本质上是给出了一种递推算法,由实时获得的离散观测数据,对系统状态进行线性、无偏及最小误差方差的最优估计[9]。应用卡尔曼滤波首先要建立线性模型。通常情况下,线性离散动态系统可以由以下状态方程和观测方程表示:

(6)
Z(t)=H(t)X(t)+v(t)
(7)
其中:t是离散时间;Φ(t,t-1)是从t-1时刻到k时刻的状态转移矩阵;Γ(t,t-1) 是从t-1时刻到t时刻的激励转移矩阵;H(t)是t时刻的预测输出转移矩阵;w(t)是p维系统噪声向量;v(t)是m维观测噪声向量;x(t)是n维状态向量;Z(t)是m维观测向量。
在卡尔曼滤波方程中,假设w(t)、v(t) 为高斯白噪声。它们的协方差矩阵分别设为Q(t)和R(t),一般情况下Q(t)和R(t)的值按经验取。卡尔曼滤波首先针对无控制输入系统求解,再通过叠加确定性求解,最终得到的递推预测方程如下:

(8)
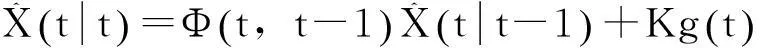

(9)
(10)
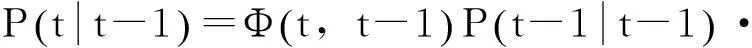
(11)

(12)
1.3基于神经网络观测值的获取
为了克服用单一方法对空气污染指数预测的不足,本文将神经网络获得数据的观测值Z(t)代入到卡尔曼滤波方程中,从而将神经网络融合在卡尔曼滤波当中,实现混合预测。
神经网络系统实质上是由大量的神经单元广泛地互相连接而形成的复杂的网络系统,具有学习功能。可以处理难以用模型或规则描述的过程和系统,并且具有很强的容错性[11,12]。本文采用RBF神经网络对空气污染指数数据进行预测。
RBF神经网络是一种前向型神经网络,网络由三层组成,即输入层、单层的非线性处理神经元和输出层。与现今应用较为广泛的BP神经网络相比,具有更快的学习收敛速度,良好的泛化能力,结构简单,有最佳逼近性能和全局最优特性等优点。RBF的输出层一般满足:
(13)

用已知的AQI数据序列作为训练样本集,为了避免因为从输出数据集中选取大量的中心,进而产生相对庞大的网络,本文采用随机梯度训练算法。
随机梯度法在训练RBF神经网络时使输出层的加权值w、中心点值c和扩展参数同步进行有导师学习,即
(14)
(15)

(16)
其中:
(17)
(18)

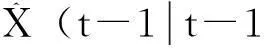

2数据来源
根据2012年中华人民共和国环境保护部发布的《环境空气质量指数(AQI)技术规定(试行)》,地级以上(含地级)环境保护行政主管部门或其授权的环境监测站开始向公众对AQI指数进行实时报和日报。研究使用的数据为中华人民共和国环境保护部数据中心发布的天津市2013年上半年连续90h的AQI数据。

表1 空气质量指数及相应质量级别
空气质量指数级别根据表1规定进行划分。与之前广泛使用的空气污染指数(API)相比,环境空气质量指数将可吸入细颗粒物(PM2.5)等污染物纳入了测量通报范围,相比之下AQI评价结果更真实地反映了空气质量实际情况。随着纳入考核的污染物种类的增多和计算方法复杂程度的加大,AQI指数受到更多因素的影响,具有较强的非线性特性。
3对AQI指数预测的仿真和分析
3.1卡尔曼滤波对AQI指数的预测
本文选取了天津市2014年上半年某星期连续90h的时报AQI指数作为实验数据。由于每年相同时节影响AQI指数的自然因素(大气温度、湿度等)较为相似,选取天津市2013年上半年1—5月份时报AQI指数作为RBF神经网络的训练样本,6月份的时报AQI指数作为测试样本,用于对RBF神经网络预测性能的检验。


由图3可以看出,通过ARMA算法建立模型的卡尔曼滤波方法能够对AQI指数进行预测。预测的结果能够大体反映AQI指数的变化趋势,但存在较大的滞后延迟现象,致使预测结果的误差较大,并未达到理想的预测结果。
3.2基于BP神经网络对AQI指数的预测
用BP神经网络对AQI指数进行预测,得到的预测样本如图4。

由图4可见,BP神经网络预测算法在某些点处有较强的非线性逼近能力,具有一定的预测能力和预测精度,但在指数波动较大的极点处,误差较大。即空气指数的波动对BP神经网络的泛化能力有影响,影响了预测的效果和预测精度。
3.3基于RBF神经网络和卡尔曼滤波混合算法对AQI指数的预测
将RBF神经网络的预测结果作为卡尔曼滤波方程的观测值,实现AQI指数的混合预测,所得预测结果如图5所示。

由图5可见,卡尔曼滤波能够将ARMA方法和RBF神经网络方法进行融合,从而可进一步优化预测结果,预测结果优于单一采用RBF神经网络的预测结果和单一的卡尔曼滤波预测方法。融合的预测方法与RBF神经网络预测结果相比,延迟现象得到了极大的改善;与BP神经网络预测方法相比,在数据序列极值点的预测结果误差大大减小,预测效果有明显改善。不同方法预测误差指标如表2所示。
从表2误差比较结果可见,BP神经网络对AQI指数的预测结果有较大的误差,这是因为单一的BP神经网络中神经元对历史信息的记忆能力和利用率有限,对数据原状态的保持能力不佳,从而增加了神经元状态错误变化的机率。单一的卡尔曼滤波预测方法具有单一预测机理所造成的同一性质误差的累积,因此误差亦较大。融合的卡尔曼滤波方法将卡尔曼滤波和RBF神经网络结合,吸收了RBF神经网络良好的泛化能力、学习速度快、容易适应新数据的优点和卡尔曼滤波预测模型所利用的信息量较少、对初始量数据要求不高的优点,大大增强了预测的精度,从而减少了预测误差。

表2 不同方法预测性能指标
4结论
(1) 本文提出并分析了卡尔曼滤波方法对AQI指数的预测机理,对不同预测方式的预测性能进行了分析比较。用ARMA模型建立卡尔曼滤波的状态方程和观测方程,利用RBF神经网络的预测值作为卡尔曼滤波方程的观测值,进而用卡尔曼滤波方法将ARMA和RBF神经网络融合在一起,实现了AQI指数的混合预测。
(2)仿真实验结果验证了混合预测方法的有效性,该混合预测方法能有效减小单一预测方法造成的误差积累,并减少极值点等有较大波动数据点的误差。融合后的方法获取了2种方法的优点,预测结果十分理想。
参考文献:
[1]李小飞,张明军,王圣杰,赵爱芳,马潜. 中国空气污染指数变化特征及影响因素分析[J]. 环境科学,2012(6):1936-1943.
[2]白晓平,张启明,方栋, 等.人工神经网络在苏州空气污染预报中的应用[J].科技导报, 2007, 25(3): 45-49.
[3]曹兰.空气中PM10浓度的BP神经网络预报研究[J].环境研究与监测, 2010, 23(2): 29-32.
[4]王俭, 胡筱敏, 郑龙熙, 等. 基于BP模型的大气污染预报方法的研究[J].环境科学研究, 2002, 15(5): 62-64.
[5]白鹤鸣,沈润平,师华定,董钰春. 基于BP神经网络的空气污染指数预测模型研究[J]. 环境科学与术,2013(3):186-189.
[6]周秀杰,苏小红,袁美英. 基于BP网络的空气污染指数预报研究[J]. 哈尔滨工业大学学报,2004(5):582-585.
[7]Kalman R E. A New Approach to Linear Filtering and Prediction Theory. Trans ASME Journal of Basic Eng . 1960
[8]张贤达. 确定ARMA模型MA阶数的一种方法[J]. 自动化学报,1994(1):80-84.
[9]修春波,任晓,李艳晴,刘明凤. 基于卡尔曼滤波的风速序列短期预测方法[J]. 电工技术学报,2014(2):253-259.
[10]王学林,周俊,姬长英,姜莉. 基于卡尔曼滤波的RBF神经网络和PD复合控制研究[J]. 计算机测量与控制,2009(8):1551-1553,1573.
[11]刘进宝,丁涛. 基于径向基函数神经网络的风速预测[J]. 太阳能学报,2012(7):1131-1135.
[12]Y. F. Sun,Y. C. Liang,W. L. Zhang,H. P. Lee,W. Z. Lin,L. J. Cao. Optimal partition algorithm of the RBF neural network and its zapplication to financial time series forecasting[J]. Neural Computing and Applications, 2005 (1).
Prediction Method of Air Quality Index Based on Kalman Filtering Fusion
NAN Ya-Xiang1,2, LI Hong-Li1,2, XIU Chun-Bo1,2, ZHANG Hong-Zhi3
(1.Tianjin Polytechnic University, College of Electrical Engineering and Automation, Tianjin 300387, China)
Abstract:The prediction mechanism ofKalman filtering for air quality index was analyzed. And a hysteretic neural network was proposed to predict the air quality index series. State equation for Kalman filter was established by ARMA model. The hybrid prediction of air quality index, combining Kalman filter and RBF neural network was proposed. According to the characteristic of air quality index series, autoregressive model was established. And then, the measurement equation and the state equation of Kalman filter were established as well. Stochastic gradient approximation method was applied to train RBF neural network. The output of RBF neural network was regarded the observed value by Kalman filter. Hybrid prediction’s main advantages included preventing forecast delay caused by the single prediction mechanism and precise forecasting. The results of predicting air quality index simulation showed that the hysteretic Kalman filter had better prediction performance than original Kalman filter, and the hysteretic Kalman filter was also superior to BP neural network.
Key words:Kalman filter; air quality index; prediction; ARMA; RBF neural network
中图分类号:X 823
文献标志码:A
文章编号:1673-9655(2016)03-0080-05
作者简介:南亚翔(1990-),男,辽宁铁岭人,硕士研究生,主要研究智能控制系统与数据挖掘。
基金项目:国家自然科学基金项目(No.61203302);天津市应用基础与前沿技术研究计划项目(14JCYBJC18900)。
收稿日期:2015-10-10

