基于高斯算法的小行星固定时间拦截

丁文哲，杨　虹，陈　峰

(装备学院， 北京　101400)



基于高斯算法的小行星固定时间拦截

丁文哲，杨虹，陈峰

(装备学院， 北京101400)

摘要：为了防止未来有小行星撞击地球，想要对小行星实施固定时间拦截；首先根据给定的地球与小行星的撞击点位置以及小行星与地球撞击点的速度，建立小行星的轨道模型；利用小行星与地球的轨道模型预推出拦截卫星发射点的位置，再利用高斯算法建立卫星的固定时间拦截轨道模型，并计算卫星发射速度，以及碰撞后小行星的速度；最后，对所建立的模型进行数值仿真。仿真结果表明：若地球将与小行星发生碰撞，则拦截卫星将按拦截轨道运行固定时间后成功与小行星拦截相撞。

关键词：轨道模型；固定时间拦截；高斯算法

Citation format:DING Wen-zhe, YANG Hong, CHEN Feng.Fixed Time Interception of Asteroids Based on Gauss Algorithm[J].Journal of Ordnance Equipment Engineering,2016(3):106-110.

2015年7月20日凌晨，一颗名为2011UW-158的小行星与地球擦肩而过，据说它含有1亿吨的白金而备受人们关注，虽然在安全距离上飞掠地球，但是距离只为地月距离的6.4倍。近年来，小行星安全事件越来越受到人们的关注。就在2013年2月15日,一颗明亮的火流星坠落在距离我国不远的俄罗斯城市车里雅宾斯克境内,这件从1908年西伯利亚通古斯事件以来有记录的最大陨星撞击地球事件,让我们记忆犹新。最近，许多科学家在Nature和Science上发表的研究结果表明,比上述陨星体积更大的或者相同的小行星在将来与地球发生撞击的可能性会比之前预想的可能性大得多。NASA的科学家在2014年曾宣称在2040年很大可能会有一颗名为2011 Ag5的小行星对地球进行撞击，也许在未来也会遭遇6 500万年前恐龙所遭遇过的灭顶之灾。那么,发射卫星对未来可能再次到来地球的小行星进行拦截,改变其运动轨道显得尤为重要。

本文以给定地球与小行星的撞击点和在这个撞击点处的小行星速度为例,建立出小行星的轨道模型,并判断出卫星发射点位置;然后建立出卫星的固定时间拦截轨道模型,并通过仿真验证了拦截轨道可行。

1小行星轨道模型

1.1建立太阳坐标系

根据地球轨道,建立太阳坐标系，以太阳为坐标系原点，x轴指向地球的春分点，y轴在地球的运行轨道平面内，绕x轴逆时针旋转90°得到，由右手定则确定出z轴位置。在本文中假设撞击点A位于第一象限平面内，撞击点位于其他3个象限内的情况只需要将坐标轴旋转就可以同理解算。此时，地球、小行星和拦截卫星三者轨道的大致示意关系，如图1所示。

图1　轨道示意图

1.2小行星轨道六根数

由活力公式得小行星的半长轴为

(1)

(2)

由rA=a3(1-e3cos(E3 A))得A点平近地点角为

(3)

求出小行星从近地点运行到A点的时间为

(4)

根据小行星的轨道法向量与升交点矢量得小行星的轨道倾角和升交点赤经为

(5)

由rA求得小行星在A点的真近地点角为

(6)

A点为小行星的降交点,所以A点的纬度幅角为180°，可得小行星的近地点幅角为

(7)

1.3卫星与小行星撞击点的位置

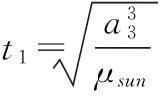
(8)

得到B点的真近地点角：

(9)

利用上面求得的结果，可以得到B点的纬度幅角为u3B=ω3+f3B。

利用球面三角形公式得出在太阳坐标系下撞击点B的位置为

(10)

1.4卫星与小行星撞击点处小行星速度

拦截点B处小行星速度大小为

(11)

(12)

求得拦截点B速度方向与升交点方向的夹角为

(13)

利用球面三角形公式得出拦截点B小行星速度分量：

(14)

2卫星发射点位置

由于地球在t2时间内运行的平近地点角不能确定,就需要分四种情况来讨论卫星发射点位置C,如图2所示。

将Eearth去除周期倍,使其大小落在[0,2π)内。如果θ1+Eearth≤90°，那么就为图2(a)。如果90°<θ1+Eearth≤180°，那么就为图2(b)。如果180°<θ1+Eearth≤270°，那么就为图2(c)。如果270°<θ1+Eearth≤360°，那么就为图2(d)。

经分析情型1、2、3、4后，确定C点位置速度均为

(15)

其中vearth可由活力公式得到:

图2　卫星发射点判断图

3固定时间拦截的轨道模型

3.1拦截轨道六根数

首先由高斯迭代算法求得ΔE与Δf,从而得拦截轨道半长轴与半通径为

(16)

(17)

由C,B点矢量求得拦截轨道面法向量为

(18)

利用Z轴单位向量与轨道面法向量叉乘得拦截轨道升交点矢量为

(19)

则根据拦截轨道的轨道法向量与升交点矢量求得拦截轨道的轨道倾角和升交点赤经分别为

(20)

拦截轨道偏心率：

(21)

由rC求得拦截轨道在C点处的真近地点角为

(22)

C点为拦截轨道的升交点,所以C点的纬度幅角为0度,可得拦截轨道的近地点幅角为

(23)

3.2卫星相对于地球的发射速度

由活力公式求得拦截轨道C点处卫星的初始速度为

(24)

求出vC与rC的夹角：

(25)

得发射点C速度方向与升交点方向的夹角：

(26)

根据球面三角形公式得到发射点C卫星速度投影分量为

(27)

从而求得在太阳系中给卫星提供的速度增量为

(28)

在地球惯性坐标系中给卫星提供的速度增量为

(29)

建立卫星的能量守恒方程：

(30)

求得卫星相对于地球的发射速度为

(31)

3.3撞击后小行星速度

由活力公式得拦截轨道B点处卫星的速度为

(32)

求出vB与rB的夹角为

(33)

拦截轨道在拦截点B处的纬度幅角为

(34)

得到拦截点B处卫星速度方向与升交点矢量方向的夹角：

(35)

根据球面三角形公式得到拦截卫星在拦截点B处速度投影分量：

(36)

拦截后，发射出的卫星将降落于小行星上与小行星一起运动,这样就会改变小行星的轨道也可以对小行星进行探测,此时建立小行星的动量守恒方程：

(37)

得拦截后在拦截点B点小行星的速度：

(38)

4仿真验证

4.1仿真条件

4.2仿真结果及分析

按照文中的方法仿真得出行星与地球的运动轨迹，两者的运动轨迹曲线如图3所示。

图3　行星地球轨迹图

图中标示了行星的运动轨迹和地球的运动轨迹，由图3可以看出按文中方法可以根据给定初始条件，计算模拟出行星与地球的运行轨迹，符合任务要求，两者在一段时间后相撞。

图4为地球与行星间距离随时间的变化图。由图4中地球与小行星之间的距离数据可以更加直观明显看出，地球与行星会在43 d后相撞。下面图5为根据固定时间拦截方式模拟仿真的行星、地球与卫星三者的运行轨迹。

图4　地球与小行星间距离变化图

图5　卫星拦截轨迹图

图5中标示了卫星的拦截轨迹和行星的运动轨迹、地球的运动轨迹，由图5可以看出按文中的固定时间拦截方法，根据任务需要的时间来对行星进行拦截，可以计算模拟出卫星的固定时间拦截轨迹，很好的符合了任务要求，卫星与行星会在一段时间后相撞。图6为卫星与行星间的距离随时间变化图。

图6　卫星与小行星间距离变化图

由图5中两者间的距离数据可以更加直观明显看出，卫星按轨迹飞行30 d后将会与行星相撞，证明了文中所述的固定时间拦截方法是一种很好的轨道计算方式，按这种方式计算出的发射速度进行发射，将会满足任务需求。

最后根据文中所述动量守恒的计算方式可以很容易得出行星与卫星相撞后一起飞行的速度，根据拦截点位置与行星与卫星相撞击后的速度，按文中确定行星轨迹方式可以得到撞击后行星的运行轨迹，得出撞击后行星轨迹偏移原轨道。

5结束语

本文主要针对防止地球与行星相撞的问题进行了研究，提出了引用高斯迭代算法对小行星实施固定时间拦截的想法。首先建立了地球、小行星轨道模型；接着利用高斯迭代算法建立了固定时间拦截轨道模型，计算出所需要的拦截卫星发射速度，以及碰撞后小行星速度；最后就高斯迭代算法的具体实现进行了数值仿真，验证了该方法的有效性。

参考文献：

[1]李飞,孟林智,王彤,邹乐洋.国外近地小行星撞击地球防御技术研究[J].航天器工程,2015(2):87-95.

[2]何亮.小行星：为何会有一颗Pt的“心”[N].科技日报,2015-07-23(005).

[3]王超,谭守林,李国庆.定时拦截在轨拦截器机动轨道设计与优化[J].指挥控制与仿真,2014(6):107-110.

[4]党露,和兴锁,徐卫昌.固定时间轨道拦截的制导方法研究[J].飞行力学,2014(3):266-269.

[5]刘军.小行星撞地球躲避方法[J].宜宾科技,2014(1):25.

[6]张舒阳.卫星轨道方程的数值积分方法[D].长沙：国防科学技术大学,2009.

[7]周旋.弹道目标轨道确定方法研究[D].西安：西安电子科技大学,2014.

(责任编辑杨继森)

Fixed Time Interception of Asteroids Based on Gauss Algorithm

DING Wen-zhe, YANG Hong, CHEN Feng

(The Academy of Equipment Command & Technology，Beijing 101400, China)

Abstract:In order to prevent the collision of asteroid and earth in the future, measure of intercepting incoming asteroid in a fixed time was proposed. First, we established a model of the asteroid’s orbit by the assumed impact point position and the speed of the asteroid at the impact point and determined the position of intercept satellite launching point. Secondly, we built a fixed time interception trajectory model, using Gauss algorithm to calculate the speed which launches the intercept satellite and the speed after collision the asteroid. The efficiency of the presented model was demonstrated by numerical simulation. Simulation results show that if the earth will collide with an asteroid, and the intercept satellite which track the intercept orbit will intercept the colliding with the asteroid successfully after a fixed time.

Key words:orbit model; fixed time intercept; Gauss algorithm

文章编号：1006-0707(2016)03-0106-05

中图分类号：V529.1；TJ861

文献标识码：A

doi:10.11809/scbgxb2016.03.026

作者简介：丁文哲(1992—)，男，硕士，主要从事太空观测研究。

收稿日期：2015-08-21；修回日期：2015-09-11

本文引用格式：丁文哲，杨虹，陈峰.基于高斯算法的小行星固定时间拦截[J].兵器装备工程学报，2016(3):106-110.

【信息科学与控制工程】