关于Li掺杂非磁性半导体SnO2的磁性研究

刘昱　闫羽

[摘要]采用基于密度泛函理论的第一性原理计算方法分析Li掺杂SnO2材料，研究了Li替代Sn原子掺杂和氧空位缺陷对SnO2体系电子结构和磁性的影响。计算结果表明，含有氧空位的SnO2体系是非磁性态，而含有氧空位的Li替代掺杂SnO2体系的基态是磁性态。Li替代Sn掺杂使SnO2体系产生磁性，并且磁矩随掺杂原子浓度的增加而增大，氧空位缺陷使替代掺杂的SnO2体系的形成能降低，这表明有氧空位的情况下，替代掺杂更容易形成。电子结构分析表明，体系磁矩的产生主要来源于替代原子周围的O原子p轨道的贡献，从理论上解释了产生磁矩的原因。

[关键词]第一性原理 Li掺杂 SnO2 磁性

[中图分类号]O483 [文献标识码]A [文章编号]1009-5349（2016）06-0144-03

最近关于非磁性离子掺杂稀磁半导体材料的磁性研究引起了物理学界的广泛关注。稀磁半导体作为一种最有希望实现自旋电子学应用的功能性材料，可以通过掺杂导致磁性。氧化物半导体SnO2具有高透光性、高化学稳定性和高导电性，被广泛应用于气体传感器、透明导电电极、催化剂载体和太阳能电池等方面。非磁性离子掺杂可以有效地消除非内禀磁性所产生的影响，而且SnO2属于宽带隙半导体，能够实现n型载流子重掺杂（在温度为300k时，禁带宽度达3.6eV）。实验研究发现，非磁性的SnO2掺杂非磁性的元素Li后，具有铁磁性，其饱和磁矩随掺杂Li离子浓度的增加而增加。目前关于Li掺杂SnO2产生磁性规律的机制还没有报道。本文采用基于密度泛函理论的第一性原理计算方法分析Li掺杂SnO2材料，研究了Li替代和氧空位对SnO2电子结构和磁性的影响，并进行了对比分析，得到了有意义的结果。

一、理论模型和计算方法

（一）理论模型

理想的SnO2属于四方金红石结构，每个Sn原子周围包含有6个氧原子，Sn原子处于氧八面体中心。计算Li掺杂SnO2时，我们构建了一个包含有72个原子的2×2×3超晶胞结构，如图1所示。选取三种不同的掺杂离子浓度，分别为4.16%、8.33%和12.5%进行计算分析，并考虑氧空位对掺杂体系磁性的影响。取SnO2的实验晶格常数a=b=0.4737nm，c=0.3186nm，α=β=γ=90°。

（二）计算方法

本文所有的计算工作采用的是维也纳工业大学开发的VASP程序软件包，计算中价电子和芯电子之间的相互作用采用了基于密度泛函理论的缀加平面波法（PAW）进行处理，对于交换关联效应采用了广义梯度近似（GGA）的方法进行描述。体系的平面波截断能取为400eV，布里渊区的特殊点积分采用的是Monkhost-Pack-method对布里渊区求和。为了使计算结果更为准确，首先对Li掺杂SnO2进行结构优化，然后对结构优化后的体系进行自旋极化计算，几何优化的收敛标准是连续循环的能量差为1×10-3eV/atom。计算中把Sn：5S25p2，O：2S2P4，Li：2S1P0作为价电子。

二、计算结果与讨论

（一）掺杂原子和氧空位位置的选取

从图1中可以看出，Li替代Sn原子掺杂的位置，选取了三个不同的位置，Sn23O48（掺杂离子浓度4.16%）选取Li1，Sn22O48（掺杂离子浓度8.33%）选取Li1 Li2，Sn21O48（掺杂离子浓度12.5%）选取Li1 Li2 Li3。Sn24O47氧空位的位置选取在Vo1，Sn23O47氧空位尝试选取了12个不同的位置如图2所示。Sn22O47氧空位仍选取在Vo1。构建好超晶胞结构，然后首先对体系进行结构优化，再进行自旋极化计算。

（二）缺陷形成能（Ef）的计算

缺陷形成能（Ef）的大小可以直接反映出掺杂体系在各种不同环境下，掺杂缺陷形成的难易程度和掺杂体系的结构稳定性等。本文通过计算Li掺杂SnO2缺陷的形成能，进一步了解Li掺杂SnO2体系的结构。本文在富Sn（Sn-rich）或富O（O-rich）两个条件下计算Li掺杂SnO2体系的Li掺杂缺陷的形成能（Ef）。

（三）计算结果分析

MLi代表掺杂原子Li的磁矩，MO代表掺杂体系中所有O原子的总磁矩，MSn代表掺杂体系中所有Sn原子的总磁矩。

1.氧空位对纯SnO2体系的影响

氧空位产生的位置如图1中Vo1蓝色球位置所示，比较分析纯的Sn24O48体系和含有一个氧空位的Sn24O47体系的总态密度图，如图3所示。从计算结果中可知，纯的Sn24O48体系和含有一个氧空位的Sn24O47体系的总磁矩为0，体系均为非磁性的，从态密度图和自旋密度图中分析可知，由于氧空位的作用，使含有一个氧空位的Sn24O47体系产生了自旋非劈裂的杂质态，自旋向上和自旋向下的态密度对称，体系所有原子未被极化。

2.不同掺杂离子浓度对SnO2体系的影响

比较分析一个替代、两个替代和三个替代的掺杂情况，掺杂离子浓度分别为4.16%、8.33%和12.5%时，SnO2体系的磁性。从磁矩分布表1中可以看出，掺杂体系均为磁性态，MLi代表掺杂原子Li的磁矩，体系的磁矩主要由掺杂原子Li贡献。从三种不同掺杂情况的态密度图和自旋密度图中可以看出，都是替代原子Li在价带顶附近产生了杂质态，导致价带产生了空穴，掺杂体系表现为磁性态，掺杂原子Li周围的O原子被极化，费米能级附近的杂质态主要由替代原子周围的O原子的p轨道组成，因此体系磁矩的产生主要由O原子贡献。从计算结果中可以看出，体系的磁矩随掺杂离子浓度的增加而增大，是由于随着掺杂原子个数的增加，价带顶附近的杂质态自旋劈裂的程度增强，体系的磁矩因此增大。

3.氧空位对掺杂SnO2体系的影响

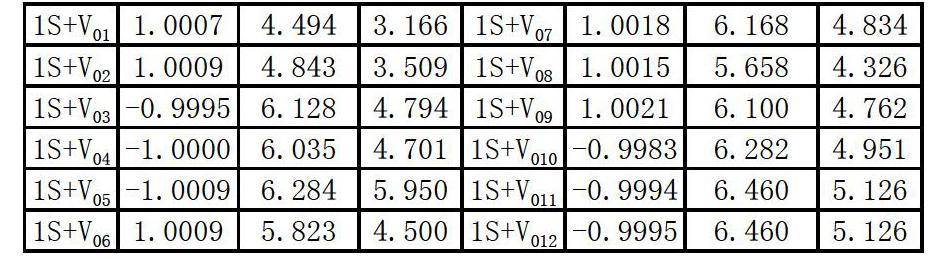
一个替代掺杂含有氧空位时，选取了12种不同的氧空位位置，如图2中蓝色球位置所示，通过体系磁性计算和形成能计算结果比较分析可知，最终选取1S+V01形成能最低的位置进行掺杂。再分析氧空位对一个替代和两个替代的掺杂体系磁性的影响。从态密度图和自旋密度图中可以看出，由于氧空位的引入，费米能级附近的杂质态自旋劈裂程度减弱，与无氧空位缺陷的体系相比，体系磁矩减小，但磁矩仍然主要由替代原子周围的O原子自旋极化产生。

三、结论

计算采用了第一性原理计算方法研究了氧空位缺陷和Li替代掺杂对SnO2体系磁性的影响，结论如下：含有氧空位的SnO2是非磁性的，而含有氧空位的Li替代掺杂SnO2体系的基态是磁性态。Li替代掺杂的SnO2体系在有无氧空位的情况下，掺杂体系为磁性态，并且体系的磁矩都随着掺杂原子浓度的增加而增大。氧空位使替代掺杂的SnO2体系的形成能降低，这表明有氧空位的情况下，替代掺杂更容易形成，这与实验结果相符合。电子结构分析表明，掺杂体系的磁矩产生主要来源于替代Li原子周围的O原子p轨道的贡献，从理论上解释了产生磁矩的原因。

【参考文献】

[1]王颖，湛永钟，许艳飞，喻正文.稀磁半导体材料的研究进展及发展前景[M].材料导报，2007，21（07）.

[2]李东，王耘波，于军等.稀磁半导体研究的最新进展 [M].功能材料，2004年增刊（35）卷.

[3]Y.S.He，J.C.Campbell，R.C.Murphy，M.F.Arendt，J.S.Swinnea.Electronical and optical characterization of Sb：SnO2[J].Mater.Res.8（1993）3131.

[4]S.Ferrere，A.Zaban，B.A.Gsegg.Dye Sensitization of Nanocrystalline Tin Oxide by Perylene Derivatives[J].J.Phys.Chem.B 101（1997） 4490.

[5]L.Z.Liu，X.L.Wu，J.Q.Xu，et al.Oxygen-vacancy and depth-dependent violet double-peak photoluminescence from ultrathin cuboid SnO2 nanocrystals[J].Appl.Phys.Lett.100，121903（2012）.

[6]S.K.Srivastava，P.Lejay，B.Barbara，S.Pailhéa，V.Madigou， and G.Bouzerar.Possible room-temperayure ferromagnetism in K-doped SnO2：X-ray diffraction and high-resolution transmission electron microscopy study[J].Phys.Rev.B 82，193203（2010）.

[7]S.K.Srivastava，P.Lejay，A.Hadj-Azzem.Non-magnetic impurity induced magnetism in Li-doped SnO2 nanoparticles[J].J.Supercond Nov Magn，2014（27）：487-492.

[8]R.G.Wyckoff，second ed.，Crystal Structures，vol.I[M].Interscience，New York，1963：239.

[9]W.Z.Wang，C.K.Xu，G.H.Wang，Y.K.Liu，C.L.Zheng.Synthesis and Raman scattering study of rutile SnO2 nanowires[J].J.Appl.Phys.92（2002）2740.

[10]刘昱，Li掺杂SnO2d0磁性的第一性原理研究[D].吉林：吉林大学，2014.

[11]肖文志.非磁性元素掺杂氧化物基稀磁半导体的第一性原理研究[D].湖南：湖南大学，2010.

[12]Gul Rahman and Naseem Ud Din.Stabilizing intrinsic defects in SnO2[J].Phys.Rev.B87，205205（2013）.

责任编辑：杨柳