某双前桥载货车转向梯形机构优化设计

王俊伟，王定华，李海波

（安徽江淮汽车股份有限公司，安徽 合肥 230601）



某双前桥载货车转向梯形机构优化设计

王俊伟，王定华，李海波

（安徽江淮汽车股份有限公司，安徽 合肥 230601）

摘 要：文章采用解析法推导了前桥内外轮之间的转角关系，并以梯形臂长m，梯形底角θ为优化变量建立优化方程，最后并应用MATLAB软件编制了“转向梯形机构优化设计”程序，对某双前桥载货车转向梯形进行了优化，优化结果显示优化效果明显，达到了设计目的。

关键词：双前桥；转向梯形；转角关系；优化

10.16638/j.cnki.1671-7988.2016.03.019

CLC NO.: U462.2 Document Code: A Article ID: 1671-7988(2016)03-57-05

引言

汽车的转向性能直接影响整车操纵稳定性和轮胎的使用寿命等，这点在双前桥载货车上表现尤为突出。双前桥载货车转向系统的设计需要优化转向系结构来实现最佳的转向过程(转向时所有转向轮都处于纯滚动状态或只有极小的滑移)，达到减小轮胎磨损、转弯半径和转向阻力矩的目的。为了避免车轮在转向过程中横向滑移，而保持纯滚动，所有车轮轴线都应交于同一点，即车轮都应绕同一瞬时中心点转动，即所谓的阿克曼理论转向特性，这时内、外车轮转角关系就是理论转角关系[1]。采用双前桥转动的汽车为满足这一要求，同一转向桥内、外车轮转角关系需要通过转向梯形来实现。由转向梯形机构实现的内、外轮转角关系就是实际转角关系[2]。如果转向梯形机构不合理，则理想转角关系与实际转角关系之间会存在着较大的误差，为了减少误差，须采用优化设计方法对转向梯形机构进行优化。

1、双前桥转向梯形优化数学模型

图1为四轴双前桥载货车向右转向时内外车轮转角关系图。

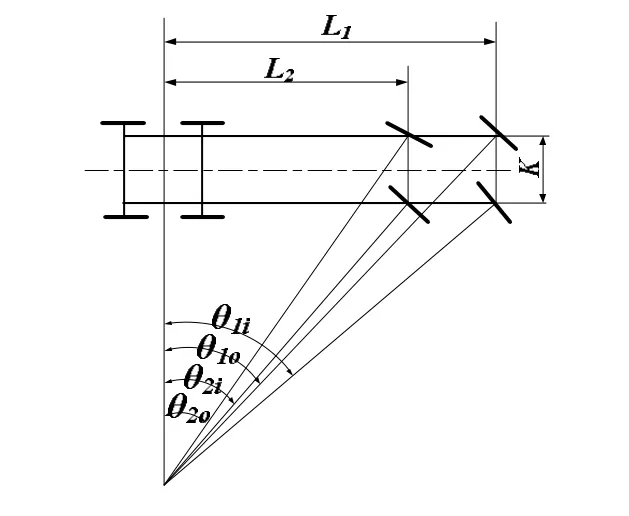
图1　双前桥转向轮转角关系图

同一转向桥内、外轮理想转角关系应满足阿克曼原理：

K---转向主销中心延长线与地面交点之间的距离；

L1、 L2---第一、二桥转向桥中心线到双后桥中心线的距离。

2、同一转向桥内、外轮实际转角关系

传统的求解转向梯形实际转角关系方案，是将汽车转向梯形简化为平面机构[3]。但实际上汽车的转向轮都具有车轮外倾角，并且转向主销又具有主销内倾角和主销后倾角（前轮前束对转向轮转角关系的影响甚微，可以忽略前轮前束的影响），所以转向梯形是个空间机构。为提高设计精度，就必须考虑汽车转向车轮定位角对梯形机构运动模型的影响[4]。

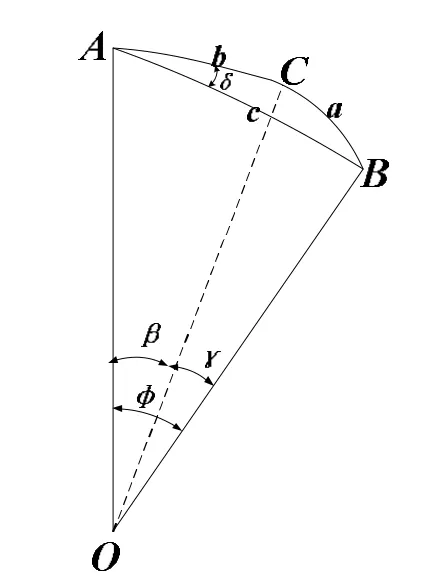
图2　左转向轮各定位角之间关系

若△ABC为球面三角形且球的半径取单位长度时，则有

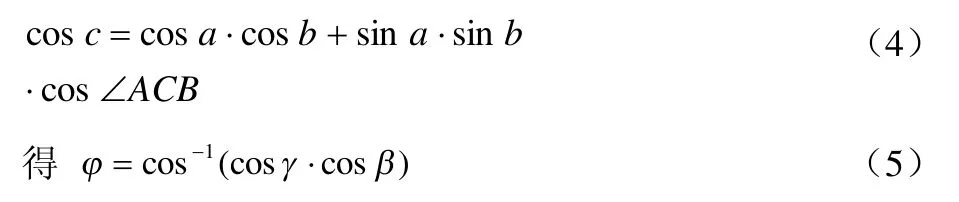
由球面三角形的正弦公式

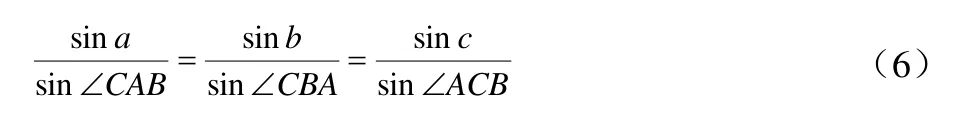
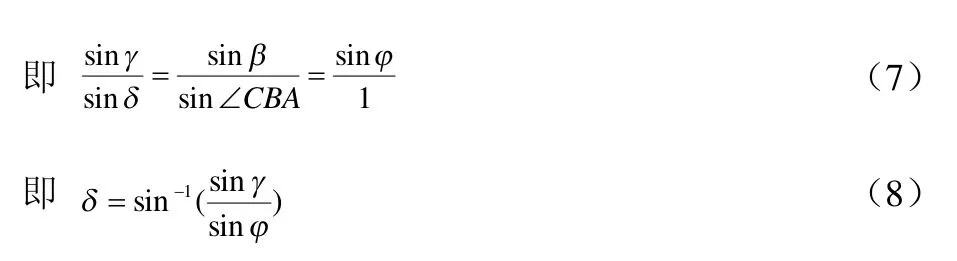
式中δ=∠CAB ，如图2所示。

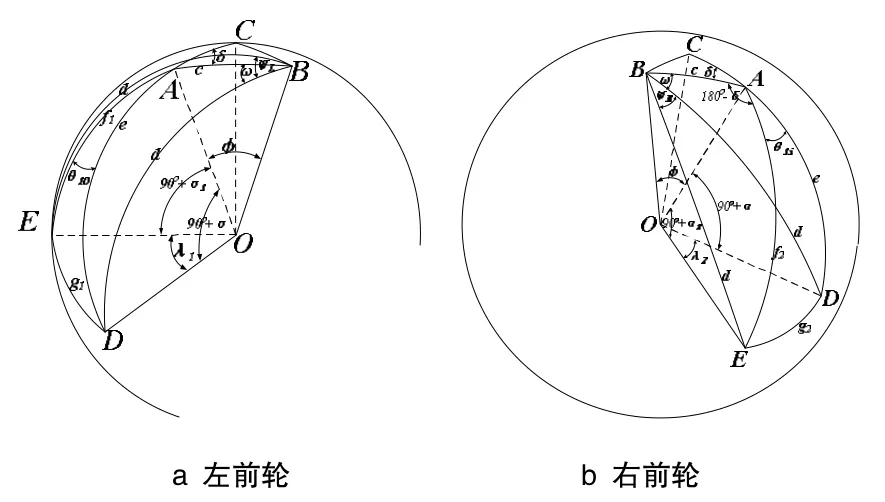
图3　汽车前轮转向主销轴线与车轮轴线之间的关系

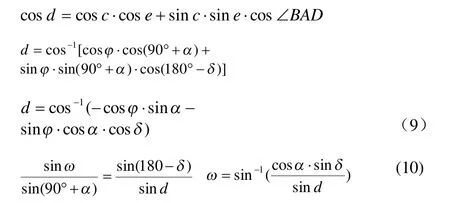
由球面三角形△BDE：

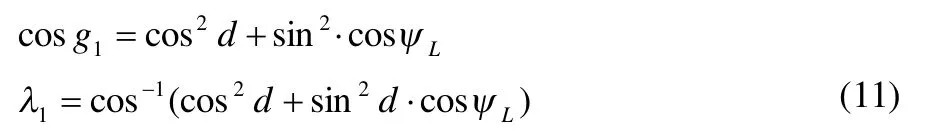
由球面三角形△ABE：

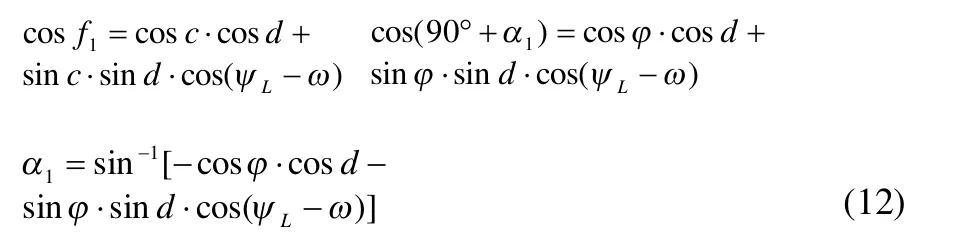
由球面三角形△ADE：

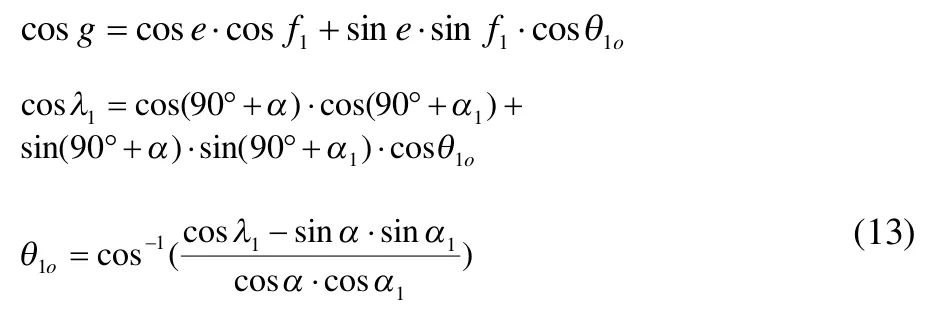
由球面三角形△ABE：

由球面三角形△BDE：

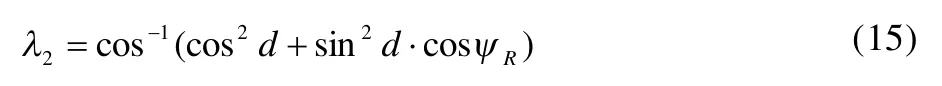
由球面三角形△ADE：

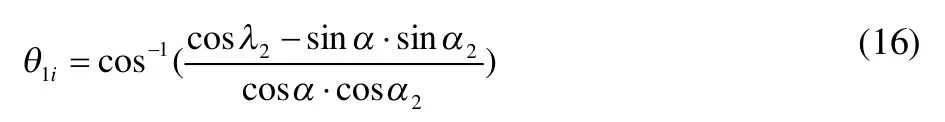
取O1，O2分别为左、右坐标系的原点；取主销轴线O1ZL，O2ZR分别为左、右坐标系的Z轴，并且当这两个轴共同绕转到包含汽车前桥轴线的铅垂面上时（这是主销只有内倾角β而无后倾角），令坐标轴XL，YL；XR，YR如图5所示。这样来建立左右坐标系时，则图4可看成是图5的两个坐标系绕转一个主销后倾角后的坐标位置。在左右坐标系中转向梯形的左右臂O1A ，O2B分别为它们的坐标平面XLYL，XRYR内，设O1A 与YL之夹角为ψ0。则与YR之夹角必为在汽车转向时，当O1A 绕主销转过ψL时，设相应地绕其主销转ψR角，则点A，B在左右坐标系中的坐标分别为：

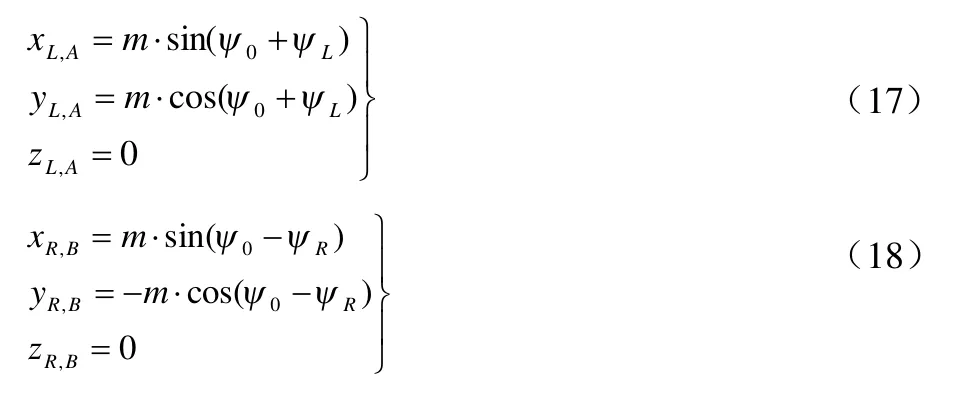
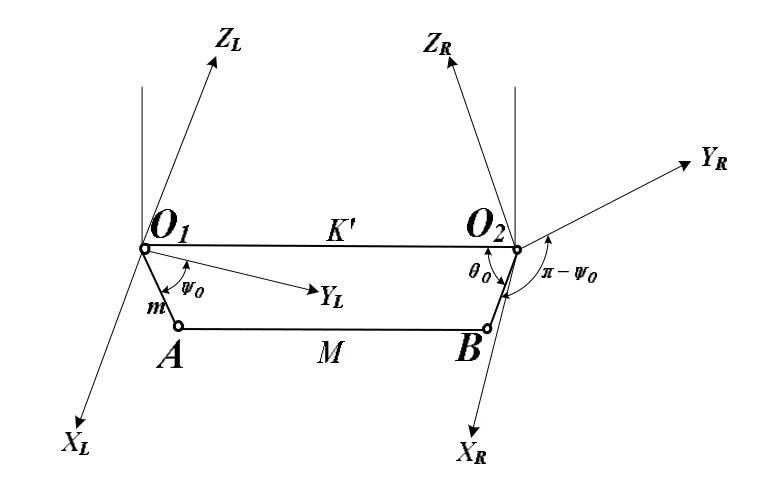
图4　转向梯形的坐标系及几何关系

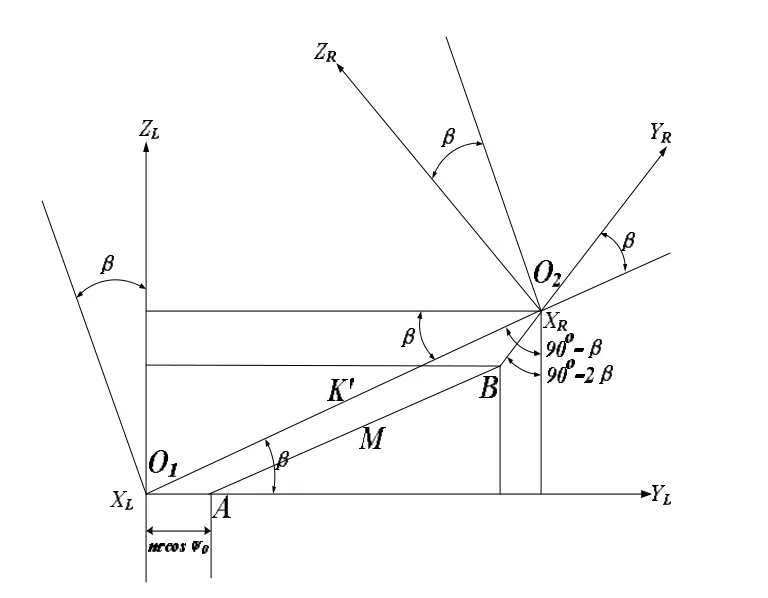
图5　转向梯形左、右坐标系坐标变换

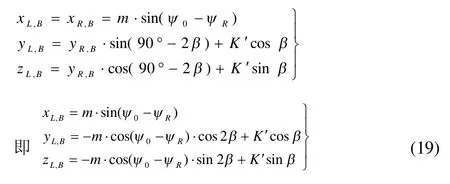
图2.6知点A，B之间的距离为：

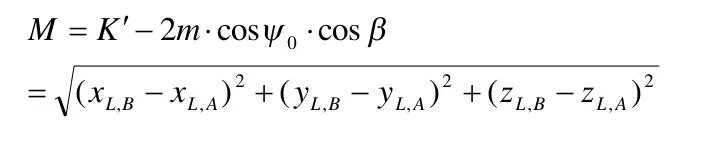
将式（17），（19）代入上式经整理后可得到：

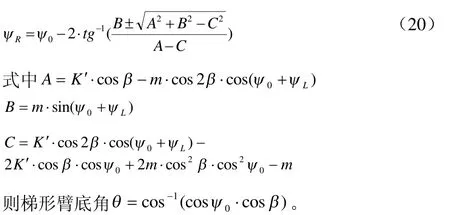
这样，与式（13），（16）有关的参数均已求出。将它们代入该两式并通过式（20）将两式联系起来，可以求得转向梯形所给出的左、右轮转角关系为：

3、前桥转向梯形优化设计

3.1 优化设计变量

影响转向轮转角关系的因素主销内倾角β，主销后倾角γ，车轮外倾角α，梯形机构的上底之长K'由汽车的总体设计确定，还需要知道梯形臂长m，梯形底角θ才能确定梯形机构，因此选取m,θ作为优化设计变量，即

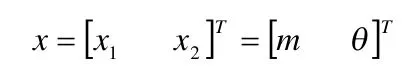
3.2 优化设计目标函数

由于转向梯形机构本身的原因，目前常用的转向梯形，不可能绝对保证在任何转角时都满足理论转向特性的要求，因此，目标函数取实际梯形特性和理想梯形特性的差值最小。在经常使用的中间位置附近小转角范围内，希望偏差尽可能小，以减小高速行驶时轮胎的磨损；在不经常使用且车速较慢的较大转角时，可适当放宽要求，因此引入加权函数ω(θO)

当θ1O在范围内变化时，每隔1°计算，将其分成40等分，来确定目标函数：

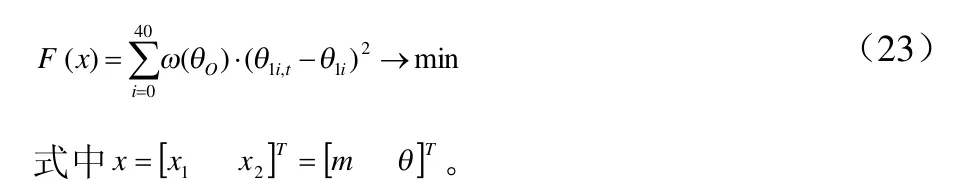
3.3 优化设计约束条件

建立约束条件时应考虑：设计变量m及θ过小都会使横拉杆上的轴向力过大；当m过大时则会引起布置困难，故对m的上下限及θ的下限设置约束条件，由于θ愈大，梯形愈接近矩形，F(x)值就愈大，而优化过程是求F(x)的极小值，故可不必对θ的上限加以限制。通常，，以此为约束：

另外，还应保证转向梯形具有足够大的传动角。所谓传动角，是指梯形臂与横拉杆所夹的锐角，它随着车轮转角增大而逐渐减小，且最小传动角总是发生在内轮一侧。传动角过小会造成有效分力过小和拉杆径向力的增加，导致转向沉重、回正不良和拉杆工况恶劣。由机械原理可知，在一般的平面连杆机构设计中，为了保证机构传动良好，四杆机构的传动角δ不宜过小，一般取但是目前设计的汽车上后置式转向梯形机构的传动角δ都偏小，这一方面是因结构所限，另一方面也是因为汽车在正常行驶中多采用中小转角转向，约有80%以上的转角在20°以内，即使是大转角转向，也是从小转角开始，而且速度较低，工况并不严重。考虑到汽车转向梯形机构不是周期、高速地传递运动，而是间歇、低速地传递运动，梯形各工作位置使用率不相等：中间位置使用率最高，极限工作位置很少使用，而最小传动角恰是发生在极限工作位置附近，在中间位置时一般都能保证传动角δ≥40°。综上，汽车转向梯形机构的最小传动角可比一般机械四杆机构的允许最小传动角小些，这里取对于每个转向梯形的传动角约束：

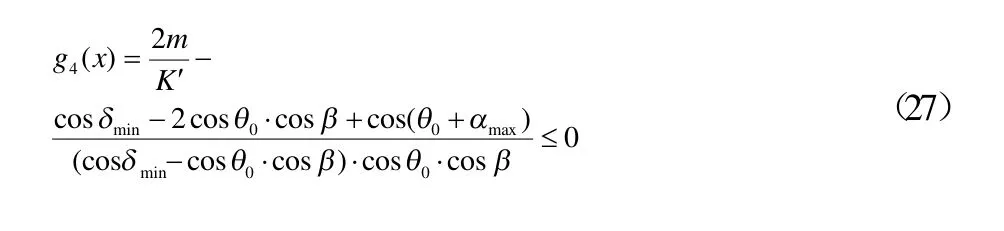
4、优化仿真实例

基于MATLAB优化工具箱中的优化计算函数来编制“转向梯形机构优化设计”程序。

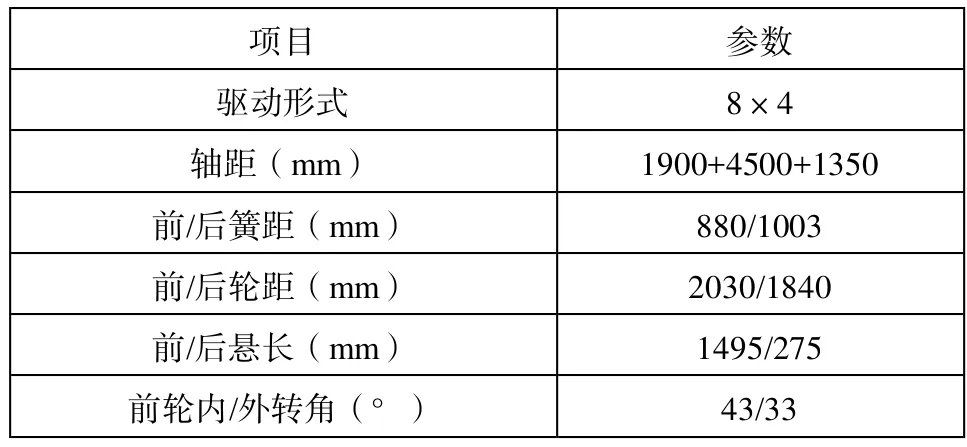
表1　整车结构参数

输入整车基本结构参数（见表1 整车结构参数）得出双前桥载货车的转向梯形进行优化设计结果（见表2和表3）。第一桥和第二桥转向梯形特性见图6和图7。

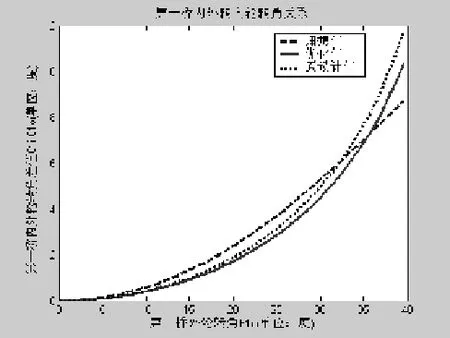
图6　第一桥转向梯形特性

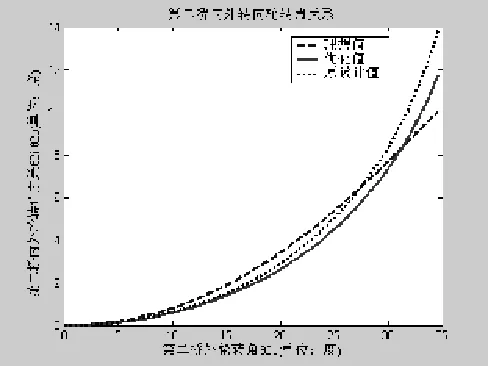
图7　第二桥转向梯形特性

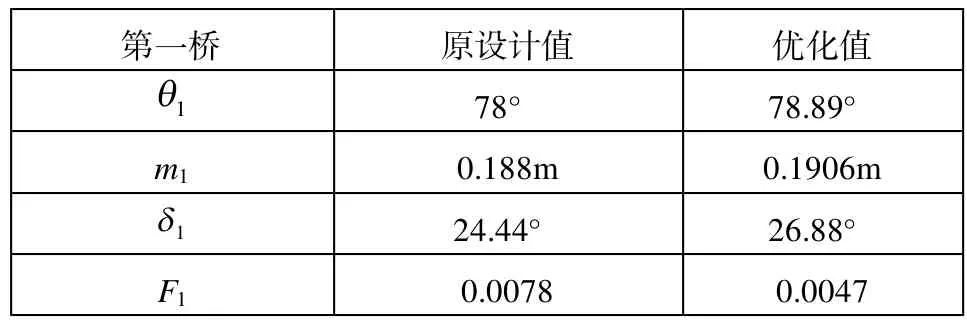
表2　第一桥参数

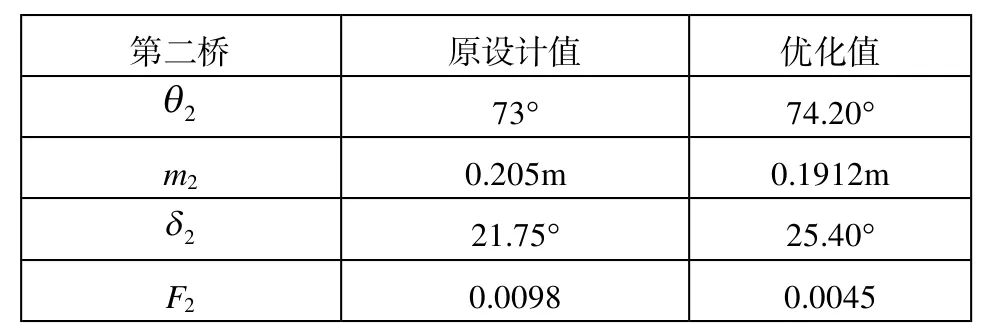
表3　第二桥参数

从上面的内外轮转角关系曲线中可以看出，经过优化后，内外轮实际转角关系与理论转角较为吻合，满足优化目标。

5、结论与分析

本文建立了汽车整体式前桥转向梯形优化模型，并编制“转向梯形机构优化设计”程序，可以较为方便的对转向梯形进行设计优化，优化效果明显，达到了设计目的。在优化设计过程中需关注以下两点：

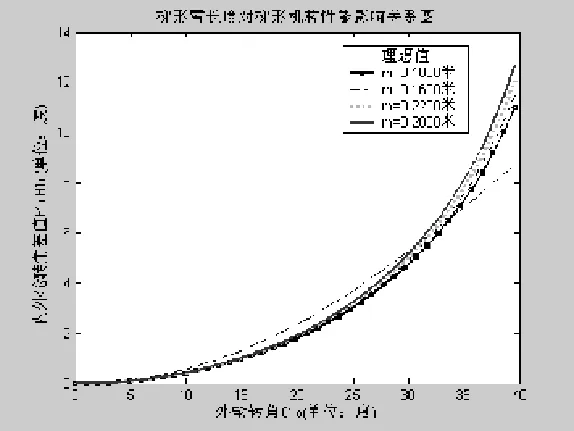
图8　梯形臂长度对梯形机构性能影响关系

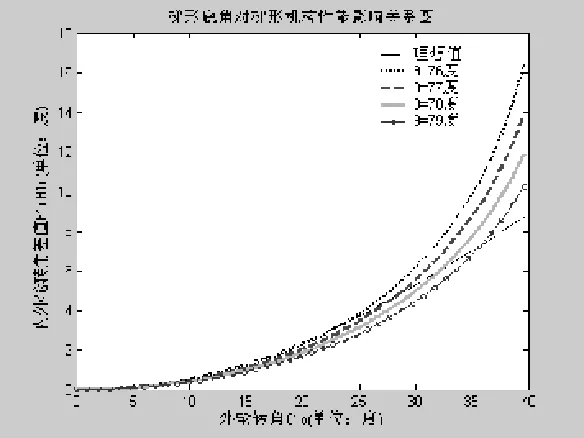
图9　梯形底角对梯形机构性能影响关系

（1）在优化设计过程中，两个优化设计变量（梯形臂长度m和梯形底角θ）对转向梯形性能影响程度不同。图8和图9分别是梯形臂长度m和梯形底角θ对转向梯形性能影响的模拟对比图。从图8中可看出：改变m对转向梯形的性能影响并不显著；从图9中可以看出：θ的变化对转向梯形性能的影响很显著，并且在一定转角范围内（在25度以内），增大梯形臂长度m和减小梯形底角θ都可以提高转向梯形的性能。但在大转角时，则有相反的趋势。这就要求在设计转向梯形机构时，应综合考虑各方面因素，根据实际工况的需要来加以选择。

（2）在优化设计过程中还发现在常用的约束范围内，减小梯形底角θ通常是受最小传动角δmin约束的限制，δmin的减小会明显的使梯形机构的误差下降，因此δmin的选择成为转向梯形设计的关键。对于优化约束中最小传动角δmin的选择，应在满足实际要求的前提下尽可能减小，以保证实际转向特性能符合阿克曼转向特性。

参考文献

[1] 余志生,汽车理论:第五版[M].北京:机械工业出版社,2009.

[2] 王望予.汽车设计：第五版[M].北京：机械工业出版社，2009.

[3] 王三民,诸文俊.机械原理与设计：第一版[M].北京：机械工业出版社,2000.

[4] 王霄锋.汽车底盘设计.北京：清华大学出版社,2010.

The Optimization Design of Steering Trapezium Frame for A double front axles truck

Wang Junwei, Wang Dinghua, Li Haibo
（Anhui Jianghuai Automobile Co., Ltd, Anhui Hefei 230601）

Abstract:In this paper, the turning angles relationship of the internal and exernal wheels in the first axle was gotten in analytic method.And the optimization equations were established by the length of steering trapezium arm m and steering trapezium cornerθ.Then the program about the optimization of steering trapezium structure was written with MATLAB and emulated for the steering trapezium of double front axle truck.The result was improved obviously after optimization.

Keywords:double front axle; steering trapezium; the relationship of turning angles; optimization

作者简介：王俊伟，就职于安徽江淮汽车股份有限公司。

中图分类号：U462.2

文献标识码：A

文章编号：1671-7988(2016)03-57-05