弹性腔流激耦合共振及声辐射机理研究
高 岩,沈 琪,俞孟萨
(中国船舶科学研究中心 a.船舶振动噪声重点实验室;b.江苏省绿色船舶技术重点实验室,江苏 无锡 214082)
弹性腔流激耦合共振及声辐射机理研究
高 岩a,b,沈 琪a,b,俞孟萨a,b
(中国船舶科学研究中心 a.船舶振动噪声重点实验室;b.江苏省绿色船舶技术重点实验室,江苏 无锡 214082)
利用Elder空腔声学模型,分析了典型空腔腔口剪切振荡和刚性壁腔体声模态的频率特征。采用模态法建立了弹性壁腔体模态声阻抗计算模型,并计算分析了腔口剪切振荡与弹性腔体耦合的归一化声辐射函数。研究表明弹性壁提供的附加压缩性,降低了空腔模态频率,增大了腔口剪切振荡与空腔模态耦合共振及强声辐射的可能性,并由试验验证了计算结果。
空腔;剪切振荡;腔体声模态;耦合共振;声辐射
0 引 言
当航速增加时,流动激励产生的振动和声辐射可能成为水下航行体的主要噪声源。流动激励产生水动力噪声机理中,大部分情况都是产生宽频带水动力噪声,其强度一般随流速的五次方增加,而当腔口剪切振荡与空腔声模态耦合时产生低频线谱声,且会随流速变化出现锁定现象。半个世纪以来,围绕流体经开口或空腔伴随发生的流激振荡和声辐射现象,进行了一系列的研究,早年 Rossiter[1]给出了空腔剪切振荡频率与孔腔驻波共振频率经验公式,Kwon[2]获得的单调音频率估算公式与试验结果吻合较好,Elder[3-5]对刚性壁空腔开展研究,分析了空腔及来流状态对开口剪切层影响,建立了腔内声压和辐射声压之间的关系,East[6]和Heller[7]通过试验测量,建立了深腔和浅腔共振频率预报的经验公式,Lafon[8]对空腔引起的剪切振荡频率进行理论与试验评估,Ronneberger[9]研究了水中空腔腔口剪切层振荡的预报方法,Kook[10]进一步提出了空腔前反馈增益函数,并结合反馈增益函数,构成了反馈回路分析框架,Marsden[11]进一步揭示了空腔深度方向声模态与剪切层振荡相互作用,引起的空腔声响应强度与来流速度和腔深有关,Burroughs[12]测量了水流经空腔产生的单调音,分析了单调音频率与流速、开口尺寸之间的关系,Meissner[13]则采用理论模型,建立了适用于空腔耦合共振的声辐射预报模型,Ashcroft[14]采用数值方法,计算了低速湍流流经二维空腔的单调音辐射噪声,远场声场分布及来流速度和边界层厚度的影响,Gloerfelt[15]采用两种不同的数值方法,计算空腔辐射噪声,Oshkai[16]针对来流充分湍流及声源远小于空腔长度的情况,研究了轴对称空腔的流动单调音及其与空腔长度的关系,Arunajatesan[17]采用数值模拟方法,计算分析了格栅肋条对剪切层振荡的影响,Dequand[18]、Tang[19]、Graf[20]等人研究了管路分支管口剪切振荡及声辐射模型和特征,Tam和Walker[21]则采用数值模拟,计算切向来流情况下窄缝共振腔附近的流动。这些研究基本都是针对刚性腔壁情况。
一般来说对于水下腔体而言,由于声波波长较长,空腔声模态频率一般远高于腔口剪切振荡频率,腔口剪切振荡频率与空腔声模态频率产生耦合的可能很小,一般不会出现较强的低频线谱噪声。但是,这里忽略了一个关键因素,就是实际空腔壁面是弹性而不是刚性的,相应的空腔模态频率受到壁面的影响,可能与腔口剪切振荡产生耦合共振。本文利用Elder[4]空腔声学模型,分析了典型空腔腔口剪切振荡和刚性壁腔体声模态的频率特征;采用模态法建立了弹性壁腔体腔口模态声阻抗计算模型,并计算分析了腔口剪切振荡与弹性腔体耦合的归一化声辐射函数。研究表明弹性壁提供的附加压缩性,降低了空腔模态频率,增大了腔口剪切振荡与空腔模态耦合共振及强声辐射的可能性,并由小型水筒模型试验验证了计算结果。
1 流激腔体声学模型

图1 流激空腔结构Fig.1 The structure of cavity induced by flow
1.1 流激腔口剪切振荡及其频率
考虑典型的腔体结构如图1所示,腔体为矩形腔,其深度为h,腔口长度为L、宽度为b。腔口上下游为刚性平板,自由来流平行于刚性平板从上游向下游流经腔口,速度为U。为方便起见,取如图1所示的坐标系,坐标原点为腔口导边中点,流动方向为x方向,与流动方向垂直的腔口宽度方向为y方向,腔体深度方向为z方向。当来流流经腔口时,流动在导边x=0处开始分离产生剪切层,由于主方向存在较大的速度梯度,剪切层的不稳定对扰动产生放大作用,使剪切层不断上下摆动,幅度不断增加,到达随边x=L附近,剪切层上下摆动击打随边,产生压力脉冲,压力脉冲以声速向上游传播反馈到导边,满足一定相位条件时,剪切层扰动形成闭合反馈环,产生剪切层自持振荡。
剪切振荡与腔口流动速度剖面有关,在给定速度剖面条件下,Michalke[22]求解剪切层涡动方程,得到剪切振荡波动的一般形式:

式中:ω为扰动波角频率,ki为扰动波空间增长因子,kr为扰动波传播波数。
由于空腔的存在,腔口除了剪切层振荡以外,还有来自于腔内的横向声扰动。因此,腔口附近总的扰动质点位移为:

式中:Va为声波产生的质点速度,第二项表示剪切层振荡产生的质点位移。
当腔口导边和随边之间形成剪切层振荡—声反馈闭环时,反馈闭环满足相位条件[23]:

将会导致腔口产生剪切层自持振荡,式中:φa为反馈声由随边到达导边的相位延迟,φL为随边反馈声源与振荡波扰动的相位差。一般情况下,φa可以忽略针对不同腔口,剪切振荡频率一般表达式[1]为:


在低Ma数情况下,腔口剪切振荡频率主要取决于腔口结构和流场条件,而与腔深无关。而且腔口剪切层自持振荡的声辐射比较弱,只有当腔口剪切层自持振荡与腔体声模态耦合时,才会产生较强的声辐射。因此,进一步考虑腔口剪切层自持振荡与腔体内声场的相互作用。
1.2 流激腔口剪切振荡与腔体声模态耦合及声辐射
当腔口流体剪切振荡频率接近腔体声模态频率时,引发耦合共振及强声辐射。此时,一方面腔口剪切振荡压力产生的腔内声响应会反馈到腔口,对剪切层产生扰动。大多数情况下,声反馈对剪切层的扰动可以忽略,但在耦合共振时,这种声反馈的影响显著增加;另外一方面,腔口剪切层振荡脉动体积速度激励空腔声模态响应。腔口剪切振荡与空腔声模态耦合共振产生的声辐射,其波长远大于腔口尺寸,可认为是点声源,远场辐射声压表示为:

式中:r为远场场点距离,ρ0为声介质密度,k0为声波数,Qc为表征声源强度的体积速度,它由两部分组成:

式中:Qa为腔口声体积速度,取决于腔口质点速度Va和腔口面积S,Qa=Va·S,对应(2)式的第一项;Qh为水动力驱动体积速度,取决于腔口的垂向速度场分布,可由腔口剪切层质点垂向位移估算,Qh=LUξh,ξh为腔口最大水动力位移,对应(2)式第二项。
Elder[3,5]认为:空腔和腔口可视为并联的共振电路,水动力体积速度Qh产生的腔口声压为:

式中:Za为腔口声阻抗,Zc为空腔声阻抗。
如果不考虑剪切层放大的耦合效应,声体积速度与腔口声压的关系为:

式中“-”表示声体积速度由内往外。联立(8)式和(9)式,有:

将(10)式代入(7)式后,再代入(6)式,则流动激励下腔口剪切层振荡和空腔声模态耦合的声辐射可表示为:

由(11)式可见,计算腔口剪切层振荡和空腔声模态耦合声辐射,除了试验测量获得剪切层振荡参数以外,还需要已知空腔及腔口声阻抗。文献[24]给出的圆柱腔腔口声辐射阻抗为:

式中:a为腔口半径,当矩形腔口边长小于3个波长时,矩形腔口声阻抗与直径等于边长的圆形腔口的声辐射阻抗接近。
对于刚性腔体,其声阻抗为:

这样,腔声阻抗为:

当腔口声抗为零时,空腔发生共振,其条件为:


联合(4)式和(16)式可知,在给定腔口尺寸和流速情况下,若要腔口剪切振荡频率与腔体声模态频率相等,相应空腔深度近似为:

低马赫数条件下刚性腔体发生剪切振荡与声模态耦合共振,要求腔体深度是一个很大的值,实际工程中满足此条件的可能性较小。
进一步考虑弹性壁面腔体,为简单起见,假设腔体侧壁为刚性边界,端板为弹性薄板,联合求解弹性薄板振动和腔内声压,可以得到腔口的模态声阻抗,详细过程参见附录A。这里,针对低频情况,仅考虑弹性平板的一阶振动模态,给出腔口零阶声阻抗:

式中:Z1为弹性平板声阻抗。
(A.15)式形式上与声阻抗传递公式一致,只是增加了因子它是由弹性平板以一阶模态振动的表面不均匀性引起的。当腔体顶板为理想刚性边界时,Z1→∞,则腔口声阻抗退化为(13)式。下文计算将表明腔体内部声介质提供了附加的压缩性,能够明显降低腔体声模态频率,增加腔体声模态频率与腔口剪切振荡频率发生耦合的可能性。
2 声腔耦合特性计算分析
选取模型计算参数为腔口长度0.2 m≦L≦0.6 m,腔体深度0.4 m≦h≦0.8 m,来流速度1 m/s≦U≦5 m/s。
2.1 剪切振荡频率特性
图2给出了腔口剪切振荡频率与来流速度、腔口长度及阶数的关系。腔口长度为0.2 m,来流速度由1 m/s增加到5 m/s,1阶剪切振荡频率从1.9 Hz增加到9.4 Hz,2阶剪切振荡频率从4.4 Hz增加到21.9 Hz,3阶剪切振荡频率从6.9 Hz增加到34.4 Hz;腔口长度为0.6 m,来流速度由1 m/s增加到5 m/s,1阶剪切振荡频率从0.6 Hz增加到3.2 Hz,2阶剪切振荡频率从1.5 Hz增加到7.3 Hz,3阶剪切振荡频率从2.3 Hz增加到11.5 Hz。可见,来流速度低于5 m/s,腔口长度0.2 m≦L≦0.6 m时,1阶、2阶和3阶剪切振荡频率分别小于10 Hz、25 Hz和35 Hz。
2.2 刚性壁腔体声模态频率特性
图3为刚性壁腔体声模态频率随腔体深度和腔口长度的变化,腔口长度为0.2 m,腔体深度由0.4 m增加到0.8 m,1阶声模态频率从773 Hz降低到424 Hz;腔口长度为0.6 m,腔口深度由0.4 m增加到0.8 m,1阶声模态频率从572 Hz降低到356 Hz。可见,在所选取的腔体参数范围内,腔体1阶模态频率远高于剪切振荡频率。

图2 剪切振荡频率与流速、腔口长度及阶数关系Fig.2 Relationship of velocity,mouth length and order with shear oscillation frequency
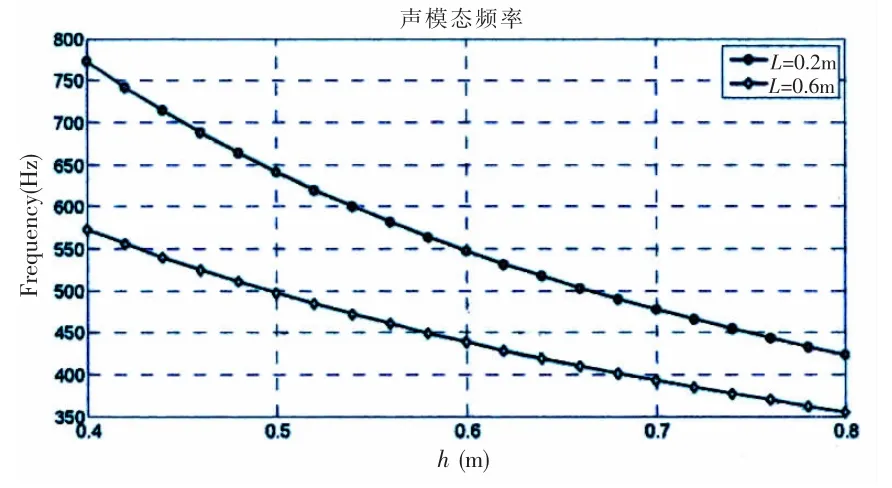
图3 刚性腔体声模态频率随腔深和腔口长度变化Fig.3 Change of rigidity modal frequency with cavity depth and mouth length
2.3 刚性壁腔体归一化声辐射函数频率特性
为进一步分析刚性壁腔体声辐射的频率特性,由(11)式定义归一化声辐射函数p/LUξh,计算得到的刚性壁腔体归一化声辐射函数随腔体深度和腔口长度变化的结果由图4给出。腔口长度为0.2 m,腔体深度由0.4 m增加到0.8 m时归一化声辐射函数峰值频率从783 Hz降低到424 Hz;腔口长度为0.6 m,腔体深度由0.4 m增加到0.8 m时归一化声辐射函数峰值频率从593 Hz降低到358 Hz。腔体深度和腔口长度增加,归一化声辐射函数峰值频率随之降低,但仍远高于腔口剪切振荡频率。因此,刚性边界条件下,腔口剪切振荡与腔体声模态不可能发生耦合共振。

图4 刚性壁腔体归一化声辐射函数随腔体深度变化(左:L=0.2 m,右:L=0.6 m)Fig.4 Change of normalization acoustic radiation function in rigid cavity with cavity depth(left:L=0.2 m,right:L=0.6 m)
2.4 弹性壁腔体归一化声辐射函数频率特性
针对弹性壁腔体,选取同样的腔体尺寸,计算分析归一化声辐射函数随腔体深度、腔口长度及弹性端板厚度的变化,结果见图5。腔口长度为0.2 m,腔深为0.6 m,端板厚度由8 mm减小到1 mm时归一化声辐射函数的峰值频率从467 Hz降低到29 Hz;腔口长度为0.6 m,腔深为0.6 m,端板厚度由8 mm减小到1 mm时归一化声辐射函数的峰值频率从64 Hz降低到2.8 Hz。结果表明弹性端板为腔内部声介质提供附加压缩性,明显降低空腔声模态频率,增加空腔声模态与腔口剪切层振荡耦合共振的可能性。文献[25]利用小型低噪声水筒,试验测量了空腔模型的声辐射特性。空腔模型腔口长320 mm,深800 mm,宽215 mm,壁板厚度为10 mm和3 mm两种。测试表明,壁板厚度10 mm时未发生剪切振荡和空腔声模态耦合共振;壁板厚度3 mm,水速4.5 m/s左右时腔口剪切振荡与空腔声模态发生耦合共振及强声辐射且随流速变化出现锁定现象,参见图6和图7,由图可见,剪切振荡频率和空腔声模态频率在5 Hz左右发生耦合共振,峰值量级增加约40 dB,其倍频也出现强声辐射。
实际情况下,水下航行体的腔体多为连通空腔,腔体结构更复杂,腔体声模态频率受弹性腔壁的影响向低频偏移更明显,腔口剪切振荡与空腔声模态应该容易发生耦合共振及强声辐射。

图5 归一化声辐射函数随弹性端板厚度变化(左:L=0.2 m,右:L=0.6 m)Fig.5 The changes of normalization acoustic radiation function with elastic end plate thickness(left:L=0.2 m,right:L=0.6 m)

图6 不同厚度腔壁腔体辐射声压随速度和频率变化(左:10 mm,右:3 mm)Fig.6 The cavity wall radiation pressure change of different thickness with flow velocity and frequency(left:10 mm,right:3 mm)

图7 3 mm壁板腔体不同速度的辐射声压(f=5 Hz,L=320 mm)Fig.7 3 mm wall cavity radiation pressure in different flow velocity(f=5 Hz,L=320 mm)
3 结 论
刚性边界条件下,腔口剪切振荡与腔体声模态不可能发生耦合共振;对弹性腔而言,弹性壁为空腔内部声介质提供附加压缩性,降低空腔声模态频率,增加空腔声模态与腔口剪切层振荡耦合共振和强声辐射的可能性;试验测试表明薄壁板空腔模型4.5 m/s左右水速下腔口剪切振荡与空腔声模态发生耦合共振及强声辐射且随流速变化出现锁定现象。
参 考 文 献:
[1]Rossiter.Wind tunnel experiments on the flow over rectangular cavities at subsonic and transonic speeds[Z].Rep.Mem. 3438,Aeronautical Reserch Council,1964.
[2]Kwon Y P.Feedback mechanism of low-speed edge tones[J].J Acoust.Soc.Am.,1998,104(4):2084-2089.
[3]Elder S A.Self-excited depth-mode resonance for a wall-mounted cavity in turbulent flow[J].J Acoust.Soc.Am.,1978,64 (3):877-890.
[4]Elder S A.Forced oscillations of separated shear layer with application to cavity flow tone effects[J].J Acoust.Soc.Am., 1980,67(3):774-781.
[5]Elder S A.Mechanism of flow-excited cavity tones at low mach number[J].J Acoust.Soc.Am.,1982,72(2):532~549.
[6]East L F.Aerodyamically induced resonance in rectangular cavities[J].J Sound and Vibration,1966,3(3):277~287.
[7]Heller H H,Holmes D G,Covert E E.Flow-induced pressure oscillation in shallow cavities[J].J of Sound and Vibration, 1971,18(4):545-553.
[8]Lafon P,Caillaud S,Devos J P,Lambert C.Aeroacoustical coupling in a ducted shallow cavity and fluid/structure effects on a steam line[J].Journal of Fluids and Structures,2003,18:695-713.
[9]Ronneberger D.The dynamics of shearing flow over a cavity-a visual study related to the acoustic impedance of small orifices[J].J of Sound and Vibration,1980,71(4):565-581.
[10]Kook H,Mongeau L.Analysis of the periodic pressure fluctuations induced flow over a cavity[J].J of Sound and Vibration, 2002,251(5):823-846.
[11]Marsden O,Bailly C.Investigation of flow features and acoustic radiation of a round cavity[J].J of Sound and Vibration, 2012,331:3521-3543.
[12]Burroughs C B,Stinebring D R.Cavity flow tones in water[J].J Acoust.Soc.Am.,1994,95(3):1256-1263.
[13]Meissner M.Self-sustained deep cavity oscillation induced by grazing flow[J].Acustica,1987,62:220-228.
[14]Ashcroft G B,Takeda K,Zhang X.A numerical investigation of the noise radiated by a turbulent flow over a cavity[J].J of Sound and Vibration,2003,265:43-60.
[15]Gloerfelt X,Bailly C,Juve D.Direct computation of the noise radiated by a subsonic cavity flow and application of integral method[J].J of Sound and Vibration,2003,266:119-146.
[16]Oshkai P,Rockwell D,Pollack M.Shallow cavity flow tones:transformation from large-to-small-scale modes[J].J of Sound and Vibration,2005,280:777-813.
[17]Arumajatesan S,Sinha N.Modeling approach for reducing Helmholtz resonance in submarine structures[R].AO-A458237, 2005.
[18]Dequand S,Hulslowff S J.Self-sustained oscillations in a closed side branch system[J].J of Sound and Vibration,2003, 265:359-386.
[19]Tang S K.On sound transmission loss across a Helmholtz resonator in a low mach number flow duct[J].J Acoust.Soc,Am., 2010,127(6):3519-3525.
[20]Graf H R,Ziada S.Excitation source of a side-branch shear layer[J].J of Sound and Vibration,2010,329:2825-2842.
[21]Tam C K W,Ju H,Walker B E.Numerical simulation of a slit resonator in a grazing flow under acoustic excitation[J].J of Sound and Vibration,2008,313:449-471.
[22]Michalke A.On spatially growing disturbances in an inviscid shear layer[J].J Fluid Mech,1965,23:521-544.
[23]张明敏,何祚镛.导流板对腔口流体自持振荡影响的研究[J].应用力学学报,1995,12(2):9-16. Zhang Mingmin,He Zhayong.The influence of the flange of cavity on the fluid dynamic self-sustained oscillations[J].China Journal of Applied Mechanics,1995,12(2):9-16.
[24]何祚镛,赵玉芳.声学理论基础[M].北京:国防工业出版社,1983.
[25]沈 琪.流激开孔和空腔模型振动噪声控制和模型试验报告[R].无锡:中国船舶科学研究中心科技报告,2015.
附 录:
A mechanism study on coupling resonance and acoustic radiation of elastic cavity induced by flow
GAO Yana,b,SHEN Qia,b,YÜ Meng-saa,b
(a.National Key Laboratory on Ship Vibration&Noise;b.Jiangsu Key Laboratory of Green Ship Technology, China Ship Scientific Research Center,Wuxi 214082,China)
The frequency characteristics of shear oscillation and the rigid wall acoustic modal about typical cavity are investigated by Elder cavity acoustic model.Modal method is adopted to establish modal acoustic impedance calculation model about the elastic wall cavity,and normalization acoustic radiation function is calculated and analyzed on shear oscillation and coupled elastic wall acoustic modal.Studies show that the elastic wall could provide additional compressibility to reduce the cavity modal frequencies and increase the possibility of coupling resonance and strong acoustic radiation,and the calculation results are validated by experimental results.
cavity;shear oscillation;cavity acoustic mode;coupling resonance;acoustic radiation


TB53
A
10.3969/j.issn.1007-7294.2016.08.013
1007-7294(2016)08-1036-09
2016-06-01
高 岩(1982-),女,工程师,E-mail:44187420@qq.com;沈 琪(1988-),男,助理工程师;俞孟萨(1960-),男,研究员。

