两层流中潜体运动与诱发内波特征关系研究

丁 勇，段 菲，韩盼盼，牛明昌

（哈尔滨工程大学 船舶工程学院，哈尔滨 150001）

两层流中潜体运动与诱发内波特征关系研究

丁 勇，段 菲，韩盼盼，牛明昌

（哈尔滨工程大学 船舶工程学院，哈尔滨 150001）

在两层流体中潜体运动会激发生成内波。文章通过编程控制潜体运动，使用动态分层法保证潜体运动时边界层不受影响，基于RANS方程多相流模型，采用求解相的体积分数方式捕捉内界面波形。潜体定常运动计算结果与实验结果相符，通过此方法，对比不同潜深下潜体诱发内波波高和波长随密度Froude数的变化特征，得到了诱发内波波高最大处的临界密度Froude数，重点研究了在临界密度Froude数处潜体加速运动和减速运动对诱发内波幅值及其波动过程的影响。

两层流体；潜体尾迹；非定常运动；内波

0 引 言

水下航行体在分层流体中运动时，其周围水质点受到体积效应下的浮力作用，在约化重力作用下，分层界面附近流场将产生波动从而形成了内波。在源生内波的研究中，两层流体模型受到人们的格外关注。在无粘假设下，Lu等[1-2]采用稳定相方法给出了点源运动产生的内界面波形解，Yeung[3]和Wei[4]等通过Green函数法探讨了点源运动诱生的内波模式与表面波模式对内界面兴波的影响，Xu等[5]运用线性理论研究了含密越层的三层流体中卵形体产生的内波速度梯度场，Zhu等[6]采用边界元理论方法以求解球体在上层流体运动的内波波形；Gourlay[7]以及Fritts[8]等采用直接模拟法研究了粘流场中漩涡对源生内波的影响，Chernykh[9]采用RANS下的数值模拟方法模拟了分层流中有净动量的自航尾迹。目前绝大多数研究以潜体定常运动状态为研究对象，以相对运动法来模拟潜体在分层流中的运动。

本文将通过编程控制潜体的绝对运动，运用动态分层法保证潜体运动时边界层不受影响，确保此处有更稳定的y+值以提高计算精度，基于RANS方程多相流模型，采用CFD技术，重点研究潜体加速和减速运动对内波幅值及其波动过程的影响。通过与实验值对比定常运动结果，确定本文模拟方法的可行性，对比分析不同潜深下潜体定常运动诱发内波波高、波长随密度Froude数的变化特征，得到诱发内波波高最大处的临界密度Froude数；在临界密度Froude数处的运动速度下，定义加速度无量纲数，研究潜体加速和减速运动对内波幅值及其波动过程的影响，进一步定量讨论加速度和减速度的大小与内波幅值的关系。

1 数值计算方法与模型

在两层流体中求解非稳态的连续方程和Navier-Stokes方程时，假设两种液体互不相溶，以q流体为例，引入体积分数变量αq，两层流体交界面通过求解q流体相的体积分数连续性方程（1）得到：

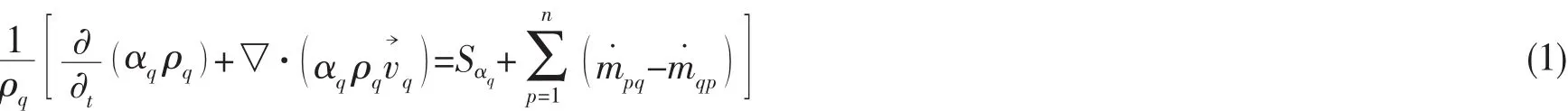
对于主相，它的体积分数由（2）式约束计算得到。

体积分数方程通过显式时间的离散来求解，采用当前时刻之前的时间步长带入标准有限差分插值方案中进行体积分数值的计算。

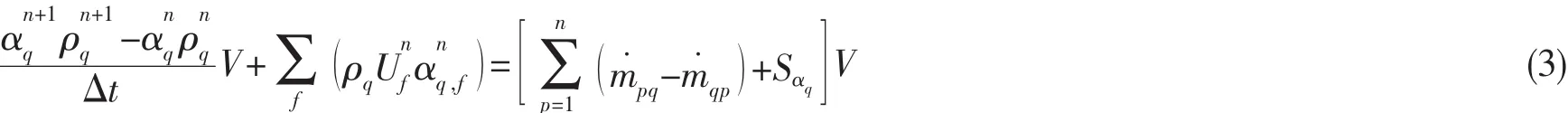
其中：n+1代表当前的时间步长；n代表前一间隔的时间步长；αq，f是通过一阶迎风格式计算得到的q流体体积分数在表面处的值；V为计算单元的体积；Uf是根据正常速度流体在表面处的体积通量。

由于表面力使用散度定理可以表示为体积力，而这个体积力正是添加给动量方程的源项，此模型采用Brackbill等[10]提出的连续表面力模型。当一个单元中只有两相时，体积力为：

其中：σij为表面张力系数，为表面曲率，。

本文通过编程控制潜体运动规律，运用动态分层法保证潜体运动时边界层不受影响，确保此处有更稳定的y+值，通过理想高度和分割因子（合并因子）两种参数来控制这一过程。（5）式表示当网格被拉伸大于一定高度时，该层网格会分裂为两层网格，（6）式表示当网格被压缩小于一定高度时，该层网格会与相邻的另一层网格相融合变为一层网格。

其中：h是网格高度，hideal是理想高度，αs是分割因子，αc是合并因子。

为了使用这种方法，需要对计算域进行变形。在潜体运动方向分割出一个条形内域，内域随着潜体的水平运动进行平动，其他部分为外域，内域与外域之间以interface相连，这样内域在平动时会引起周围网格的生成与消去，但不会对外域的网格造成影响。图1为计算模型示意图。

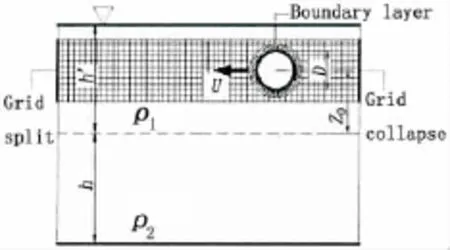
图1 计算模型示意图Fig.1 Sketch of the calculation model

在计算中取h′=0.15 m，h=0.25 m，潜体直径D=0.05 m，ρ1= 998.2 kg/m3，μ1=1.003×10-3kg/（m·s ），ρ2=1 023.79 kg/m3，μ2= 0.981 1×10-3kg/（m·s）。

在密度分层的流体中潜体运动会诱发生成内波，内波特征取决于密度Froude数Frd。

其中：U为潜体运动速度，Δρ为两层流体密度差，h′为上层流体厚度、h为下层流体厚度。

2 潜体匀速运动对内波波高及波长的影响

潜体匀速运动诱发内波特征计算结果将与Arntsen[11]在分层水槽中的实验结果进行对比。图2所示即为本文方法计算得到的潜体位于内界面之上1.6D、Frd=0.6时的波形图，内波波高值取前两个波中的最大值，波长值取最大波高处对应的波长。本文重点考察潜体运动速度以及潜深的变化对内波波形的影响，因此密度Froude数中的变量仅改变运动速度，考察范围为0.2＜Frd＜1.0，潜深的影响分别考察潜体位于内界面之上2.3D、1.6D、1.0D以及位于内界面之下0.9D、1.4D的情况。图3为内波波高随Frd变化的对比结果，波长变化结果见图4。

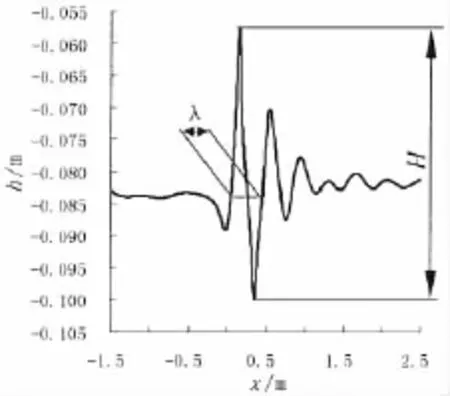
图2 Z0/D=1.6，Frd=0.6时内波波形图Fig.2 Internal wave at Z0/D=1.6,Frd=0.6

在本文考察的所有计算范围内，数值计算结果与实验结果吻合良好，确定通过编程和动态分层法模拟分层流中潜体运动的可行性。结果显示，内波波高与波长随密度Froude数的变化趋势与潜深无关。内波波高值随运动速度的增加先增大后减小，在Frd≈0.6波高最大，在0.2＜Frd＜1.0的范围内，波高值减小幅度对比增大幅度较小；潜体潜深仅改变幅值大小，潜体运动距离内界面越近，诱发内波幅值越大，而当Frd＞0.8时，潜体位于内界面之下距离1.4D诱发的内波幅值比0.9D的幅值大。

内波波长的度量以上层流体高度h′为参考，随着潜体运动速度的增加波长值呈指数形式增大，在0.2＜Frd＜1.0的的范围内，最大波长值发生在Frd=1.0处，当潜体在上层流体中运动时，潜体距离内界面越近，相同速度下诱发生成的内波波长越小，而当潜体在下层流体中运动时，结果相反；与实验结果相比，本文由于假设两种液体没有相互穿插，密越层厚度几乎为0，而实验中由于淡水与盐水的相容性，存在一定厚度的密越层，约为圆柱直径的0.7～1.0倍，因此与实验结果存在一定偏差，但是本文计算方法有效地解决了由于水池长度的限制Frd＞0.8时产生的内波未达到有效的稳定状态，波长无法获得的缺陷，以及内波波高太小难以测量等问题。

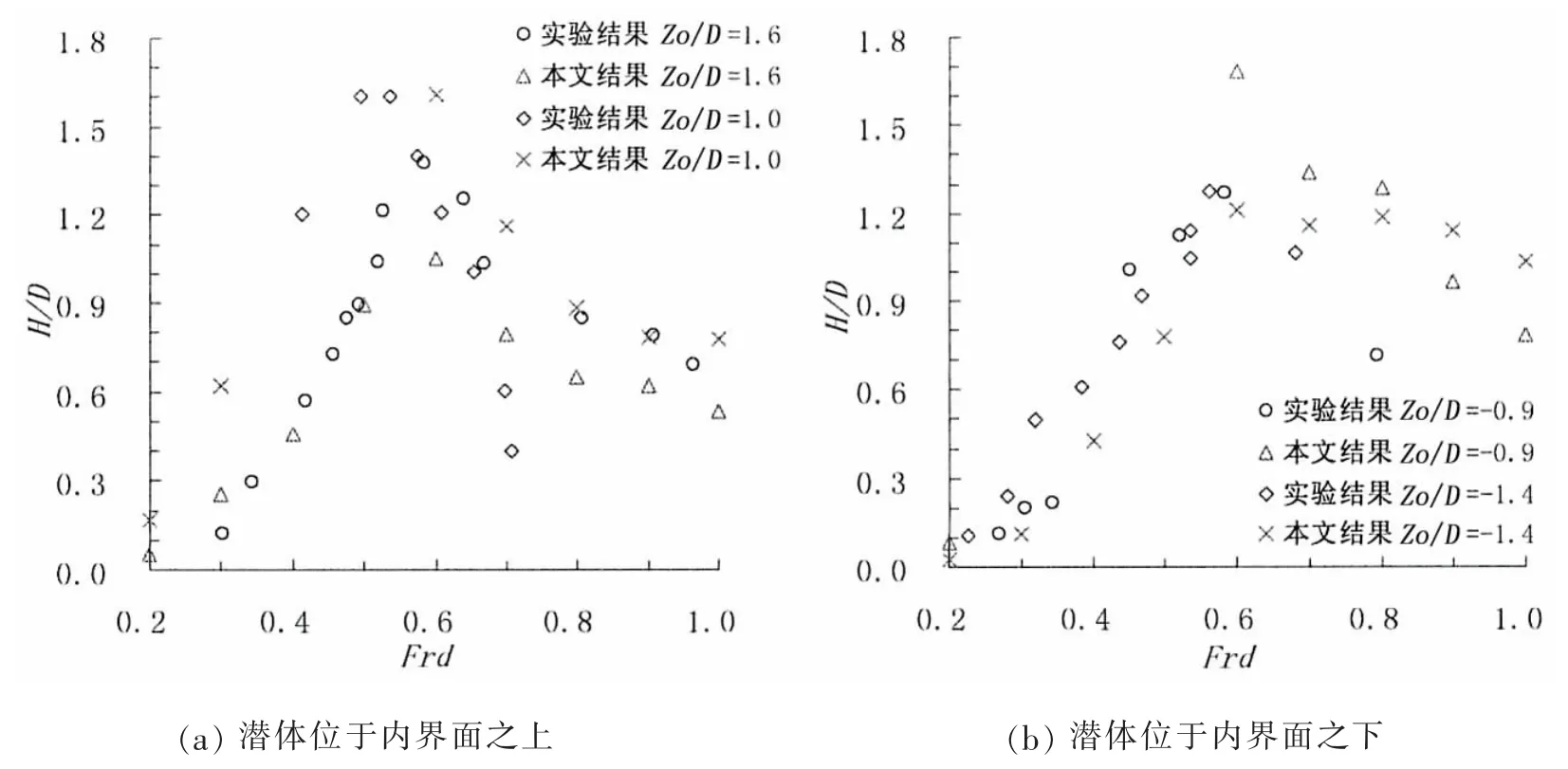
图3 不同潜深下内波波高（H/D）随Frd变化Fig.3 Variation in internal wave heights(H/D)with Frdat different depth

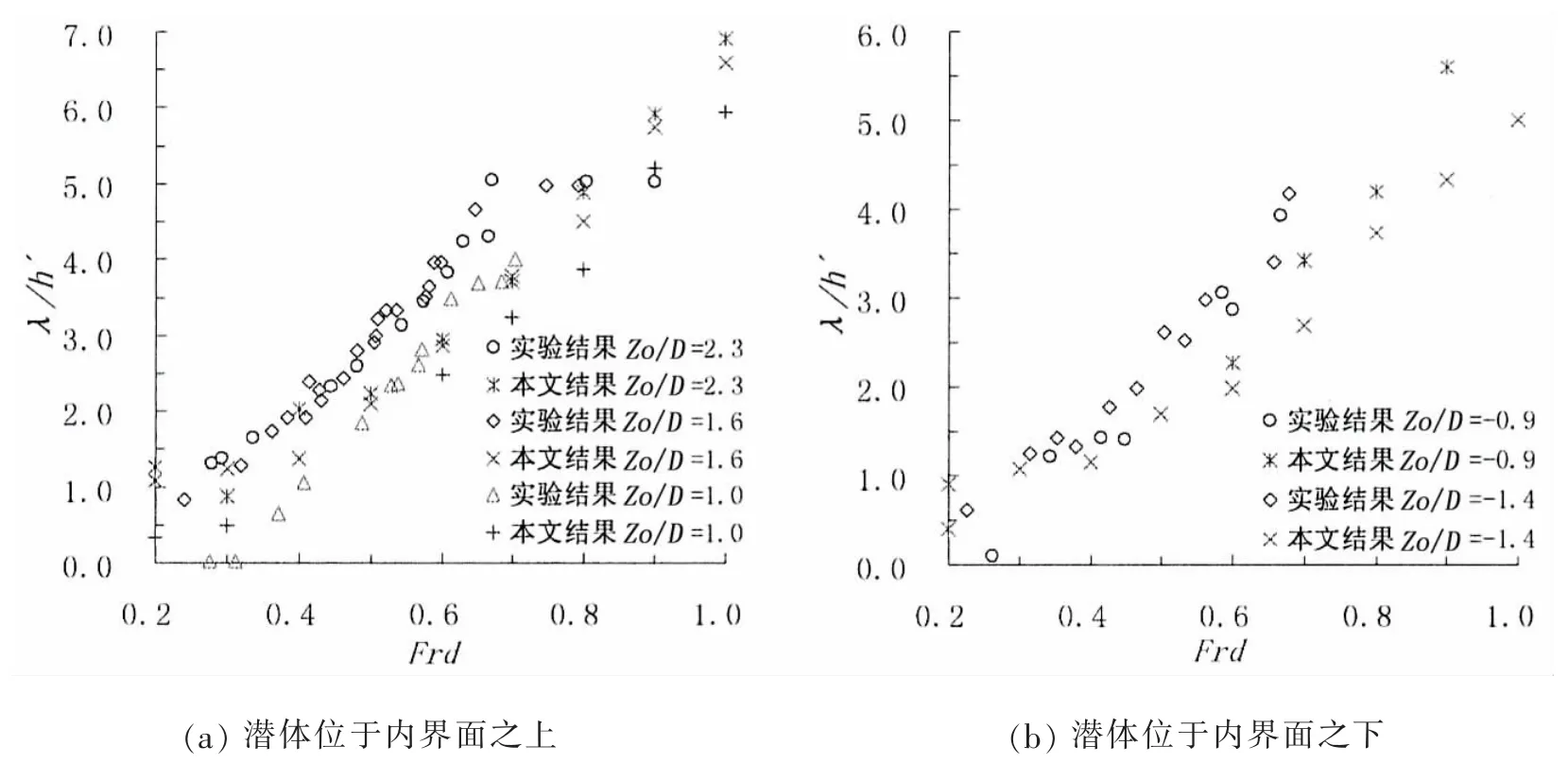
图4 不同潜深下内波波高（λ/h′）随Frd变化Fig.4 Variation in internal wave heights(λ/h′)with Frdat different depth

3 潜体加/减速运动对内波波幅的影响

本文重点研究潜体非定常运动时诱发内波幅值与波动过程特征，定义描述加速度无量纲数为，其中a为潜体运动加速度，υ=μ/ρ为流体运动粘性系数。潜体匀速运动结果显示，在各个潜深处当Frd≈0.6时内波波高最大，因此当潜体位于内界面之上2.3D处以Frd=0.6匀速运动并达到稳定状态时，分别研究潜体以Ara=±0.908 5×103、Ara=±1.112 7×103、Ara=±1.573 6×103作加速运动和减速运动诱发内波幅值与波动过程。

定义在运动潜体正下方诱发的内波第一波峰称之为“First Hump”，内波第一波谷称之为“First Valley”也称之为首波峰及首波谷，第二个波峰称之为“Second Hump”，波谷称之为“Second Valley”也称之为次波峰及次波谷。

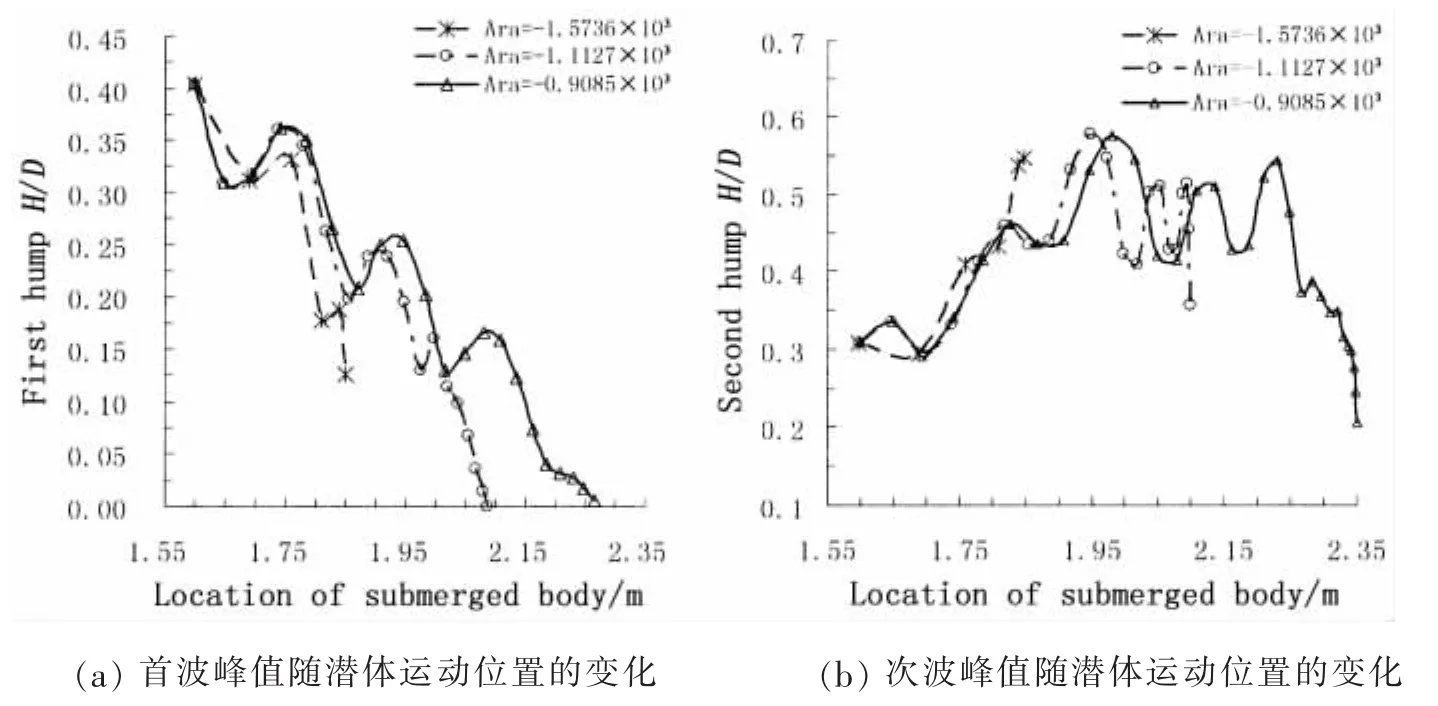
图5 潜体减速运动诱发生成内波的峰值变化Fig.5 Peak-curves of internal wave induced by submerged body deceleration motion

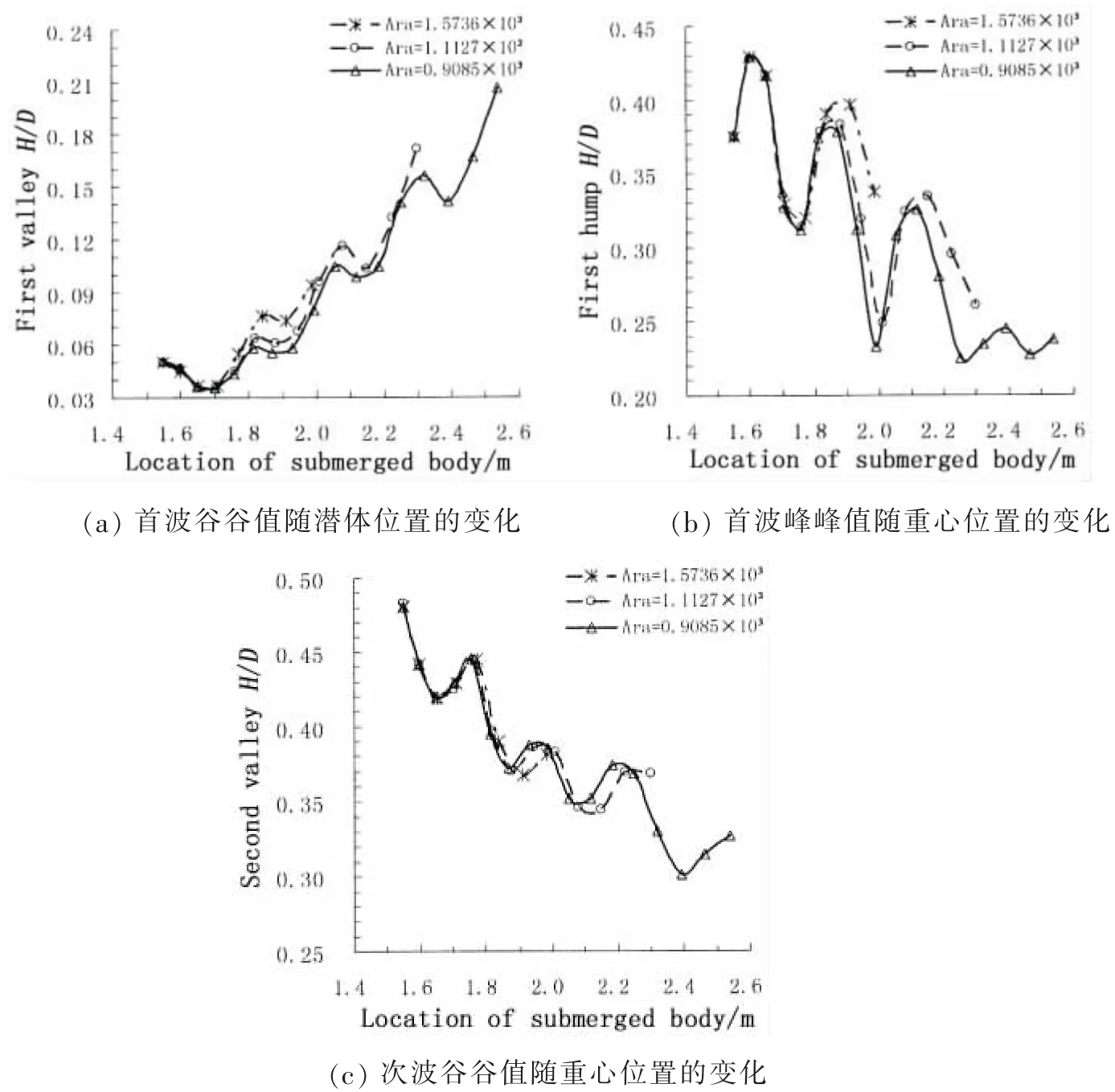
图6 潜体做加速运动诱发生成内波的峰值变化Fig.6 Peak-curves of internal wave induced by submerged body acceleration motion

图5为不同减速度下潜体减速运动过程中内波峰值变化曲线，每隔0.5 s取一次值，可以看出内波峰值都是呈波动性的变化。处于潜体正下方的首波峰峰值随潜体速度减小H/D从0.41迅速衰减，当潜体速度减为0时，以减速度Ara=-1.573 6×103运动导致的内波首波峰值H/D减小到约0.12，显然此时潜体虽静止但首波峰还未完全衰减，而当减速度为Ara=-0.908 5×103和Ara=-1.112 7×103时，速度减小接近0时首波峰几乎为0；次波峰的变化伴随着减速的开始逐渐变大，H/D从0.3变化到0.6，波动幅度几乎增大了一倍，以增大后的幅度波动性地持续一段时间后迅速衰减，从图5（b）可看出几乎持续了三个波动周期，对比不同的减速度，当潜体速度减为0时，次波峰峰值随减速度大小依次为0.55、0.35和0.20，减速度为Ara=-1.573 6×103时，次波峰持续增大，并未衰减。

图6为不同加速度下潜体加速运动过程中内波峰值变化曲线，当Frd=1.0时完成加速运动，加速运动诱发生成的内波峰谷值依旧呈波动性变化，首波谷随潜体运动速度的增加H/D最大从0.05增大到0.21，但是相应的加速度最小为Ara=0.908 5×103，以最大加速度运动的潜体在完成加速运动时H/D仅从0.05增大到约0.10，首波峰与次波谷的变化趋势与首波谷截然相反，均随运动速度增加而减小，在加速度为Ara=1.573 6×103时潜体运动对首波峰影响不大，H/D仅从0.37减小到0.34，次波谷谷值从0.48减小到0.38，在最小加速度下，首波峰与次波谷衰减最明显，加速完成时分别减小到0.23和0.33。

4 结 论

本文基于RANS方程多相流模型，采用CFD技术，通过编程和动态分层法模拟潜体真实运动，确保在模拟过程中边界层不受影响，通过与实验值对比定常运动计算结果，确定本文模拟方法的可行性。对比分析不同潜深下潜体定常运动诱发内波波高、波长随密度Froude数的变化特征，进一步讨论了潜体加速和减速运动对内波幅值及其波动过程的影响，具体结论如下：

（1）本文计算方法可有效地模拟潜体运动诱发内波实验，并且解决了由于水池长度的限制当潜体运动速度过大内波波长无法获得的缺陷，以及内波波高太小难以测量等问题。

（2）潜体匀速运动诱发内波结果显示，在0.2＜Frd＜1.0的范围内，内波波高值先增大后减小，在Frd≈0.6时波高最大，不同潜深下潜体距离内界面越近，内波波高越大；潜体匀速运动诱发内波波长呈指数形式增大，潜体在上层流体中运动时，距离内界面越近，诱发生成的内波波长越小，而当潜体在下层流体中运动时，结果相反。

（3）潜体加速运动和减速运动过程中内波呈现波动性变化，潜体正下方的内波波幅变化趋势与速度变化相同，即加速运动时首波峰（谷）值增大，减速运动时首波峰（谷）值减小，此外，潜体加/减速度越小，运动完成时峰谷幅值变化越大。

（4）当潜体从诱发内波最大的速度处（即Frd≈0.6）开始减速时，次波峰先增大后减小，加速时，首波峰以及次波谷均呈波动性减小。

[1]Lu D Q,Chen T.Surface and interfacial gravity waves induced by an impulsive disturbance in a two-layer inviscid fluid [J].Journal of Hydrodynamics,Ser.B,2009,21(1)：26-33.

[2]Lu D Q,Chwang A T.Interfacial waves due to a singularity in a system of two semi-infinite fluids[J].Physics of Fluids (1994-present),2005,17(10)：102-107.

[3]Yeung R W N.Waves generated by a moving source in a two-layer ocean of finite depth[J].Journal of Engineering Mathematics,1999,35(1)：85-107.

[4]Gang Wei,Jiachun L,Shiqiang D.Surface effects of internal wave generated by a moving source in a two-layer fluid of finite depth[J].Applied Mathematics and Mechanics,2003,24(9)：1025-1040.

[5]Xu Z,Chen X,Sturova I V.Surface characters of internal waves generated by Rankine ovoid[J].Acta Mechanica Sinica, 2006,22(5)：417-423.

[6]Zhu W,You Y X,Miao G,et al.Waves generated by a 3 D moving body in a two-layer fluid of finite depth[J].Journal of Hydrodynamics,Series B,2005,17(1)：92-101.

[7]Gourlay M J W J F D.Direct numerical simulations of initially turbulent wakes[Z].Biloxi,MS：200118.

[8]Fritts D,Gourlay M,Orlando W,et al.Numerical simulation of late wakes in stratified and sheared flows[Z].2003：206-210.

[9]Chernykh G G,Moshkin N P,Fomina A V.Dynamics of turbulent wake with small excess momentum in stratified media [J].Communications in Nonlinear Science and Numerical Simulation,2009,14(4)：1307-1323.

[10]Brackbill J U,D.Kothe B,Zemach C.A continuum method for modeling surface tension[J].J Comput.Phys.,1992,100：335-354.

[11]Arntsen Ø A.Disturbances,lift and drag forces due to the translation of a horizontal circular cylinder in stratified water [J].Experiments in Fluids,1996,21(5)：387-400.

Research on the relationship between moving patterns of submerged body and the features of induced internal waves in two layer fluid

DING Yong,DUAN Fei,HAN Pan-pan,NIU Ming-chang
(College of Shipbuilding Engineering,Harbin Engineering University,Harbin 150001,China)

The motion of submerged body in stratified fluids will excite the generation of internal waves.In this paper,by control the motion of submerged body using user defined files,using layering to ensure the boundary layer will not be influenced by the motion of submerged body.The waveform of interface was captured by means of solving the volume fraction of each fluids based on multiphase flow model of RANS equation.The calculation results of uniform motion were in good agreement with experimental results.Comparing the the characteristics of variation in internal wave heights and lengths with densimetric Froude number at different depth the critical densimetric Froude number induced the maximum internal wave heights was obtained by this method.The interaction of submerged body acceleration and deceleration motion with induced internal wave at critical densimetric Froude number was mainly studied.

two layer fluid;submerged body wake;unsteady motion;internal wave

U661.1

：Adoi：10.3969/j.issn.1007-7294.2016.05.002

1007-7294（2016）05-0523-07

2016-01-03

装备预研专项基金资助项目

丁 勇（1959-），男，博士，教授，E-mail：dingyong@hrbeu.edu.cn；段 菲（1990-），女，硕士研究生。