两种风险度量方法的研究

李之好，周海林

(安徽财经大学 金融学院，安徽 蚌埠　233030)



两种风险度量方法的研究

李之好，周海林

(安徽财经大学 金融学院，安徽 蚌埠233030)

摘要：针对股票市场Value-at-Risk (VaR)和Expected Shortfall(ES)预测问题，选取了我国上证综合指数和深证成分指数以及创业板的收益率数据，通过历史模拟法和GARCH-Delta-Normal法对比分析，发现历史模拟法所计算出的VaR和ES与其模拟数据长度有显著关系，同时GARCH-Delta-Normal在ES的估计上优于历史模拟法而在VaR的估计上效果不好，原因是正态分布假定和GARCH模型都不能完全消除股票收益率的肥尾效应。

关键词：在险值；条件在险值；历史模拟法；Delta-Normal；后验测试

0引言

Value-at-Risk (VaR)是一种有别于传统金融风险管理的新型风险管理工具，目前得到了业界的普遍使用，同时被巴塞尔委员会用来作为银行业内部控制、资本充足率的监管指标。但是由于VAR还存在着很大的缺点，如：不能度量尾部风险，模型依赖，置信水平依赖等，因此当前对VaR的研究主要集中在模型创新和后验测试方法的开发，其次引进Expected Shortfall作为补充。[1]VaR的估计方法可分为两大类：参数法和非参数法；其中参数法严重地依赖于风险损失分布的假设，非参数法则要求大量的样本数据。历史模拟法是针对历史样本数据的非参数法，[2]蒙特卡洛模拟是针对未来样本的非参数法。而预测能力的检验方法则没有统一的标准。

在现有对VaR研究的文献中，大都专注于某一种方法的改进，对于不同方法的对比，以及同一种模型在不同市场之间的预测效力的比较缺乏探索，同时对于历史模拟法的历史样本长度和置信水平的选择的研究不是很多。因此，本文选取我国股票市场的三大股票指数为研究对象，探究历史模拟法样本长度和置信水平的选择，以及Delta-Normal和历史模拟法的预测能力的比较，同时观察VaR和ES性质差异，[3]其中上证指数和深证指数只选取(2000-2015)的样本数据，创业板则选取自上市以来的所有数据。

1VaR和ES

VaR只能刻画一定显著性水平下损失发生的最小值，无法对尾部极端值进行准确刻画，而ES正是在这一点上作为VAR的补充，专门测量在显著性水平内的平均损失，所以VaR和ES搭配使用是当前实务界普遍采用的风险管理方式。

1.1VAR(Value-at-Risk)的定义。

VaR:P{rt≤-VARt(r)|Ft-1}=1-α

其中rt是t日的收益率，α为显著性水平，Ft-1为已知信息。VAR本质是收益分布的下尾部分位点。

1.2 ES(Expected shortfall)的定义。

其中f(r)为收益率的分布函数，ES是对超过VaR损失的部分进行加权平均，分母项是尾部概率，分子项是尾部损失均值。

2VAR和ES的计算方法

2.1历史模拟法。

历史模拟法假设历史上发生的情况会再现，[4]那么对未来VAR的预测，只需要对过去样本的所用情况进行分类，找出符合VaR和ES定义的值即可。在历史模拟法中关键是确定历史样本的长度和显著性水平，因为样本长度选择不当会导致VAR受异常值的影响。历史模拟法的步骤为：

Step1:选取样本长度，确定显著性水平，计算VAR应该所在位置；

Step2:对样本数值进行排序，根据显著性水平，找出VaR值；

Step3:对超过VaR值的损失数据加权平均得出ES。

不过历史模拟法也分很多种，本文采用的是等权重的历史模拟法，这种方法的计算过程相对简单。

2.2Delta-Normal。

Delta-Normal是基于样本数列服从椭圆分布假设计算VaR和ES，在椭圆分布情况下，VaR值是和波动率成线性关系的，也就是说只需要确定了股票收益率的波动率就能算出VaR；理论研究中通常认为股票收益率服从正态分布，且简单的Delta-Normal法还要求每日的股票收益率是独立同分布的，那么我们可以得出VaR值的计算公式[5]：

Delta-Normal:VaRt(p)=z1-α×σ(r)×pt-1

其中zα是标准正态分布的1-α分位点，pt-1为t-1日的收盘价，σ(r)为股票收益率的波动率，在这里我们假定它是个静态的值。

在这里已知收益率服从N～(0,σ2)正态分布，所以Expected Shortfall如下：

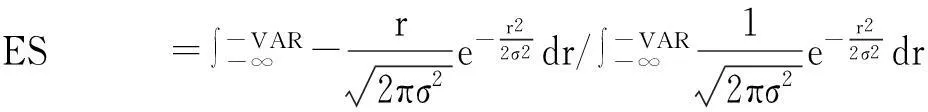
ES =∫-VAR-∞-r2πσ2e-r22σ2dr/∫-VAR-∞12πσ2e-r22σ2dr

2.3基于GARCH模型的Delta-Normal法。

2.2中静态波动率的假设与实际相差太大，现实情况现实股市波动率呈现聚集效应，因此我们用GARCH模型对波动率建模[6]，假设股票收益率服从独立异方差的正态分布，那么VAR的计算公式可以为：

GARCH-Delta-Normal:VARt(p)=z1-α×σt-1(r)×pt-1

其中pt-1为t-1日的收盘价，σt(r)为股票收益率在t时刻的动态波动率，γ为股票收益率的长期波动率。同理ES的计算也只需要将静态波动率转换为动态即可。

3预测能力检验

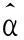
LRα=-2ln⎣(1-α)T-NαN」+2ln⎣(1-(N/T))T-N(N/T)N」

4实证分析

4.1数据处理。

对于上证指数和深证指数，由于其历史数据比较长，并且两者数据数量也基本一致，可用来做样本长度测试，分别选取过去为300、500、700样本长度作为VaR和ES的估计基础，选择不同的置信水平95%，97%和99%，能够用来减少误差；在建立GARCH模型之前首先要对股票价格进行一阶对数差分rt=ln(pt)-ln(pt-1)，检查收益率序列的平稳性，然后再进行ARCH-LM检验，发现股票指数收益率序列存在显著的异方差性，随后建立GARCH模。

4.2结果分析

4.2.1历史模拟长度影响。

如Table1所示，当历史模拟数据的区间为300和500时，VaR的估计值都通过了检验，但ES的估计值都不能通过检验；而当历史模拟数据拉长为700时，VaR作为风险指标已经失去了作用，这时的ES表现打败了VaR。说明对于上证综指和深证成指来说，运用历史模拟法进行风险度量时，在样本数据不是很充足的情况下采用VaR进行风险管理要比ES要好，当样本数据很充分的时候ES的收敛效果优于VaR；造成这种情况的主要原因是当样本数据较小时ES的计算具有很大的随意性，且一般多为极端值，很容易偏离真正的风险值，当样本数据足够大时，由于股票收益率尖峰后尾性质，VaR对于捕捉尾部损失缺乏效力。另外，从不同置信水平的LR统计量的结果来看，置信水平越高LR统计量就越小，说明对于历史模拟法来说，一定要保证置信水平足够高。

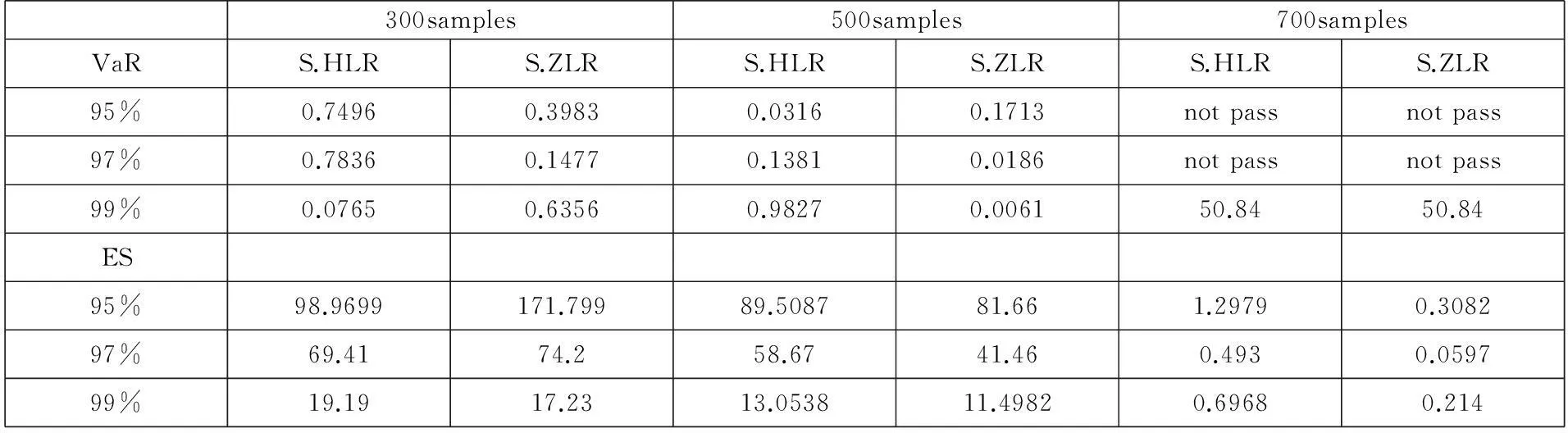
Table1　历史模拟法模拟样本的影响

4.2.2 GARCH-Delta-Normal与历史模拟法的比较。

我们分别对上证综指、深证成指和创业板指数建立GARCH模型，为了保证模型的有效性和可比性，我们都采用GARCH(1,1)模型对以上三者收益率的波动率建模，Table2中显示参数的估计值都通过T检验，且GARCH项和

ARCH项系数之和小于1，说明模型是正确的。

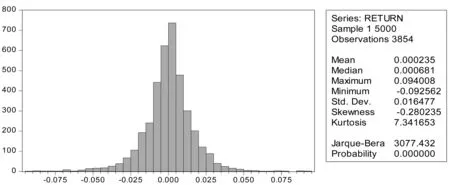
Figure1　上证指数收益率

CoefficientWARCHGARCHP1P2P3AICBICS.HGARCH(1,1)2.99E-060.0760.915000-5.626-5.619S.ZGARCH(1,1)3.98E-060.0740.915000-5.388-5.381C.YBGARCH(1,1)4.79E-060.0460.9430.02900-4.982-4.966

接着我们根据GARCH模型所估计出来的时变波动率结合2.3中的计算公式，求出VAR和ES的每日估计值。同样我们用LR似然率来检验所求结果，Table3给出了分别采用历史模拟法和GARCH-Delta-Normal的预测效果，对于Value-at-Risk的模拟，这两种方法都是适合的，但是同样我们用LR似然率来检验所求结果，Table3给出了分别采用历史模拟法和GARCH-Delta-Normal的预测效果，对于Value-at-Risk的模拟，这两种方法都是适合的，但是历史模拟法的效果要优于GARCH-Delta-Normal；而Expected Shortfall的计算，显然两种方法的效果都是很好，但是在99%的置信水平下GARCH-Delta-Normal还是能通过检验的。这说明了股票收益率有很严重的尖峰厚尾效应，我们知道波动率聚集是尖峰厚尾的一个原因，但是在这里我们已经包含了时变波动率效应，说明除了波动率聚集之外，正态分布的假设也不太符合实际，从Figure1中我们也能观察到上证指数收益率得峰度为7.34，是正态分布的两倍多。 不过也有可能需要高阶的GARCH模型。但总的来说GARCH-Delta-Normal法对于模型假设的依赖是其最大的缺点，而历史模拟法虽然看起来计算比较粗糙，除了认为历史会重演外，不受任何假设的限制，具有很大的灵活性。

Table3　两种方法结果对比

5结论

通过上面的研究，我们发现，无论是大样本还是小样本，无论是历史模拟法还是Delta-Normal将VaR和ES联合起来使用基本能够准确地进行风险度量。不过在不同的情况下VaR和ES、历史模拟和Delta-Normal效果也大不相同。在样本数据较少时，历史模拟法的VaR就足够了，而对于样本数据丰富可得，则适用历史模拟法计算ES；同时运用Delta-Normal不仅要考虑时变的波动率，还要考虑收益率真实的分布情况，在收益率峰度较大时采用高置信水平和条件VaR，反之采用95%置信水平的VAR即可。但是本文只采取了等权重的历史模拟法，其次还有加权历史模拟法、Bootstrap等，[8]现实的金融机构可以根据自身的风险管理的要求以及监管条件自动选取合适的风险度量法。

参考文献

[1]赵晓玲 陈雪蓉，周勇.金融风暴中基于非参数估计VaR和ES方法的风险度量[J].数理统计与管理，2012(3)：381-387.

[2]David E. Allen, Abhay K. Singh, Robert J. Powell. EVT and tail-risk modelling: Evidence from market indices and volatility series [J].North American Journal of Economics,2013,26(2):355-369.

[3]李芒环.金融风险管理方法VaR、ES和ES的比较[J].统计与决策，2015(8).

[4]甘霖.基于新时期沪深300指数的历史模拟法VaR风险度量[J].区域经济研究， 2014(3).

[5]John C Hull. Options Futures and Other Derivatives[M].8th edition. New York ：Pearson Education Inc,2012:524-525.

[6]Ruey S.Tsay Analysis of Financial Time Series [M].3rd edition BeiJing： Posts﹠Telecom Press, 2012.

[7]Theo Berger. Forecasting value-at-risk using time varying copulas and EVT return distributions[J].International Economics，2013(4):93-106.

[8]黄剑.历史模拟法诸模型的比较研究[J].金融研究，2010(11)：180-187.

Class No.:F832.5Document Mark：A

(责任编辑：宋瑞斌)

Study of Two Methods of Risk Measurement

Li ZhiHao, Zhou HaiLin

(School of Finance, Anhui University of Finance & Economics, Bengbu, Anhui 233030，China)

Abstract：In this paper, China's Shanghai Composite Index and Shenzhen Component Index and GEM index were selected to forecast VaR and Expected Shortfall. By comparing GARCH-Delta-Normal and historical simulation method, the results showed that the Value-at-Risk and Expected Shortfall calculated by historical simulation have a significant relationship with the lengths of samples, which is employed to forecast current VAR and ES. At the same time, GARCH-Delta-Normal in ES estimation is superior to the historical simulation method and is not good in the estimates of VAR. The reason is that normal distribution assumptions and GARCH model cannot eliminate all the effect of fat tail.

Key words：value-at-risk; expected shortfall; historical simulation; GARCH-Delta-Normal; back testing

中图分类号：F832.5

文献标识码：A

文章编号：1672-6758(2016)04-0083-4

作者简介：李之好，学生，安徽财经大学金融学院。研究方向：金融工程。

周海林，教授，安徽财经大学金融学院。研究方向：风险管理和资产定价。