基于参数辨识的时栅转台在线自动标定系统*

张天恒，李志明，杨继森（1.重庆理工大学机械检测技术与装备教育部工程研究中心，重庆400054；2.重庆理工大学时栅传感及先进检测技术重庆市重点实验室，重庆400054）



基于参数辨识的时栅转台在线自动标定系统*

张天恒1，2*，李志明1，2，杨继森1，2
（1.重庆理工大学机械检测技术与装备教育部工程研究中心，重庆400054；2.重庆理工大学时栅传感及先进检测技术重庆市重点实验室，重庆400054）

摘要：提出一种在线自动检测时栅转台误差、辨识误差模型系数和误差补偿的方法。该系统由高精度的基准量仪圆光栅、微控制器与上位机组成。在对极点8个待定参数和对极内20个待定参数分别进行傅立叶变换的参数辨识，得到辨识误差模型的系数，实现了实时在线误差补偿。为了检验在线自动标定效果，利用光电自准直仪与基于参数辨识的在线自动标定系统进行对比实验。实验结果表明，采用傅立叶变换的参数辨识，提高了时栅转台标定精度与标定效率，时栅转台的精度达到2.8″。

关键词：时栅转台；自动标定；误差补偿；参数辨识

项目来源：国家自然科学基金项目（51205434，51405049，51406020）；国家科技部重大科学仪器设备开发专项项目（2013YQ220893）

转台广泛应用于航空、航天、兵器、航海、工业等领域。时栅转台就是将时栅传感器作为转台的测角元件，时栅传感器是依据时空坐标转换理论［1-2］，基于“时间量来测量空间位移”的原创思想发明的新型位移传感器［3-4］，随着与哈量合作将时栅传感器向产业化推进中，急需解决传感器标定的关键问题。目前以高精度的仪器作为基准进行比对标定，大量应用于工业现场，如正多面棱体和多齿分度台角分度误差的互检［5］，需要多次转位实现标定，多次转位测量的可操作性较差；多传感器联合标定［6］，必须满足多传感器的坐标能够快速转换，才能实现数据的正确融合；平行双关节坐标测量机的标定［7］，采用全误差分析技术，需要设计专用的检测装置，完成特定项误差的检测工作；光电跟踪转台的标定［8］，角位移传感器的自标定［9］等，日本国家计量研究院（NMIJ）提出的等分平均法［10］，在度盘上整周均匀放置多个读数头来分离度盘刻线误差，但这种方法要求读数头读取刻线误差的一致性极高。

本文结合时栅转台中时栅角位移传感器的多对极、多读数头和每个对极内的误差规律重复性好的特点，提出了参数辨识的在线自动标定方法。设计了主副控制器的双闭环硬件结构和上位机的快速傅立叶变换（FFT）算法，对对极点与对极内误差进行参数辨识，通过主控器实现了对时栅转台在线自动标定。最后利用光电自准直仪进行精度对比实验，实验结果表明，参数辨识的在线自动标定时栅转台的精度为2.8″。该方法实现了时栅转台的高精度在线自动标定，提高了标定的效率。

1　自动标定系统

1.1基于参数辨识的硬件电路结构

为了满足低功耗/智能化的设计要求，片上系统选用数字信号处理器（DSP）和现场可编程门阵列（FPGA），副控制器选用NXP公司的高性能32位嵌入式ARM微控制器LPC2138［10］，整个电路结构如图1所示。

图1　硬件设计电路

时栅转台的信号由三相互差120°激励电源提供，经过整形，滤波。放大后变成方波信号提供给参数辨识模块。参数辨识模块由片上系统和并口转串口芯片共同完成。FPGA主要完成时栅转台与圆光栅角度的测量，DSP主要完成参数辨识的数据处理，并口转串口主要完成与上位机的通信，在上位机中通过测试软件进行较为复杂快速傅立叶运算，将得到的在线标定参数通过DSP存储在Flash中，进行误差的在线修正与补偿。

时栅转台自动定位闭环控制系统主要由副控制器构成，包括步进电机驱动、触摸屏、液晶屏驱动。I/O 口3.3 V的电源由MC33269T3.3低压差芯片提供，为了提高系统的抗干扰能力，采用TLP521高速光电隔离器进行隔离，步进电机的驱动采用PWM进行驱动。键盘驱动芯片采用带I2C接口的MAX6954AA扫描管理34个按键。存储器模块采用带I2C接口的EEPROM芯片24AA256，容量达到256 kbyte，满足系统存储要求［11］。LCD驱动模块选用74LS245。

1.2在线标定系统的软件设计

在线标定系统软件需要上位机与下位机协调运行，上位机采用VC编写，软件有较强的容错能力，有良好的可视化界面、能实时显示与存储曲线、易于操作等特点，是实现在线标定的指挥中心。主要进行快速傅立叶变换（FFT）等复杂数据的运算及标定的自动化工作。下位机主要完成时栅转台智能化的数据处理工作。系统在线标定软件的流程图如图2所示。

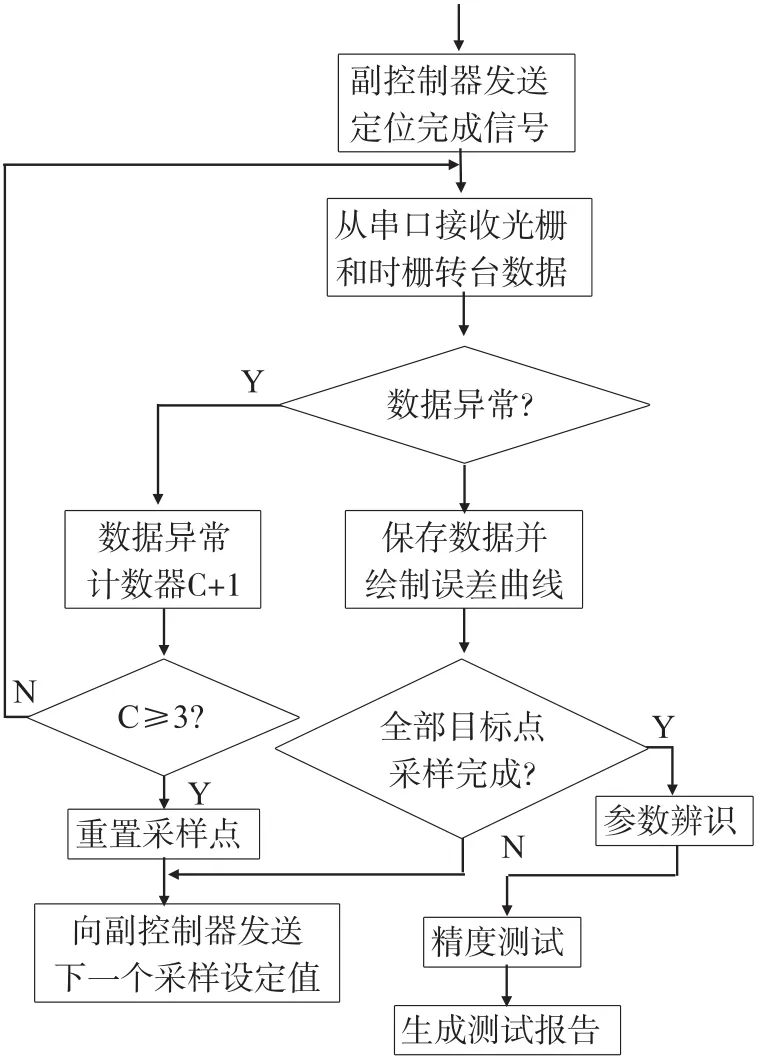
图2　自动标定系统软件流程图

2　补偿参数辨识

傅立叶变换是信号分析技术广泛应用在故障诊断、图像处理等领域［12］。在时栅转台在线标定中，误差分布曲线可用式（1）来表示：

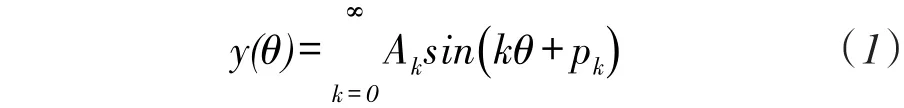
式中，y(θ)表示误差函数，Ak是第k次谐波幅值参数，单位为角秒（″），Pk是第k次谐波相位参数，单位为度（°）。

对极点采样数等于对极数，对极内采样180个点。本文应用傅立叶变换对时栅传感器的在线标定结果进行分析，得到了对极点和对极内的参数辨识，为简化数学模型，在对极点误差曲线可用式（2）表示：

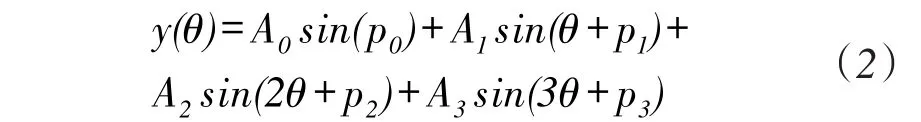
对极内误差分布曲线可用式（3）来表示：

由式（2）、式（3）利用采集的实验数据就可以计算出对极点8个待定参数，对极内20个待定参数，就可以确定时栅转台的补偿模型，实现实时的在线补偿与修正。表1是对极点的补偿参数辨识，表2是对极内的补偿参数辨识。

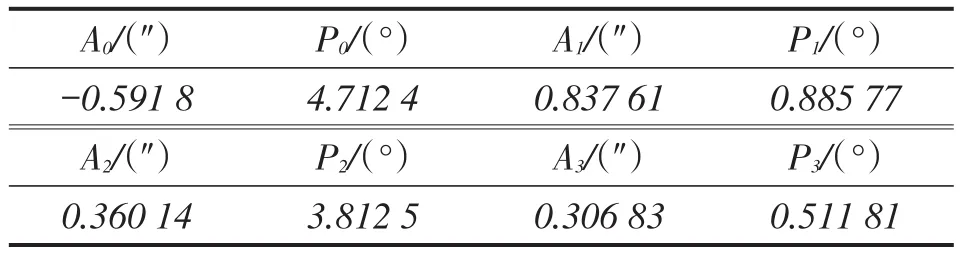
表1　对极点的补偿参数辨识

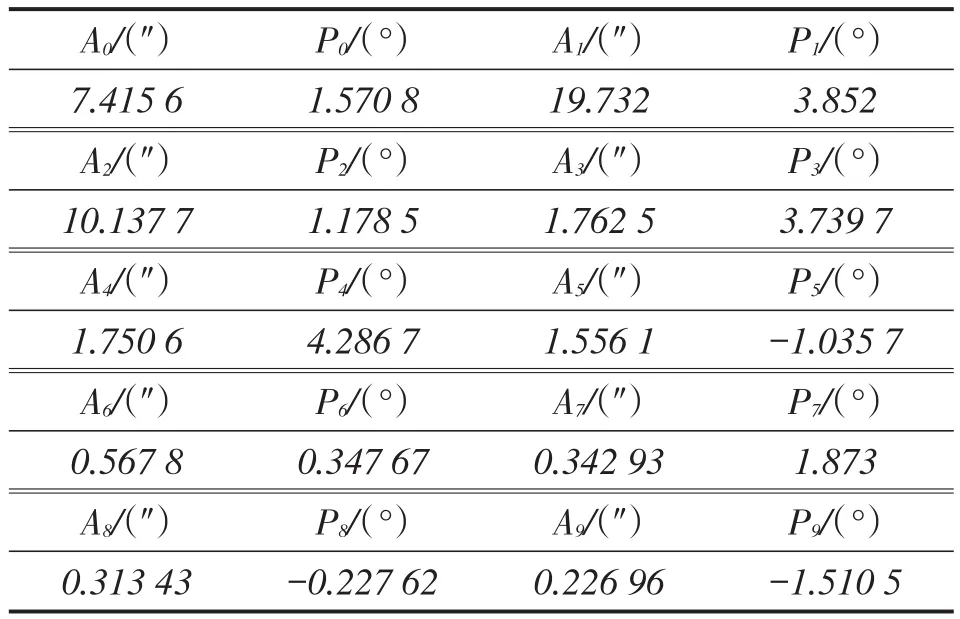
表2　对极内的补偿参数辨识

3　实验与结果

3.1在线自动标定实验系统

时栅转台在线自动标定系统实验装置如图3所示。实验台以变形量较小的大理石为基体，时栅转台固定在大理石基体上，光栅固定在载物台上。步进电机通过同步带轮跟时栅转台相连，步进电机由副控制器（数控电气箱）控制。时栅转台与光栅通过芯轴连接在一起，光栅经过200倍的细分盒IBV660B细分后接在主控制器光栅信号输入口，主控制器按一定的周期通过串口向上位机发送光栅与时栅转台的数据，从而实现时栅转台在线自动标定的整周定点数据采样。

图3　时栅转台在线标定系统实物图

3.2读数稳定性实验

时栅转台读数稳定性是影响在线标定的主要因素。打开上位机的采样，在步进电机不运动的情况下，连续采样时栅转台的数据，来测量时栅转台的读数稳定性，如果读数稳定性超过上位机设置的极限偏差，在线自动标定就没法进行。时栅转台读数稳定性如图4所示。

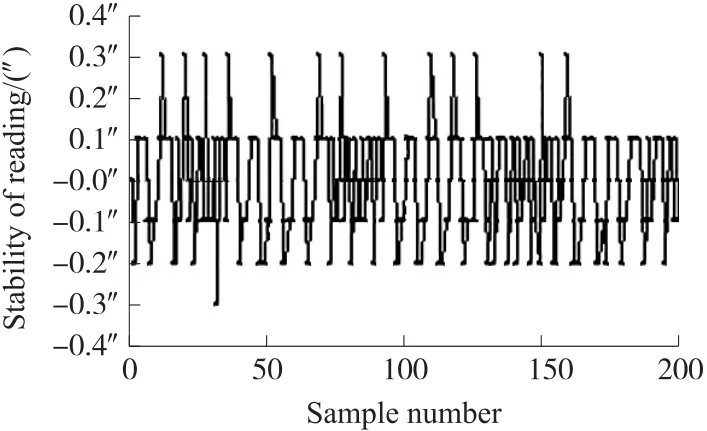
图4　时栅转台读数稳定性

3.3在线标定实验

上位机负责对采样数据进行实时参数辨识，并将辨识参数下载到主控制器中，进行误差修正与补偿。在整周进行测量，横坐标代表0°～360°整周内进行数据的采样，纵坐标代表误差的幅值，单位为（″），实测误差曲线如图5所示，补偿前的误差为142″，补偿后的误差为2.8″，如图6所示。

图5　补偿前实测误差曲线

图6　补偿后实测误差曲线

3.4比对实验

为了检验基于参数辨识的在线自动标定效果，用光电自准直仪对时栅转台进行立式与卧式比对试验，卧式比对试验系统如图7所示。

图7　光电自准直仪比对试验

图8　时栅转台与光电自准直仪比对后误差曲线

从表3可以看出，时栅转台卧式方向比对检测，时栅转台的误差为3.8″，从表4可以看出，时栅转台立式方向比对检测，时栅转台的误差为3.4″。采用参数辨识的时栅转台在线自动标定时栅转台的误差为2.8″，参数辨识的时栅转台的精度与比对试验精度还要高。

表3　卧式方向比对检测

表4　立式方向比对检测

4　结论

通过上述分析，可以解决以下3个问题：

①工作量问题。一个圆周有1 296 000″，如果分辨率为1″，采用逐点修正就要进行上百万次采样和修正；如果分辨率为0.1″，就要进行上千万次采样和修正［14］。而采用本方法提高了工作效率。

②零点问题。如果采用逐点修正法，上百万个孤立点相互之间没有任何规律可遵循，这时时栅转台空间位置的绝对零点尤为重要，一旦丢失或错开少许，所有修正数据全部报废［14］。而傅立叶变换的参数辨识以线带点，上位机很快分析并修正出这条曲线，找到零点。

③应用问题。实验结果满足了时栅转台在线自动标定的基本要求，参数辨识误差修正为后续的误差自修正准备了条件，同时为时栅在精密测量领域的应用奠定了基础。

参考文献：

［1］Gao Z H. Error Calibration System for Time Grating Angular Dis⁃placement Sensor［C］.Proceedings of 2012 International Confer⁃ence on Nanotechnology and PrecisionEngineering，Guilin，P.R. China：AMR，2013：705-708.

［2］彭东林，李彦，付敏，等.用于极端和特殊条件下机械传动误差检测的寄生式时栅研究［J］.仪器仪表学报，2013，34（2）：359-365.

［3］武亮，陈锡候，王阳阳，等.磁导调制型时栅位移传感器测量方法研究［J］.传感技术学报，2014，24（8）：1043-1048.

［4］黄沛，郑方燕，冯济琴，等.纳米时栅传感器高精度激励信号源研究与设计［J］.传感技术学报，2015，28（7）：977-981.

［5］裘祖荣，陈清清，李敬杰.正多面棱体和多齿分度台角分度误差的互检［J］.光电工程，2009，36（10）：90-93.

［6］徐志鹏，洪育仙，樊奇，等.多传感器pVTt法气体流量标准装置测温方案研究［J］.传感技术学报，2015，28（5）：635-640.

［7］夏桂锁，廖城，优燕军.平行双关节坐标测量机的标定及不确定度评价［J］.光学精密工程，2014，22（5）：1227-1234.

［8］徐涛，李博，刘廷霞，等.车载光电跟踪系统跟踪转台的初始标定［J］.光学精密工程，2013，21（3）：782-789.

［9］陈锡侯，苟李，官云丽，等.基于单个读数头角位移传感器自标定方法［J］.传感技术学报，2014，2（8）：1049-1053.

［10］Watanabe T，Fujimoto H，Masuda T. Self-calibration Rotary Encod⁃er［J］.Journalof Physics：Conference Series，2005：54（1）：240-245.

［11］周立功.嵌入式系统开发与应用［M］.北京：北京航天航空大学出版社，2012：75-76.

［12］高忠华，陈锡侯，郑方燕，等.时栅角位移传感器误差修正及其测试系统［J］.仪表技术与传感器，2012，（9）：75-77.

［13］Pot TS D，T Asch E M. Numerical Stability of Fast Fourier Trans⁃forms［J］. Journal of Computational and Applied Mathematics，2008，222（2）：655-674.

［14］彭东林，刘小康，张兴红，等.谐波修正法及高精度时栅位移传感器［J］.仪器仪表学报，2006，27（1）：31-33.

张天恒（1973-），男，甘肃武威人，硕士，工程师，主要研究方向为精密仪器及机械和智能传感器，zth@cqut.edu.cn；

杨继森（1978-），男，四川成都人，博士，教授，主要研究方向为计算机辅助测试技术和智能传感器，ywei@cqut.edu.cn。

Online Automatic Calibration System for Time Grating Turntable Based on Parameter Identification*

ZHANG Tianheng1，2*，LI Zhiming1，2，YANG Jiseng1，2
（1.Engineering Research Center of Mechanical Testing Technology and Equipment，Ministry of Education，Chongqing 400054，China；2.Chongqing Key Laboratory of Time-Grating Sensing and Advanced Testing Technology Chongqing University of Technology，Chongqing 400054，China）

Abstract：A automatic method is proposed to measure error of time grating turntable online，identify parameters of model and compensating error，automatically. The system is composed of the high precision grating as reference me⁃ter，micro-controller and PC. The undetermined parameters，8 on poles and 20 within poles，are identified by the Fourier transform，to obtain coefficients of identifying error model，and to realize the real-time online error compen⁃sation. To verify the results of online automatic calibration，online automatic calibration system based on parameter identification are performed and compared with the proposed parameter identification system and optoelectronic au⁃to-collimator. Experimental results show that the parameter identification of Fourier transform，can improve the ac⁃curacy and the efficiency of calibration，and the accuracy the time gratingturntable is up to 2.8″.

Key words：time gratingturntable；automatic calibration；error compensation；parameter identification

doi：EEACC：723010.3969/j.issn.1004-1699.2016.03.027

收稿日期：2015-10-15修改日期：2015-12-01

中图分类号：TP206

文献标识码：A

文章编号：1004-1699（2016）03-0462-05