基于任务调度的无线网贪婪信道分配算法*

刘玉宾（唐山师范学院计算机科学系，河北唐山063000）



基于任务调度的无线网贪婪信道分配算法*

刘玉宾*
（唐山师范学院计算机科学系，河北唐山063000）

摘要：针对无线网络链路干扰问题，综合借鉴多处理器任务调度算法提出了一种贪婪信道分配算法，为所访问的无线网链路甄选出干扰最小的信道，并且证明了本算法的近似比率为2-1/k，其中为k为可用的正交信道数，算法复杂度为O（|E|2）。为了验证本文算法的可行性和有效性，将本文所提出的贪婪算法与随机信道分配算法和按序信道分配算法进行了实验对比。仿真结果表明：本文所提出的贪婪算法的整体性能优于其他两种算法，并且贪婪算法得到的最大干扰和平均干扰归一化值随着可用正交信道数的变化趋势较其他两种算法稳定。从而验证了本文算法能有效的降低链路干扰，一定程度上可以提升网络吞吐量。

关键词：无线网络链路；信道分配；贪婪算法；链路干扰；NP-hard；任务调度算法

项目来源：河北省高等学校科学研究计划项目（Z2015075）；唐山市科学研究计划项目（15130203a）；唐山师范学院团队建设项目（2016C08）

随着无线技术的发展，无线网络在日常生活中的应用越来越广泛。无线网状网WMN（Wireless Mesh Network）作为一种多跳无线接入网络，可以降低布设有线接入网的成本，同时也提高了在恶劣环境中布设接入网的可能性。但在布设多跳无线网络时需要考虑无线链路干扰问题，随着数据传输路径跳数的增加，链路受到干扰的可能性增大，导致网络吞吐量降低。现阶段采用多接口多信道无线路由器可应对此问题［1］，但需要考虑的一个关键问题就是信道分配。

为了解决无线网络的信道分配问题，学者对此进行了大量的研究和分析。文献［2］提出了一种分布式的信道分配算法和一种集中式的信道分配算法，贪婪算法的集中式实现复杂度为O（dK|Vc|3），分布式实现算法复杂度为O（|Vc|K），其中r为文中算法在循环过程中产生的近似解个数，d为冲突图中节点度的最大值，Vc为冲突图中节点数（原网络中的链路）。其中K为可用信道数。从算法复杂度方面考虑，在网络规模较大的情况下，该文所提的集中式信道算法并不占优势。文献［3］中给出了一种负载感知的分布式静态信道分配算法，其首先将链路按照负载由大到小排序。对负载大的链路优先分配信道，在信道分配过程中，总是优先选择干扰小的信道。所给算法是一种针对树形拓扑机构的分层信道分配算法。文献［4］给出的是一种分布式的信道分布算法，该分布式的信道分配算法需要周期性的更新各收发器的信道，维持该信道分配算法需占用网络资源。文献［5］给出一种动态信道分配算法，文章将所研究的信道分配问题映射为list-coloring问题，其信道分配由位于网关的专用信道分配服务器完成。文献［6］通过拓扑控制的方法利用网络信道，其信道分配的目标为最小化信道干扰。在文献［7］中的min-max着色图问题已证明为NP-hard问题。文献［8］结合多信道技术与时分多路访问技术的节点调度算法，提出了信道分配与时隙调整机制，在可用无线信道有限的约束条件下，实现了时隙重用并最小化有限信道约束对优化节点状态切换次数的影响。文献［9］基于分簇网络拓，提出了一种无冲突的分布式时分/频分多信道MAC协议，该协议在于充分复用了可用的多信道频率资源，提高了网络吞吐量。

文献［2-9］已对信道分配做了大量研究，在这些研究中，信道分配需要达到的目标不同，但所需解决的问题均为NP-hard问题。为了有效解决无线网络链路干扰问题，本文借鉴多处理器任务调度算法的精髓，给出一种不同于现有算法的集中式贪婪信道分配算法以解决NP-hard问题，最终实现最小化最大链路干扰。

1　网络模型

本文将全网看作一个无向图，用G=（V，E）表示，其中V表示网络中的所有节点，E表示网络中的所有链路。对于任意节点v∈V，其邻居节点的个数与节点上配备的无线接口数目一致。F={f1，f2，…，fn}表示全体数据流集合，用集合R={r1，r2，…，rn}表示各数据流在源节点的数据产生速率。每一数据流具有指定的路径，用集合P={p1，p2，…，pn}表示相应数据流的路径。当pi包含链路e时，令xie=1；否则。则链路e上的负载大小可表示为：

假设Le表示链路e的干扰范围内的所有链路（不包括链路e），ce表示链路e上分配的信道。并且d（u，v）表示节点u与节点v间的欧拉距离。通过定义1和定义2分别给出链路间距离和链路干扰范围内干扰链路的定义，通过定义3明确给出链路受到的干扰大小。

定义1链路间距离。对于链路e=（u，v）与e′=(u′,v′)，其距离定义为链路两端节点间的最小距离，可表示为：d(e,e′)=min{d(u,u′),d(u,v′),d(v,u′),d(v,v′)}。

定义2干扰链路集合。链路e的干扰范围内的链路集合为其干扰域中所有链路，即：Le={e′|d(e,e′)≤RI,e′∈E}，其中RI为节点干扰范围。而当确定在链路e上分配信道c时，真正对链路e产生干扰的链路为Le中与其采用同样信道的链路，即：Lc,e={e′|ce′=c,e′∈Le}。

定义3链路干扰大小。若链路e上分配信道c，则其受到的干扰大小为其自身流量与其所有干扰链路的流量之和，即。此值实际上也可表示链路e干扰域中信道c上流量干扰值或负载值。

令Imax为网络中各链路干扰的最大值，即Imax= me∈aEx {Ice,e}。本文的目的旨在寻找一种信道分配算法，将特定的信道C={c1，c2，…，ck}分配给网络中的链路，每个链路获得唯一的信道，最终使Imax的值最小。

2　本文算法

最小化最大链路干扰问题即为NP-hard问题［10］，为了解决NP-hard问题，本文综合借鉴多处理器任务调度算法［11］，给出了一个简单有效的贪婪信道分配算法，并详细分析其近似比率。在具体介绍贪婪信道分配算法之前，先给出多处理器任务调度问题的一般表述。

多处理器任务调度问题可描述为［12］：给定一个任务集合J={j1，j2，…，ja}，各任务彼此独立，并且任务ji的执行时间为ti，共有M个处理器，要使完成所有任务的总时长开销最短，其实就是解决典型的NP-hard问题［13］。

若将信道视为处理器，将每条链路视为一个任务，网络中的m条链路映射为调度问题中的m个任务，链路负载视为任务处理时间，则本文考虑的最小化最大链路干扰信道分配问题类似于多处理器任务调度问题。两者最大的区别在于：在信道分配问题中，链路受到的干扰并不是彼此独立的；而在多处理器任务调度问题中，各任务彼此独立。

针对链路彼此依赖的信道分配问题，本算法在考虑为链路e分配信道时，每次选择le+Ice,e值最小的信道ce分配给链路e。表1中，给出了该贪婪信道分配算法的伪代码。在定理1中，本文证明该贪婪算法的近似比率为2-1/k，其中k为可用的正交信道数。

表1　贪婪信道分配算法

定理1对于本文描述的最小化最大链路干扰信道分配问题，表1中所给出的贪婪信道分配算法为（2-1/k）-近似算法，并且该算法的时间复杂度为O（|E|2）。

证明假设η为任意最优信道分配算法，该算法得到的最大链路干扰用Iη表示。此干扰值不小于网络中任意单条链路的负载值，即：

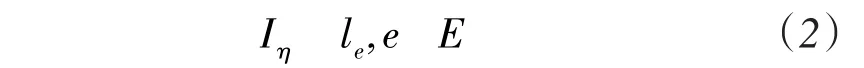
假设de表示链路e干扰范围内的链路数，并且此de条链路共利用了k′(k′≤k)个信道（k为可用的正交信道数）。由于Iη为最大链路干扰值，则其大小至少不低于其干扰范围内所有链路负载值平均值与链路e负载∑值之和。链路e干扰范围内所有链路的流量值为le′，则可得：

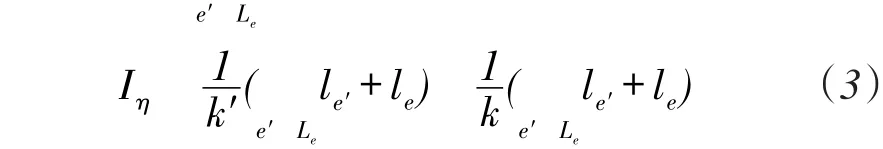
为更清楚的说明（3）式，如图1所示链路e及其干扰域中所有链路。

图1　链路e干扰范围图

假设总共有c1，c2，c33个正交信道，将信道c1分配给链路e1和e2；将信道c2分配给链路e3，e4与e5；将信道c3分配给链路e，e6与e7。则有。此干扰域中，信道c1上的干扰，信道c2上的干扰为。由于Iη为干扰最大值，则有Iη≥I（c1）以及Iη≥I（c2），进而有Iη≥（1/3）（I（c1）+I（c2）+ Iη），即为式（3）在此例中的表示。

假设Ig表示由本文所给出的贪婪信道分配算法产生的链路干扰最大值，并且该干扰发生在链路e上，所分配给链路e的信道为c*。链路信道分配算法总是选择干扰最小的信道分配给链路，则当分配给链路c (c≠c*)时，链路e上受到的干扰将不小于Ig，即，

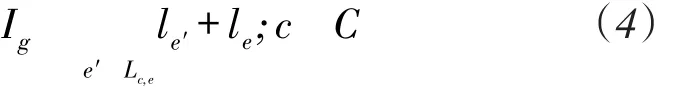
将式（4）左右两边的表达式在所有信道c∈C上累加，可得：

对式（5）进行变形，可得：

将式（2）和式（3）带入式（6）可到：

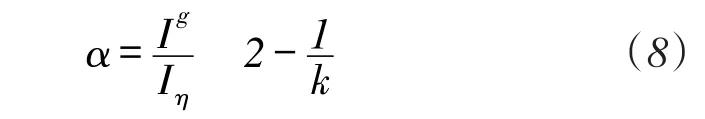
至此，证明了对于本文描述的最小化最大链路干扰信道分配问题，表1中所给出的贪婪信道分配算法为（2-1/k）-近似算法。由于表1中算法第3行需循环执行k次，而Ic，e值的计算需访问链路e的干扰链路，在任意拓扑环境下，任一链路的干扰链路数小于全网链路数|E|，故而可认为代码中第2行至第4行最差情况下需执行k|E|次。对每一链路e∈E，都需做同样的操作，考虑到k为常数，故而算法时间复杂度为O（|E|2）。

目前以最小化最大链路为目标的信道分配算法中，没有公认的最好算法，特别是针对任意网络拓扑，没有相应的算法，本文所提的信道分配算法可以应用于任意网络拓扑环境。为了进行对比分析，本文给出另外两种信道分配算法：随机信道分配算法与按序信道分配算法。

在随机信道分配算法中，当为链路e分配信道

则本文贪婪算法的近似比率为：时，从信道集合C中随机选择选择一个信道分配给链路e。表2、表3分别为随机信道分配算法与按序信道分配算法的伪代码，在算法中，随机给网络中链路编号，对于编号为label的链路，分配的信道号为“la⁃bel mode k”。本文不从理论上分析随机信道分配算法和按序信道算法的性能，将通过仿真结果进行对比分析。

表2　随机信道分配算法

表3　按序信道分配算法

3　仿真结果

本节利用Visual Studio 2013实现上述三种信道分配算法，通过仿真分析给出信道分配算法的性能。仿真中模拟两种网络拓扑：格形网络拓扑与随机网络拓扑。网络中共有100个节点，30个数据流，每一数据流具备唯一的源节点和目的节点。源节点和目的节点均从100个节点中随机选择，并且源节点和目的节点不为同一个节点。每一数据流采用的路径为跳数最少路径，数据流的速率为1 Mbit/s至10 Mbit/s之间选择的随机整数值。

由于在常用的IEEE 802.11a/b/g协议中，可支持的最大正交信道数位IEEE 802.11a提供的12个信道。故在仿真中，本文设置将可用正交信道值从1增加至12，观察各信道分配算法的归一化链路最大干扰和归一化全网链路平均干扰值。所谓归一化值即为仿真得到的干扰值对全网链路总负载进行的归一化。为便于观察，图2与图3中以归一化干扰值0.1作为基准值，给出了基准线。

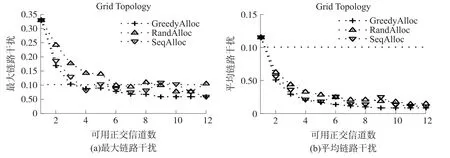
图2　格形网络拓扑链路干扰对比图

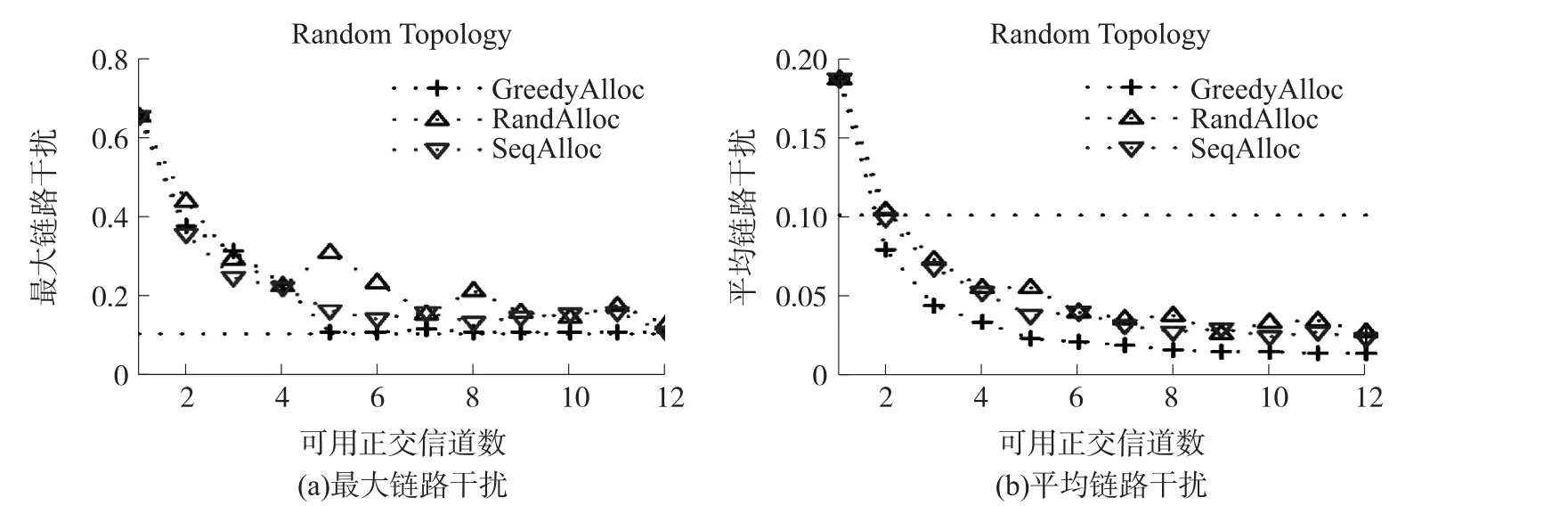
图3　随机网络拓扑链路干扰对比图

图2给出了在格形网络拓扑场景下的结果。从图2（a）和图2（b）中看出，随着可用正交信道数的增加，最大链路干扰归一化值和平均链路干扰归一化值呈现下降趋势，说明采用多接口多信道能有效降低无线网络中的干扰。对比三种信道分配算法，可以看出：不管是最大链路干扰还是平均链路干扰，贪婪信道分配算法的性能都是三者中最优的。并且从图中曲线随着信道数的变化趋势来看，贪婪信道分配算法得到的最大链路干扰和平均链路干扰是随着信道数值广义递减的，而随机信道分配算法与按序信道分配算法并不是广义递减，其变化曲线呈现曲折状态。

图3给出的为随机网络拓扑场景下链路最大干扰与平均干扰归一化值随信道数增加的变化趋势。各曲线呈现的趋势与图2中曲线类似，但对应于不同信道数值的干扰值要普遍高于图2中的值。在图3（a）中，当可用正交信道数为3时，贪婪信道分配算法得到的最大链路干扰归一化值要稍高于其他两种算法，产生这一现象的原因在于对于最小化最大链路干扰值这一问题来说，贪婪信道算法也只是一种近似算法，而绝非最优算法，在某些场景下，会存在其他算法得到的性能优于该贪婪算法。通过对三种信道分配算法的对比来看，本文所提出的贪婪算法的整体性能优于其他两种算法，并且贪婪算法得到的最大干扰和平均干扰归一化值随着可用正交信道数的变化趋势较其他两种算法稳定。当网络干扰较低时，网络的吞吐量性能则会提高。故本文所给的贪婪信道分配算法，能有效的降低链路干扰，从而提升网络吞吐量。

4　总结

最小化最大链路干扰信道分配问题归根到底就是NP-hard问题，本文提出了一种贪婪信道分配算法，为所访问链路选择干扰最小的信道，该贪婪算法为（2-1/k）-近似算法，其算法复杂度为O（|E|2）。通过模拟格形网络拓扑与随机网络拓两种网络拓扑，可以得出：在格形网络拓扑场景下，随着可用正交信道数的增加，婪信道分配算法得到的最大链路干扰和平均链路干扰是广义递减，而随机信道分配算法与按序信道分配算法呈现曲折状态，但与两种对比算法相比，更能有效降低无线网络中的干扰。而在随机网络拓扑场景下，虽然在不同可用正交信道数下，本文算法的最大链路干扰归一化值要稍高于其他两种算法，但在整体性能上优于其他两种算法。通过对比不同拓扑情况下的链路干扰值，表明在进行网络部署时，规则的格形网络拓扑性能更优。如何解决贪婪信道算法的最优化问题将是以后信道分配研究的方向。

参考文献：

［1］Ashish Raniwala，Kartik Gopalan，Tzi-cker Chiueh. Centralized Channel Assignment and Routing Algorithms for Multi-Channel Wireless Mesh Networks［J］. Mobile Computing and Communica⁃tions Review，2004，8（2）：50-55.

［2］Anand Prabhu Subramanian，Himanshu Gupta，Samir R. Das. Minimum-Interference Channel Assignment in Multi-Radio Wire⁃less Mesh Networks［J］. IEEE Transactions On Mobile Comput⁃ing，2008，7（12）：1459-1473.

［3］邱振谋.多接口多信道无线Mesh网络中的信道分配研究［D］.南京:东南大学，2011.

［4］石小川，黄传河，李楠.基于无线Mesh网络的一种信道分配算法及路由协议［J］.武汉大学学报（理学版），2011，57（2）：155-164.

［5］Krishna N. Ramachandran，Elizabeth M. Belding，Kevin C. Alme⁃roth，Milind M. Buddhikot. Interference-Aware Channel Assign⁃ment in Multi-Radio Wireless Mesh Networks［C］. Infocom 2006，2006：1-12.

［6］Mahesh K. Marina a，Samir R. Das b，Anand Prabhu Subramani⁃an. A Topology Control Approach for Utilizing Multiple Channels in Multi-Radio Wireless Mesh Networks［C］. Broad Nets 2005，2005：381-390.

［7］Arunesh Mishra，Suman Banerjee，William Arbaugh. Weighted Coloring Based Channel Assignment in WLANs［J］. ACM Sigmo⁃bile Mobile Computing and Communications Review，2005，9（3）：19-31.

［8］曾波，李珊珊，王辉.一种基于有限信道的能量高效节点调度机制［J］.传感技术学报，2015，28（2）：254-258.

［9］张龙妹，史浩山，陆伟. DTFMM：一种适应于WMSNs的多信道MAC协议［J］.传感技术学报，2011，24（3）：452-456.

［10］Mercedes Hidalgo-Herrero，Pablo Rabanal，Ismael Rodriguez，et al. Comparing Problem Solving Strategies for NP-hard Optimiza⁃tion Problems［J］. Fundamenta Informaticae，2013，124（2）：1-25.

［11］Garey，Michael R，Johnson，David S. Computers and Intractabili⁃ty：A Guide to the Theory of NP-Completeness［M］. W. H. Free⁃man and Company，238.

［12］杨辉华，张晓凤，谢谱模，等.基于布谷鸟搜索的多处理器任务调度算法［J］.计算机科学，2015，42（1）：86-87.

［13］Graham R L. Bounds for Certain Multiprocessing Anomalies［J］. Bell System Technical Journal，1966，45：1563-1581.

刘玉宾（1981-），男，汉族，河北乐亭人，硕士，唐山师范学院讲师，研究方向：无线传感性能优化与仿真、物联网技术，liuyubing_81@126.com。

Greedy Channel Assignment Algorithm for Wireless Networks Based on Task Scheduling*

LIU Yubin*
（Department of Computer Science，Tangshan Normal University，Tangshan Hebei 063000，China）

Abstract：Aiming at the problem of link interference in wireless networks，this paper proposes a greedy channel al⁃location algorithm based on multi processor task scheduling algorithm，which is the minimum channel for the access link selection. At the same time，the approximate ratio of the proposed algorithm is 2-1/k，and the k is the available orthogonal channel number，and the complexity of the algorithm is O（|E|2）.In order to verify the feasibility and effec⁃tiveness of the proposed algorithm，the proposed algorithm is compared with the random channel assignment algo⁃rithm and the random channel assignment algorithm. The simulation results show that the overall performance of the proposed algorithm is better than the other two algorithms，and the maximum interference and average interference normalized values obtained by the greedy algorithm are more stable than the other two algorithms.So the algorithm can effectively reduce the link interference，and can improve the network throughput in acertain degree.

Key words：wireless network link；channel allocation；greedy algorithm；NP-hard；task scheduling

doi：EEACC：6250Z；7220；6150P10.3969/j.issn.1004-1699.2016.03.021

收稿日期：2015-10-10修改日期：2015-12-05

中图分类号：TP393

文献标识码：A

文章编号：1004-1699（2016）03-0429-05