半球谐振陀螺仪频率裂解及固有刚性轴的测试方法

李　巍，金　鑫，任顺清（.哈尔滨理工大学自动化学院，哈尔滨50030；.哈尔滨工业大学空间控制与惯性技术研究中心，哈尔滨5000）



半球谐振陀螺仪频率裂解及固有刚性轴的测试方法

李巍1*，金鑫1，任顺清2
（1.哈尔滨理工大学自动化学院，哈尔滨150030；2.哈尔滨工业大学空间控制与惯性技术研究中心，哈尔滨150001）

摘要：半球谐振陀螺仪以其寿命长、可靠性高、体积小、重量轻、精度高而且可微型化的优点将在卫星、潜艇等导航领域有着广泛的应用前景。对半球谐振陀螺仪的而言，频率裂解值与固有刚性轴的位置是其关键的技术指标，因此设计测试方案对其进行精确测试是十分必要的。根据陀螺仪工作原理，从理论角度进行了推导，建立存在频率裂解及与固有刚性轴不重合时谐振子的运动方程，通过研究主驻波及辅助波的表达式，进而得到了振动位移的精确表达式，最后设计了在固定位置安装两组激励电极以及两组位移传感器对频率裂解以及固有刚性轴位置进行测试的测试方案，并给出了最佳的测试时间。

关键词：导航；半球谐振陀螺仪；频率裂解；固有刚性轴；电极；位移传感器

半球谐振陀螺是目前精度最高的哥氏振动陀螺，与传统陀螺相比，在结构上不存在高速转子和活动支承，它的稳定性好、噪声低、分辨力高、寿命长、可靠性高，具有抗核辐射等功能，在卫星，星际航行中有着广阔的应用前景，因此受到惯性技术界的极大关注［1-6］。

上世纪80年代～90年代，我国开始了半球谐振陀螺仪的理论研究。十·五期间，中电集团二十六所成功研制出半球谐振陀螺仪样机，十一·五期间研制的产品在性能上有了很大改进，在此基础上，国内半球谐振陀螺仪的研究及应用逐步兴起，对半球谐振陀螺仪的信号检测技术、误差分析、控制技术等进行了广泛研究［7-12］。

如果陀螺仪振型的方位与固有刚性轴之一的方位重合，那么振型将是驻波，否则，振型将发生进动，从而影响陀螺仪的精度，如果频率裂解值过大，也将对陀螺仪的精度产生影响［13-15］。目前，对于频率裂解值以及固有刚性轴的测试问题进行研究的文献较少，而且所设计的测试方案比较复杂［16］，因此，为了达到提高陀螺精度的目的，对频率裂解值以及固有刚性轴的方位进行精确且相对简单测试是十分必要的。

本文将针对频率裂解值和刚性轴位置的测试进行研究。

1　固有刚性轴与频率裂解介绍

对固态波陀螺谐振子中驻波特性产生最实质性影响的是诸如密度、杨氏模量、薄壳的壁厚等参数的不均匀性的傅里叶展开式的第四次谐波。偏差四次谐波的存在导致谐振子中出现两个相互间展成45°的两个固有轴系，谐振子沿这两个轴中的每个轴振动的固有频率都能达到极大和极小值如图图1所示。极大值和极小的频率差称作固有频率的裂解：

ω2-ω1=Δ（1）

固有频率较小的固有轴称为“重的”；固有频率较大的轴称为“轻的”。在固有轴方面还有一个术语：大固有频率的轴称为大刚度轴，小固有频率的轴称为小刚度轴。使用“重量的”还是“刚性的”术语来称呼取决于所描述的物理过程是怎样的。

驻波将随着时间而破坏，谐振子中的振动过程可以表示为带各种频率的两个谐波振动和形式。

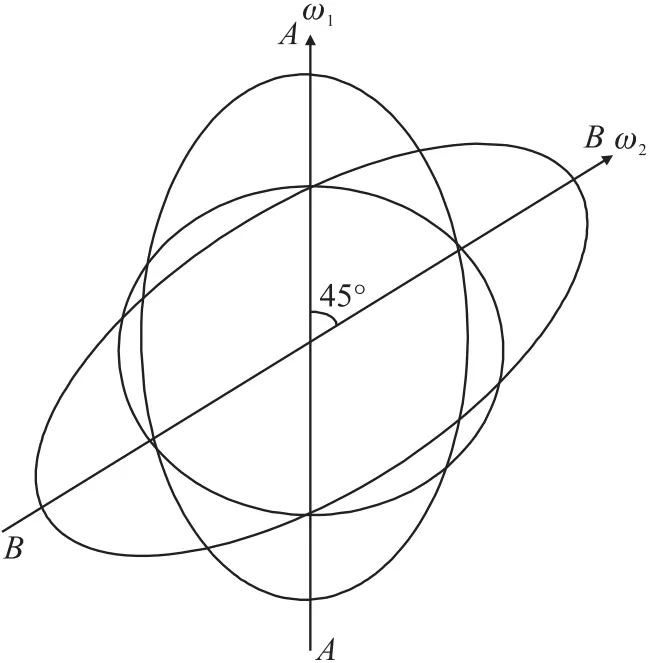
图1　固有刚性轴

2　存在频率裂解及不对准固有刚性轴时谐振子的运动方程

通常采用的谐振子位置式激励原理图如图2所示，其中，X为一对激励电极，Y为位移传感器，当激励电极X激励出的波时，位移传感器Y用来测量节点处驻波的振动，两者之间夹角为45°。

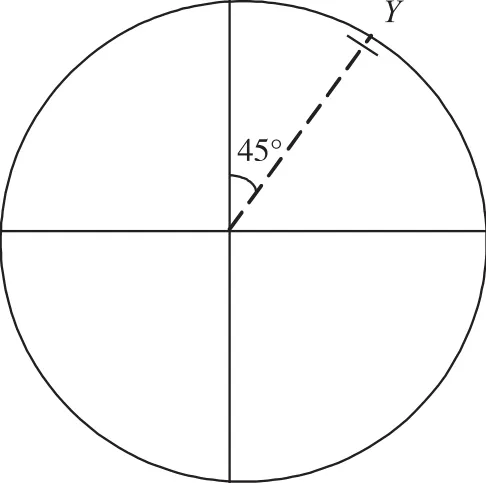
图2　位置激励的原理图

首先，激励电极X通电，激励出振型，然后切断激励电极X的电压，激励波处于自由振动状态，此时谐振子的运动方程为：

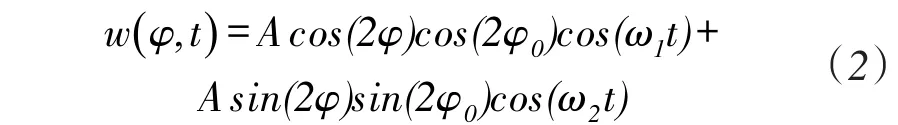
式中：ϕ0为波相对固有刚性轴的方位。取谐振子固有频率w0，使得ω1<ω0<ω2，令：

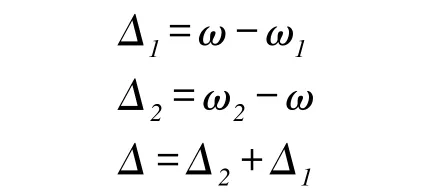
则式（2）变为：

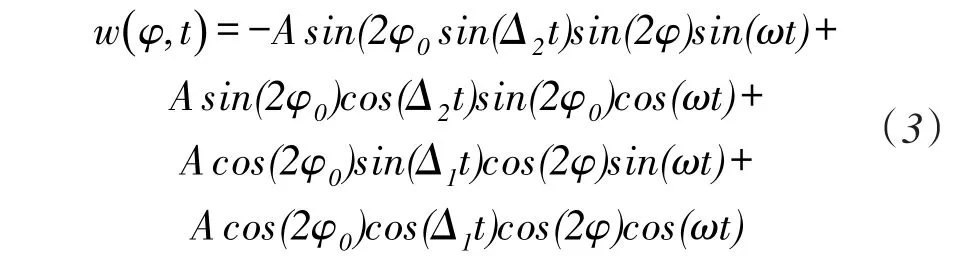
设式（3）的系数矩阵为P，根据式（3）则P的行列式：

当det P=0时，式（3）表示的过程为驻波。根据式（4）只有当φ0=0,π 4，振型的初始方位与某一固有刚性轴的方位重合时，波动过程才为驻波；只有当研究波动过程的时间t满足：Δt≪1时，式（4）才“几乎”满足驻波条件，此时的波动过程可以看做两个按圆周角和瞬时相位相互正交的驻波耦合。此时令参数a为：

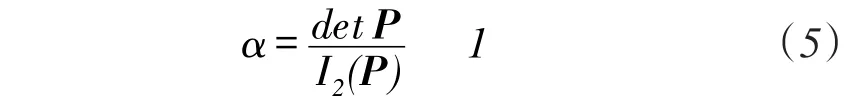
式中：I2(P)=a2+b2+m2+n2。

P可表示为

矩阵X，Y分别为两个驻波的系数矩阵，且有detX=detY=0，以X为系数矩阵的主驻波，以Y为系数矩阵的辅驻波。

可知如果主驻波是式（2）表示的波动过程的最佳逼近，根据式（6），则有

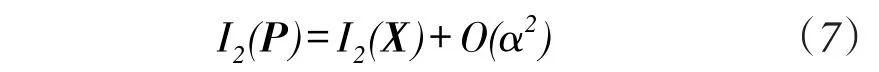
式中：O(α2)为接近0的高阶小量。

根据式（6），I2(P)可表示成以下形式：

式中：α2I2(Y)为2阶小量。

根据式（7）以及式（8），如果式（7）成立，那么有下面关系：

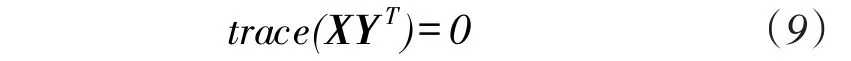
设存在矩阵S，使Y=S-1XS，为满足式（5-45），S取以下形式：

根据式（10），式（8）可改写成以下的形式

改写式（11）

式（12）按a的线性逼近，：

根据式（13），可以确定称辅驻波的系数矩阵Y的形式为

根据式（4）和式（5），得到

设主驻波的系数矩阵X为

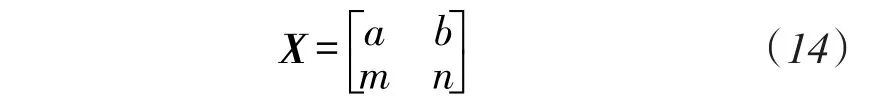
根据式（13），式（14）以及式（4），得到主驻波的矩阵X的系数a，b，m，n：

主驻波形式的为：

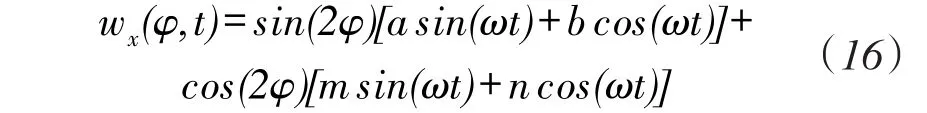
考虑到Δ1t≪1和Δ2t≪1，而a值有与Δ1，Δ2值相同的阶，故而舍去a与Δ1，Δ2的乘积项，只保留a的一次项，得到：

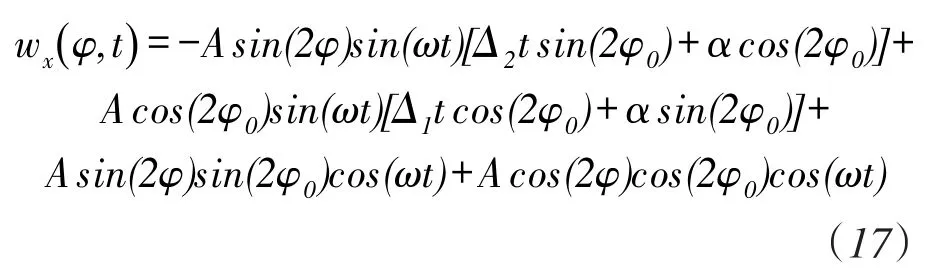
基本变换后可写成表达式：

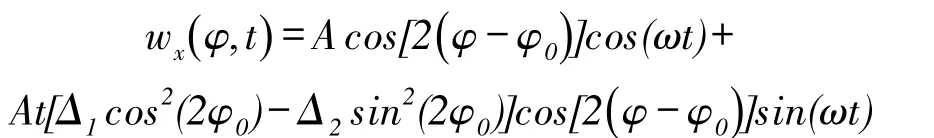
或

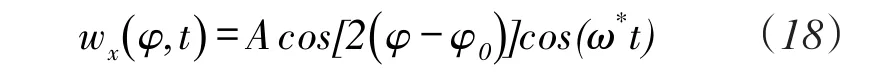
式中，ω*=ω1cos2(2φ0)+ω2[sin2(2φ0)]

根据式（18）进一步得到辅驻波的表达式：

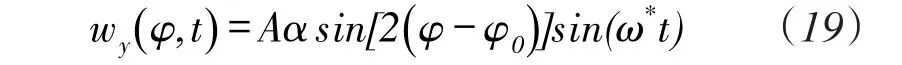
综上，振动位移表达式（2），可表示为：

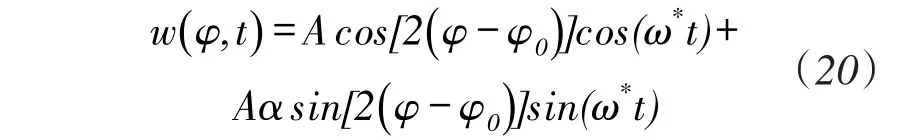
从式（20）可以看出，对于单点位置激励，谐振子的运动方程中包含了固有刚性轴位置及频率裂解的相关量，将会对陀螺仪的精度产生影响，因此对其进行测试是十分必要的。

3　频率裂解及固有刚性轴的测试方法

根据前面的分析，设计了一种双激励电极双位移传感器的测试方案。所提出的频率裂解值和固有刚性轴位置测试图如图3所示，其中A、B分别为一对激励电极，C、D分别为位移传感器，设激励电极B处为0度，角度沿顺时针方向，电极A与电极B以及位移传感器C、D之间的夹角都为22.5°，j4为距离位移传感器D最近的固有刚性轴的角度。当激励电极A激励出的波时，位移传感器C用来测量节点处驻波的振动，另一个位移传感器D用于测量激励电极B激励的驻波在节点处的振动。

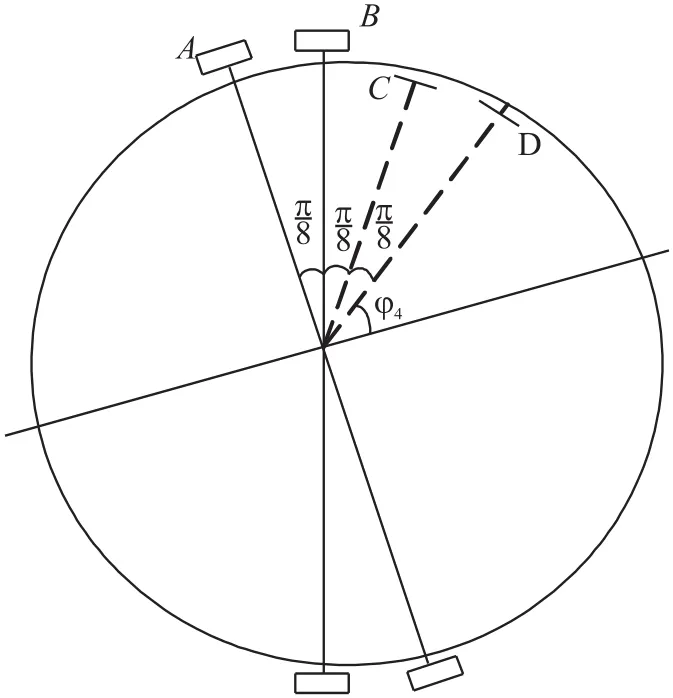
图3　频率裂解值和固有刚性轴位置测量图

利用位移传感器C来检测节点处信号的位移，以固有刚性轴位置为基准，以逆时针方向为正，则节点处j0以及j相应值为

将式（21）代入到式（20）中，C处的波动过程可以表示以下形式

则位移传感器C处检测的信号幅值为

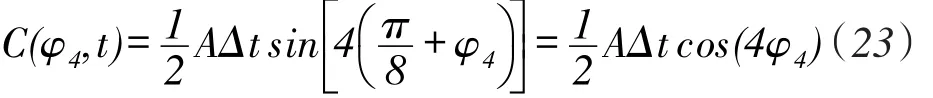
可将幅值A表示为如下形式

式中：A0为激励波的常值幅值；t表示切断激励电极后至采样时刻的时间（s）；

根据式（24），式（23）可改写为：

同理，接通激励电极B，激励出振型后，切断激励电极B的电压，此时位移传感器D检测到的信号为

根据式（25）以及式（26）可以看出检测得到信号的幅值是与检测时间有关的，因此得到最好的辨识效果，需要在信号幅值最大的时刻进行检测，图3为信号幅值随时间变化曲线图。由图4可见当采样时间t=64 s时，位移传感器检测到的信号幅值最大。

图4　信号幅值随时间变化趋势图

根据式（25）以及式（26）得到，频率裂解值以及固有刚性轴位置的数学计算公式分别为：

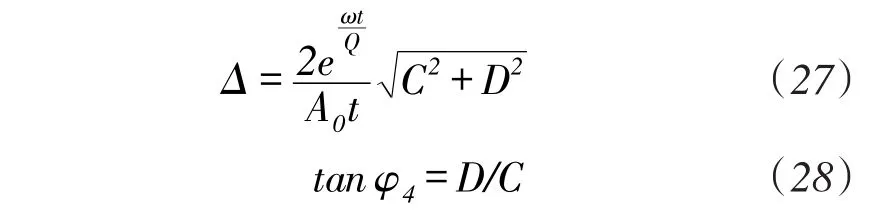
式中，采样时间t为64 s。

由式（27）、式（28）可以看出，当采用设计的测试方案时，只需要采集两个位置传感器的输出信号，就可以得到频率裂解与固有刚性轴的精确数值。

因此，可以利用两组激励电极和位移传感器，根据式（27）及式（28）对半球谐振陀螺仪的频率裂解值以及固有刚性轴的位置进行测试计算。相对于中所选用的16电极测试方案［15］，本文设计测试方案只使用了两组激励电极和两个位移传感器，更加简单有效。

4　结论

设计了半球谐振陀螺仪的频率裂解值以及固有刚性轴位置的测试方案，并给出了试验的最佳采样时刻。设计试验对半球谐振陀螺仪的技术指标的测试是十分有意义的，可以对半球谐振陀螺仪的性能有更加直观的了解，也为提高陀螺仪的精度进行补偿提高了相应的理论依据。

参考文献：

［1］吕志清.半球谐振陀螺（HRG）信号处理技术［J］.中国惯性技术学报，2000，8（3）：58-61.

［2］Matthews A，Rybak F J. Comparison of Hemispherical Resonator Gyro and Optical Gyros［J］. IEEE Aerospace and Electronics Sys⁃tems Magazine，1992，7（5）：40-46.

［3］任顺清，李巍，赵洪波.对准误差对半球谐振陀螺仪输出精度的影响［J］.振动测试与诊断，2011，31（4）：420-423.

［4］Wi Uiam B. Scott，Delco Makes Low-cost Gyro Prototype［J］. AW & ST，1982，117（17）：64-67.

［5］何传五.几种新型陀螺简介［J］.航天控制，2001，19（2）：73-80.

［6］王旭，方针，吴文启，等.基于二维质点振动模型的半球谐振陀螺仪谐振子进动分析［J］.中国惯性技术学报，2011，19（5）：621-626.

［7］李广胜，蒋英杰，孙志强，等.基于AR多变量模型的半球谐振陀螺仪温度漂移建模［J］.传感技术学报，2009，22（10）：1442-1445.

［8］王旭，吴文启，方针，等.力平衡模式下半球谐振陀螺仪正交误差控制［J］.仪器仪表学报，2012，33（4）：936-940.

［9］陆学斌，刘晓为，陈伟平，等.振动式微机械陀螺的带宽特性分析［J］.传感技术学报，2008，21（2）；337-340.

［10］赵洪波，任顺清，霍帅军，等.开环位置激励半球谐振陀螺仪工作原理与误差分析［J］.压电与声光，2013，35（1）：51-58.

［11］高胜利，吴简彤.基于多电极的半球谐振陀螺仪信号检测［J］.哈尔滨工程大学学报，2008，29（5）：474-478.

［12］李巍，任顺清，赵洪波.比力对半球谐振陀螺仪解算精度的影响［J］.中国惯性技术学报，2011，19（5）：603-606.

［13］李巍，任顺清，王常虹.半球谐振陀螺仪谐振子品质因数不均匀引起的误差分析［J］.航空学报，2013，34（1）：121-129.

［14］任顺清，赵洪波.半球振子密度分布不均匀对输出精度的影响［J］.中国惯性技术学报，2011，19（3）：364-368.

［15］马特维耶夫B A，利帕特尼科夫B И，阿廖欣А В，等.固体波动陀螺［M］.杨亚非，赵辉，等译.北京：国防工业出版社，2009：26-36.

［16］Shatalov M，Coetzee C. Dynamics of Rotating and Vibrating Thin Hemispherical Shell with Mass and Damping Imperfections and Parametri cally Driven by Discrete Electrodes［J］. Gyroscopy and Navigation，2011，2（1）：27-33.

李巍（1982-），男，博士，毕业于哈尔滨工业大学，讲师，哈尔滨理工大学大学自动化学院，参加多项省部级课题项目，研究方向为精密检测技术，曾以第一作者发表多篇学术论文被工程索引（EI）等国际检索机构收录，leenwei901@163.com。

Measurement of Frequency Splitting and Inherent Rigidity Shaft of Hemispherical Resonator Gyro

LI Wei1，JIN Xin1，REN Shunqing2
（1.School of Automation，Harbin University of Science and Technology，Harbin 150030，China；2.Space Control and Inertial Technology Research Center，Harbin Institute of Technology，Harbin 150001，China）

Abstract：Hemispherical resonator gyro（HRG）has a wide application prospect in fields of satellite，submarine etc，which has the features of high precision reliability，long life span，small volume，light-weight，high-precision and be⁃ing miniaturized. Frequency splitting and inherent rigidity shaft are very important specification for HRG，therefore，it is necessary to design the measurement to identify that. According to the operational principle of the gyroscope，the radial vibration equation of resonator is established while the frequency splitting and inherent rigidity shaft are taken into account，by studying the expression of the main wave and auxiliary wave，the exact expression of vibra⁃tion displacement is given，the measurement and identification method of frequency splitting and inherent rigidity shaft using two groups of electrodes and displacement sensors was designed，and the optimal sample time was given too at last.

Key words：navigation；hemispherical resonator gyro；frequency splitting；inherent rigidity shaft；actuator；displace⁃ment sensor

doi：EEACC：063010.3969/j.issn.1004-1699.2016.03.006

收稿日期：2015-09-09修改日期：2015-11-23

中图分类号：V249.32

文献标识码：A

文章编号：1004-1699（2016）03-0338-05