谈陀螺定向在独立坐标系中的应用

刘坤，张杰胜

（中铁四局集团，安徽 合肥 230041）

谈陀螺定向在独立坐标系中的应用

刘坤，张杰胜

（中铁四局集团，安徽 合肥 230041）

在地下工程洞内导线测量中，加测陀螺定向边是消除角度误差的积累。在工程独立坐标系下，地面已知边精度已经确定、陀螺仪已经选定、作业人员已经固定情况下，文章提出了合理地选取地面已知边以减小△的影响，采用合理的计算方法提高γ的计算精度，既方便外业操作又简化了内业计算，保障了陀螺定向工作的可靠性。

陀螺定向；仪器常数；子午线收敛角；独立坐标系

1 概述

在地下工程洞内导线测量中，受到测角误差和起始方位角误差的影响，随着导线节点的增加，点位的横向误差也在逐步地积累，导线的终点表现得更为明显[1]。为了解决导线测量引起的方向误差积累，通常加测陀螺定向[2]，校核导线测量中的测角误差，并将其作为已知条件参与导线测量平差，以提高导线的精度，减小贯通误差。

陀螺定向的北方向是陀螺北方向，其方向与真北方向有个常数差△。真北方向与坐标北方向之间也存在着一个夹角，称作子午线收敛角。三者之间的夹角又称作三北方向改正角[3]。

2 影响待定边方位角精度的因素

图1 三北方向示意图

如图1所示，N为真北方向，NT为陀螺北方向，Nx是坐标北方向。陀螺北方向NT与真北方向之间的夹角，称为仪器常数，用△表示。陀螺子午线位于地理子午线以东△为正，反之为负。真北方向N与坐标北方向Nx之间的夹角称为子午线收敛角，用γ表示，其符号由安置仪器的位置确定，在中央子午线以东为正，以西为负。图中精密导线边CD的坐标方位角为α0，子午线收敛角为γ，αt为其陀螺方位角。在实际工作中，真北方向角A0是未知的，需要求解。C点为仪器设站点，那么有：

由（1）、（2）可得：

仪器常数△的误差包括了已知边坐标方位角的误差、仪器操作误差以及外部环境的影响。

在地铁陀螺定向工作中，需要用地面已知求解△来计算地下待定边的坐标方位角。这里地下待定边的坐标方位角用αt下表示，仪器常数用Δ′表示，子午线收敛角用γ下表示，那么有：

根据误差传播定律可得：

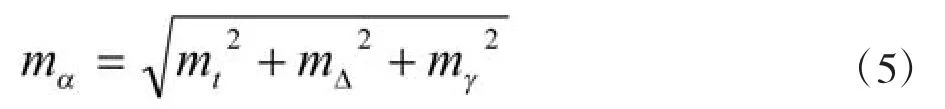
除去地面控制网的测角误差之外，定向边坐标方位角的精度，取决于定向边陀螺定向精度、仪器常数和子午线收敛角三个方面的因素。在实际工作中，在已知边上测定仪器常数以及在定向边上测定陀螺方位角，陀螺定向测量的中误差mt可认为是定值。在已知点坐标精度固定的情况下，要提高待定边坐标方位角的定向精度，主要从仪器常数△和子午线收敛角γ两方面进行分析。

3 仪器常数的适用范围

在（3）和（4）式中，对于地下待定边的仪器常数，文中给出了不同于地面已知边测定的仪器常数的表示方法，两条边上测量的常数值是否相等。传统观念中都是认为常数值是等值代换，将式(3)的值直接可以代入（4）式中进行计算，限定条件是测定仪器常数的已知边宜与地下定向边的平面位置尽量接近[4]，没有量化标准。要提高陀螺定向的精度，这直接关系到已知边位置的选择[5]。

在精密导线控制网中，选定一条边作为基准边，与这条边不同的距离和方向上分组选择导线边作为验证边，在选择的所有导线边上都进行陀螺定向测量，并记录相应的气象条件，求算各条边上仪器常数，然后进行不同距离和不同角度的边上与已知边的测定的仪器常数统计分析，总结有如下规律：

①已知边与定向边之间的距离小于2000m时，仪器常数比较稳定。超出这个范围，仪器常数会有较大的变化。

②已知边与定向边的相对方位的不同对仪器常数产生的影响较小。

③已知边与待定边的测量环境温差要控制在10℃之内。

4 子午线收敛角的计算精度

子午线收敛角可由大地坐标（B，l）计算，也可以由平面坐标（x，y）计算，在《控制测量学》[6]给出了相应的计算公式：

式中：l为测站到中央子午线的经差；B为测站纬度；t=tanB；；η=e′cos2B；e为第一偏心率，e′为第二偏心率。

（6）、（7）两个公式计算精度高，由于计算量大，在实际工作中常采用简化公式，计算量小且计算精度满足规范精度的要求[7]。

上述的子午线收敛角计算公式，平面坐标（x，y）均为相对于中央子午线投影后得到的自然坐标，而在工程施工中常采用的是独立坐标系的坐标，计算时注意加以区分。在计算工程施工的独立坐标系的子午线收敛角时，首先要根据投影自然坐标与独立坐标之间的坐标转换参数关系，将独立坐标恢复为自然坐标再代入公式进行计算。

在无转换参数和无法确定γ的正负号的情况下，无法直接使用上述公式，可按以下方法解决。

当已知边和待定边距离较近，满足前述的要求时，可认为Δ=Δ′，将（3）式代入（4）式，有：

角可以从电子地图上查出，ρ和Nf取常数值，代入（9）式可得：

将（11）代入（10），有：

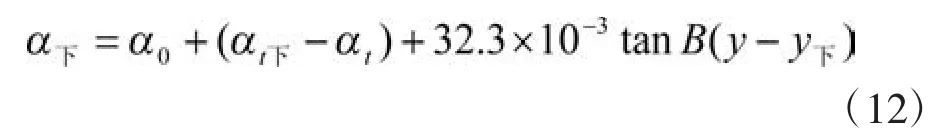
式中收敛角是计算两者的差值，无论是独立坐标或是自然坐标，两点之间的坐标值之差是相同的，且收敛角的正负号取决于设站点y坐标差，这样就无需进行坐标转换和设站点位置判断了。

5 实例验证

成都轨道交通7号6标线流科区间控制网，设计提供了控制网的独立坐标系的坐标，如表1所示。这里我们将GPS023→KAN1这条边作为地面已知边，将边ZTL775→Z682和边YTL505→Y570作为待定边，地图上查得测区纬度310。经过陀螺定向和计算后得到待定边的坐标方位角，将之与控制网已知坐标方位角进行比较，看较差是否满足规范要求，用于验证测量及计算方法的可靠性。控制点坐标见表1，导线边位置示意图见图2。

控制网坐标 表1

图2 导线边位置示意图

①陀螺定向观测

基准边陀螺方位角测量精度评定 表2

检核边陀螺观测计算表 表3

②待定边方位角计算

将数据代入（12）式可得：

检核边ZTL775→Z682方位角：

检核边YTL505→Y570方位角：

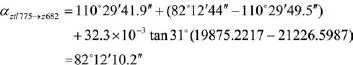
③坐标方位角检核

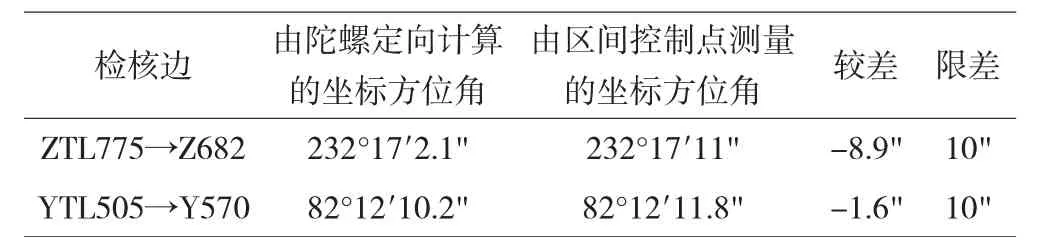
坐标方位角较差 表4

6 结论

本文研究了陀螺定向工作中已知边和待定边的位置关系对仪器常数的影响，提供施工现场在陀螺定向已知边位置选取的参考依据；在独立坐标系控制网下的陀螺定向工作中，在未知自然坐标转换参数的情况下，通过公式原理的推导方便地解算出子午线收敛角，并通过坐标差值的正负取代了关于设站位置相对于中央子午线位置的正负号判断，合理方便地解决了类似工程项目在陀螺定向工作中存在的问题。

[1]谢平，刘元志.陀螺全站仪在矿山测量方面的运用[J].国土资源导刊，2013（5）：92-95.

[2]尹志强，盛剑，张秋芳.陀螺全站仪在地铁联系测量中的应用[J].测绘与地理空间信息，2012（S1）：123-124.

[3]张正禄.工程测量学[M].武汉：武汉大学出版社，2005.

[4]GB50308-2008，城市轨道交通工程测量规范[S].

[5]胡荣明.陀螺定向时已知边位置的选择 [J].西安科技大学学报，2007（6）：260-262.

[6]孔祥元，郭际明.控制测量学[M].武汉：武汉大学出版社，2009.

[7]邬熙娟，江国焰，高俊强.子午线收敛角计算公式及其计算精度的分析[J].现代测绘，2005（12）：22-25.

TU198+.6

B

1007-7359（2016）06-0170-03

10.16330/j.cnki.1007-7359.2016.06.066

刘坤（1978-），男，毕业于武汉大学，硕士；高级工程师。研究方向：精密工程测量。