重载列车拨车机动态载荷模型及速度曲线优选

魏　伟， 王　厂， 张　渊， 赵旭宝

(1.大连交通大学 交通运输工程学院，辽宁 大连　116028；2.齐齐哈尔轨道交通装备有限责任公司大连研发中心，辽宁 大连　116052)



重载列车拨车机动态载荷模型及速度曲线优选

魏伟1， 王厂2， 张渊1， 赵旭宝1

(1.大连交通大学 交通运输工程学院，辽宁 大连116028；2.齐齐哈尔轨道交通装备有限责任公司大连研发中心，辽宁 大连116052)

摘要：据列车纵向动力学理论建立拨车机动态仿真模型，考虑缓冲器强非线性特性、车钩间隙效应、车辆启动及运行阻力等因素开发出拨车机动态载荷仿真系统。通过列车拨车试验数据验证模型的有效性，据出口拨车机系统初始设计速度曲线预测4万吨列车拨车载荷。结果表明，初始设计速度下拨车机最大载荷为1 414.9 kN。通过对4万吨列车速度曲线的优选保证拨车效率及每次拨车距离，拨车机载荷较原方案下降30%，时间缩短5 s。该动态仿真系统可为重载列车拨车机设计提供新手段。

关键词：重载列车；车辆动力学；拨车机；翻车机

拨车机作为翻车机系统重要组成部分，可拨送列车到指定位置准确停车，且直接影响翻车机系统制造成本及翻卸效率。拨车机设计载荷过大会增加成本；过小则不能满足翻卸效率需要。随列车牵引吨数不断增加拨车力亦不断增加，拨车过程中车辆缓冲器变形非常显著，会产生明显的伸缩效应，加之缓冲器的强非线性而使拨车机动态载荷设计十分复杂。目前，国内拨车机最大拨送列车为1万吨，但出口4万吨列车拨车机给设计提出更高要求，且散装卸货方式逐渐由人工向机械化过渡，而大多发电厂、码头、钢铁公司等亦用机械化翻车机系统卸煤碳、矿石。

我国主要以5 000吨列车为主，车身短、重量轻，所需拨车力较小，缓冲器变形亦小。列车基本以整体运动为主，拨车机载荷设计较简单，主要以最大加速度为依据，利用牛顿第二定律计算最大拨车机载荷作为固定值，称为静态载荷，并据此设计电机及传动装置。随被牵引列车长度、重量增加，拨车机动力不断增大，用静态载荷计算方法会使拨车机出现极大能力浪费。在长大列车拨车过程中列车缓冲器会出现较大伸缩效应，致拨车过程中列车产生较大纵向振动。无论施加牵引力或制动力均与列车纵向伸缩振动相关，载荷为非常复杂的动态过程。缓冲器变形时拨车力传递需时间过程，并非所有车辆同步受力，此与静态载荷计算完全不同，因此将考虑列车伸缩效应的拨车力称为动态拨车载荷。因传统静态拨车机载荷设计已不能满足要求，而动态设计是发展趋势，属于列车纵向动力学研究范畴。纵向动力学因重载列车快速发展而产生，由于车钩断裂、疲劳事故频发，列车纵向动力学日益得到重视。Ansari等[1]通过模拟方法研究缓冲器刚度、车钩间隙、制动对车钩力影响。Chou等[2]研究电控制动下重载列车车钩力问题表明，电控制动可明显提高制动同步性、减小车钩力。Belfarte等[3]用MATLAB仿真环境研究欧洲重载列车纵向动力学问题。文献[4]对大秦线2万吨列车进行系统试验研究。耿志修[5]开发列车纵向动力学仿真系统，研究列车纵向冲动问题。魏伟等[6]用仿真方法研究两万吨列车纵向动力学问题。魏伟等[7]据仿真结果分析纵向冲动机理，认为重载列车最大车钩力由挤压力或冲击力产生，并提出降低挤压力、冲击力途径。魏伟等[8]针对列车纵向冲动制动激励获取难题，提出模型化列车空气制动系统新方法。魏伟等[9]开发空气制动与纵向动力学仿真系统，可彻底解决列车纵向动力学仿真中制动时激励载荷问题。尽管列车纵向动力学问题研究已取得重要进展及成果，但有关低速运行的拨车机拨车过程牵引载荷研究较少。拨车机牵引载荷大小不仅关系翻车机系统卸载能力，且对拨车机结构设计、成本、价格及寿命均有显著影响。郝映非[10]以齿条传动拨车机为例对其载荷谱、电机功率确定及匹配进行分析、探讨，但有关重载列车拨车机动态载荷设计研究较少。

本文介绍基于列车纵向动力学的拨车机动态仿真原理，通过试验数据验证仿真系统的准确性，并仿真某公司出口的4万吨列车初始设计速度曲线的拨车载荷，在运输效率不降低条件下提出以降低拨车机载荷为目标的新速度曲线。

1拨车机动态仿真系统

据刚体动力学基本原理，将列车离散成一系列质量-弹簧阻尼系统，仅考虑列车纵向自由度，每个车辆离散成一个集中质量，缓冲器离散成弹簧阻尼装置，见图1。

图1　列车动力学模型Fig.1 The model of train

每个车辆(集中质量)在任何时刻的受力见图2。

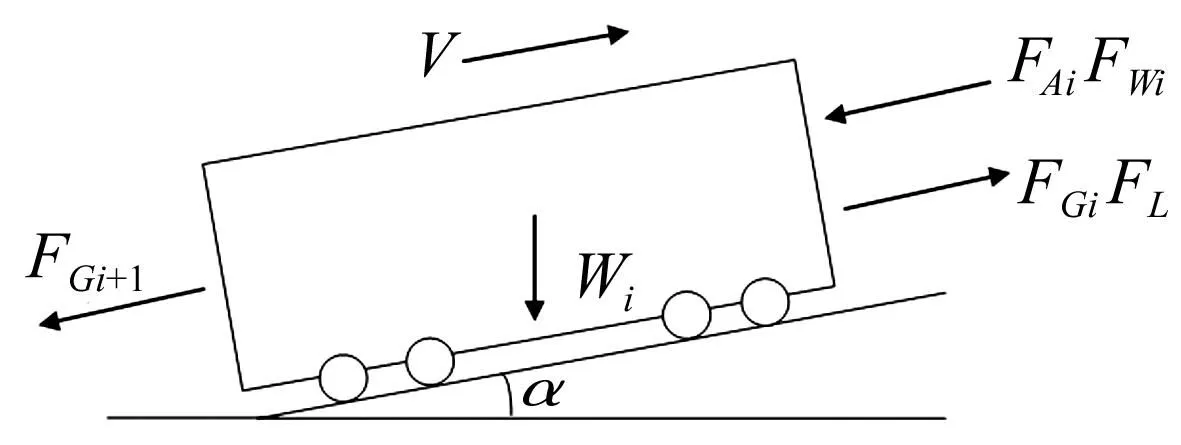
图2　单个车辆受力图Fig.2 The force acting on one vehicle

任意瞬时，每个机车或车辆(集中质量块)受力有前后车钩力FGi(t)，FGi+1(t)、运行阻力FAi(t)、坡道阻力FWi(t)、曲线阻力FRi(t)及拨车机所在位置的拨车力FL(t)。则第i车运动方程为

FWi(t)-FAi(t)-FRi(t),(i=1～n)

(1)

式中：FG1(t)=0；FGn+1(t)=0；n为列车中所含车辆总数。

当i为对应的拨车机时，FL(t)即为拨车力，否则，FL(t)=0。车钩力FGi(t)可据两车相对位移、速度由缓冲器模型获得。运行阻力据列车牵引计算规程[11]计算，方法如下：

车辆为重车时单位重量基本阻力为

w0=0.92+0.004 8v+0.000 125v2

(2)

车辆为空车时单位重量基本阻力为

w0=2.23+0.005 3v+0.000 675v2

(3)

式中：v为列车运行速度(单位km/h)。

FAi(t)=migw0

(4)

式中：mi为第i车质量。

据列车牵引计算规程,启动阻力取3.5 N/kN。据文献[12]，低速运行时基本阻力与“规程”中阻力略有不同，为满足此需求，在系统中设置对话框输入阻力方式，可手动输入运行阻力及启动阻力。

附加阻力包括坡道附加阻力及曲线阻力，据“规程”，单位重量坡道阻力等于坡道坡度千分数，即wi=k，其中k为坡道坡度，上坡取正值，下坡取负值。曲线阻力据“规程”规范计算，计算方法为：

列车长度小于或等于曲线长度时单位重量曲线阻力为

(5)

式中：R为曲线半径(单位m)。

列车长度大于曲线长度时单位重量曲线阻力为

(6)

式中：ll为列车长度；lr为曲线长度，单位m。

牵引计算中曲线长度含圆曲线长度及两端缓和曲线各半长度，计算式为

(7)

式中：Lr为曲线总长，单位m；lyz1，lyz2为曲线两端缓和曲线长，单位m。

缓冲器特性为影响列车纵向冲动的重要因素，本文借鉴文献[9]缓冲器模型，设缓冲器作用力与两车相对速度、相对位移相关，并考虑车钩缓冲装置的整体间隙，即

(8)

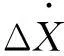
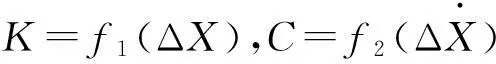
找到缓冲器刚度与阻尼函数后利用模型仿真计算不同速度的单车撞击单车冲击。各种速度下冲击模型均能较好表达缓冲器特性。本文所用某型号缓冲器在相对速度4 km/h冲击下的车钩力及缓冲器压缩量关系即缓冲器特性曲线见图3。图中箭头指向文缓冲器压缩回弹运动方向，车钩力为0的平台即为车钩间隙影响，间隙越大平台越长。由图3可看出缓冲器强非线性与车钩间隙影响。缓冲器压缩过程中较明显的环至少有4个，最大环为缓冲器第1次压缩回弹，所形成的环面积即为缓冲器在第1循环消耗的能量。第1大环结束后有1车钩力为零的平直段，此由车钩间隙造成，在该阶段车钩力为0，过车钩间隙后在缓冲器压缩量正值范围又出现1压缩环，相对第1大环减小许多，此后在压缩量为负值、正值范围出现几个小环，且每个环越来越小。该缓冲器模型在列车纵向动力学仿真中已用较长时间，各工况列车纵向动力学仿真结果与试验结果吻合度较好。

图3　4 km/h冲击时考虑车钩间隙的缓冲器特性曲线Fig.3 The draft gear characteristic with slack under 4 km/h initial velocity

2拨车机动态载荷仿真系统有效性验证

为验证基于列车纵向动力学的拨车机动态载荷仿真系统准确性，在华能营口电厂进行拨车机运行试验。共测试一列车，该车由55节车箱组成，测试每拨送一次的拨车机动态载荷，共试验55次。选车钩尾部及大臂应变较大区域作为测试贴片区，如大臂正面及对应背面，测试拨车力。在移动平台牵引齿轮上安装拨片测试平台速度。采用两套试验测试系统，即日本共和动静态应变采集系统、德国IMC动态信号采集系统。测试现场见图4，55次试验最大拨车力见图5。由图5 看出，最大拨车力变化趋势随拨车次数增加(列车中车辆数目越少)拨车力越小。最大拨车力试验结果有一定离散性，造成离散的原因可能为前一次拨车停车状态不同，车钩拉压状态不完全一致及拨车速度不同所致。

图4　拨车机试验现场Fig.4 Experiment site

据最大拨车力试验结果，拟合拨车力与拨车次数关系曲线，表达式为

y=562.171 8-7.192 4x

(9)

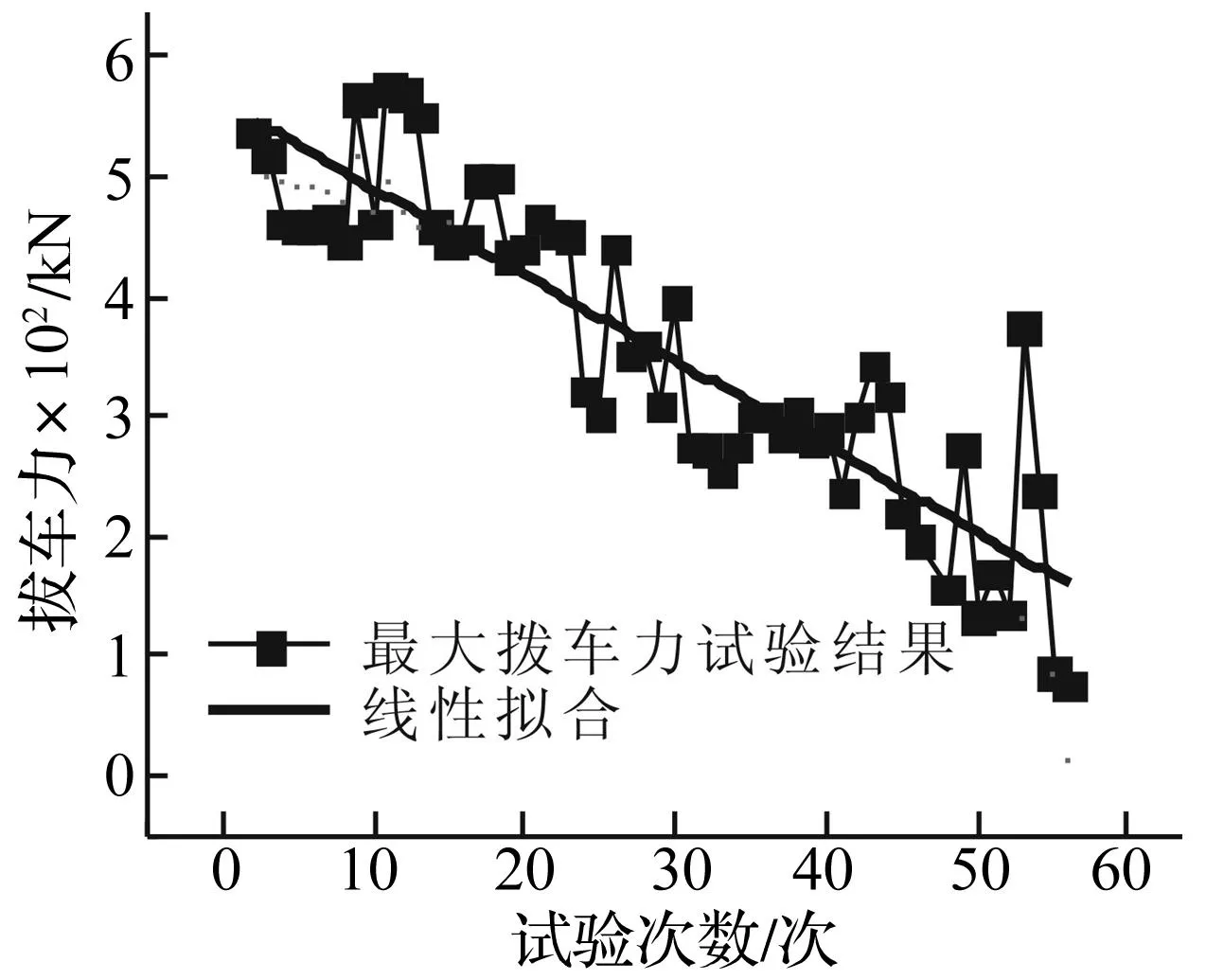
图5　试验最大拨车力图Fig.5 Maximum force of experiments

用拨车机动态载荷仿真系统计算相同条件下拨车机牵引力，并与试验结果拟合曲线进行对比，见图6。由图6看出，第35 次试验前仿真结果处于试验结果中部，基本代表试验结果平均值。第35 次后仿真值略小于试验值，表明仿真模型在车辆数目较少时尚需进一步完善。

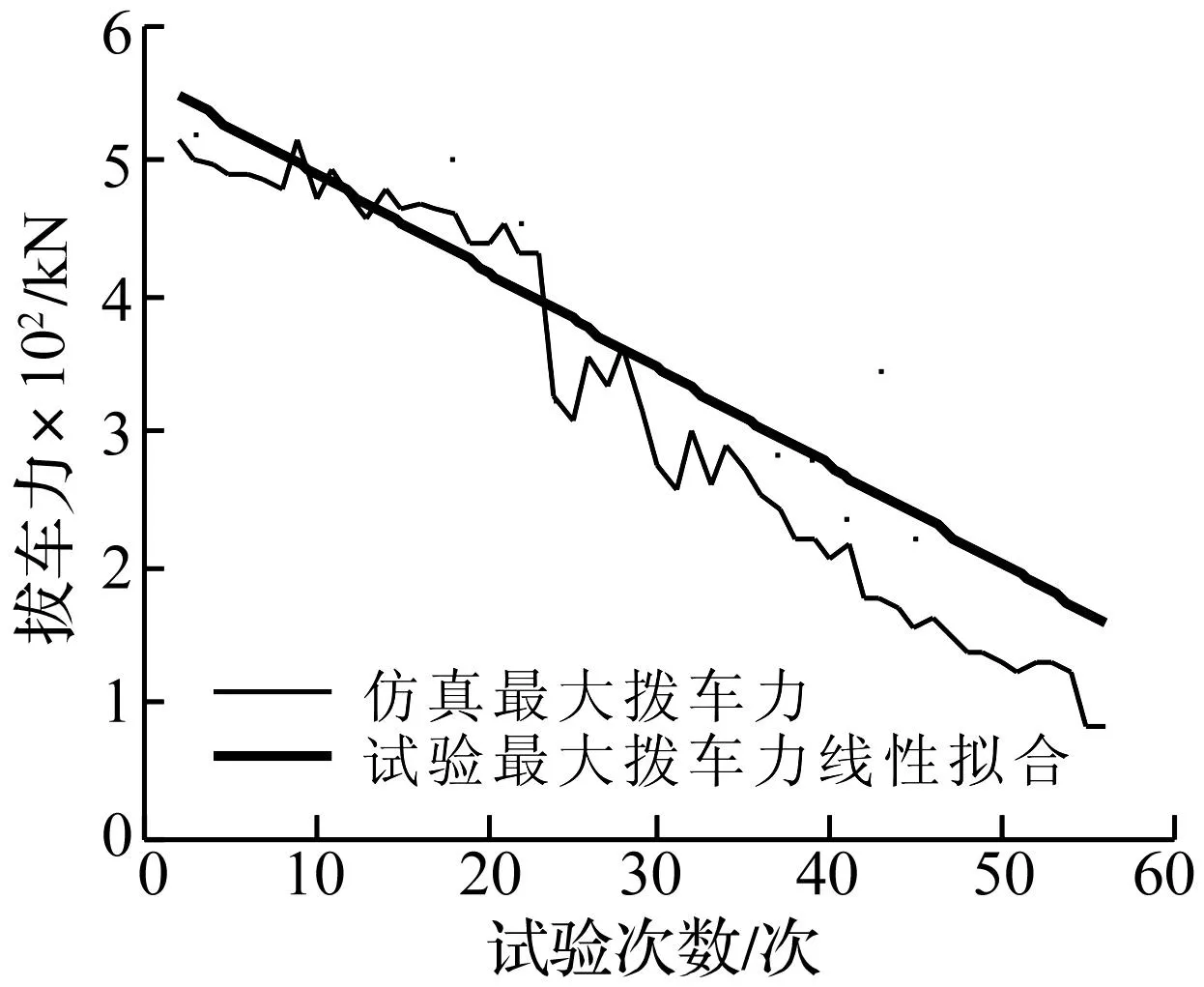
图6　仿真最大拨车力图Fig.6 Maximum force of simulation

3四万吨列车拨车载荷仿真

目前国内最长拨车列车为1万吨，若拨送更长列车缺乏应用经验。据某厂出口澳大利亚4万吨翻车机系统要求设计拨车机运行速度曲线。列车由2台机车及240节重车组成。机车位于列车头部，每台自重196 t，长23 m，每辆车重160 t，长12 m，空车重22.5 t，整车总重38 596 t。拨车机速度曲线见图7，加速阶段2 s，加速到0.55 m/s，该速度持时54 s接两个减速段：第1段0.5 s，减速到0.18 m/s；两减速段有1恒速区段，恒速时间30.7 s；第2减速段0.8 s，完整拨车时间88 s，一次拨车走行距离为36 m。

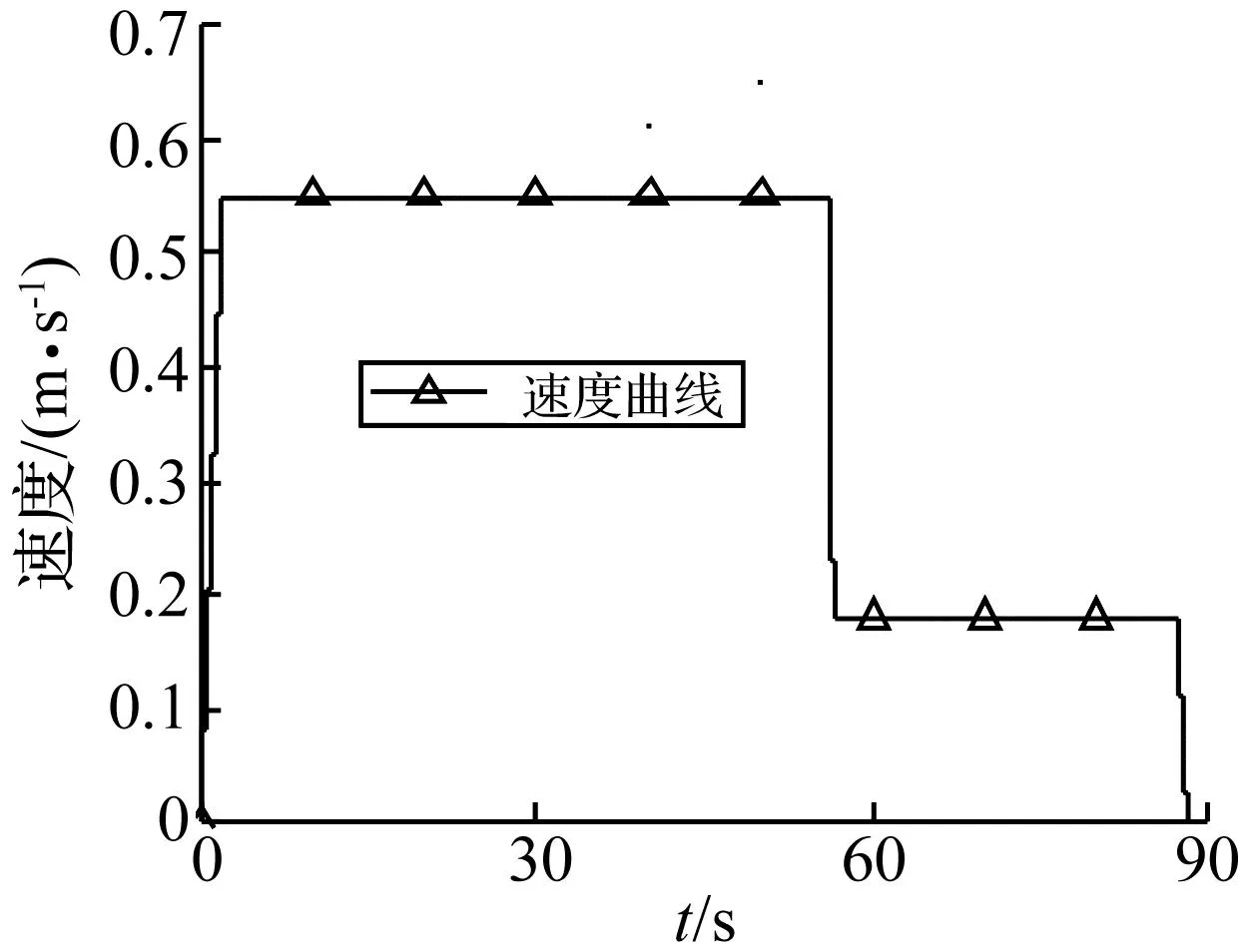
图7　4万吨列车初始设计速度曲线Fig.7 Initial design velocity for 40 000 t train

由以上条件所得拨车力仿真计算结果见图8。由图8看出，拨车力在加速终点时(2 s)产生991.5 kN峰值，之后短时下降再缓慢增加，在恒速段末尾55.6 s时达最大值1 414.9 kN后开始下降，直到停车。

图8　4万吨拨车载荷预测图Fig.8 Predictive chart of indexer load for 40 000 t train

由拨车力仿真曲线及计算中间结果可知，加速阶段只有少量车开始加速，大量车处于静止并未运动，故在加速段末尾拨车力并未达最大。当拨车机进入恒速阶段后由静止转向运动的车辆不断增多，拨车力不断加大。开始减速阶段拨车力达最大值，加速车辆最多，因列车较长并未达到所有车辆全部加速。若列车较短，在恒速阶段所有列车加速完毕，则在减速阶段开始前拨车力应达最大值。由此推断，通过适当修改加速阶段持时及恒速阶段运行速度可能会降低拨车力最大值。

4四万吨列车拨车速度优选

由于列车较短基本以整体形式运动，因此拨车机牵引速度主要靠经验亦能满足设计要求。拨送重载列车时，由于列车编组较长，加之动态效应影响较大，简单据经验设计拨车机速度已不能满足要求。4万吨列车拨车机速度初始设计曲线表明仍有余地对拨车机载荷进行优选，载荷优选有两种方式，即不增加拨车机载荷下缩短拨车时间、提高拨车效率及拨车周期不变条件下降低拨车机载荷。

本文优选据拨车机制造厂要求，保证拨车机最高运行速度不高于0.55 m/s，拨车时间不大于88 s，走行距离为36 m，且以降低最大拨车力为目标。拨车机速度曲线由5部分组成，即：加速阶段、第1次匀速阶段、第1次减速阶段、第2次匀速阶段、第2次减速阶段。最大拨车力发生在拨车机第1次加速后恒速运行阶段(图8)，主要因恒速阶段车辆启动逐渐增多，若不增加速度，仅靠已加速车辆带动会降低最大拨车力，因此对原恒速阶段速度逐渐降低，适当修正原恒速阶段后的速度，以确保整个拨车过程走行距离不变。原速度曲线及2种新设计速度曲线见图9。其中优选1曲线速度由0匀加速2.5 s到0.55 m/s后匀速运行22.5 s，再以弧线形式减速到0运行85 s行走36 m，最高运行速度仍为0.55 m/s；优选2曲线无匀速阶段，加速阶段结束后直接以弧线形式减速到0，运行83 s行走36 m，最高运行速度为0.54 m/s。

图9　4万吨列车优化速度曲线Fig.9 Optimized velocity curves

原速度与2种优选速度曲线拨车力见图10。其中原始曲线第1峰值为991.5 kN，最大值为1 414.9 kN；优选1曲线第1峰值为876.8 kN，最大值为1 029.1 kN；优选2曲线第1峰值为989 kN，且为最大值；优选1方案将最大拨车力减小385.7 kN，减幅27%，拨车时间缩短3 s，缩短幅度3.4%；优选2方案将最大值减小425.9 kN，减幅30%，将拨车时间缩短5 s，缩短幅度5.7%。两种方案不仅能减小最大拨车力、缩短拨车时间，且提高拨车效率。

图10　4万吨列车优化拨车力曲线Fig.10 The hauling load for optimized velocity

据以上初选结果，翻车机厂方已针对设计方案进行改进。

5结论

据列车纵向动力学原理建立拨车机动态载荷仿真模型，采用拨车机动态仿真系统仿真计算4万吨列车在不同速度曲线下拨车载荷，以减小最大拨车力、缩短拨车时间为目标，对4万吨列车速度曲线进行优选，结论如下：

(1)本文所用拨车机动态载荷仿真模型与实验结果吻合较好，能预测拨车机动态载荷。

(2)四万吨列车在原设计速度曲线条件下最大拨车载荷发生在恒速阶段，最大拨车载荷为1 414.9 kN。

(3)对传统的拨车速度曲线，较短列车的最大车钩力可能发生在加速阶段，而长车最大车钩力可能发生在恒速阶段。

(4)对长列车在恒速阶段利用前车带后车可降低最大车钩力，优化速度曲线。

(5)本文所提两种速度优化曲线与原设计速度曲线相比，方案1可降低最大车钩力27%，拨车时间缩短3 s；方案2可降低最大车钩力30%，拨车时间缩短5 s。

参 考 文 献

[1] Ansari M, Esmailzadeh E, Younesian D. Longitudinal dynamics of freight trains[J]. International Journal of Heavy Vehicle Systems, 2009, 16(1/ 2):102-131.

[2] Chou M, Xia X, Kayser C. Modeling and model validation of heavy-haul trains equipped with electronically controlled pneumatic brake systems [J]. Control Engineering Practice,2007, 15(4) : 501-509.

[3] Belforte P, Cheli F, Diana G, et al . Numerical and experiment al approach for the evaluation of severe longitudinal dynamics of heavy freight trains[J]. Vehicle System Dynamics, 2008, 46(Sup1):937-955.

[4] 中国铁道科学研究院. 大秦线HXD1机车牵引2万吨组合列车试验报告[R]. 北京:中国铁道科学研究院, 2007.

[5] 耿志修,李学峰,张波.大秦线重载列车运行仿真计算研究[J]. 中国铁道科学,2008, 29(2): 88-93.

GENG Zhi-xiu,LI Xue-feng,ZHANG Bo. Simulation study of heavy haul train operation on datong-qinhuangdao railway[J]. China Railway Science, 2008, 29(2): 88-93.

[6] 魏伟,赵连刚. 两万吨列车纵向动力学性能预测[J]. 大连交通大学学报, 2009,30(2):39-43.

WEI Wei,ZHAO Lian-gang. Prediction of longitudinal dynamic coupler force of 20 000 tons connected train[J].Journal of Dalian Jiaotong University,2009,30(2):39-43.

[7] 魏伟,张东芹,张军. 重载列车纵向冲动机理及参数影响[J]. 大连交通大学学报,2011,32(1):1-6.

WEI Wei,ZHANG Dong-qin,ZHANG Jun. Study of longitudinal impulse mechanism and parameters impact of heavy haul train[J]. Journal of Dalian Jiaotong University,2011,32(1):1-6.

[8] 魏伟.列车空气制动系统仿真的有效性[J]. 中国铁道科学,2006,27(5):104-109.

WEI Wei. The validity of the simulation for train air brake system[J]. China Railway Science,2006,27(5):104-109.

[9] 魏伟,赵旭宝,姜岩,等.列车空气制动与纵向动力学集成仿真[J]. 铁道学报,2012,34(4):39-46.

WEI Wei,ZHAO Xu-bao,JIANG Yan,et al. The integrated model of train air brake and longitudinal dynamics[J].Journal of the China Railway Society,2012,34(4):39-46.

[10] 郝映非.拨车机牵引载荷分析[J].大重科技,2001(4):13-17.

HAO Ying-fei. Analysis of the indexer hauling load[J]. Dalian Heavy Duty Machinery Science and Technology,2001(4):13-17.

Simulation of indexer dynamic load of heavy haul trains

WEIWei1,WANGChang2,ZHANGYuan1,ZHAOXu-bao1

(1. College of Traffic and Transportation Engineering, Dalian Jiaotong University, Dalian 116028, China;2. Dalian Development Center of Qiqihar Rail Traffic Equipment Co., Ltd., Dalian 116052, China)

Abstract:The simulation model for indexer dynamic load in this work was established based on the train longitudinal dynamics theory. In the model, the important factors of the strong nonlinear characteristics of draft gear, coupler slack effect, and the vehicle starting and running resistance are considered. The indexer test data was used to validate the model. According to the 40 000-ton train indexer initial design speed curve, the dynamic load was predicted for the 40 000-ton trains. Under the initial design speed condition, the indexer maximum load is 1 414.9 kN. After optimization of the velocity curve, the optimization scheme to ensure dumping efficiency, and the train moving distance, the maximum load decreases by 30% of the original design, which shortens the time for 5 s. This dynamic simulation system provides a new tool for heavy haul indexer load design.

Key words:heavy haul train; vehicle system dynamics; indexer; car dumper

中图分类号:U270.11

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.06.029

收稿日期：2014-11-19修改稿收到日期：2015-03-20

基金项目：铁道部科技研究开发计划项目(2012J012-F)；辽宁省教育厅基金项目(L2012168)

第一作者 魏伟 男，博士，教授，博士生导师，1963年生