复合材料梁结构应力波传播特性研究

冯勇明， 周　丽， 杨建元， 袁晚春

(1.北京航空工程技术研究中心，北京　100076； 2.南京航空航天大学 机械结构力学及控制国家重点实验室，南京　210016)



复合材料梁结构应力波传播特性研究

冯勇明1,2， 周丽2， 杨建元1， 袁晚春2

(1.北京航空工程技术研究中心，北京100076； 2.南京航空航天大学 机械结构力学及控制国家重点实验室，南京210016)

摘要：基于铁木辛柯梁理论，研究含半无限大分层复合材料梁结构中波的反射与透射。考虑表面无接触压力(张开分层)及表面完全接触(闭合分层)两种极端分层条件，对单向复合材料梁建模导出反射与透射矩阵，计算能量反射与透射系数。数值结果表明，能量反射与透射系数同随波频率及分层位置变化，能量传输遵循守恒定律。研究各模态能量分配，描述前两阶弯曲波及第一阶膨胀波间模态转换关系；通过有限元仿真验证该理论分析的正确性。

关键词：分层；反射与透射；能量传输；能量分配

分层作为复合材料最易出现的损伤形式，不仅会导致刚度下降，且会影响结构承载能力、完整性、振动特性及稳定性，从而导致结构失效。文献[1-2]分析含分层及不均质梁结构的振动问题，但仅限于含分层梁的振动特性(如固有频率、振型)。研究表明，分层损伤引起的前几阶固有频率及模态参数改变不敏感。当瞬态波在含分层梁结构中传播时[3-4]，由损伤区域产生的反、透射波会携带损伤诸多本质属性。文献[5-6]研究弯曲波在分层梁中的传播，因分层引起总体弯曲刚度下降，分层区域弯曲波波速也会减小。Ostachowicz等[7]建立分层梁的有限元谱分析模型，获得由分层损伤引起的额外波包即反射波信号，但未考虑分层区域子梁间相互作用。以上文献均未考虑瞬态波能量传输问题，而其中往往含较多用于识别损伤的信息。文献[8-9]分别由理论、试验研究梁结构的能量传输，但未进一步研究入射波与反射波及透射波关系。Bazer等[10]导出含分阶面的三维介质中平面波能量流通解，由分界面、边界处微分方程获得平面反、透射波，考虑能量平衡问题，入射波能量流等于反射波与透射波能量流之和，验证能量守恒。Wang等[11]研究含分层或不均质各项同性梁的波传播问题，但只考虑分层闭合情况，数值计算只给出对称分层用于不均质比较。因此，全面研究瞬态波在复合材料梁分层处的反、透射及模态转换非常必要。

本文基于铁木辛柯梁理论，用谱分析方法描述含半无限大分层复合材料梁结构中波动，见图1。对分层区域用两种极端情况模拟波动过程中分层表面的应力条件，即①设分层表面完全张开，表示分层后的两根子梁之间无接触压力，进入子梁中的透射波不会相互干扰；②设分层表面完全闭合，表明在分层表面存在接触压力，且两根子梁耦合在一起。

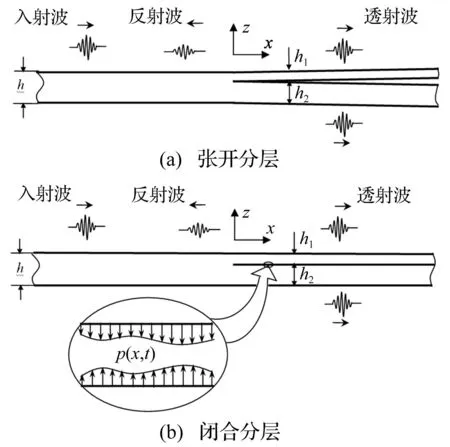
图1　半无限大分层梁中瞬态波的传播 Fig.1 Transient wave propagation in beams containing semi-infinite crack

1弥散关系

以梁轴向为x轴建立笛卡儿坐标系，基于铁木辛柯梁理论，复合材料梁的位移可描述为

(1)

式中：u(x,t)为梁轴向位移；ψ(x,t)为梁截面绕y轴转角：w(x,t)为梁横向(z向)位移。

据式(1)，应变分量可写为

εx=u,x+zψ,x，γxz=w,x+ψ

(2)

对称铺层复合材料梁平衡方程可表示为

(3)

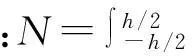
对单层正交各项异性复合材料，其刚度矩阵为

(4)

由于梁厚度方向的剪应变视为常量，引入剪切校正因子κ使横向剪力与实际情况相符。考虑y向平面应变梁，本构关系可简化为

σx=C11εx，τxz=κ2C55γxz

(5)

式中：κ2=π2/12为横向剪切校正因子。

N=A11u,x,V=κ2A55(w,x+ψ),M=D11ψ,x

(6)

式中：A11，A55，D11为拉伸、剪切、弯曲刚度，分别定义为

(7)

式(3)可表述为位移微分方程，即

(8)

对平面波解，位移可表达为

u=U0ei(kx-ωt)，w=W0ei(kx-ωt)，ψ=Ψ0ei(kx-ωt)

(9)

弯曲波动弥散关系可通过式(8)获得，即

(κ2A55k2-I1ω2)(D11k2+κ2A55-I2ω2)-

(10)

式(10)有4个解，分别为

(11)

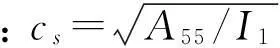
低频范围内铁木辛柯梁存在一对传播波(正、反向传播)加两个耗散波(近场波)。该对传播波(k为实数)称为最低弯曲模态A0波。两近场波(k为纯虚数)可视为沿正、反向衰减的耗散波。载波频率超过截止频率时两对传播波(两列正向传播，两列反向传播)同时存在，称为A0，A1模态。即随频率增加其中一列非传播波衰减越慢，最终变为传播波；A1模态截止频率可令k2= 0获得，即

ωc=κcs/q

(12)

相速度、群速度分别描述为

cp=ω/k,cg=dω/dk

(13)

频率接近无穷大时波速变为非弥散，两阶弯曲波群速度可据式(10)、(13)简化为

cg1=κcs,cg2=cl,ω→∞

(14)

可见两群速度值与梁厚无关。

式(8)第2、3式的通解可写为

(15)

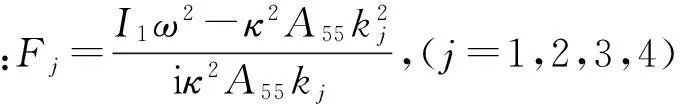
对基于铁木辛柯梁理论的非弥散膨胀波，波数可表达为

(16)

2入射与反射系数

一列入射波传播到不连续分界点处(分层尖端)时将部分反射回去、部分透射过去。而反射波与透射波幅值及相位均由反射、透射系数确定。在单向复合材料梁远场处激励的弯曲波视为入射波，其可同时产生传播波(k为实数)及近场波(k为纯虚数)。考虑张开、闭合两种极端分层条件分别导出反、透射系数。

2.1张开分层

考虑分层梁结构(图1(a))，设坐标原点在分层尖端。整梁可分为左右两区域，左区域为未分层区域并含入、反射波；右边分层区域可视为由上下两子梁组成，由于分层表面张开的，两子梁互不干扰。故分层区域只存在正向传播的透射波。

考虑一列沿x正向传播的弯曲波，在梁左区域(x≤0)波场由正向传播的入射波w0及反向传播的反射波ψ0组成，而在分层尖端处除弯曲波反、透射现象亦会出现转换的膨胀波模态。左区域内反方向传播的膨胀波u0可描述为

(17)

为书写简洁、推导方便，省略时间指数项e-it。当激励频率低于截止频率时(ω<ωc)，第二阶弯曲波为耗散波，波数k2为纯虚数。考虑反射波场趋于无限远处(x→-∞)时为有限值，波数k2应选负号。系数a，b代表入射波前两阶弯曲模态幅值并取决于具体加载方式。在低频区域内入射波中第二阶弯曲波为耗散波，不会传播能量，且幅值沿x向成指数下降，最后消失。

在右边区域(x≥0)，u1，w1，ψ1，u2，w2，ψ2描述两子梁位移场，下标1，2分别标识上、下面子梁。在该区域只有透射波存在，因此整个位移场通解可描述为

(18)

式中：上标(1)、(2)分别表示每根子梁的不同参数及位移分量。此参数可通过子梁刚度、密度、转动惯量等参数求得。

据式(16)，膨胀波波数与厚度无关，即ke=ke(1)=ke(2)。

为表示反射波与透射波幅值引入9个未知变量，即ar，br，cr，at(1)，bt(1)，ct(1)，at(2)，bt(2)，ct(2)，可由反、透射系数矩阵与已知入射波联系。通过在分层尖端(x=0)的位移连续条件及平衡条件建立方程组，即

(19)

将式(17)、(18)结合式(6)代入式(19)，得矩阵表达式为

(20)

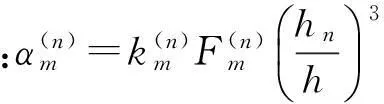
由式(20)可导出联系反、透射波与入射波间直接关联表达式为

(21)

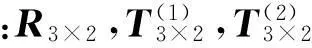
反射系数矩阵分量描述前两阶弯曲模态与第一阶膨胀模态间转换关系，如R12表示由二阶弯曲模态入射波转换为一阶弯曲模态反射波系数。同样，透射系数矩阵亦描述各模态间转换系数。弯曲波进入分层区域后同时出现弯曲波与膨胀波，其二者间的转换值得研究，且转换率随激励频率、分层位置而变化。

2.2闭合分层

(22)

接触压力p可通过将式(22)中第1式与第3式相加消去，合成为

(23)

设平面波位移场为

(24)

将式(24)代入式(23)及式(22)第2、4式中，分层区域弥散关系可描述为

(25)

由于子梁间耦合效应，分层区域有3个弯曲模态，两截止频率可通过式(25)中令波数为0获得，即

(26)

当频率接近无穷大时3阶弯曲模态的群速度解析表达式可由式(13)、(25)导出

(27)

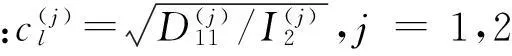
对矩形截面单向复合材料梁，其横、纵波速度在分层、未分层区域均一致，且可认为单层复合材料中横、纵波速度，只与材料密度、刚度有关。因此，分层区域两截止频率与3个群速度在频率趋于无限大时可写为

(28)

显然，式(28)第1式表明两截止频率与张开分层条件下两单独子梁一阶截止频率时一致。通过比较式(28) 第2式与式(14)，两种条件下弯曲模态群速度具有相同趋势。

在闭合分层区域正向传播的透射波位移场通解可描述为

(29)

式中

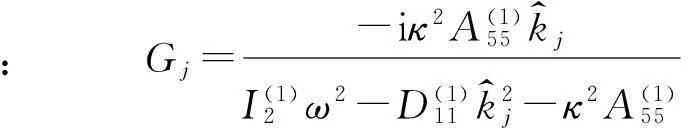
: Gj=-iκ2A(1)55k^jI(1)2ω2-D(1)11k^2j-κ2A(1)55

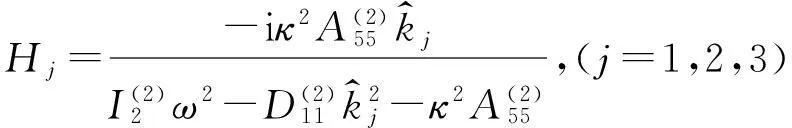
两子梁的膨胀波模态与张开分层条件下一致。8个未知变量ar，br，cr，at，bt，dt，ct(1)，ct(2)可通过分层尖端(x=0)处连续、平衡条件确定，即

(30)

将式(17)、(29)结合式(6)代入式(30)，用矩阵描述为

(31)

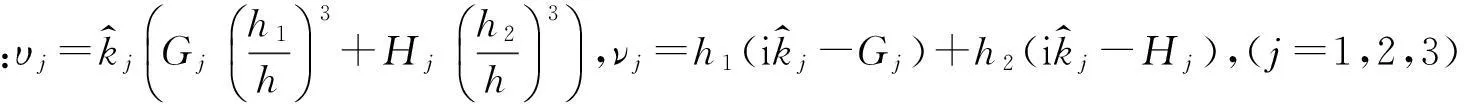
反、透射波与入射波间关联表达式为

(32)

式中：R3×2，T5×2为反、透射系数矩阵。

对完全接触的分层表面，透射系数矩阵含三阶耦合的弯曲模态与两子梁两阶膨胀模态。因此，模态转换系数与张开分层条件下有所不同。

3能量反射与透射

波传播过程中不断传输能量，在单位时间内流进一个截面的能量应等于流出能量。能量传播速度或称为能量流可通过作用于截面的内力做功速率给出。在时间周t0上基于铁木辛柯梁的平均能量流〈P〉(波阵面单位长度)可描述为

(33)

在未分层区域同时存在入、反射波，由于入射波中无膨胀模态，式(33)中第3项为0，只存在两阶弯曲模态，对应正实数波数k1,k2，且须在激励频率超过截止频率时，否则k2为纯虚数时不传播能量。对应波数k1的最低基础弯曲模态，未分层区域入射波位移场为

(34)

将式(34)结合式(6)代入式(33)，得一个周期的第一阶弯曲模态平均能量流为

(35)

第二阶弯曲模态入射波可仿效式(35)获得。将k1，F1，a代替为k2，F2，b，当ω>ωc时，两列传播波同时存在，总入射波平均能量流为

(36)

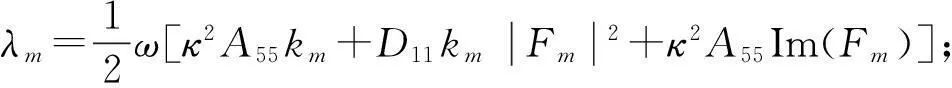
对进入未分层区域的反射波，除两阶弯曲模态亦存在一阶膨胀模态。因此，总反射波平均能量流为

(37)

式(37)中前两项系数λ1，λ2与式(36)中一致，第3项为反射的膨胀波。

在半无限大分层区域，分别考虑入射波透射进入张开、闭合分层内。张开分层时每根子梁可视为较未分层区域具有不同刚度、厚度的独立梁，因此，其透射波平均能量流可表达为

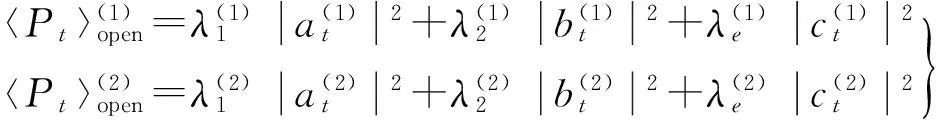
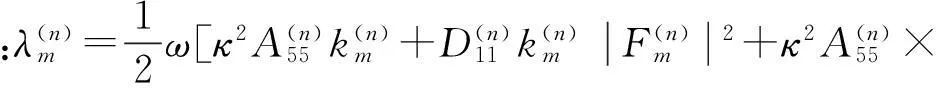
由于非传播波不传播能量，激励频率低于单根子梁截止频率(ωc1,ωc2)时，式(38)中第二项为0。在闭合分层条件下两子梁横向位移相同并耦合，且存在三阶弯曲模态，同时携带两截止频率(ωc1，ωc2)。两截止频率与张开分层条件下一致(见式(28)第1式)。对每阶传播模态，透射波平均能量流可按式(35)方法求得。而一阶膨胀模态亦存在于闭合分层区域。因此，闭合分层区域总平均能量流可写为

(39)

由于非传播波不传播能量，当激励频率低于截止频率ωc1或ωc2时式(39)第2项或第3项为0。由于反射波、透射波与入射波间通过反、透射系数矩阵联系，故选b/a=1描述两阶相同幅值入射波入射下模态转换。能量反、透射率定义为

(40)

由式(40)知，入射波在分层尖端通过反、透射后分三部分，即反射回未分层区域及透射进分层区域每根子梁中。系数均为正值，且在0～1之间，描述梁的损伤信息。

模态转换亦发生在分层梁的波动过程中，入射进分层区域能量含弯曲波及膨胀波。通过定义能量分配率，可有效描述模态转换，即

(41)

式中：分母为透射波总平均能量流；分子为进入分层区域每个模态的平均能量流；上标A0，A1，A2，S0表示不同传播模态。

该系数表示出总透射波各模态能量分配。张开分层下存在两阶弯曲模态、一阶膨胀模态，而闭合分层下有三阶弯曲模态及一阶膨胀模态，其余为A2模态。

4数值计算

本文数值计算采用IM7/5250-4石墨/环氧单向复合材料梁结构，纤维方向与梁轴线平行，横截面为矩形。IM7/5250-4材料特性见表 1。

复合材料梁未分层区域及闭合分层区域弥散关系见图2。其中分层位于h1/h=0.4处，上标0、D分别表示未分层、分层区域。由图2(a)看出，分层与未分层的A0模态在整个频域内较相近，而频率低于0.3ωc时分层后A0模态有一定下降，见图2(b)，此为分层导致弯曲刚度下降引起。此外，两A0模态均随频率趋于无限大趋向定值(κcs)。由于闭合分层区域的耦合效应，引入一阶弯曲模态(A2)，且出现两个截止频率，分层后子梁较未分层区域变薄，使两截止频率均高于未分层区的截止频率。3个截止频率将整个频域分成4个区域(图2(a))，随频率增高后两阶分层弯曲模态同未分层第二阶弯曲模态，均趋于相同定值(cl)。

表1　IM7/5250-4 材料特性

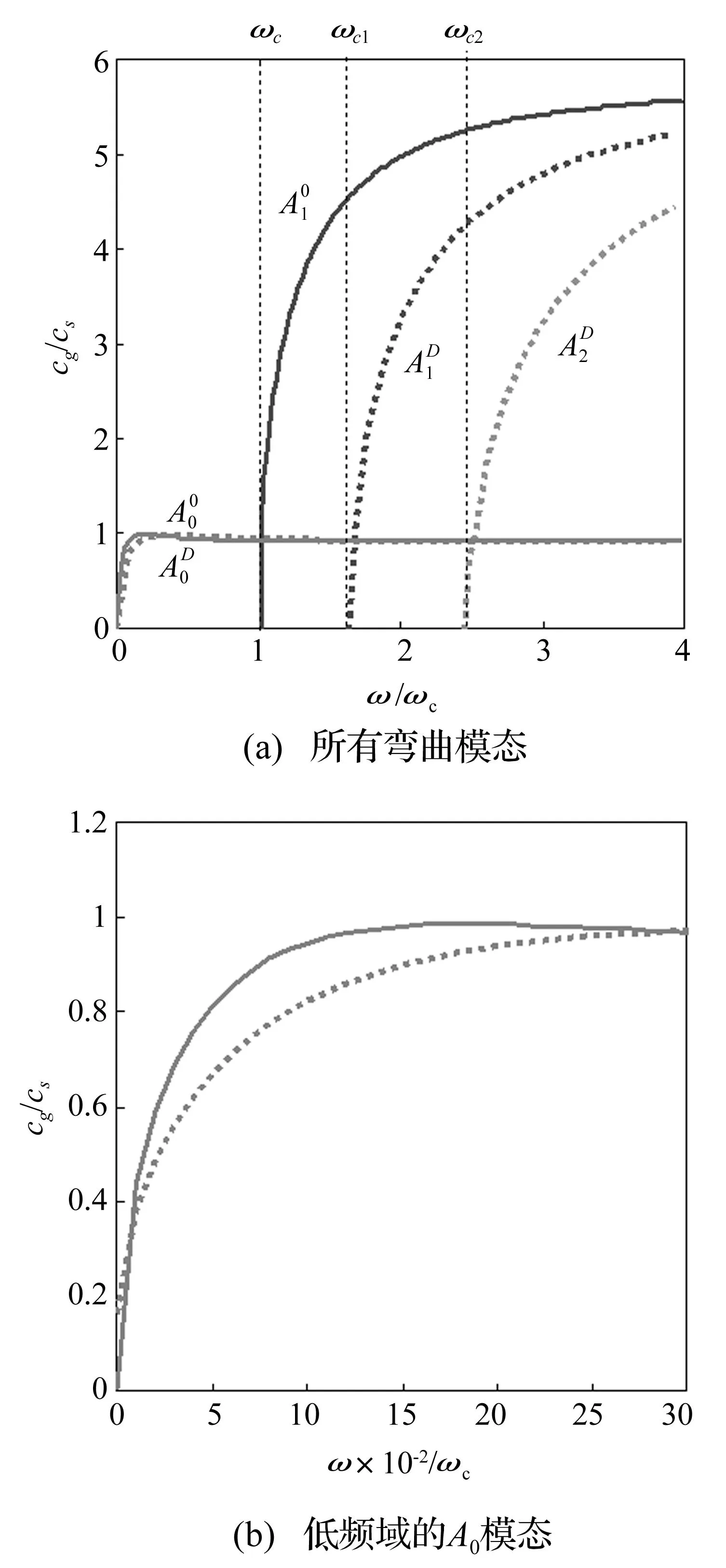
图2　弯曲模态群速度(实线为未分层区域，点线为闭合分层区域)Fig.2 The group velocities of flexural modes (solid line: un-cracked region; dotted line: closed cracked region)

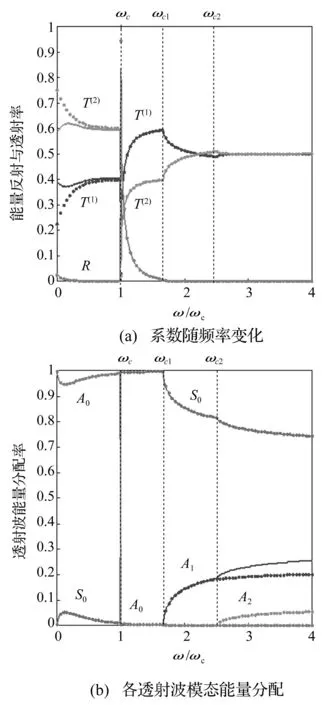
图3　分层位于h1/h=0.4处(实线为张开分层，点线为闭合分层)曲线Fig.3 Wave at h1/h=0.4(Solid line: open crack; dotted line: closed crack)

据能量反、透射系数表达式，分层位于h1/h=0.4处时系数随频率变化结果见图3(a)。数值计算表明，在整个频域内能量传输遵循守恒定律，即R+T(1)+T(2)=1。张开、闭合两种不同分层表面条件结果相近，仅在低频域内能量透射率略有不同。刚超过未分层梁的截止频率时会出现高能量反射率效应，因在该频域内传播于两子梁内的波仍未超过其截止频率，而已出现在未分层区域内第二阶弯曲模态的入射波无法转换为能传播能量的透射波，所有第二阶弯曲模态入射波均反射回去，导致此频域内高能量反射率。张开、闭合分层条件下各透射波模态能量分配见图3(b)。由图3(b)看出，频率低于未分层截止频率时A0模态为主要能量转换模态，少部分能量转换到S0模态中；频率超过ωc后膨胀模态占能量分配主要地位，此因第二阶弯曲模态引入后分层区域子梁内胀缩运动主要转换源于ψ(x,t)，其描述梁横截面关于y轴转角，导致由于分层表面缺乏轴向约束力而产生x方向强烈的胀缩运动。两阶弯曲模态随频率越过截止频率而相继出现。而在张开分层条件下并无第三阶弯曲模态，图中实线仅有A0，A1及S0模态。因此，频率超过ωc2时张开分层的A1模态携带能量等于闭合分层的A1，A2携带之和。此为两种分层条件下能量透射的唯一不同，其它频域内两种曲线吻合较好，说明分层表面条件对瞬态波传播影响不大。

固定频率下(ω=0.1ωc)能量反射率随不同分层位置变化见图4(a)。在该频率上透射波只含S0，A0两模态，膨胀波S0模态能量分配随不同分层位置变化见图4(b)。由于分层位置的对称性，图4中横坐标的取值范围为h1/h∈(0,0.5]。h1/h小于0.4时两种情况下能量反射率略有差别；h1/h接近0.5时两曲线吻合较好。此因当分层不对称时分层表面接触压力越大。相反，若分层位置越接近中面接触压力影响亦越小。尤其当出现对称分层即h1/h=0.5时中面不会有接触压力，因此两种条件下结果相同。总体而言，能量反射率随分层位置接近中面而上升，并在h1/h=0.5时达最大值，可认为由于对称分层导致分层区域弯曲刚度下降最严重。对膨胀波能量分配率曲线(图4(b))原因相同，能量分配曲线随h1/h的增加近似线性增加，亦在对称分层时达最大值。

图4　ω= 0.1ωc时随分层位置变化曲线(实线为张开分层，点线为闭合分层)Fig.4 Wave when ω= 0.1ωc (Solid line: open crack; dotted line: closed crack)

5与有限元结果比较

为验证本文提出的含半无限大分层梁中波的反、透射理论，用MSC.Partran有限元分析软件进行结构建模，模拟瞬态波在模型中的传播过程。含半无限大分层悬臂梁结构几何外形示意图见图5，其中l=150 mm，L=550 mm，h=1.8 mm。点S1位于未分层区域中面，模拟传感器测量传过该处的入射波、反射波；点S2、S3分别位于两子梁中面用于测量透射波信号。值得注意的是，由于反射的膨胀波模态几乎为0，S1仅测量弯曲模态(横向位移)，而S2、S3同时含中面处横向、轴向位移。有限元单元选平面应力4节点方型单元，单元尺寸大小取决于载波频率，须满足一个波长至少存在8个单元，以确保能准确描述波形。

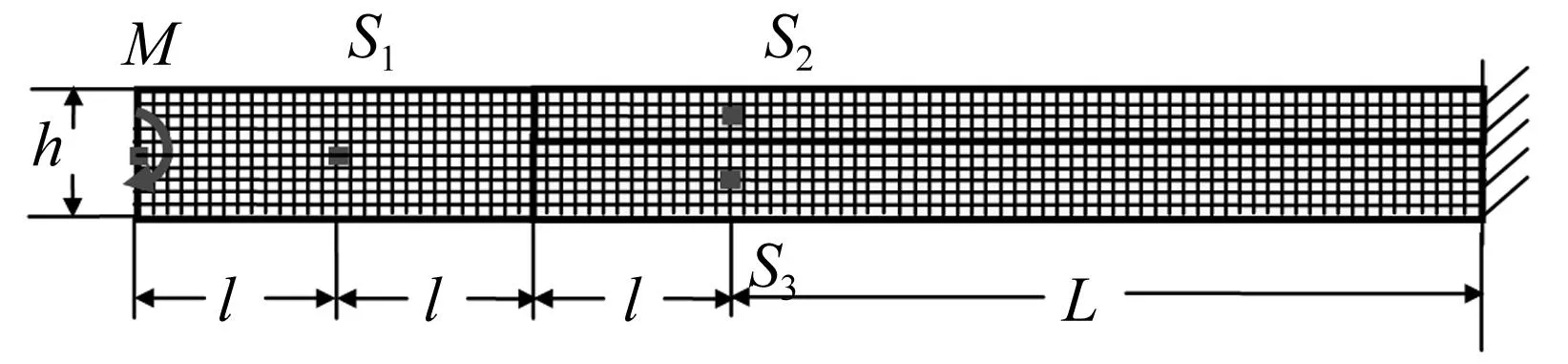
图5　分层复合材料梁有限元模型示意图Fig.5 The schematic of the beam modeled in FEM

理论分析表明，弯曲波能量流为载波频率的函数。而不可能在有限时间域内激励单频波，因此须激励多频域瞬态波信号，计算能量流时再在频域上积分。本文在悬臂梁左端中面节点激励一瞬时弯距，其函数可描述为

M(t)=M0[H(t)-H(t-5/f0)]×

(42)

此波包为加Hanning窗的5波峰窄频信号，其可保证能量集中在中心频率f0处。以50 kHz(0.1fc)为激励信号中心频率，因此只存在第一阶弯曲模态。入射波先在悬臂梁左端被激发记为a0(t)，此信号频域描述可通过傅里叶变换获得

(43)

3个模拟传感器位置采集的信号频域幅值理论上可通过将反射系数或透射系数乘以入射波频域信号获得，由于从入射点到采集点传播一定距离，故须考虑相位改变。因此理论分析的反、透射信号表达式在频域内描述为

(44)

式中：AS1(ω)为S1处频域信号，包括入、反射波信号两项。

由图5看出，入射波从激励点到S1处传播距离l，反射波到达此处则传播距离3l。而传播过程均在未分层区域，波数为k1。AS2(ω)及AS3(ω)则描述分别在S2、S3处接收的弯曲波信号，该信号先在未分层区域内传播2l距离，入射分层区域又传播距离l才到达测量点，因此相位计算须考虑两不同区域内的波数。CS2(ω)、CS3(ω)则分别代表S2、S3接收的膨胀波信号，在分层区域内传播时选择膨胀波波数。以上信号的时域表达式可通过傅里叶逆变换求得，即

(45)

式中：A(ω)代表AS1(ω)，AS2(ω)，AS3(ω)，CS2(ω)及CS3(ω)。

算例选对称分层情况，该情况描述弯曲刚度最大下降。理论分析与有限元节点处直接模拟所得信号比较见图6，可见数值计算中表面分层条件对波的反、透射影响不大，此处理论分析选张开分层与有限元结果对比。由于对称分层，S2及S3接收的信号相似，故仅给出S1、S2处结果。为方便比较，接收信号据入射信号进行无量纲化。图6(a)为S1处入、反射波的时域信号，可见理论分析与有限元结果吻合较好，且反射波峰值大约为0.1；图6(b)、(c)分别为透射的弯曲波及膨胀波信号，可见用两种方法所得信号吻合较好。而膨胀波较弯曲波更早到达S2处，此因透射波进入分层区域后距离为l的传播中，膨胀波速度大致为弯曲波速的6倍。图6(c)中出现的额外波包为因膨胀波迅速传播到悬臂梁右端边界反射回来所致。

由于存在弥散现象，瞬态波能量流计算需考虑各频域分量积分。总平均能量流可写为

(46)

式中：λ(ω)为随频率变化的单频能量流系数；A(ω)为横向位移瞬态波幅值频谱描述。

瞬态波能量反、透射率计算可通过理论分析结果结合积分式(46)获得。由于有限元模型基于梁的弹性理论建立，与铁木辛柯梁理论有所不同，其平均能量流表达式可描述为

(47)

式中：σx为应力；τxz为位移u，w及坐标x，z，t的函数。

为计算流过截面y-z的能量，x可取作常量x0，由于本文基于平面应力条件，此变量可通过在z方向取所有有限元节点值积分获得。式(46)、(47)给出两种计算平均能量方法后，在给定中心频率0.1fc处能量反射率及膨胀波能量分配率随分层位置变化见图7。由图7看出，有限元仿真结果与理论分析非常接近。在中心频率下能量反射率在对称分层处达最大值0.011 5，而膨胀波能量分配率达最大值0.055 6。两条曲线均近似随分层位置线性变化，分层在厚度方向的位置变化可作为分层损伤位置识别的有效参数。

图6　有限元节点处接收的位移信号与理论分析结果比较 Fig.6 The signals received from the FEM nodes compared with analytical results

图7　ω=0.1ωc时有限元与理论分析结果比较Fig.7 Comparison of finite element and theoretical analysis results for ω=0.1ωc

6结论

通过研究瞬态波在含半无限大分层复合材料梁的反、透射现象，分别考虑两种极端分层即张开、闭合分层，导出反、透射系数矩阵及能量反、透射率以及透射波能量分配率，分析模态转换。结论如下：

(1)分层表面条件对瞬态波传播影响不大，反、透射系数矩阵随频率及分层位置变化而变化。

(2)能量传输在整个频域内遵循守恒定律，能量反射率及膨胀波能量分配率随分层位置近似呈线性变化，并在对称分层时达最大值。

参 考 文 献

[1] Wang J T S, Lou Y Y, Gibby J A. Vibration of split beams[J].Journal of Sound and Vibration,1982,84(4):491-502.

[2] Mujumdar P M, Suryanarayan S. Flexural vibrations of beams with delaminations[J].Journal of Sound and Vibration,1988,125(3):441-461.

[3] Rosalie S C, Vaughan M, Bremner A,et al.Variation in group velocity of Lamb waves as a tool for the detection of delamination in GLARE aluminum plate-like structures[J].Composite Structures,2004,66(1/2/3/4):77-86.

[4] Yan Y J,Yam L H.Detection of delamination damage in composite plates using energy spectrum of structural dynamic responses decomposed by wavelet analysis[J].Computers and Structures, 2004,82(4/5):347-358.

[5] Farris T N, Doyle J F. Wave propagation in a split Timoshenko beam[J].Journal of Sound and Vibration,1989,130(1): 137-147.

[6] Hayashi T, Kawashima K. Multiple reflections of Lamb waves at a delamination[J].Ultrasonics, 2002,40(1/2/3/4/5/6/7/8):193-197.

[7] Ostachowicz W, Krawczuk M, Cartmell M,et al.Wave propagation in delaminated beam[J].Computers and Structures,2004,82(6):475-483.

[8] Lase Y,Ichchou M N,Jezequel L. Energy flow analysis of bars and beams: theoretical formulations[J].Journal of Sound and Vibration, 1996,192:281-305.

[9] Pan J, Ming R,Hansen C H,et al.Experimental determination of total vibratory power transmission in an elastic beam[J]. Journal of Acoustic Society of America, 1998,104(2):898-906.

[10] Bazer J, Burridge R. Energy partition in the reflection and refraction of plane waves[J].SIAM Journal of Applied Mathematics,1978,34(1):78-92.

[11] Wang C H, Rose L R F. Wave reflection and transmission in beams containing delamination and inhomogeneity[J].Journal of Sound and Vibration, 2003,264(4):851-872.

Wave reflection and transmission in composite beams

FENGYong-ming1,2,ZHOULi2,YANGJian-yuan1,YUANWan-chun2

(1. Beijing Aeronautical Technology Research Center, Beijing 100076, China；2. State Key Laboratory of Mechanics and Control of Mechanical Structures，Nanjing University of Aeronautics and astronautics，Nanjing 210016, China)

Abstract:The wave reflection and transmission in composite beams containing a semi-infinite delamination were studied analytically based on the Timoshenko beam theory. Two extreme cases of delaminated surface conditions, non-contact(open) and full contact(closed) delaminations, were considered respectively for a unidirectional composite beam. The analytical solution of reflection and transmission matrices for a semi-infinite delamination was derived. Then the power reflection and transmission coefficients were obtained, which depend on both the wave frequency and the location of the delamination. The numerical results show the conservation of power transport. The power distribution was also investigated to describe the mode conversion between two flexural modes and one extensional mode. A finite element simulation was used to verify the validity of the analytical results.

Key words:delamination; reflection and transmission; composite beam; power transport

中图分类号:V257

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.06.004

通信作者周丽 女，博士,教授,博士生导师,1963年生

收稿日期：2014-12-21修改稿收到日期：2015-03-23

基金项目：机械结构力学及控制国家重点实验室开放课题(MCMS-0513G02)

第一作者 冯勇明 男，博士,工程师,1983年生