超长柔性臂架回转振动主动控制研究

黄　毅， 鄂加强， 郭　岗, 唐闽艳， 胡　伟

(1. 湖南大学 汽车车身先进设计制造国家重点实验室，长沙　410013；2.中联重科股份有限公司 国家混凝土机械工程技术研究中心，长沙　410013; 3. 国网长沙县供电公司，长沙　410100)



超长柔性臂架回转振动主动控制研究

黄毅1,2， 鄂加强1， 郭岗2, 唐闽艳3， 胡伟2

(1. 湖南大学 汽车车身先进设计制造国家重点实验室，长沙410013；2.中联重科股份有限公司 国家混凝土机械工程技术研究中心，长沙410013; 3. 国网长沙县供电公司，长沙410100)

摘要：针对超长柔性臂架回转振动过大问题，结合臂架结构特点基于有限单元法建立臂架回转动力学模型，分析臂架回转系统振动特性。采用模态滤波技术及最优极点配置算法进行主动控制策略设计与理论分析，并搭建主动控制试验系统，进行超长臂架回转振动主动控制试验。试验结果表明，该振动主动控制方法能有效提升受控系统阻尼比(增幅920%)，显著抑制臂架回转振动衰减时间(减幅73%)，振动控制效果明显，不仅对研制更长臂架泵车具有重要的理论及应用价值，且对所有具有超长柔性机械臂高端装备回转振动控制具有重要参考价值。

关键词：柔性臂架；回转振动；振动主动控制；模态滤波；极点配置

泵车作为连续、作业高效、浇筑灵活、转运方便的混凝土施工装备广泛用于工程建设。尤其大型建设中，大于60 m的超长臂架泵车因施工范围广，为高质量工程提供重要保障。目前，世界最长泵车臂架已达到101 m。而臂架的增长致臂架柔性急剧增大，在回转制动惯性力、混凝土换向冲击力的复杂冲击作用下极易引起较大回转方向振动，会严重影响臂架的定位精度、疲劳寿命及施工安全，因而制约超长臂架泵车的推广及应用。

传统振动被动控制由于重量增加、低频效果差等限制在超长臂架的应用，而主动控制因减振效果好、功耗低、适应性强等成为抑制超长臂架振动的有效手段[1]。文献[2]利用压电作动器与关节力矩控制结合方法实现对柔性机械臂回转振动的主动控制。文献[3]采用极点配置法对泵送条件下臂架垂向振动进行试验研究。文献[4]利用神经网络及模糊PD对大柔性机械臂末端进行控制研究。文献[5]利用自适应控制方法驱动滚珠丝杠机构控制柔性机械臂的非线性振动，取得良好效果。文献[6]采用H∞结合PID控制研究单连杆柔性机械臂的鲁棒控制。文献[7]则提出遗传算法与模糊控制相结合的双连杆柔性臂控制方法。文献[8]采用预测控制结合I/O反馈线性化的控制策略，消除柔性机械臂弹性振动。文献[9]针对起重机系统中由旋臂旋转产生的二维荷载摆角问题提出只基于旋臂旋转的控制方式同时实现旋臂位置控制及载荷消摆控制。因此，在柔性臂架振动主动控制方面对垂向振动研究较多，对回转振动研究较少。

本文以ZLZK-80RZ超长臂架泵车为研究对象，建立臂架系统回转动力学模型，分析动态特性，采用模态滤波技术及最优极点配置算法进行主动控制策略设计。通过控制系统及液压作动系统方案设计与实物搭建，实现柔性臂架回转振动主动控制方法的试验验证。

1未控系统动态特性分析

泵车臂架回转机构主要由回转液压马达、回转减速机、回转台、臂架等组成。回转液压马达的转动通过回转减速机驱动回转台转动，实现与回转台联接的臂架回转运动。在臂架回转系统动力学建模及特性分析中，考虑控制器计算成本及控制自身的复杂程度，据每段臂节结构特点，将其离散成若干梁单元简化处理，见图1。

图1臂节离散示意图
Fig.1 Discrete model of boom

通过有限单元法进行装配，获得臂架回转系统动力学模型总体质量矩阵M、刚度矩阵K及阻尼矩阵C，进而据动力学理论获取系统动态特性参数。各臂节主要结构参数见表1。

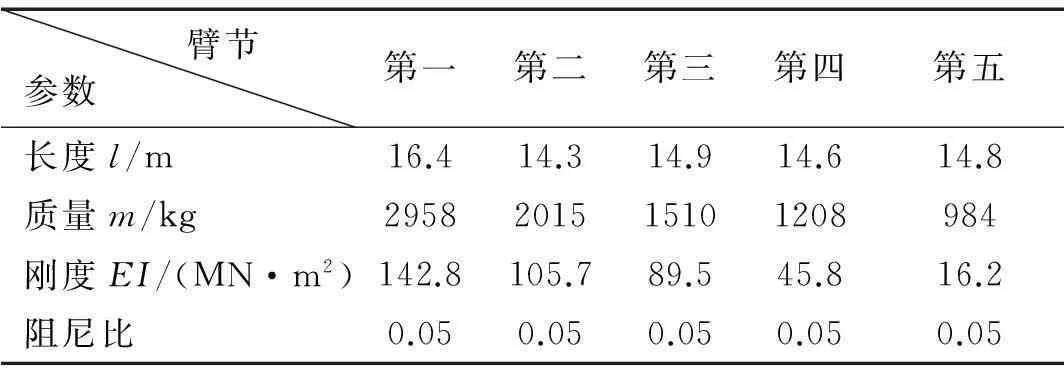
表1　臂节结构参数表

基于Matlab平台，采用臂节离散化处理计算获得未控臂架系统各阶模态参数，其中振型及极点分布图见图2、图3。臂架第一阶振型表现为一阶弯曲，模态频率0.22 Hz，模态阻尼比0.031。第二阶振型表现为二阶弯曲，模态频率0.66 Hz，模态阻尼比0.26。由图3可知，未控系统第一、二阶模态对应极点分别为λ1,2、λ3,4，其中λ1,2=-0.043±1.38j，λ3,4=-1.08±4.01j。未控臂架系统第一阶模态对应阻尼比0.031，由于该阻尼比过小，实际中由回转制动惯性力、混凝土换向冲击力的复杂冲击作用导致臂架回转方向振动会持时较长，较难快速衰减。考虑工程中臂节回转振动主要以一阶振动为主，较难激发二阶以上的模态振动，因此控制系统以增大臂架一阶回转振动阻尼为目标，暂不对其它高阶模态施加控制。

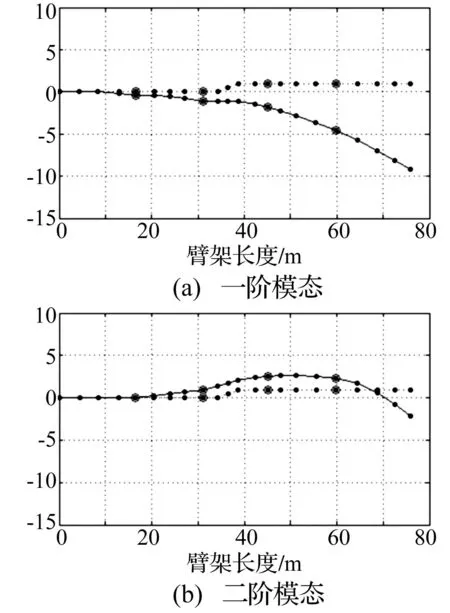
图2　臂架模态振型图Fig.2 Modal shape of boom

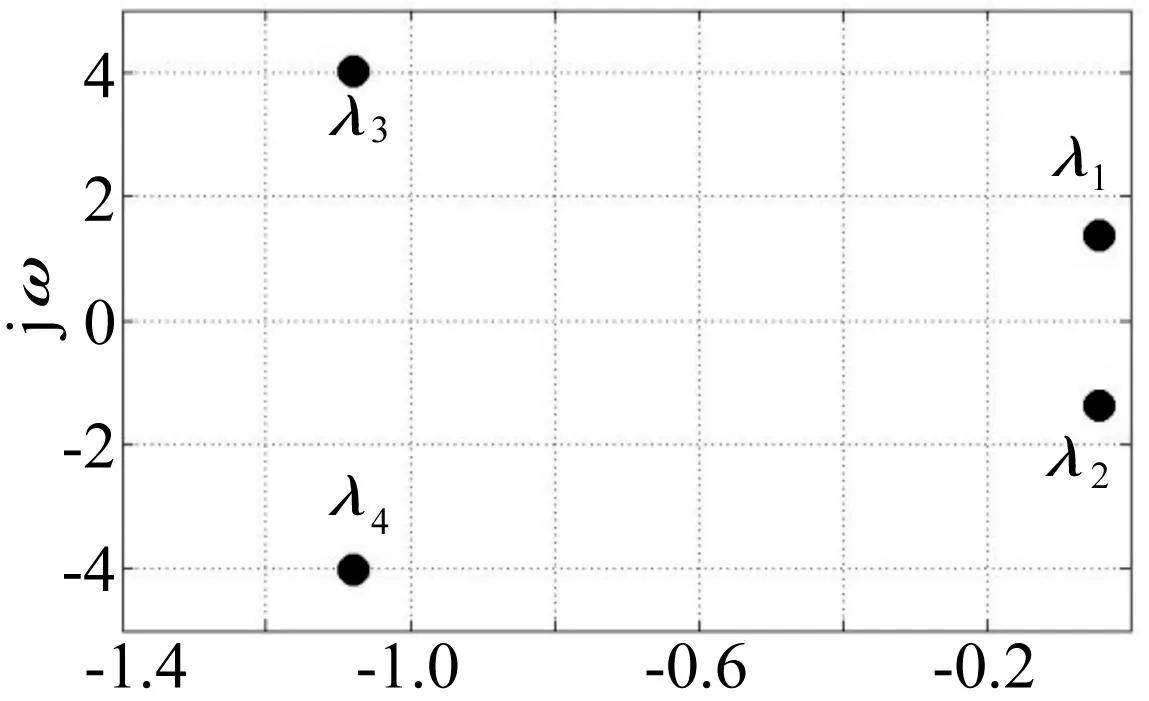
σ图3　未控系统极点分布图Fig.3 Pole distribution of uncontrolled system

2主动控制方案设计

2.1控制策略设计

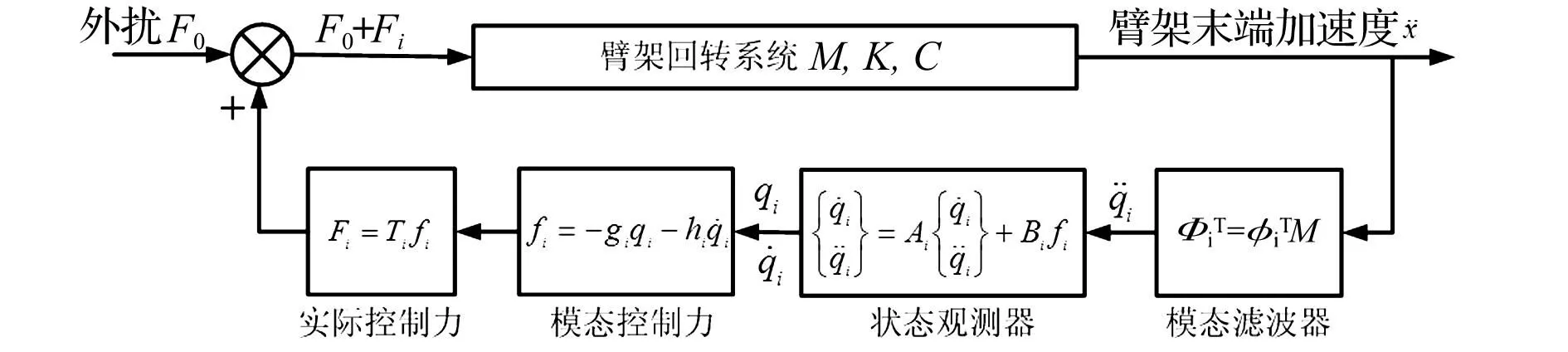
图4　控制方法框图Fig.4 Principle diagram of control method

据模态理论，臂架振动响应x可由前几阶主模态近似表示为

(1)

独立模态空间控制法可在不影响其它未控模态条件下实现对所需控制模态的独立控制，但需同时获知模态位移及速度。由于臂架回转振动伴随大范围空间运动出现，难以获取回转振动位移或速度信号，一般获取回转振动加速度信号。因此，通过引入模态滤波器实现从物理加速度转换获得模态加速度，进而通过引入状态观测器实现从模态加速度到模态速度、位移的转换。

(2)

对控制的第i阶回转模态，其模态控制力为

(3)

模态控制力增益系数gi及hi通常由极点配置法确定，若要求第i阶模态极点配置在λi=αi±βij处，则可由闭环特征方程求得，即

(4)

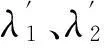
σ图5　受控系统极点分布图Fig.5 Pole distribution of controlled system

对独立模态空间控制算法而言，振动系统各阶模态均相互独立，故获得实际控制力为

(5)

2.2控制系统实现

考虑控制的实时性与可靠性，系统用美国NI公司LabVIEW开发环境及CompactRIO嵌入式控制器实现。系统控制方案见图6，CRIO 9014控制器通过NI9862高速CAN模块监测包括泵送开关、减振开关、泵送排量等泵车状态信号；通过NI9233加速度模块实时采集臂架末端横向加速度信号，分析臂架回转振动烈度，并据控制策略计算主动控制变量；通过NI9205应变模块监测臂架结构关键点动应力信号；经NI9401数字模块输出PWM形式控制信号到功率放大器驱动液压作动器给受控对象施加主动控制力。

液压作动器由伺服电磁阀、回转液压马达、回转减速机等组成。伺服电磁阀通过调整阀芯位置控制液压油流向、流速，从而控制回转液压马达的正反转及转速。回转液压马达往复转动通过回转减速机驱动回转台往复转动，实现主动控制作用输出。

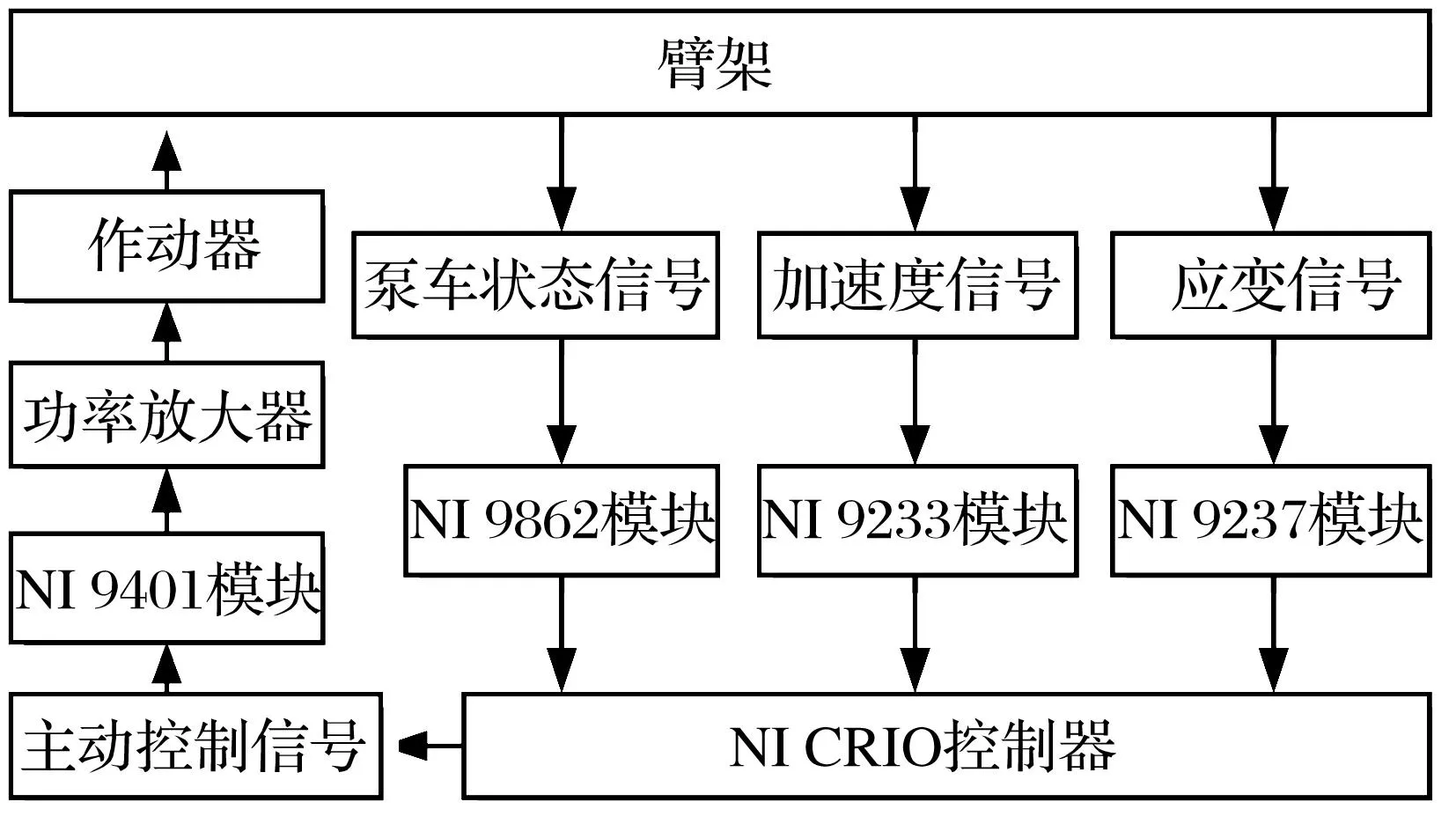
图6　系统控制硬件结构图Fig.6 Block Diagram of control hardware

3试验验证与分析

为验证振动主动控制方案的有效性，选中联重科ZLZK-80RZ超长臂架泵车，实施臂架回转振动主动控制试验，选泵车回转机构作为臂架回转振动主动控制作动器，控制器CRIO 9014安装于泵车侧面电控柜内，控制循环为50 ms，在第5臂架末端侧面相互垂直安装2个加速度传感器测量臂架末端振动，传感器型号PCB393B04，灵敏度1 000 mV/g。在第3臂侧面沿轴线方向粘贴电阻120 Ω的应变片测量臂架应力变化。实验现场见图7。

图7　试验现场图Fig.7 Experiment of active vibration control

考虑极端工况，此时约75 m的超长臂架接近水平姿态，且以泵水模拟实际施工中泵送混凝土介质。泵车试验参数为泵送排量70%、发动机转速1 750 r/min，混凝土输送缸的泵送频率达0.28 Hz，较接近一阶回转模态频率。此时臂架横向柔度最大，模拟实际施工中出现的臂架断续回转运动时回转制动惯性力及泵送换向冲击力的复杂冲击作用导致明显回转振动，振动控制难度亦最大。

试验分不施加控制、施加控制进行减振效果对比，其中不施加控制即采用斜坡延时技术，而施加控制即采用本文的振动主动控制技术。初始条件均以最大回转速度操作臂架回转，达稳态速度时突然停止回转操作，实时采集安装于臂架末端的拉线传感器信号及臂架结构某关键点的应变片信号，用于对减振效果评价。结果见图8、图9。对比未控、受控的臂架末端回转位移时间历程曲线可知，施加振动主动控制后的臂架回转振动得到有效抑制，系统阻尼比由0.031提高到0.287，增幅约920%；衰减时间(本文定义为从振动开始到振幅衰减至125 mm以内所用时间)由48 s缩短至13 s，减幅73%；对比未控、受控臂架关键点应力时间历程可知，施加振动主动控制后臂架关键点应力幅值明显衰减，衰减率约33%。

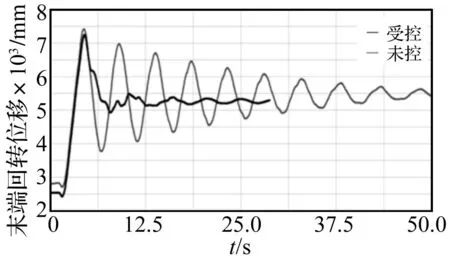
图8　臂架末端回转位移时间历程Fig.8 Slewing displacement of boom tip

图9　臂架关键点应力时间历程Fig.9 Stress amplitude of boom

4结论

(1)针对目前超长臂架泵车应用中存在的回转振动过大等瓶颈问题，结合臂架结构特点基于有限单元法建立臂架回转动力学模型，分析臂架回转系统动态特性，采用模态滤波技术及最优极点配置算法进行主动控制策略设计与理论分析，并搭建主动控制试验软硬件系统，成功应用于ZLZK-80RZ超长臂架泵车的振动主动控制试验。

(2)采用主动控制策略后，臂架系统阻尼比由0.031提高到0.287，增幅约920%；臂架末端回转振动位移幅值衰减时间由48 s缩短至13 s，减幅73%；臂架关键点应力幅值衰减率约33%。

参 考 文 献

[1] 欧进萍. 结构振动控制-主动、半主动和智能控制[M]. 北京: 科学出版社, 2003.

[2] 韩清鹏,于晓光,唐玲. 一种柔性机械臂旋转运动和振动的主动控制方法[J]. 机械科学与技术,2012,31(4)：685-688.

HAN Qing-peng, YU Xiao-guang,TANG Ling. An active control method for vibration and rotary motion of flexible manipulator[J]. Mechanical Science and Technology, 2012, 31(4)：685-688.

[3] 黄毅,郭岗,邝昊,等. 混凝土泵车臂架回转系统动力学分析及预测[J]. 机械强度,2014, 36(2): 300-304.

HUANG Yi, GUO Gang, KUANG Hao,et al. Dynamics analysis and prediction on boom slewing system of the concrete pump truck[J].Journal of Mechanical Strength,2014,36(2): 300-304.

[4] Mohamed I, Matrins J M. Vibration control of a very flexible manipulator system[J]. Control Engineering Practice, 2005, 13(3):267-277.

[5] Qiu Zhi-cheng. Adaptive nonlinear vibration control of a cartesian flexible manipulator driven by a ballscrew mechanism[J]. Mechanical Systems and Signal Processing, 2012, 30: 248-266.

[6] Ho M T, Tu Y W. Position control of a single-link flexible manipulator using H∞-based PID control[J]. Control Theory and Applications, 2006, 153(5): 615-622.

[7] Nguyen V B, Morris A S. Using a genetic algorithm to fully optimise a fuzzy logic controller for a two-link-flexible robot arm[J]. Robotic, 2009, 27(5):677-687.

[8] 帅鑫,李艳君,吴铁军. 一种柔性机械臂末端轨迹跟踪的预测控制算法[J]. 浙江大学学报, 2010, 44(2):259-263.

SHUAI Xin, LI Yan-jun, WU Tie-jun. Realtime predictive control algorithm for endpoint trajectory tracking of flexible manipulator[J]. Journal of Zhejiang University,2010,44(2): 259-263.

[9] 欧阳慧珉,内山直树,佐野滋则,等.只利用旋臂旋转运动的起重机消摆控制[J].振动与冲击,2014,33(4):131-137.

OUYANG Hui-min,UCHIYAMA Naoki,SANO Shigenori, et al. Load sway suppression control for rotary cranes using only horizontal boom motion[J].Journal of Vibration and Shock,2014,33(4):131-137.

Active control of slewing vibration in an ultra-long flexible boom

HUANGYi1,2,EJia-qiang1,GUOGang2,TANGMin-yan3,HUWei2

(1.The State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body, Hunan University， Changsha 410013，China;2.National Engineering Research Center for Concrete Machinery，Zoomlion Heavy Industry Science & Technology Co.，Ltd.，Changsha 410013，China;3. State Grid Changsha Power Supply Company, Changsha 410100, China)

Abstract:In order to address severe slewing vibration in ultra-long flexible booms，the mechanism identification and active control of the slewing vibration were considered. Firstly，a simplified dynamical model of a slewing boom system was built according to the finite element method，and the slewing characteristics of the model were analyzed. Secondly，the active vibration control method was presented, which combines the algorithms of modal filtering and optimal pole assignment. Finally，the test platform based on NI instrumentation was implemented and the active vibration control experiment was carried out. The experimental results showed that the damping ratio of the controlled slewing system increases and the slewing vibration of the boom tip obviously decreases，which validates the effectiveness of the proposed method.

Key words:flexible boom; slewing vibration; active vibration control; modal filtering; pole assignment

中图分类号:TB535

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.06.025

收稿日期：2015-06-10修改稿收到日期：2015-09-28

基金项目：国家自然科学基金(51305045)；中国博士后科学基金(2014M562099)

第一作者 黄毅 男，博士后，高级工程师，1978年3月生

E-mail：tjhuangyi110@163.com