中厚椭球壳自由振动动力刚度法分析

陈旭东， 叶康生

(1.江苏科技大学 船舶与建筑工程学院，江苏 张家港　215600；2. 清华大学 土木工程系 土木工程安全与耐久教育部重点实验室，北京　100084)



中厚椭球壳自由振动动力刚度法分析

陈旭东1， 叶康生2

(1.江苏科技大学 船舶与建筑工程学院，江苏 张家港215600；2. 清华大学 土木工程系 土木工程安全与耐久教育部重点实验室，北京100084)

摘要：介绍精确动力刚度法分析中厚椭球壳自由振动具体实施方法，据环向波数不同将中厚椭球壳自由振动分解为一系列确定环向波数的一维振动；利用控制方程Hamilton形式建立动力刚度关系，用常微分方程求解器COLSYS求解控制方程获得单元动力刚度，用Wittrick-Williams算法求得该环向波数下椭球壳自振频率。数值算例给出中厚圆球壳及椭球壳不同边界条件的自振频率，验证动力刚度法高效、可靠、精确。

关键词：椭球壳；自由振动；动力刚度法；Wittrick-Williams算法；Hamilton形式

椭球壳广泛用于土木工程、化工、机械、航空航天等重要行业。准确求解椭球壳的自由振动，可为进一步动力分析提供基本参数，具有重要理论意义及工程价值。Lamb[1]最早分析椭球壳自由振动，DiMaggio等[2-5]对扁平及长椭球壳自由振动进行研究。以上分析均基于薄壳理论。对较厚壳体，应考虑剪切变形及转动惯量影响。Sai Ram等[6]基于一阶剪切变形理论采用有限元法计算复合材料球壳的自振频率；Hosseini-Hashemi等[7]用辅助势函数及分离变量法获得球壳面板自由振动解析解；Su等[8]用傅里叶级数及Rayleigh-Ritz法分析中厚分段球壳的自由振动；Kang等[9-10]用三维理论结合Ritz法求解变厚度球壳的自由振动。

本文视结构为无限自由度分布参数体系，将控制方程降阶后用常微分方程求解器COLSYS[11-12]获得精确动力刚度，用Wittrick-Williams算法[13-14](W-W算法)对频率计数，求得结构自振频率。

动力刚度法因分析精确，多用于杆系结构自由振动问题[15-17]。在板壳领域，El-Kaabazi等[18]将动力刚度法用于轴对称薄圆柱壳自由振动分析。本文从考虑横向剪切变形及转动惯量的中厚壳理论出发，推导中厚椭球壳自由振动控制方程与动力刚度关系，该方法可直接用于双曲壳、抛物壳等旋转壳的自由振动求解。

1基本方程

图1　椭球壳子午线及坐标系示意图Fig.1 Diagram of an elliptical shell meridian and coordinates

椭球壳见图1，设u，v，w分别为椭球壳中面某点沿子午线方向、环向及法向的线位移；φ为该点法线与对称轴z的夹角；θ为纬圆环向；E为椭球壳弹性模量；ν为泊松比；ρ为密度；h为厚度，沿环向封闭。在OXZ平面内，子午线方程为

(1)

据中厚壳理论，椭球壳中面应变与位移关系为

{ε}=[L]{Δ}

(2)

式中：{ε}={εφ,εθ,εφθ,χφ,χθ,χφθ,γφ,γθ}T为应变向量；{Δ}={u,v,w,ψφ,ψθ}T为位移向量；ψφ，ψθ分别为中面沿φ、θ方向角位移；[L]为微分算子矩阵，即

类似，椭球壳内力、中面应变关系为

{N}=[D]{ε}

(4)

式中： {N}={Nφ,Nθ,Nφθ,Mφ,Mθ,Mφθ,Qφ,Qθ}T为内力向量；[D]为刚度矩阵，即

(5)

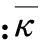
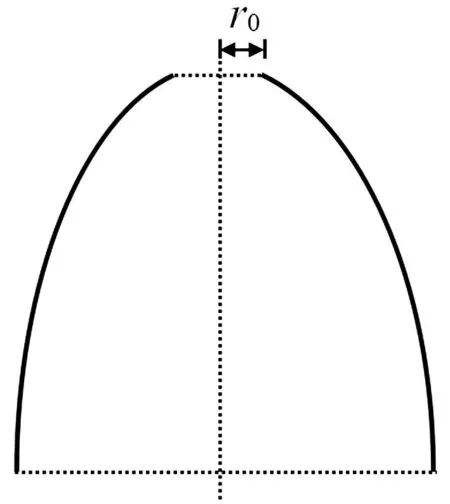
图2　椭球壳横断面及顶点开口r0Fig.2 Transverse section of an ellipsoidal shell and opening r0 at apex

由于微分算子L中出现1/r项，对完全椭球壳，在子午线顶点因r=0会造成L矩阵奇异。本文在顶点开小圆孔，即在子午线顶点开半径为r0圆孔，见图2，r0非常小时可认为椭球壳在顶点接近封闭。

2自由振动对偶系

在椭球壳上截取一微元，据几何关系，此微元面积为dA=rRdθdφ。将微元应变能在整个中面S上积分，得椭球壳自由振动应变能为

(6)

椭球壳自由振动动能为

(7)

由Hamilton原理

(8)

可推出壳体自由振动运动方程。取动位移函数为

(9)

式中：n为环向波数；ω为自振圆频率；un(φ)，vn(φ)，wn(φ)，ψφn(φ)，ψθn(φ)为子午向振型函数。

将该动位移函数代入运动方程，可得中厚壳自由振动控制方程，写成Hamilton形式为

[J]{z′}=[S]{z}

(10)

式中：( )′为对φ求导。

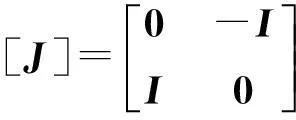
(11)

式中：I为5阶单位矩阵；{z}为状态向量，由环向波数n下振型对偶量(位移、内力)组成，即

{z}={q1q2q3q4q5p1p2p3p4p5}T

(12)

式中：内力量为

(13)

位移量为

q1=un,q2=vn,q3=wn,q4=ψφn,q5=ψθn

(14)

式(10)中[S]为10阶对称矩阵，记sij为元素，则其中上三角非零元素分别为

(15)

3动力刚度

图3　椭球壳沿子午线方向壳段划分Fig.3 The mesh division along the meridian

对式(10)中控制方程，据位移量及内力量，类似杆件理论建立椭球壳自由振动动力刚度关系。由于方程的复杂性，式(10)用常微分方程求解器COLSYS进行数值求解。取椭球壳曲率半径与z轴夹角φ为基本坐标，并按φ将椭球壳沿子午线划分成ne个壳段单元，见图3。

以单元(e)为例，设两端φ坐标为φa、φb，单元端位移向量{d}e及力向量{F}e与位移、内力函数间关系为

{d}e={q1(φa),q2(φa),q3(φa),q4(φa),q5(φa),

q1(φb),q2(φb),q3(φb),q4(φb),q5(φb)}T

{F}e={-p1(φa),-p2(φa),

-p3(φa),-p4(φa),-p5(φa),

p1(φb),p2(φb),p3(φb),p4(φb),p5(φb)}T

(16)

据刚度定义，求解式(10)时对单元端部节点位移向量依次取10个不同单位向量，即对式(10)依次施加边界条件为

{d}e={ej},(j=1,…,10)

(17)

式中：{ej}为第j元素单位值单位向量。

解得此时单元端部节点力向量，依次排列则得椭球壳壳段单元动力刚度矩阵，即

(18)

将所有壳段单元动力刚度阵按常规有限元集成，即可获得椭球壳自由振动的整体动力刚度矩阵K。

4Wittrick-Williams算法

W-W算法认为结构所有频率中低于给定值ω*的频率个数为

J=J0+s{K(ω*)}

(19)

式中：J0为低于ω*的单元固端频率总数；s{ }为负数计数；s{K(ω*)}为用高斯消去法将整体动力刚度矩阵K(ω*)消成上三角矩阵后(不换行)主对角线上负元素个数。

(20)

(21)

图4　COLSYS对壳段单元(e)内部子区间划分Fig.4 The sub-mesh division of COLSYS on element (e)

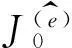
(22)

(23)

式中：

(24)

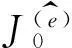
(25)

5数值算例

通过3个算例验证本文方法的正确性。

5.1算例1

一端固定一端自由球壳段自由振动。令子午线方程(1)中a=b，则椭球壳退化为标准球壳。Gautham等[19]用有限元方法分析顶点有30°、60°截断开口的中厚半球壳自由振动，边界条件为下端固定、上端自由，见图5。

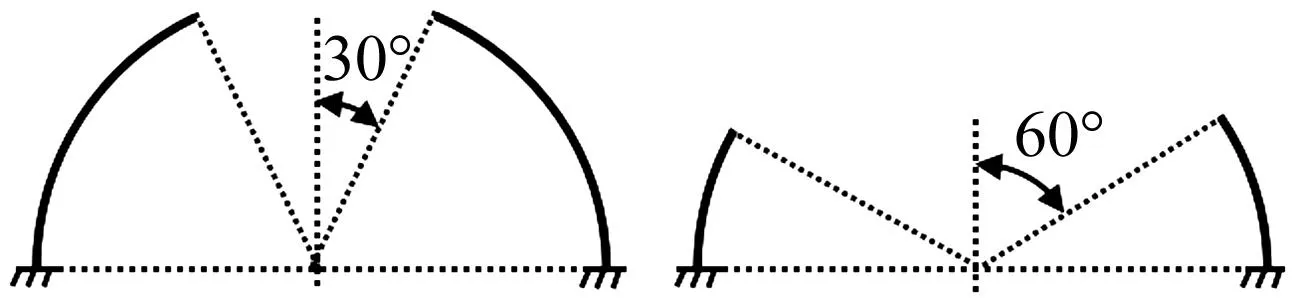
图5　截断开口球壳示意图Fig.5 Diagram of hemi-spherical caps with cutout

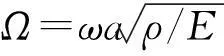
5.2算例2

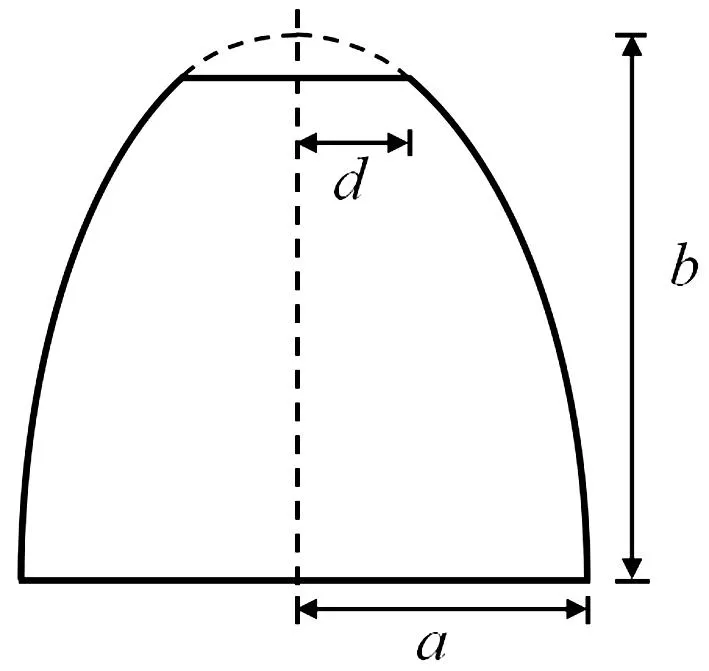
图6　两端自由椭球壳示意图Fig.6 Diagram of a free-free ellipsoidal shell

表1　30°开口半圆球壳的频率参量Ω

表2　60°开口半圆球壳的振动频率参量Ω

表3　b/a=1/2时两端自由椭球壳自振频率Ω

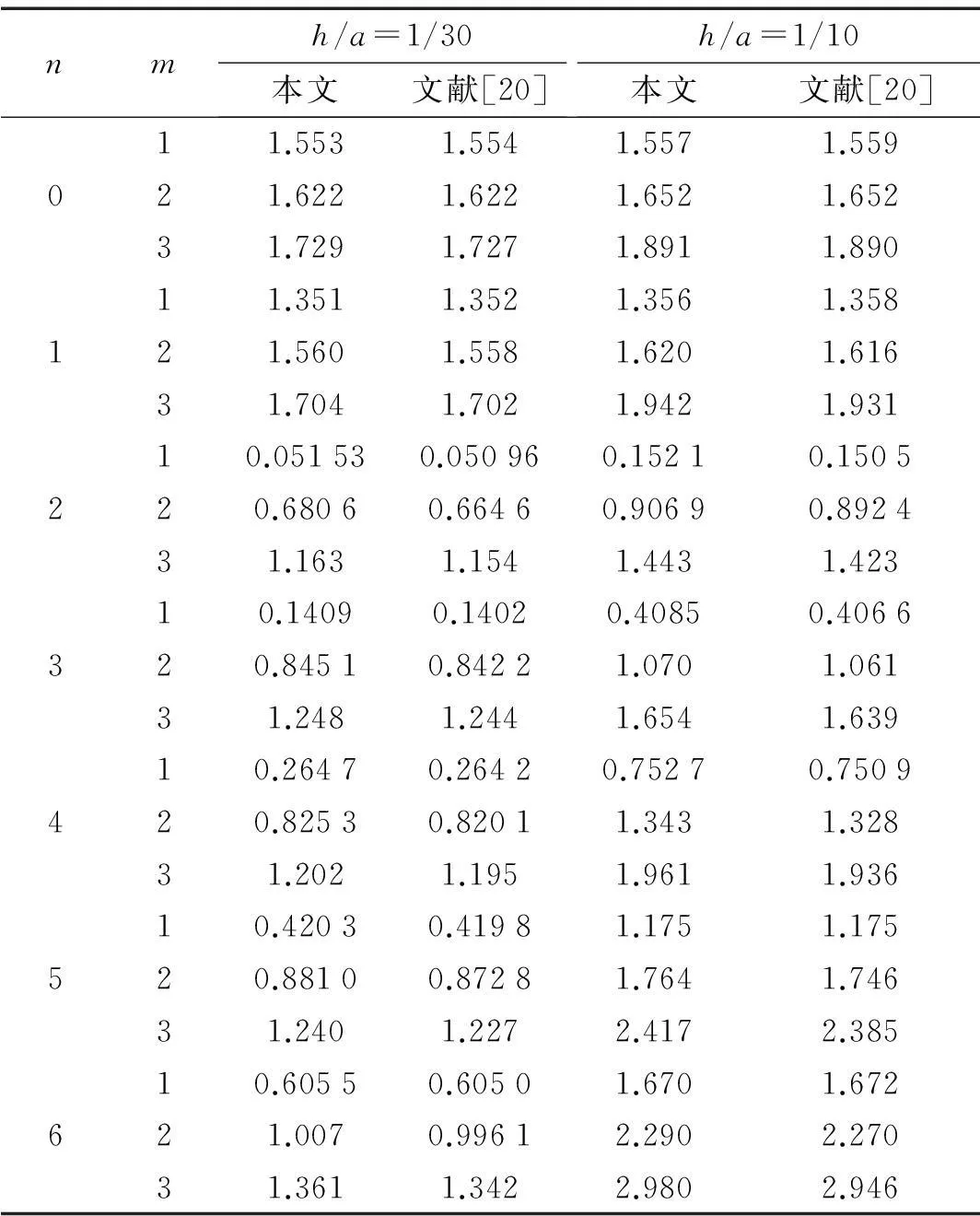
表4　b/a=2时两端自由椭球壳自振频率Ω

5.3算例3

顶点封闭半椭球壳自由振动。文献[20]用三维弹性理论结合Ritz法对上顶点封闭、下端自由的半椭球壳进行分析，壳体参数为b/a=3，h/a=1/10，泊松比ν=0.3。为避免顶点几何算子中1/r的奇异性，开小口，开口大小为r0/a=10-5。本文亦用开小口方法避免顶点处奇异性，开口大小同文献[20]。用本文方法与文献[20]的三维弹性Ritz法所求半椭球壳在不同环向波n下的最小非零频率参量Ω(表达式同例2)见表5，可见吻合很好。

表5　半椭球壳的自振频率Ω

6结论

阐述应用动力刚度法分析中厚椭球壳自由振动过程，据结构的轴对称性，将椭球壳自由振动问题降为一维自由振动问题，由一维问题的内力量、位移量建立单元动力刚度关系，用COLSYS求解动力刚度关系满足的常微分方程边值问题，获得单元动力刚度。并用W-W算法获得结构频率。

本文方法通用性强，可直接推广至其它轴对称旋转壳(如双曲壳、抛物壳等)的自由振动分析。

参 考 文 献

[1] Lamb H. On the vibration of a spherical shell[J]. Proceedings of the London Mathematical Society, 1883, 14: 50-56.

[2] DiMaggio F L, Silbiger A. Free extensional torsional vibrations of a prolate spheroidal shell[J]. Journal of Acoustical Society of America, 1961, 33(1): 56-58.

[3] Penzes L E, Burgin G. Free vibration of thin isotropic oblate-spheroidal shells[J]. Journal of Acoustical Society of America, 1966, 39(1): 8-13.

[4] Niordson F I. Free vibrations of thin elastic spherical shells[J].International Journal of Solids and Structures,1984,20(7):667-687.

[5] Al-Jumaily A M, Najim F M. An approximation to the vibrations of oblate spheroidal shells[J]. Journal of Sound and Vibration, 1997, 204(4): 561-574.

[6] Sai Ram K S, Sreedhar Babu T. Free vibration of composite spherical shell cap with and without a cutout [J]. Computers and Structures, 2002, 80(23): 1749-1756.

[7] Hosseini-Hashemi S, Fadaee M. On the free vibration of moderately thick spherical shell panela new exact closed-form procedure[J]. Journal of Sound and Vibration,2011,330(17): 4352-4367.

[8] Su Z, Jin G, Ye T. Free vibration analysis of moderately thick functionally graded open shells with general boundary conditions [J]. Composite Structures,2014,117:169-186.

[9] Kang J H, Leissa A W. Three-dimensional vibrations of thick spherical shell segments with variable thickness[J]. International Journal of Solids and Structures,2000,37: 4811-4823.

[10] Kang J H, Leissa A W. Three-dimensional vibration analysis of solids and hollow hemispheres having varying thicknesses with and without axial conical holes[J]. Journal of Vibration and Control, 2004, 10: 199-214.

[11] Ascher U, Christiansen J, Russell R D. Collocation software for boundary value ODEs[J]. ACM Transactions on Mathematical Software, 1981, 7(2): 209-222.

[12] Ascher U, Christiansen J, Russell R D. Algorithm 569, COLSYS: collocation software for boundary value ODEs [D2] [J]. ACM Transactions on Mathematical Software,1981,7(2):223-229.

[13] Williams F W, Wittrick W H. An automatic computational procedure for calculating natural frequencies of skeletal structures[J]. International Journal of Mechanical Sciences, 1970, 12(9): 781-791.

[14] Wittrick W H, Williams F W. A general algorithm for computing natural frequencies of elastic structures[J]. Quarterly Journal of Mechanics and Applied Mathematics, 1971, 24(3): 263-284.

[15] Yuan S, Ye K, Xiao C, et al. Exact dynamic stiffness method for non-uniform Timoshenko beam vibrations and Berboulli-Euler column buckling[J]. Journal of Sound and Vibration, 2007, 303(3/4/5): 526-537.

[16] 叶康生,赵雪健. 动力刚度法求解平面曲梁面外自由振动问题[J]. 工程力学,2012,29：1-8.

YE Kang-sheng, ZHAO Xue-jian. Dynamic stiffness method for out-of-plane free vibration analysis of planar curved beams [J]. Engineering Mechanics, 2012, 29: 1-8.

[17] Su H, Banerjee J R, Cheung C W. Dynamic stiffness formulation and free vibration analysis of functionally graded beams [J]. Composite Structures, 2013, 106: 854-862.

[18] El-Kaabazi N, Kennedy D. Calculation of natural frequencies and vibration modes of variable thickness cylindrical shells using the Wittrick-Williams algorithm[J]. Computers and Structures, 2012, 104/105: 4-12.

[19] Gautham B P, Ganesan N. Free vibration analysis of thick spherical shells[J]. Computers and Structures,1992,45(2): 307-313.

[20] Shim H J, Kang J H. Free vibration of solid and hollow hemi-ellipsoids of revolution from a three-dimensional theory [J]. International Journal of Engineering Science,2004,42:1793-1815.

Free vibration analysis of moderately thick elliptical shells using the dynamic stiffness method

CHENXu-dong1，YEKang-sheng2

(1. School of Naval Architecture and Civil Engineering, Jiangsu University of Science and Technology, Zhangjiagang 215600,China；2. Key Laboratory of Civil Engineering Safety and Durability of China Education Ministry, Department of Civil Engineering, Tsinghua University, Beijing 100084, China)

Abstract:The application of exact dynamic stiffness method to the free vibration analysis of moderately thick elliptical shells was introduced. The free vibration of moderately thick elliptical shells was decomposed into a series of one-dimensional vibration problems corresponding to structural vibration modes with different circumferential wave numbers. For each one-dimensional vibration problem, the governing equation was written in Hamilton form, from which the dynamic stiffness expression of the one-dimensional problem was derived. The governing equations were solved by using the ordinary differential equations solver COLSYS and the dynamic stiffnesses of elements were obtained. By applying the Wittrick-Williams algorithm, the natural frequencies under the vibration mode with a specific circumferential wave number were found. Numerical examples of moderately thick spherical and elliptical shells with different boundary conditions were given, showing that the dynamic stiffness method is robust, reliable and accurate.

Keywords:elliptical shells; free vibration; dynamic stiffness method; Wittrick-Williams algorithm; Hamilton form

中图分类号:TU311.3

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.06.015

通信作者叶康生 男，博士，副教授，1972年生

收稿日期：2015-07-09修改稿收到日期：2015-10-14

基金项目：国家自然科学基金项目(51078198)；清华大学自主科研计划(2011THZ03);江苏省双创博士

第一作者 陈旭东 男，博士，讲师，1984年生