基于定向循环均值的滑动轴承失稳信号分析

柏　林， 陈　杨， 彭　畅

(1.重庆大学 机械传动国家重点实验室，重庆　400044;2.中车青岛四方机车车辆股份有限公司 国家工程研究中心，山东 青岛　266000)



基于定向循环均值的滑动轴承失稳信号分析

柏林1， 陈杨1， 彭畅2

(1.重庆大学 机械传动国家重点实验室，重庆400044;2.中车青岛四方机车车辆股份有限公司 国家工程研究中心，山东 青岛266000)

摘要：为综合描述滑动轴承转子系统在失稳状态下的振动状况，提出基于定向循环均值的信号分析方法。将用于单通道实信号分析的一阶循环统计量进行扩展并定义正交双通道融合复信号的定向循环均值，给出基于定向循环均值的轴心轨迹簇提取步骤。利用转子试验台模拟滑动轴承旋转机械的失稳故障获取数据，分析结果表明,该方法不仅能提取系统在一截面内的周期性振动特征，揭示转子在指定循环频率处的旋向，且基于定向循环均值的轴心轨迹簇与传统全息谱相吻合，从而验证该方法的有效性。

关键词：滑动轴承；油膜失稳；定向循环均值；轴心轨迹

受复杂工况下背景噪声的影响以及损伤部件的作用，机械设备的振动信号往往呈现出非线性、非平稳等特点。旋转机械由于其关键零部件(如转轴、齿轮、轴承等)具有对称特性，且其运动方式为旋转运动，运行中所产生的振动信号常常包含一些与自身结构密切相关的周期特性[1]，这种周期特性是其它非线性信号所不具备的。然而诸如时频分析、小波分析和非线性时间序列分析等传统的非平稳信号分析方法则在处理旋转机械振动信号时容易忽略信号中包含的周期特性。

为解决上述问题并准确提取非平稳振动信号中的周期性时变特性，循环平稳理论由于其独特优势近年来得到了广泛的关注与发展。李力等[2-3]将循环谱密度函数用于滚动轴承与齿轮故障信号的特征提取和解调分析，有效地消除了非同频成分的干扰。姜鸣[4]利用调幅信号的循环谱密度函数在强噪声条件下准确提取了滚动轴承故障特征频率。毕果等[5-7]基于平滑循环周期估计算法以及Hilbert变换进一步强化了切片分析技术，并结合循环维纳滤波器实现了故障信号的自适应滤波。周宇等[8]基于循环统计量提出了循环双谱的频移算法以及一、二次切片分析技术，实现了滚动轴承早期故障预示。Gardner等[9-10]以大量离散循环平稳信号为研究对象，基于矩阵与累计理论研究了循环平稳特性在特征提取、模式识别与系统分辨中的潜力。

以上介绍的循环平稳分析方法仅局限于处理单通道振动信号，而轴承-转子系统在垂直和水平两个方向上的振动信号被相互孤立考虑，以致很难掌握系统在某一截面内的完整振动情况。为融合正交双通道信号综合描述转子在一个测量截面上的运行状态，避免单通道信号分析方法中存在的缺陷，本文将传统的一阶循环统计量进行扩展并定义复信号定向循环均值，介绍基于双通道融合复信号定向循环均值的轴心轨迹提取方法，研究分析滑动轴承转子系统在一阶共振、油膜涡动和油膜振荡下实测振动信号的循环平稳特性。通过将基于定向循环均值的轴心轨迹提取结果与经典的二维全息谱进行对比，总结归纳定向循环均值在描述滑动轴承转子系统失稳状态时的有效性及优越性。

1复信号分解

设x(t)和y(t)分别表示两个单通道的正弦实信号，定义复信号为

r(t)=x(t)+jy(t)

(1)

式中:r(t)为一作椭圆运动的向量。由于椭圆运动可以表示为两个旋向相反的圆运动向量之和(见图1)[11]，可利用欧拉公式将转频为ω的向量r(t)表示为极坐标形式，即

r(t)=rf(t)+rb(t)=rfejωt+rbe-jωt

(2)

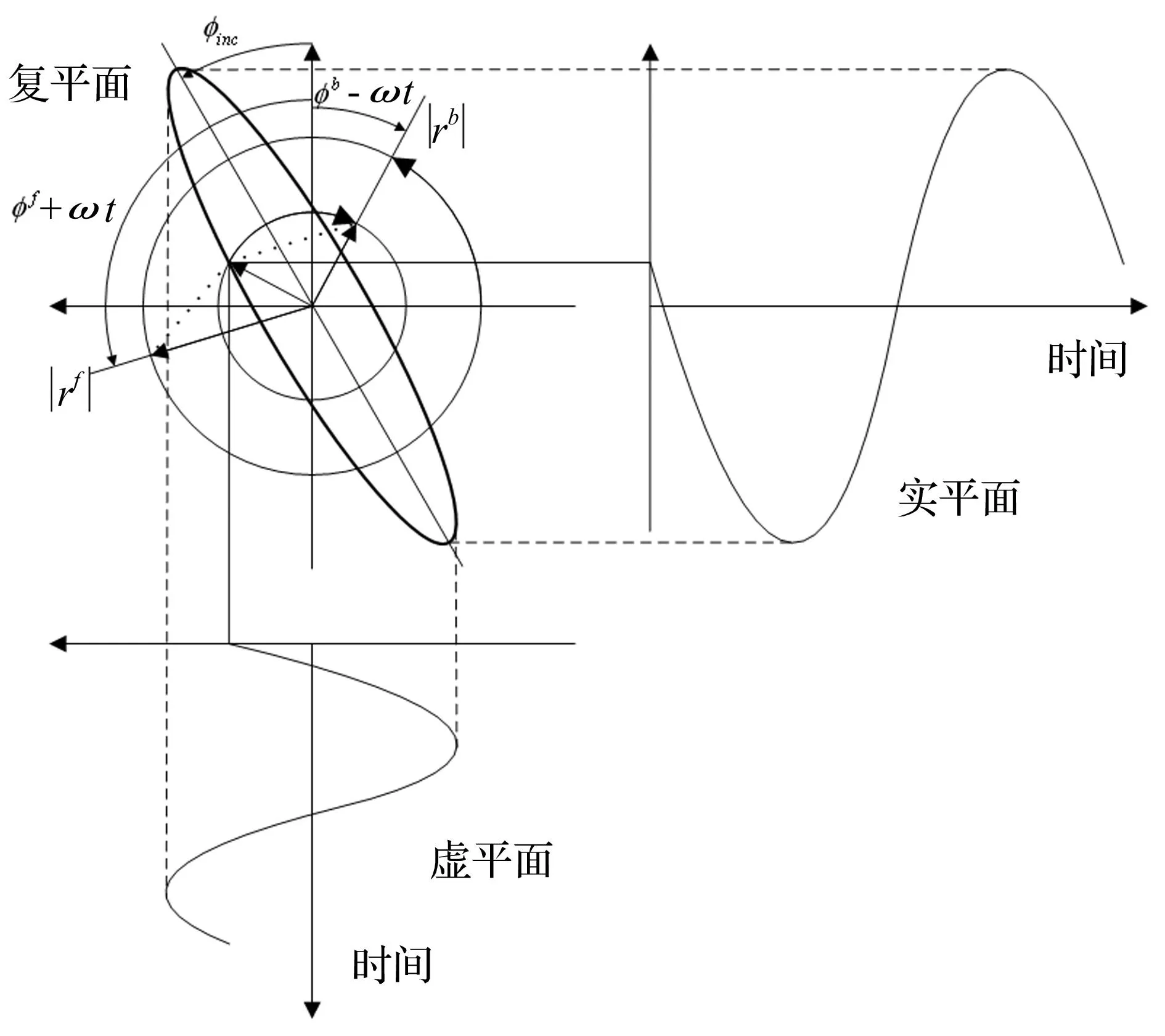
图1　复信号表示为两个反向旋转圆向量之和Fig.1 Representation of a complex-valued signal as the sum of two contra-rotating vectors

实信号x(t)和y(t)可据傅里叶系数展开，即

(3)

式中：xc、xs、yc和ys为对应的傅里叶系数。

正反进动的圆向量可以表示为

(4)

2定向循环均值及轴心轨迹提取方法

2.1定向循环均值

循环平稳分析中对随机信号x(t)进行非线性变换的最小阶数称为循环平稳信号阶数，其中所提取的正弦波的周期定义为循环周期Tω，其频率称为循环频率ω，所有的循环频率集合称为循环频率域。

定义循环频率ω处的循环均值为

商鞅变法是我国历史上较为彻底、较为成功的改革，实现其最初提出的富国强兵的目标，为此后秦国灭亡六国、统一中国奠定了基础。如上所述，商鞅变法中大部分内容涉及财政改革，从财政角度分析研究商鞅变法，汲取其变法的经验教训，对当前深化财政改革具有现实意义。

Eω{x(t)}=E0{x(t)e-j2πωt}=

(5)

式中：E0=limT→∞[∫x(t)dt]/T为x(t)在ω=0处的均值，T为时间长度。

将全部循环频率上的均值求和可以得到循环平稳信号在循环频率域上的一阶循环平稳统计量，即循环均值(Cyclic Mean, CM)[12]。

(6)

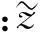
将传统的单通道实信号循环平稳均值方法进行扩充用于分析复信号r(t)=x(t)+jy(t)，通过融合两个正交通道振动信号的幅值、频率以及相位信息，能够更完整的描述转子在某一横截面内的振动状态。

根据式(2)，复信号r(t)可以分解为正进动解析信号rf(t)和反进动解析信号rb(t)，则可以根据式(6)定义正进动定向循环均值(Forward Directional Cyclic Mean)DCMf(ω)和反进动定向循环均值(Backward Directional Cyclic Mean)DCMb(ω)

(7)

在全循环频率轴上整合正反进动定向循环均值，得到复信号r(t)的定向循环均值(Directional Cyclic Mean，DCM)以表征转子平均周期性振动行为。

DCM(ω)=

(8)

2.2基于定向循环均值的轴承轨迹提取

R(t)=R+ωej(ωt+αω)+R-ωe-j(ωt+βω)

(9)

式中：R+ω、R-ω分别为正反进动圆的半径长度。如果R+ω>R-ω则转子在频率ω处的轴心轨迹椭圆旋向为正进动，反之旋向则为反进动。一般情况下旋转机械的旋向为正进动居多，若出现反进动，则故障往往不是失衡而是其它故障，例如动静部件碰磨所引起的故障[13]。

基于DCM的轴心轨迹提取方法见图2。首先用相互垂直的X、Y两个通道的信号构成复信号r(t)=x(t)+jy(t)，然后计算出r(t)的定向循环均值，进而得到转子在频率ω处的正反进动圆的运动半径和初始相位，接着如图1所示合成转子在ω处的轴心轨迹，在一系列不同的频率ωi(i=1,2,3...)处合成转子的轴心轨迹从而得到轴心轨迹簇。

图2　基于DCM的轴心轨迹簇提取方法示意图Fig.2 Interpretation of the axis orbit based on DCM

与基于DCM的轴心轨迹提取方法进行对比，在此简要介绍全息谱技术[13]，其构成原理见图3。全息谱以傅里叶变换为基础，利用机组振动信号频率的谱线加以集成而得到在不同频率上的轴心轨迹簇。

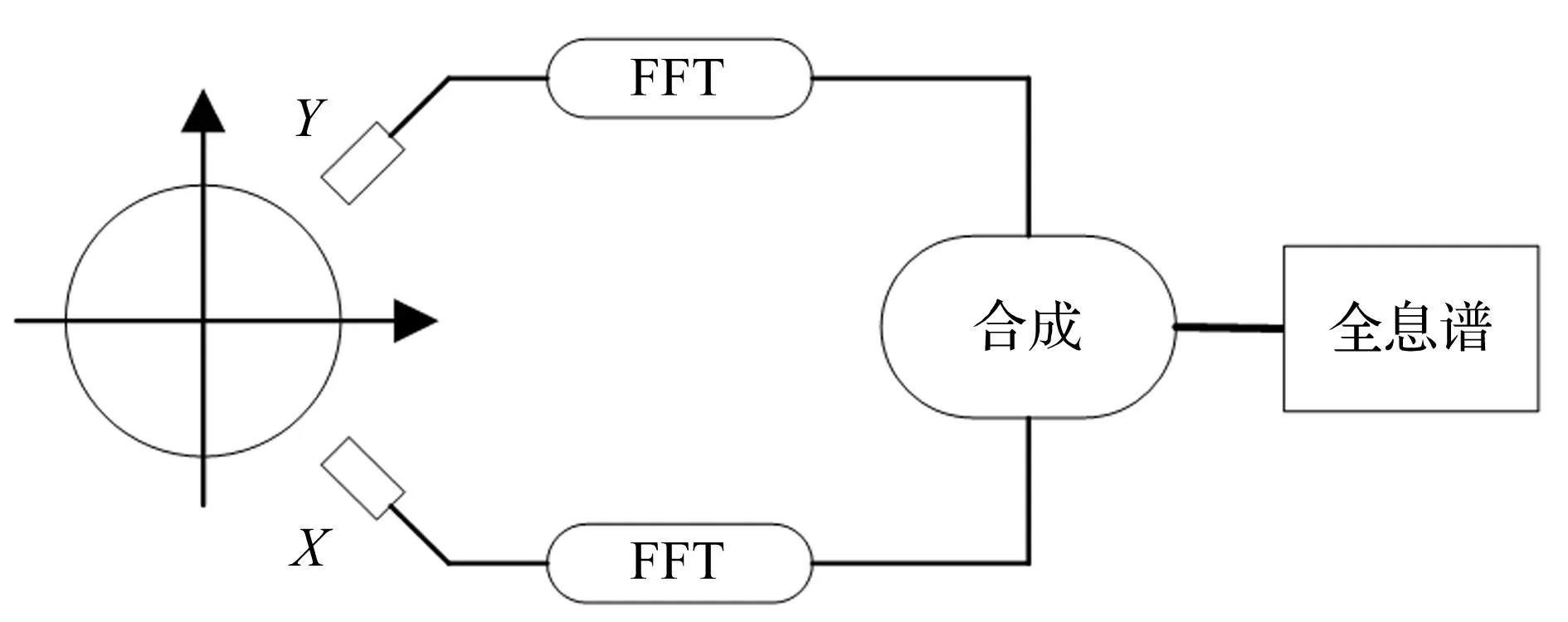
图3　基于FFT的二维全息谱原理Fig.3 Interpretation of the 2D holospectrum based on FFT

3油膜涡动与油膜振荡信号分析

3.1定向循环均值分析

为了验证所提出的定向循环均值及基于DCM的轴心轨迹提取方法在分析滑动轴承转子系统失稳状态时的有效性，采用INV1612型柔性转子实验系统进行实测试验，整个试验装置见图4。两个型号为JX70-015-E-M10的电涡流传感器相互垂直安装在转轴中间位置的支座上，分别拾取转轴在X、Y方向上的位移振动信号。型号为WO-DNMW2的光电式转速传感器实现了将转轴的转速转换成脉冲电压信号的功能。采用NI 9234型采集卡对振动及转速信号进行多通道同步采集。

图4　滑动轴承柔性转子实验台Fig.4 Test bench and its main components

滑动轴承转子系统常见的失稳形式有系统共振、油膜涡动、油膜振荡等[14]，因此本文对系统在一阶共振、油膜涡动、油膜振荡三种状态下的转子振动位移信号进行分析。图5、图6分别为系统在上述三种状态下X、Y通道的时域信号，其中信号长度N=4 096，采样频率fs=2 048 Hz。首先用循环均值方法对单通道时域信号进行分析，然后用本文提出的定向循环均值法对有X、Y通道信号构成的复信号r(t)=x(t)+jy(t)进行分析。在下面的叙述中X1、X2、X3分别表示系统在一阶共振、油膜涡动和油膜振荡状态下的转频，即电机的转动频率,其中X1≈50 Hz，X2≈91.5 Hz、X3≈103.3 Hz，fowl、fowp分别表示油膜涡动与油膜振荡频率。

图5　滑动轴承转子系统失稳X通道时域振动信号Fig.5 X-channel Vibration signal of journal bearing supported system under unstable state

图6　滑动轴承转子系统失稳Y通道时域振动信号Fig.6 Y-channel vibration signal of journal bearing supported system under unstable state

图7、图8分别为转子X、Y通道一阶共振振动信号的循环均值，可以看到系统的一阶共振频率X1约为50 Hz。系统在油膜涡动状态下转子在润滑油团的作用下其中心线偏离轴瓦中心线，油团转速约为转子转频的1/2，所以油膜涡动又称为半速涡动，油膜涡动频率通常为转频的(0.42～0.49)倍数[16]。由图9、图10可知,明显的油膜涡动特征频率fowl=0.475X2(43.5 Hz)。油膜振荡是油膜涡动的进一步发展，随着转速增加，振荡频率保持不变，并且振动更加剧烈，因此危害性更大。从图11、图12也可以发现明显的油膜振荡特征频率fowp=0.473X3(48.9 Hz)。然而，单通道信号的循环均值只能分别得到系统在单个方向上的振动幅值信息，忽略了正交两个方向振动状态之间存在的内在联系，不能揭示系统在一个面内的运行状况。

图7　转子一阶共振X通道振动信号循环均值Fig.7 The cyclic mean of X-channel vibration signal of rotor under resonance

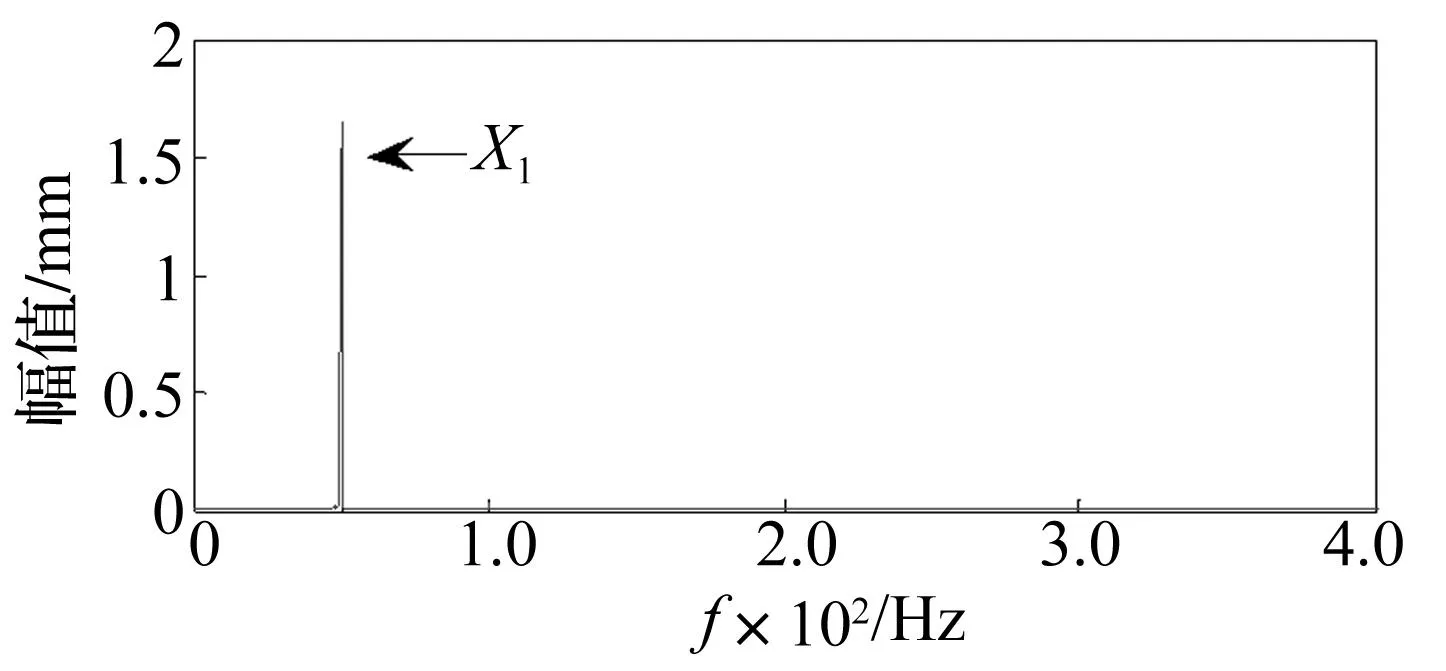
图8　转子一阶共振Y通道振动信号循环均值Fig.8 The cyclic mean of Y-channel vibration signal of rotor under resonance

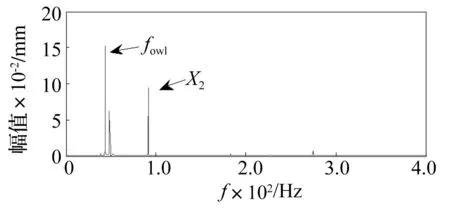
图9　转子在油膜涡动状态下X通道振动信号的循环均值Fig.9 The cyclic mean of X-channel vibration signal of rotor during oil whirl

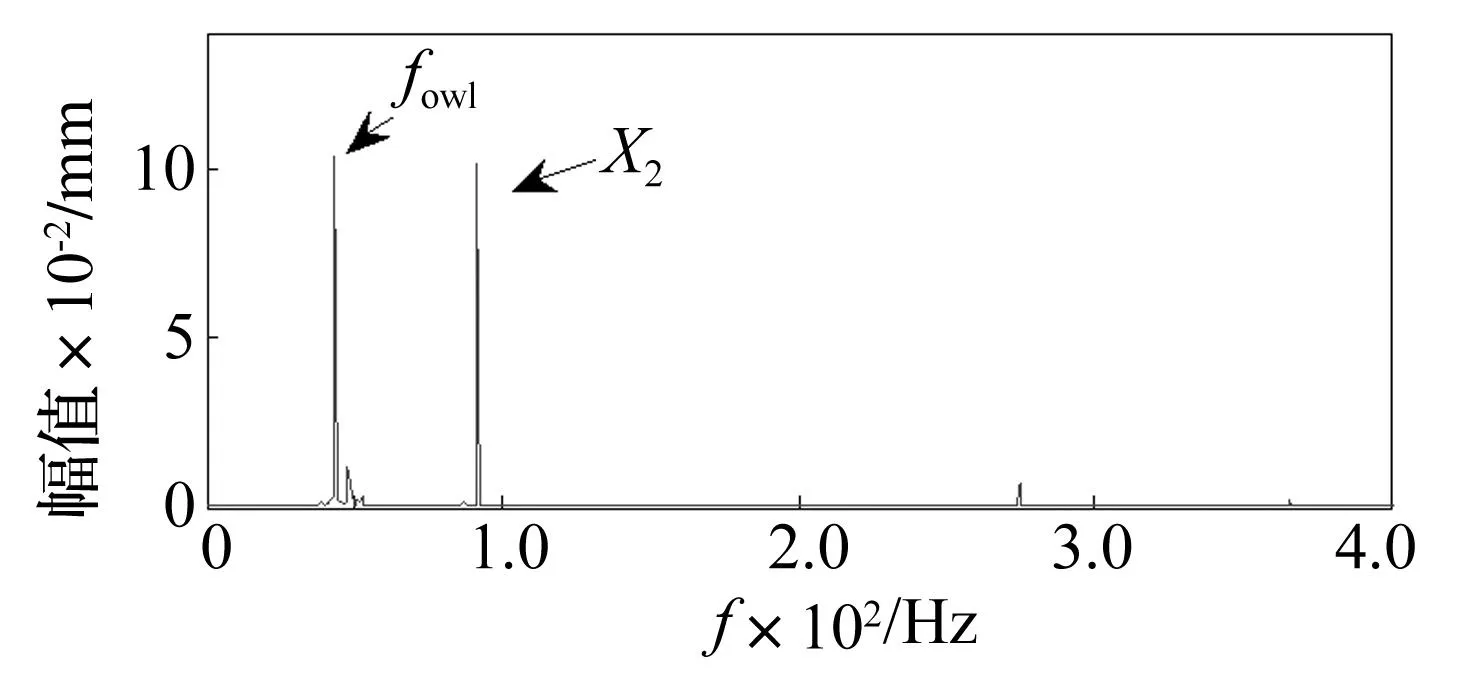
图10　转子在油膜涡动状态下的Y通道振动信号的循环均值Fig.10 The cyclic mean of Y-channel vibration signal of rotor during oil whirl

图11　转子在振荡状态下的X通道振动信号的循环均值Fig.11 The cyclic mean of X-channel vibration signal of rotor during oil whip

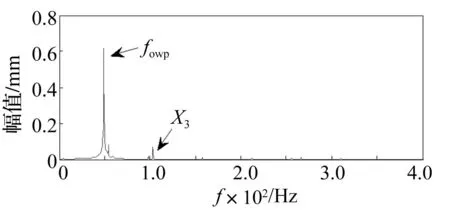
图12　转子在振荡状态下的Y通道振动信号的循环均值Fig.12 The cyclic mean of Y-channel vibration signal of rotor during oil whip

本文利用转子一个横截面内相互垂直的两个通道信号构造复信号r(t)=x(t)+jy(t)，并分别计算系统一阶共振、油膜涡动和油膜振荡下复信号r(t)的定向循环均值,见图13～图15。定向循环均值图中横轴表示圆运动的旋转频率，正频率表示圆运动为正进动，负频率表示圆运动为反进动，纵轴表示进动圆相对半径长度即振动幅值。图13中存在+X1、-X1两个特征频率，这是由于系统一阶共振引起的，正转频处的幅值R+X1大于负转频处的幅值R-X1，R+X1>R-X1，所以系统在共振频率X1处旋向为正进动，由图14可知,油膜涡动特征频率fowl=±0.475X2(43.5 Hz)以及转频±X2(91.5 Hz)。此外正转频+X2处的幅值明显远大于负转频-X2处的幅值，R+X2>R-X2,表明在转频X2处系统存在不平衡且旋向为正进动。另外正涡动频率处的幅值大于负涡动频率处的幅值，R+fowl>R-fowl，故转子在油膜涡动频率fowl处的旋向为正。由图15可知，系统在油膜振荡状态下的定向循环均值图同样可以发现油膜振荡特征频率成分fowp=±0.473X3(48.5 Hz)，并且转频±X3(103.3 Hz)处的幅值远小于转子在油膜振荡fowp处的幅值，表明油膜振荡在转子振动中起主导作用。此外正振荡频率处的幅值大于负振荡频率处的幅值R+fowp>R-fowp，故转子在振荡频率处的旋向为正。

图13　转子一阶共振状态下复信号定向循环均值Fig.13 The DCM of the vibration of the rotor under resonance

图14　转子油膜涡动状态下复信号定向循环均值Fig.14 The DCM of the vibration of rotor during oil whirl

图15　转子油膜振荡状态下复信号定向循环均值Fig.15 The DCM of the vibration of the rotor during oil whip

3.2基于DCM的轴心轨迹提取

为了进一步描述滑动轴承转子系统在油膜失稳状态下的振动状态，本文依据“2.2”介绍的基于DCM的轴心轨迹提取方法，分别提取了系统在转频X、倍频2X、3X、4X以及0～X频率区间内主要频率处的轴心轨迹簇,见图16～图18。图中直观地呈现出了系统在各个频率处的轴心轨迹以及旋向，由图16可知转频X1处存在一个做正进动的轴心轨迹椭圆，由图17可知,转频X2以及油膜涡动频率fowl=0.475X2存在两个明显的轴心轨迹椭圆，此外由于油膜振荡状态下油膜振荡起主导作用，由图18可知,相对于其余频率处的轴心轨迹，油膜振荡频率fowp=0.47X3处的椭圆轨迹十分明显。

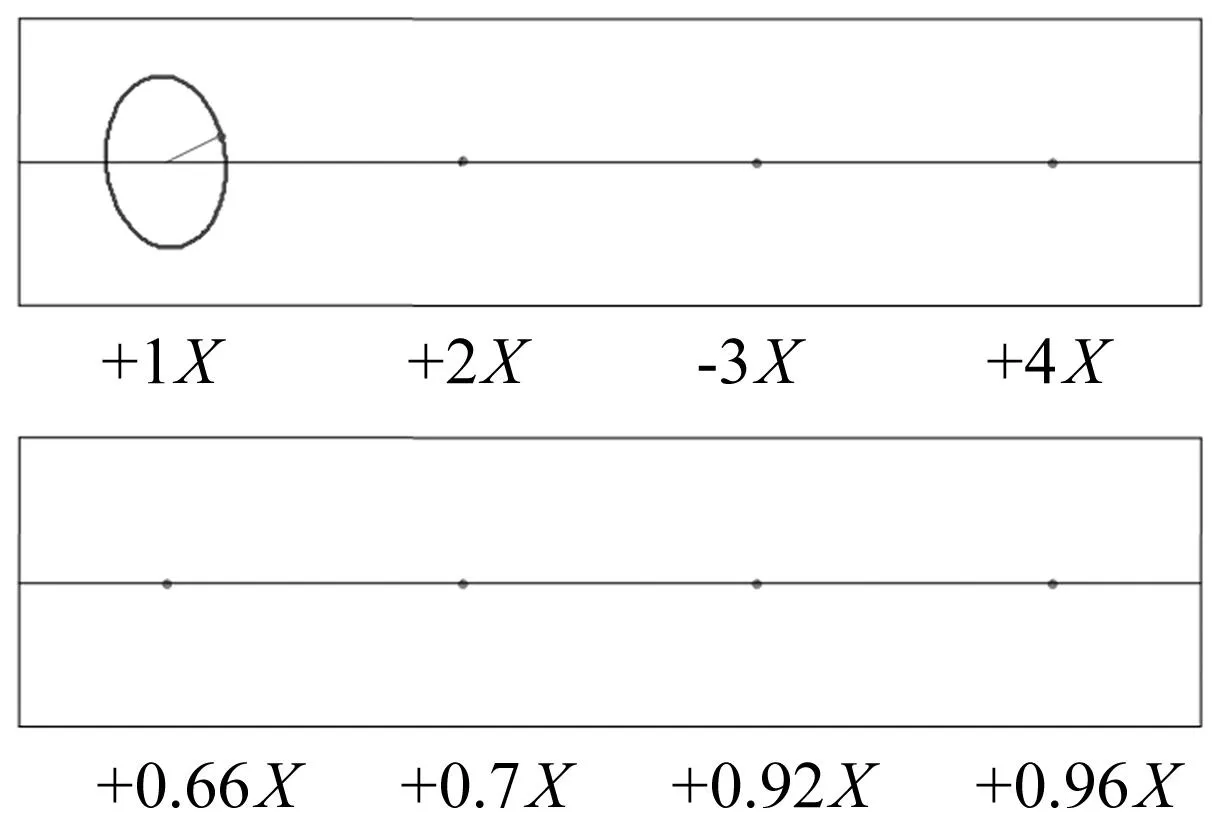
图16　基于定向循环均值的转子一阶共振轴心轨迹簇Fig.16 The DCM based axis orbit of rotor under resonance

图17　基于定向循环均值的转子油膜涡动轴心轨迹簇Fig.17 The DCM based axis orbit of rotor during oil whirl

图18　基于定向循环均值的油膜振荡轴心轨迹簇Fig.18 The DCM based axis orbit of rotor during oil whip

图19～图21分别给出了系统相应的全息谱。图16、图17分别与图19、图20对比可知,在一阶共振和油膜涡动状态下通过两种方法得到的轴心轨迹的大小、形状、相位以及旋向均保持了高度一致，由此也可以推循环均值与传统的FFT变换存在某种内在联系；而图18与图21在油膜振荡频率fowp=0.47X3处轴心轨迹初相位存在较小差异。与一阶共振和油膜涡动相比，油膜振荡的非平稳特性更加突出，而FFT的分析对象是平稳信号，从而导致了基于FFT的全息谱与基于DCM的轴系轨迹出现了上述差异。

图19　转子一阶共振的二维全息谱Fig.19 The 2D holospectrum of rotor under resonance

图20　转子油膜涡动的二维全息谱Fig.20 The 2D holospectrum of rotor during oil

图21　转子油膜振荡的二维全息谱Fig.21 The 2D holospectrum of rotor during oil whip

4结论

为了综合描述滑动轴承转子系统在失稳现象下的振动状态，本文提出了分析双通道融合复信号的定向循环均值方法，经试验验证结论如下：

(1) 相对于传统单通道信号的循环平稳分析，DCM方法不仅能够提取在一阶共振、油膜涡动及油膜振荡状态下系统某一截面内循环平稳振动信号的中周期性特征，而且能够揭示转子在指定循环频率处的旋向，从而准确地描述滑动轴承转子系统运行状态。

(2) 基于定向循环均值所提取的转子轴心轨迹簇能够更加直观地描述系统的振动状态，对于一阶共振和油膜涡动，其与全息谱所得到的转子轴心轨迹形状、大小、相位及旋向等信息均保持一致；对于非平稳特性更加突出的油膜振荡信号，通过定向循环均值提取的轴心轨迹更加准确，从而证明了该方法的有效性。

参 考 文 献

[1] 姜鸣, 陈进, 秦恺, 等. 一阶循环矩分析在旋转机械振动信号分析中的应用 [J]. 振动工程学报, 2001,14(4): 424-428.

JIANG Ming, CHEN Jin, QIN Kai, et al.Study on vibration signal for rotating machinery based on first-order cyclic moment analysis[J]. Journal of Vibration Engineering, 2001, 14(4): 424-428.

[2] 李力, 屈梁生. 循环统计量方法在滚动轴承故障诊断中的应用 [J]. 振动、测试与诊断, 2003, 23: 116-119.

LI Li, QU Liang-sheng. Application of cyclic statistics to fault diagnosis of rolling bearings[J]. Journal of Vibration, Measurement & Diagnosis, 2003, 23: 116-119.

[3] 李力, 屈梁生. 循环域解调方法在滚动轴承故障诊断中的应用 [J]. 轴承, 2003, 10: 33-36.

LI Li, QU Liang-sheng. Application of cyclic domain demodulation in fault diagnosis of rolling bearing[J]. Bearing, 2003, 10: 33-36.

[4] 姜鸣, 陈进, 秦恺. 时变调幅信号的循环平稳特征讨论和应用 [J]. 上海交通大学学报, 2001, 35: 1798-1801.

JIANG Ming, CHEN Jin, QIN Kai. Performance for time-varying amplitude modulation signal using cyclostationary approach[J]. Journal of Shanghai Jiaotong University, 2001, 35: 1798-1801.

[5] 毕果. 基于循环平稳的滚动轴承及齿轮微弱故障特征提取应用研究 [D]. 上海: 上海交通大学, 2007.

[6] Bi Guo, Chen Jin, He Jun,et al. Application of degree of cyclostationarity in rolling element bearing diagnosis [J]. Key Engineering Materials, 2005, (293/294): 347-354.

[7] Bi Guo, Chen Jin, Zhou Fu-chang, et al. Application of slice spectral correlation density to gear defect detection [J].Proceedings of the Institution of Mechanical Engineers,Part C: Journal of Mechanical Engineering Science, 2006, 220: 1385-1392.

[8] 周宇. 基于循环平稳信号二维平面表示的滚动轴承早期故障诊断方法研究 [D]. 上海: 上海交通大学, 2012.

[9] Gardner W A. Stationarizable random processes [J]. IEEE Transactions on Information Theory, 1978, 24: 8-22.

[10] Gardner W A. Spectral correlation of modulated signals: part I—analog modulation[J].IEEE Transactions on Communication, 1987, 35: 584-594.

[11] Han Y S, Lee C W. Directional wigner distribution for order analysis in rotating/reciprocating machines[J]. Mechanical Systems and Signal Processing, 1999, 13(5): 723-737.

[12] Chang Peng, Lin Bo. Vibration signal analysis of journal bearing supported rotor system by cyclostationarity[J].Shock and Vibration, 2014, 2014:952958.

[13] 屈梁生. 机械故障的全息诊断原理[M]. 北京：科学出版社，2007.

[14] 马辉，李辉，牛和强，等.滑动轴承-转子系统油膜失稳参数影响分析[J].振动与冲击,2013,32(23):100-104.

MA Hui,LI Hui,NIU He-qiang,et al.Parametric influence analysis of oil-film instability in a sliding bearing-rotor system[J].Journal of Vibration and Shock,2013,32(23):100-104.

Directional cyclic mean-based method for instable journal bearing signal analysis

BOLin1,CHENYang1,PENGChang2

(1. The State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, China;2. Engineering Research Center, CRRC Qingdao Sifang CO., LTD., Qingdao 266000, China)

Abstract:For comprehensive description of unstable operation of a journal bearing supported rotor system, a new instable signal analysis method called directional cyclic mean(DCM) was presented. With this method, the traditional 1st order cyclic statistic dealing with a single channel's real signal analysis was extended and the 1st order directional cyclic mean statistic for fused complex signals of orthogonal double channels was defined. And the procedure of extracting axis orbits based on DCM was given. To verify this method, a rotor test platform was used to imitate unstable fault of rotor-bearing systems. The analysis of experimental data showed that the periodic vibration characteristics and rotating direction of a cross-section of a rotor-bearing system can be found; furthermore, axis orbits based on DCM agree well with those of the traditional holospectrum; the effectiveness of DCM is verified.

Key words:journal bearing; oil-film instability; directional cyclic mean; axis orbit

中图分类号:TH17; TP206

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.06.006

通信作者陈杨 男，硕士生，1988年生

收稿日期：2014-07-16修改稿收到日期：2014-09-12

第一作者 柏林 男，博士，教授，博士生导师，1972年生