基于时间稳定性和降维因子分析的土壤水分监测优化①
刘玉娇,朱 青,吕立刚,廖凯华,徐 飞
(1 中国科学院南京地理与湖泊研究所,流域地理学重点实验室,南京 210008;2 中国科学院大学,北京 100049;3 南京大学地理与海洋科学学院,南京 210046)
基于时间稳定性和降维因子分析的土壤水分监测优化①
刘玉娇1,2,朱 青1*,吕立刚3,廖凯华1,徐 飞1
(1 中国科学院南京地理与湖泊研究所,流域地理学重点实验室,南京 210008;2 中国科学院大学,北京 100049;3 南京大学地理与海洋科学学院,南京 210046)
摘 要:以南京市高淳区青山茶场中相邻的茶园和竹林坡地为研究区,对研究区土壤水分进行长期定点监测。基于土壤水分时间稳定性,结合因子分析选取典型样点组合,采用多元线性回归模型构建各监测点土壤水与典型样点间的数量关系。通过典型样点预测各监测点土壤水分,并检验预测结果,以期通过少数样点的监测来反映研究区的整体概况,优化研究区土壤水分监测。结果表明:在茶园仅监测7个点时,验证期RMSE小于1.5 cm3/cm3;竹林仅监测5个样点时,验证期RMSE小于1.7 cm3/cm3,模型能很好地预测研究区各样点土壤水分,为优化土壤水监测、减少野外工作量提供了理论依据。不同土地利用方式、不同深度处土壤水分分布特征存在显著差异;竹林土壤水分具有较强的时间稳定性,土壤水分的空间自相关性较茶园强;30 cm深处比10 cm深处土壤水分具有更稳定的空间分布结构。
关键词:土壤水分;空间预测;时间稳定性;茶园;竹林
土壤水是生态系统中各圈层进行转化的重要纽带,土壤水分的运动是土壤物质迁移的主要驱动力之一[1-3]。污染物也可随土壤水的运动而扩散[4-6]。研究土壤水的分布和运动规律,对环境治理工程具有重要的指导意义[7]。而土壤是不均一变化的连续体[8],具有明显的时空差异[9-11],且这种空间变异是普遍存在的[12]。因此,精确监测和模拟土壤水分的时空变化难度较大。
土壤水是空间随机变量,可利用数理统计来研究土壤水分的空间分布规律[13],且这种规律是建立在时间稳定性基础上的。土壤水分的“时间稳定性”概念首先是由Vachaud等[14]于1985年首次提出,即空间采样点与土壤属性统计参数之间关系的时间不变性。当研究区是一个相对稳定的环境时,时间稳定性原理即成立,即不同时期测量的土壤水含量在空间上的分布具有极强的相似性[15]。基于此,以往许多研究尝试通过若干少数样点的土壤水分监测值来反映整个区域的土壤平均水分状况[16-18]。此外,由于土壤水分在空间上的相关性,未知点土壤水分可通过周围监测点进行估算,这为减少野外工作量,优化研究区土壤水分的监测提供了理论依据。
然而,由于地形地貌、土地利用和土壤性质的时空分异,同一研究区可以划分为不同的水文响应单元[19]。不同水文响应单元土壤水分稳定性特征不同[20-22],因此不能随意选择样点来代表研究区域的土壤水分状况。降维因子分析是在变量相关系数矩阵的基础上,把多个具有较强相关性的变量简化成少数几个综合变量,来研究总体信息的多元统计方法,且这少数的几个变量间不相关。因子分析为典型样点的选择提供了科学合理的方案。
本研究以南京市高淳区青山茶场作为研究区,在时间稳定性结合降维因子分析方法的基础上,选取典型样点,构建其与各监测点的数量关系,精确模拟各监测点的土壤水分,以期以较少监测点来反映研究区土壤水分的分布状况,减轻野外监测工作量,优化土壤水分监测。
1 材料与方法
1.1 研究区概况
研究区位于南京市高淳区青山茶场(E119°03′22″,N31°22′24″),该区属亚热带季风过渡气候,气候温和,四季分明,常年平均气温 16.4 ℃,年均降水量 1 194.5 mm,近 60% 的降雨集中在 6 至 9月,年日照数 2 128.1 h,农作物生长光热能量充足;海拔 15~35 m,系低丘倾斜平原。研究区平均坡度约为 12%,土地利用方式为茶园和毛竹林,土壤类型为薄层粗骨土。薄层粗骨土土层浅,厚度小于 1 m,砾石含量大于 30%,质地为轻壤土,土质松散。
根据坡面地形情况和土地利用类型,以8 m为取样间隔共设置77个土壤样点(图1),其中茶园39 个(编号1~40,30号空缺),毛竹林地38个(编号41~79,69 号空缺)。剖面土壤水分传感器(TRIME-PICOIPH)是基于TDR时域反射仪技术,通过测量土壤介电常数转换得到土壤水含量的测量仪器。采用剖面土壤水分传感器定期监测点10 cm、30 cm深处土壤水分,平均每月一次,基本覆盖干湿季,降雨较多的雨季进行加密观测,如5月10日、13日、15日均进行了监测,其中13、21、44、65号监测点未测得30 cm深处土壤水分。2012年12月至2013年12月,共测得14次土壤水分。将2013年3月至10月共10次监测数据用于构建样点土壤水间的回归模型,用2012年12月、2013年1月、11月、12月4次监测数据检验模拟结果,由于2012年12月竹林监测数据缺失,用2014年1月监测数据代替。
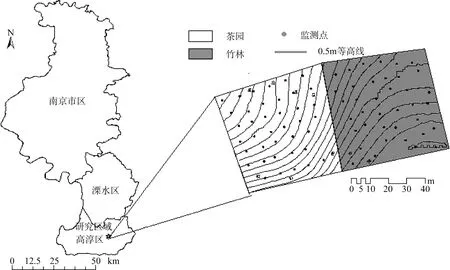
图 1 研究区域地理位置及监测点布置Fig.1 Location of study area and sampling sites in tea garden and bamboo forest
1.2 研究方法
土壤水分的时间稳定性公式如下:
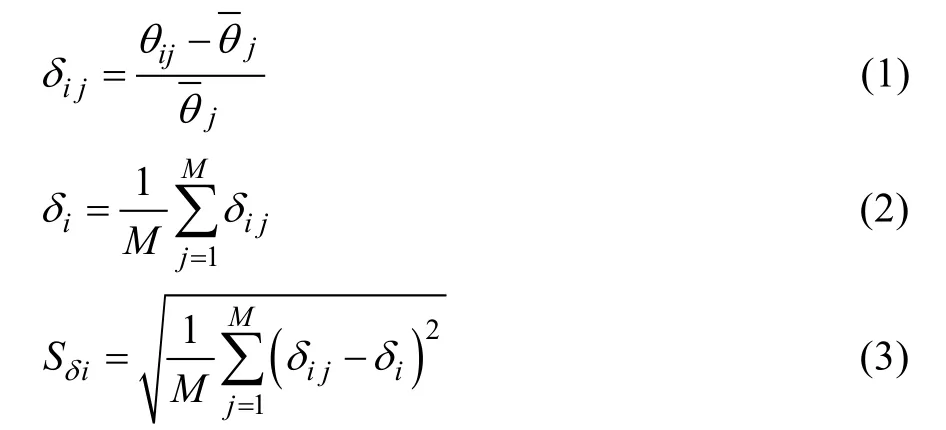
式中:θij为第j天第i个监测样点的实测土壤水分;为第j天所有监测样点实测土壤水分的平均值;δij为第j天第i个土壤水分监测样点的土壤水分相对偏差;δi为第i个监测样点所有监测时期的平均土壤水分相对偏差;M为监测次数(10次);Sδi为第i个监测样点所有监测时期土壤水分相对偏差的标准差。当δi为0时,该样点代表了研究区的平均湿润程度;当δi为正值时,该样点的湿润程度高于研究区的平均湿润程度;当δi为负值时则相反。Sδi越大,该样点土壤水分时间上越不稳定。
在时间稳定性的基础上,利用统计学分析各监测点土壤水分特征。在SPSS19.0中采用降维因子分析法,分别对茶园和竹林监测点3—10月土壤水分监测数据进行分析,使用主成分相关性分析法,得到因子分析旋转空间中的成分图。相关性较强的样点在图中集聚,结合由时间稳定性特征选取的典型样点,选取合适的监测点,使选取的典型样点尽量能表达研究区所有样点。最后,采用逐步多元线性回归(P<0.1),以典型样点土壤水分为自变量,其余样点为因变量,构建研究区样点与典型样点土壤水分的关系模型。由典型样点监测值,通过关系模型计算研究区各样点土壤水分,并用实测值进行检验,预测精度通过均方根误差(RMSE)进行综合评定。
2 结果与分析
2.1 时间稳定性分析
对茶园、竹林各监测点2013年3月至10月的土壤水分监测数据进行时间稳定性特征分析。研究区各样点的平均土壤含水量的相对偏差分布如图2所示,各样点的标准差使用垂直误差线标注。茶园土壤平均含水量相对偏差主要分布在 -0.5~0.5(图2A),有15个点土壤含水量相对偏差的标准差Sδi<0.1,时间稳定性较好;20个点Sδi在0.1~0.2,时间稳定性一般;4个点Sδi>0.2,时间稳定性较差。竹林土壤平均含水量相对偏差分布在 -0.4~0.4(图2B),其中22个样点土壤含水量时间稳定性较好,13个样点土壤含水量时间稳定性一般,3个样点时间稳定性较差。
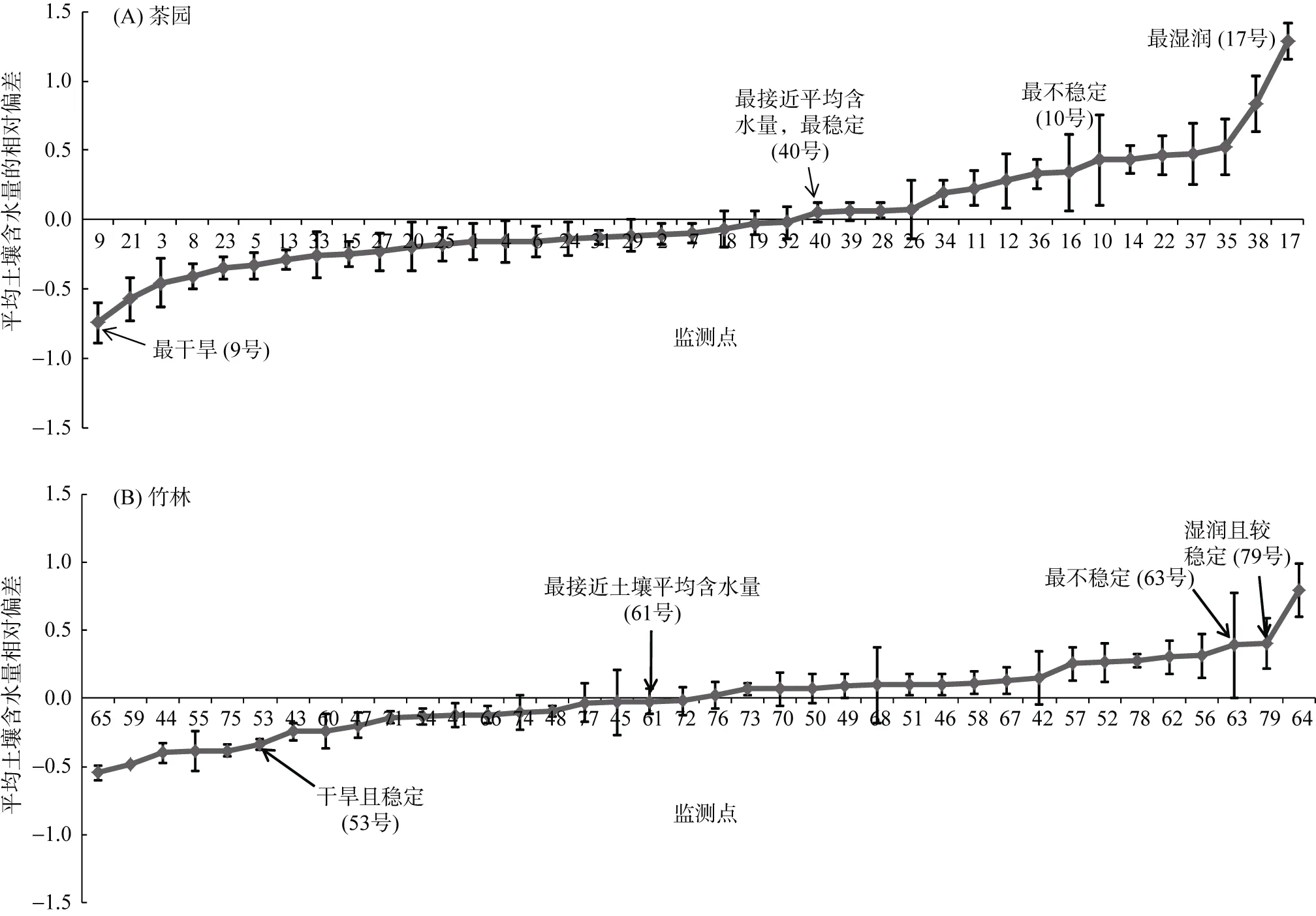
图2 茶园(A)、竹林(B)监测点平均土壤水分的相对偏差排序Fig.2 Rank of mean relative differences of soil moistures for(A)tea garden and(B)bamboo forest
在茶园监测点中,选取17号代表湿润的典型样点,40号代表接近土壤水分平均含量且时间稳定性最好的样点,9号代表干旱的样点;10号代表时间稳定性差的样点。同理,在竹林中,选取79号代表湿润度较高且稳定的典型样点,61号为最接近土壤平均湿度的样点,53号为干旱且稳定的样点,63号为时间稳定性差的样点。
当仅以时间稳定性选取的4个典型样点构建线性回归模型时,模型不能精确模拟研究区内所有样点土壤水分。在茶园10 cm深处,有 29个点模拟精度较好(R2>0.8),3个样点的模拟精度较差(R2<0.6);茶园30 cm深处,仅22个点模拟精度较好(表1)。在竹林10 cm深处,有35个点模拟精度较好,2个样点的模拟精度较差;30 cm深处,有 26个点模拟精度较好,2个样点的模拟精度较差(表2)。可见,当仅由时间稳定性选取的4个典型样点为自变量时,不足以精确模拟研究区监测点土壤水分含量。
2.2 降维因子分析
将3—10月共10次土壤水分进行降维因子分析,得到旋转空间中的成分图(图3)。成分图中样点的位置的远近表示其相关性的高低,综合考虑各样点间的相关性及已选取的典型样点,茶园可选出的样点有23号、12号和3号,竹林可选出的样点有55号、45号。
在已选定的典型样点的基础上,逐步添加由因子分析选择的样点作为自变量构建回归模型,观察模型决定系数R2。茶园逐步增加典型样点后,决定系数如表1所示。当以3、9、10、17、23、40、12号这7个典型样点作为自变量时,10 cm深处,有35个点模拟精度较好(R2>0.8),30 cm深度,有29个点模拟精度较好(表1)。10 cm深处模拟精度较好(R2>0.8)的样点数量占总监测量的89.7%,30 cm深处占78.4%,模型能较好地模拟研究区监测点土壤水分。
竹林在添加55号样点后(表2),10 cm深度,有36个点模拟精度较好(R2>0.8),仅1个样点的模拟精度较差(R2<0.6);30 cm深度,有32个点模拟精度较好。 10 cm深处模拟精度较好(R2>0.8)的样点占总监测数的94.73%,30 cm深处占88.89%(表2)。竹林仅监测5个样点时,模型精度已很好,无需再添加45号样点。
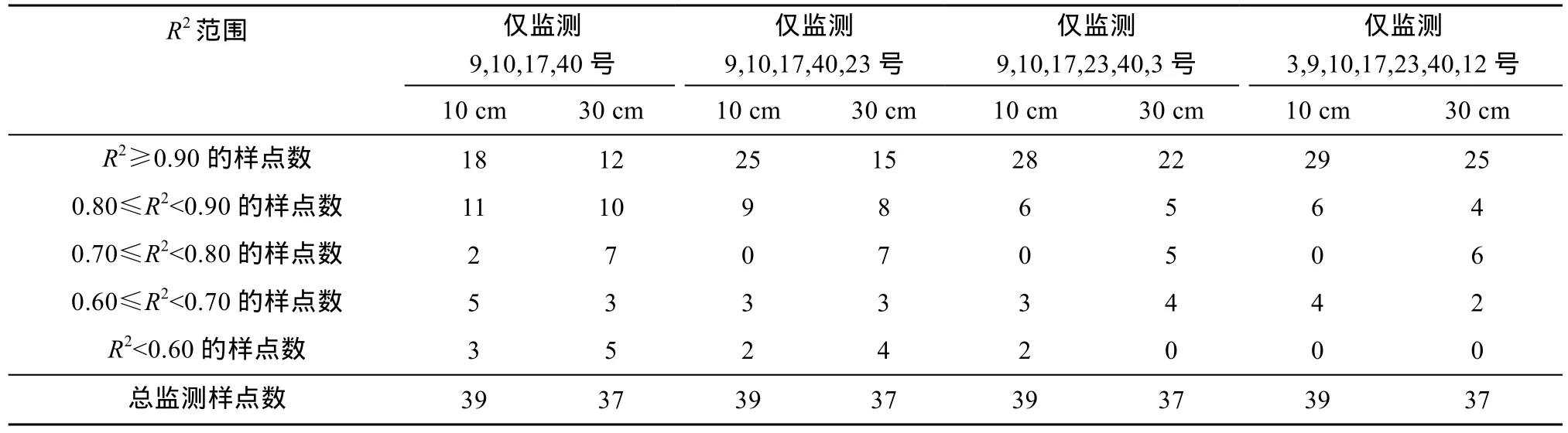
表1 茶园典型样点回归模型决定系数R2值分布情况Table 1 R2values of regression models for different representative sampling sites in tea garden
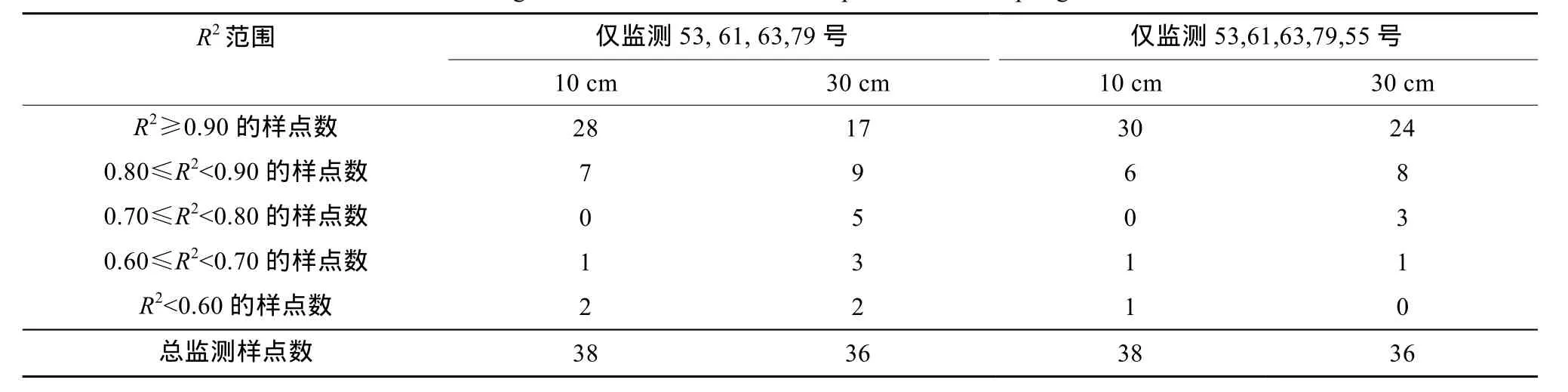
表2 竹林典型样点回归模型决定系数R2值分布情况Table 2 R2values of regression models for different representative sampling sites in bamboo forest
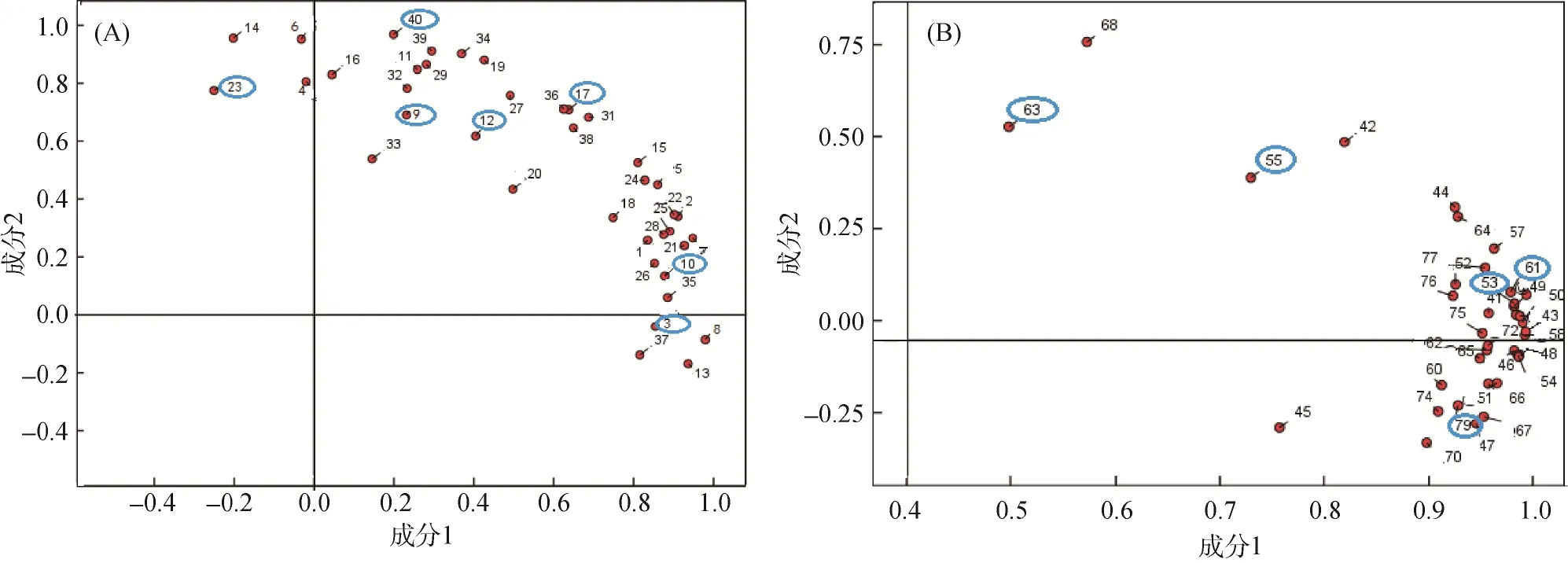
图3 茶园(A)、竹林(B)监测点在旋转空间中的成分图Fig.3 Component diagrams of sampling sites for tea garden(A)and bamboo forest(B)
2.3 检验分析
2.3.1 模型检验结果 茶园、竹林2013年3—10月各监测点模拟的效果总体较好(图4)。10 cm深处,除9月26日偏差最大为1.15 cm3/cm3外,其余模拟结果都较好;30 cm深处,RMSE均小于1 cm3/cm3。竹林整体的模拟效果也较好,但部分样点偏差较大(图4)。竹林10 cm深处模拟效果较差为5月13日,30 cm深处较差的是5月15日,其余各时期RMSE均小于1.5 cm3/cm3。茶园、竹林在降雨后监测的5月模拟效果均较差,原因可能是受到降雨的影响,土壤水在空间上分布结构短时间内发生变化[23],湿润期与干旱期土壤空间分布的变异性差异较大[24],造成部分样点土壤水分模拟偏差大,以致总体模拟效果差。
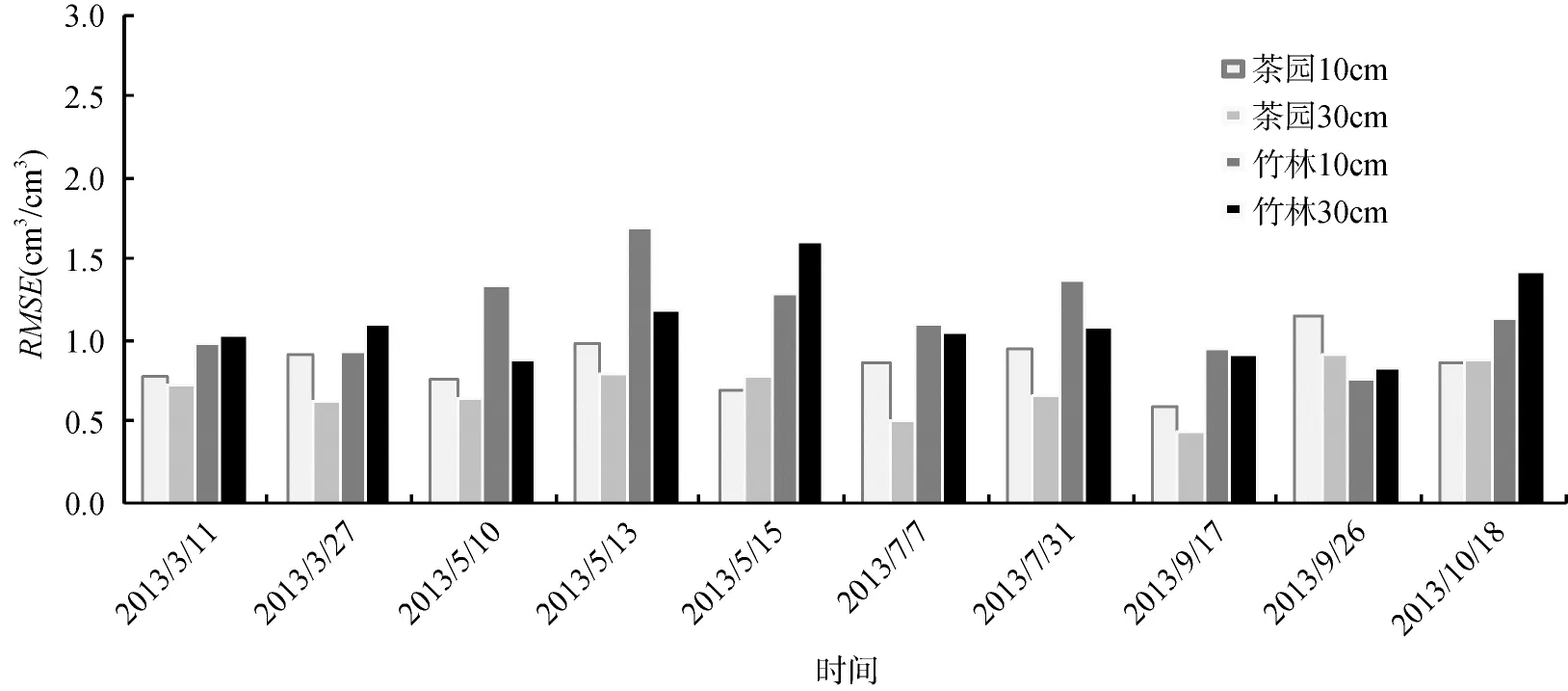
图4 训练期茶园、竹林模型检验的RMSEFig.4 RMSE Values of soil moistures for tea garden and bamboo forest during training period
茶园监测点验证期的模拟效果较好,各监测点预测值与实测值较为吻合。验证期监测点预测均值与实测均值较为接近,差值均小于0.5 cm3/cm3。10 cm深处,2013年1月9日的RMSE最小,为0.88 cm3/cm3,RMSE占实测平均值的7.98%。30 cm深处,2012年12月18日的RMSE最小,为1.11 cm3/cm3,RMSE占实测平均值的9.71%(表3),仅11月13日的预测平均值与实测平均值的差异较大,为1.24 cm3/cm3。
竹林监测点验证期实测值与预测值接近,模型能很好地反映研究区土壤水分的平均状况。10 cm深度2013年11月13日的RMSE最小,为1.34 cm3/cm3,RMSE占实测平均值的比例也较小,为10.29%;30 cm深处,除误差大的2013年1月外,各时期的预测均值与实测均值较为接近(表4),2013年11月13日RMSE占实测均值的比例最小,为9.19%。可见,竹林各监测点的预测结果较理想。

表3 茶园验证期实测与预测均值比较Table 3 Comparison of observed and predicated values during validation for tea garden

表4 竹林验证期实测与预测均值比较Table 4 Comparison of observed and predicated values during validation for bamboo forest
通过检验可知,茶园和竹林不同深度,模型均能较为精确地模拟各监测点土壤水分,能很好地反映研究区土壤水的分布状况。因此,以少数典型样点预测研究区土壤水分的分布状态是可行且有效的,为优化研究区域土壤水分的监测,减少野外监测的工作量提供了依据。
2.3.2 不同土地利用方式模拟结果 竹林较茶园具有更好的时间稳定性,监测点土壤水分的相关性更强。由时间稳定性分析结果可知(图1),竹林样点土壤水分较茶园更接近平均土壤水分含量;大部分竹林样点土壤水分相对偏差的标准差较茶园小,时间稳定性较好,而竹林中极少数样点相对偏差的标准差较大,时间稳定性差。同时,由降维因子分析成分图(图2)可知,竹林各监测样点在成分图中呈聚拢形式,而茶园各样点相对分散,竹林土壤水分具有更强的相关性。
在构建线性回归模型时,茶园部分样点与典型样点的相关性较弱,总体决定系数较小,但当添加样点自变量后,决定系数提高较快,总体的模拟效果较好。而竹林大部分样点相关性较强,较少的典型样点即可表达研究区大部分样点,模型决定系数较高;而少数样点相关性弱,时间稳定性差,其预测值与实测值相差较大,造成竹林整体模拟效果差,检验时的RMSE较大。
许多研究者都分析了土壤水分分布的时间稳定性以及影响因素,Gomez-Plaza 等[25]研究发现,当影响因素仅限于地理位置和地形时,土壤水分就呈现出时间上较为稳定的空间分布特征,而当植被也对土壤水分产生影响时,土壤水分在空间上的分布结构就不稳定。本文研究的时间稳定性特征与Gomez-Plaza 等[25]的研究结果一致,茶园和竹林本在地理位置和地形上差异较小,而受到不同类型植被的影响,造成茶园竹林区时间稳定性特征差异较大。
2.3.3 不同深度模拟结果 总体而言,茶园和竹林中大部分 30 cm 深度的模拟结果好于 10 cm 深度(图 4)。这可能是在空间变异结构上 30~40 cm 深度的空间自相关程度高且比较稳定[26],这与潘颜霞等[18]对黄土高原荒漠人工固沙植被区土壤水分时间稳定性研究的结果相一致。此外,表层土壤为降水到达地面时最先承接的部位,其土壤水分变化对降水最为敏感[27-29],土壤水含量波动较大。30 cm 深处,土壤水分空间分布结构相对稳定,但在发生较大降雨量时,也会受到壤中流的影响,空间分布结构局部发生暂时性变化,造成预测效果不理想。
3 结论
1)通过土壤水分时间稳定性结合降维因子分析,选取合理的典型样点组合,应用多元线性回归模型可以有效地预测空间各监测点土壤水分。若仅以时间稳定性为基础选取的样点作为自变量,模型精度不足以精确模拟研究区土壤水分,结合因子分析选取典型样点组合构建模型时,模型模拟精度较高。
2)研究区竹林土壤水分较茶园具有更好的时间稳定性,监测点土壤水分的空间相关性更强。
3)研究区较深层的30 cm土壤水分的空间分布结构较10 cm稳定,土壤水分的分布具有更强的空间变异性。较浅的10 cm深处土壤易受降雨、根系等因素影响,水分波动较大,土壤水分空间分布结构不稳定。
参考文献:
[1]Lin H S.Earth’s critical zone and hydropedology:Concepts characteristics and advances[J].Hydrology and Earth System Sciences,2010,14:25-45
[2]Lin H S,Bouma J,Wilding L P,Richardson J L,Kutilek M.Advances in hydropedology[J].Advances in Agronomy,2005,85:1-89
[3]徐进,徐力刚,丁克强,等.鄱阳湖洲滩湿地土壤-水-植物系统中磷的静态迁移研究[J].土壤学报,2015,52(1):138-144
[4]骆永明,滕应.我国土壤污染退化状况及防治对策[J].土壤,2006,38(5):505-508
[5]林强.我国的土壤污染现状及其防治对策[J].亚热带水土保持,2004,16(1):25-28
[6]Carpenter S R,Caraco N F,Correll D L,et al.Nonpoint pollution of surface waters with phosphorus and nitrogen[J].Ecological Applications,1998,8:559-568
[7]Zhu Q,Schmidt J P,Lin H S,et al.Hydropedological process and their implications for nitrogen availability to corn[J].Geoderma,2009,154:111-122
[8]Serrano J M,Peca J O,da Silva M,et al.Mapping soil and pasture variability with an electromagnetic induction sensor[J].Computers and Electronics in Agriculture,2010,73:7-16
[9]华孟,王坚.土壤物理学[M].北京:北京农业大学出版社,1992
[10]余云飞,许学宏,高芹,等.土壤水分空间分布及时间稳定性的探讨[J].农业环境与发展,2006,23(3):89-92
[11]高晓东,吴普特,张宝庆,等.黄土丘陵区小流域土壤有效水空间变异及其季节性特征[J].土壤学报,2015,52(1):57-67
[12]Berndtsson R,Bahri A,Jinno K.Spatial dependence of geochemical elements in a semiarid agricultural field Geostatistical properties[J].Soil Science Society of America Journal,1993,57:1 323-1 329
[13]朱首军,丁艳芳,薛泰谦,等.农林复合生态系统土壤水分空间变异性和时间稳定性研究[J].水土保持研究,2000,7(1):46-48
[14]Vachaud G,De Silans Passerat A,Balabanis P,et al.Temporal stability of spatially measured soil water probability density function[J].Soil Science Society of America Journal,1985,49:822-827
[15]Burrough P A.Soil variability:A late 20th century view[J].Soils and Fertilizers,1993,56(5):529-562
[16]Brubaker S C,Jones A J,Frank K,et al.Regression models for estimating soil properties by landscape position[J].Soil Science Society of America Journal,1994,58:1 763-1 767
[17]周启友,岛田纯.土壤水空间分布结构的时间稳定性[J].土壤学报,2003,40(5):683-690
[18]潘颜霞,王新平,苏延桂,等.荒漠人工固沙植被区浅层土壤水分动态的时间稳定性特征[J].中国沙漠,2009(1):81-86
[19]邱扬,傅伯杰,王军,张希来,等.土壤水分时空变异及其与环境因子的关系[J].生态学杂志,2007,26(1):100-107
[20]Lin H S,Kogelman W,Walker C,et al.Soil moisture patterns in a forested catchment:A hydropedological perspective[J].Geoderma,2006,131:345-368
[21]Gomez-Plaza A,Alvarez-Rogel J,Albaladejo J,et al.Spatial patterns and temporal stability of soil moisture across a range of scales in a semi-arid environment[J].Hydrological Processes,2000,14:1 261-1 277
[22]杨玉峥,林青,王松禄,等.大沽河中游地区土壤水与浅层地下水转化关系研究[J].土壤学报,2015,52(3):547-557
[23]Reynolds S G.The gravimetric method of soil moisture determination Part Ⅲ.An examination of factors influencing soil moisture variability[J].Journal of Hydrology,1970,11(3):288-300
[24]刘凯,高磊,彭新华,等.半干旱区科尔沁沙地土壤水分时空特征研究.土壤,2015,47(4):765-772
[25]Gomez-Plaza A,Alvarez-Rogel J,Alabal adejo J,et al.Spatial patterns and temporal stability of soil moisture across a range of scales in a semi-arid environment[J].Hydrological Processes,2000 ,14:1 261-1 277
[26]王改改,魏朝富,吕家恪,等.四川盆地丘陵区土壤水分空间变异及其时间稳定性分析[J].山地学报,2009,27(2):211-216
[27]刘宏伟,余钟波,崔广柏.湿润地区土壤水分对降雨的响应模式研究[J].水利学报,2009,40(7):822-829
[28]王峰,沈阿林,陈洪松,等.红壤丘陵区坡地降雨壤中流产流过程试验研究[J].水土保持学报,2007,21(5):15-17,29
[29]Kachanoski R G,Dejong E.Scale dependence and the temporal persistence of spatial patterns of soil water storage[J].Water Resources Research ,1988,24:85-91
Optimizing Soil Moisture Monitoring Based on Temporal Stability and Factor Analysis
LIU Yujiao1,2,ZHU Qing1*,LV Ligang3,LIAO Kaihua1,XU Fei1
(1 Key Laboratory of Watershed Geographic Sciences,Nanjing Instituted of Geographic and Limnology,Chinese Academy of Sciences,Nanjing 210008,China; 2 University of Chinese Academy of Sciences,Beijing 100049,China; 3 School of Geographic and Oceanographic Sciences,Nanjing University,Nanjing 210046,China)
Abstract:This paper armed to optimize soil moisture monitoring by taking hill slopes in a tea garden and a bamboo forest located in Gaochun district of Nanjing City as examples and monitoring soil moisture in long-term.Based on the temporal stability and factor analysis,representative sampling sites were selected to predict soil water contents for other sampling sites by building stepwise regression models,and then checked the predication accuracy.The results showed:when only monitoring soil water content at 7 representative sampling sites in tea garden,RMSE of prediction was ≤1.5 cm3/cm3.In addition,while only monitoring soil water content at 5 representative sampling sites in bamboo forest,RMSE was ≤1.7 cm3/ cm3.This method can reduce the number of soil moisture monitoring sites in predicting soil water content on hill slopes with limit observations.In addition,land use type and soil depth can affect soil moisture characteristics.Bamboo forest had stronger temporal stability and higher spatial autocorrelation in soil moisture than tea garden,however,the performance of regression models for bamboo forest was worse than those for tea garden.It is noted that the spatial structure of soil moisture at 30 cm depth was more stable than that at 10 cm depth,implying the performance of regression models is better at 30 cm than at 10 cm depth.
Key words:Soil water content; Spatial prediction; Temporal stability; Tea garden; Bamboo forest
作者简介:刘玉娇(1991—),女,贵州遵义人,硕士研究生,主要从事土壤水运动模拟研究。E-mail:njuliuyujiao@163.com
* 通讯作者(qzhu@niglas.ac.cn)
基金项目:①国家自然科学基金项目(41271109;41301234)和中国科学院南京地理与湖泊研究所“一三五”重点项目(NIGLAS2012135005)资助。
DOI:10.13758/j.cnki.tr.2016.01.028
中图分类号:S152.7

