数学课堂应如何交给学生——对“基本不等式”一课的教学反思



数学课堂应如何交给学生
——对“基本不等式”一课的教学反思

◇浙江俞一凡

1案例背景

在《基本不等式》一课的比赛课中笔者对在课堂组织过程中教师应何时发挥示范作用,何时把课堂交给学生,如何把课堂交给学生等问题进行了思考．下面就这节比赛课对这几个问题进行探讨和反思．

2课堂回放

教学片断1由赵爽弦图得出不等式a2+b2≥2ab及其等号成立的条件，对其进行证明后提出如下问题.

师:这个重要不等式主要揭示了2个数平方和与2个数乘积之间的不等关系.

用□代替a, △代替b,请你用合适的数或式代入后得到一个你认为成立的不等式．

□2+△2≥2□△.

如果我在□中填入x2,在△中填入y2,那我就得到了这样一个不等式x4+y4≥2x2y2,请问这个不等式等号成立的条件是什么?

生:x2=y2.

师:接下来就请你们试填入数或符号得到新的不等式.

教学片断2已知x>0,y>0,且x+y=1,则1/x+2/y的最小值是________.

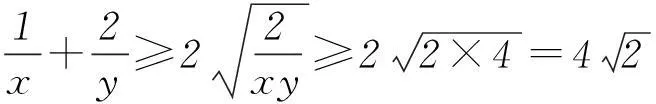
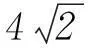
师:请问当x和y分别取什么值的时候能取到这个最小值.

有的学生回答1/x=2/y,有的说x=y,有的说无解.

师:这里用了2次基本不等式,而2个等号成立的条件并不相同,所以导致最终无法取到最小值．

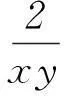
生:一正、二定、三相等,这里的1/x和2/y之积不是定值,所以不符合前提条件,不能这样求解．

师:我们发现这2种错误都是直接对1/x+2/y运用基本不等式,但是忽略了运用基本不等式求最值的前提条件，即必须满足两数之积为定值，和才有最小值,所以我们一起想办法把这个式子变成一个积为定值的式子,我们知道当两数互为倒数时积为定值,那么这里能否出现有倒数形式的两数之和的式子呢?

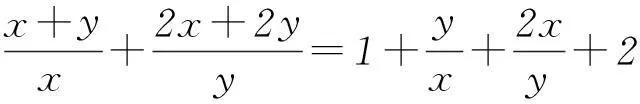
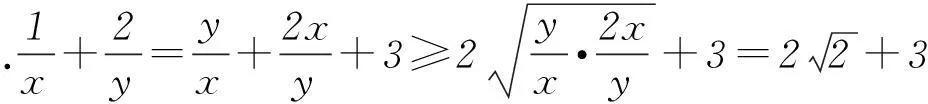
3自我反思

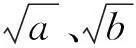
教学片断2中,笔者先是把课堂直接交给学生,因为此时学生已经掌握了利用基本不等式求最值的基本方法,当学生的解答中呈现出一系列错误之后，再加以引导指出学生错解的原因以及“1”的代换法构造积为定值的形式．

4对是否该把课堂交给学生的一点思考

最近,笔者学习了《努力诠释中国特色的数学教育理念以及实践特色》一文, 文中张奠宙教授在谈到接受性学习和探究性学习关系时明确指出:接受性学习和探究性学习所占的时间前者肯定比后者多．张教授给出的理由是：人不能事事都要获得直接经验,大多数时间获得的是间接经验,间接经验就是接受别人转告你的知识而并非亲历．张教授还特别强调了在教学过程中教师的示范很重要,对当前课堂教学中教师作用的弱化表示出很大的遗憾．而现在很盛行的“建构主义”则强调学生对数学概念构造的自我理解,认为教师的主要作用不再是企图去“传递”知识,而是为促进学生心智建构创设学习环境和条件．“建构主义”还认为“反正怎么认识深刻就怎么做,可以不计时间成本”.张教授认为“教学过程是在一定的时间里完成一定的教学任务,需要讲究效率,探究性学习固然可以获得第一手的研究经历,但是需要时间,只能适当进行”．笔者非常同意张教授的观点．

我们应该把课堂交给学生,但是教师的示范作用必不可少．特别是对引言课、新授课要适当减少交给学生的时间.理由很简单,新授课学生基本没有知识基础和研究问题的方法基础,像“集合与函数的概念”“指数函数”“任意角和弧度制”等就属于新授课,主要讲概念及其概念的应用.如果盲目地把课堂交给学生,就会导致浪费时间,教师必须在情境创设、概念的总结及概括上发挥示范作用．当然,在课堂教学中教师需要有对教材所提出的问题很好地进行“理性重建”,融入自己对教材的理解,对所提出的问题要做富有个性化、较为深入的处理,也就是教师只有在做好充分的准备之后才能很好地为学生起到示范作用．所以作为一线教师应该努力提高自己的“数学素养”,了解数学知识的背景,准确把握数学概念、定理、法则、公式等的逻辑意义,深刻领悟讲授内容所反映的思想方法．只有自身的水平提高了,才能在课堂关键处给予学生示范,进而提高课堂效率．

(作者单位：浙江绍兴市第一中学)

下面我们就来进行这个填数游戏: