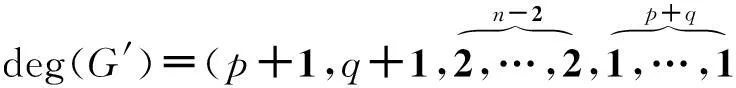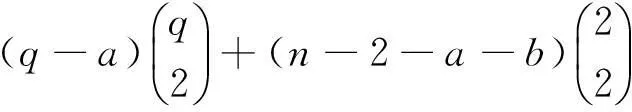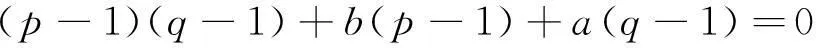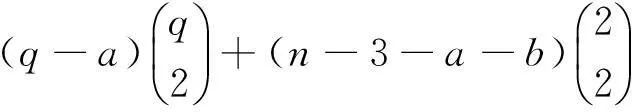似双星树H(p,n,q)由Laplacian谱刻画

卢鹏丽, 刘晓刚

(1.兰州理工大学 计算机与通信学院，甘肃 兰州 730050; 2.墨尔本大学 数学与统计学院，澳大利亚 墨尔本 3010)



似双星树H(p,n,q)由Laplacian谱刻画

卢鹏丽1, 刘晓刚2

(1.兰州理工大学 计算机与通信学院，甘肃 兰州 730050; 2.墨尔本大学 数学与统计学院，澳大利亚 墨尔本 3010)

摘要：似双星树是恰好有两个结点的度大于2的树。用H(p,n,q)表示将路图Pn的两个悬挂点分别与星图S(1,p)及S(1,q)的中心点重合所得到的一类似双星树。首先得到了顶点的度序列，然后由谱性质证明了似双星树H(p,n,q)由Laplacian谱确定，扩大了谱确定图的范围。

关键词：邻接谱；Laplacian谱；A-同谱图；L-同谱图；线图

1基本引理

引理1[13-23]对任意图，由它的邻接谱或Laplacian谱可确定：

1) 结点的个数；

2) 边的条数。

对任意图，由它的邻接谱可确定：

3) 图中任意长度的闭回路的数目。

对任意图，由它的Laplacian谱可确定：

4)图的组成分支数目；

5)生成树的个数；

6)结点度的平方和。

引理2[24]对任意图，长度为4的闭回路的数目等于2倍的边数加上4倍的长度为2的导出路的数目，再加上8倍的长度为4的圈图的数目。

原图G的线图记为(G)。在线图(G)中，其结点相当于原图G的边，当且仅当原图G中的两条边有公共结点时，线图(G)中的结点则为邻接点。

引理3[25]设T是有n个结点的树，(T)是它的线图，则有

式中：i=1,2,…,n-1。

引理4[26]设u是图G的一个结点，从图G中去掉结点u及其结点u的关联边得到子图G-u，有

引理5[2]设e是图G的一条边，从图G中去掉边e得到子图G′=G-e，有

式中：i=1,2,…,m。

引理7[27-28]设图G的结点集V(G)和边集E(G)都不为空，有

式中：mi是图G中所有与结点vi相邻的结点的度的平均值。

引理 8[29]设图G是结点数大于等于3的连通图，则有

引理 9[30]设图G是结点数大于等于4的连通图，则有

2主要结论

似双星树是恰好有两个结点的度大于2的树。将路图Pn的两个悬挂点分别与星图S1,p及S1,q的中心点重合得到的一类似双星树表示为H(p,n,q)，如图1所示，其中p≥q≥1。

图1　似双星树H(p,n,q)Fig.1　The double starlike treeH(p,n,q)

命题1 1) 若n=1，则H(p,n,q)≅K1,p+q且是由Laplacian谱确定的[7]。

2)若n=2或n=3，则H(p,n,q)是由Laplacian谱确定的[31]。

3)若p=q=1，则H(1,n,1)≅Pn+2且是由Laplacian谱确定的[3]。

4)若p>q=1，则H(p,n,1)是似星树且是由Laplacian谱确定的[7]。

5)若p=q≥2，则H(p,n,q)≅Hn(p,p)且是由Laplacian谱确定的[10]。

由命题1知，只需考虑似双星树H(p,n,q)满足n≥4且p>q≥2是否由Laplacian谱确定即可。下面，首先给出似双星图的最大特征根，次大特征根及第三大特征根的界值。

引理10 设G=H(p,n,q)满足n≥4且p>q≥2，则

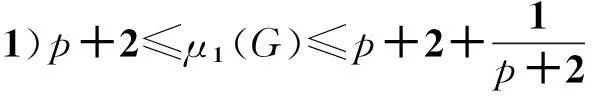
3)μ3(G)<4。

证明：1)由引理7，通过简单的计算即可得到最大特征根的界值。

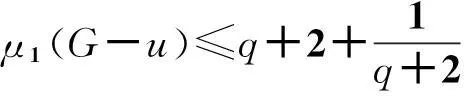
3)删掉Laplacian矩阵L(G)中对应结点u和v的行和列得到(p+n+q-2)×(p+n+q-2)维的主子阵Muv。显然，Muv的最大特征根小于4。由引理6得μ3(G)<4。

引理11 图G=H(p,n,q)满足n≥4且p>q≥2，假设图G′是图G的L-同谱图。那么G′也是似双星树，并且度序列为

证明：由引理1的1)、 2) 、3)和4)知，G′为有n+p+q个结点，n+p+q-1条边的树。设(d1,d2,…,dn+p+q)是图G′的非递增度序列，ni表示图G′中度为i的结点的个数，其中i=1,2,…,d1。

由引理9和引理10的3)可得d3≤μ3(G′)+1=μ3(G)+1<5，进而得d3≤4。

另一方面，由引理1的1)、2)、6)可以得到如下的等式：

(1)

(2)

(3)

综合上述三个等式可以得到

(4)

(5)

上面已经证得d1≤p+1，d2≤q+3和d3≤4。下面分两种情况确定图G′的度序列。

情形 1q=2或q=3。假设d1

(6)

如果q=2，那么就有p≥3。把q=2代入式(6)可以得到p2-3p+6≤0，这与p≥3矛盾。

如果q=3，那么就有p≥4。把q=3代入式(6)可以得到p2-7p+24≤0，这与p≥4矛盾。

经上述讨论知，图G′的结点的最大度d1=p+1，即度为p+1的结点数目np+1≥1。

现在假设np+1≥2，也就是说G′至少存在两个结点的度为p+1。有式(5)可得

如果q=2，由式(5)可得n3=1和ni=0，其中i=4,5,…,p。由式(1)、(2)可得n2=n-2和n1=p+2。由此图G′的度序列为

p3+q3-3p2-3q2+2p+2q

进而可得

(7)

已证得d3≤4， 也就是说，图G′中至多存在两个度大于4的结点，下面从三个方面考虑这个问题。

情形2.1d1=4且d2≤4。由式(7)可得

(8)

把式(8)代入式(4)可得

这与n3≥0矛盾。

情形2.2d1>4且d2=4。由式(7)可得

(9)

把式(9)代入式(4)可得

由d1≤p+1和q≥4可得n3<0，这也与n3≥0矛盾。

情形2.3d1>4且d2>4。由式(7)可得

(10)

把式(10)代入式(4)可得

(11)

已证得了d1≤p+1和d2≤q+3。首先从下面四个方面考虑d1

情形2.3.1 假设d1=p且d2=q+3，由式(10)和(11)可得

(12)

这与n3≥0矛盾。

情形2.3.2 假设d1=p-1且d2=q+3，由式(10)和(11)可得

n3=-3p2+14p-16+3q2-2q=

(13)

由n4≥0得p≥q+2。将p≥q+2代入n3中可得n3≤-q(3q-2)+3q2-2q=0，由此可得p=q+2且n3=n4=0。现有d1=p-1=q+1

情形2.3.3 假设d1≤p-2且d2=q+3，有q+3=d2≤d1≤p-2，即p≥q+5。将d1≤p-2和d2=q+3代入(11)式得

(14)

这也与n3≥0矛盾。

情形2.3.4假设d1≤p且d2≤q+3，由(11)式和p≥q+1得

(15)

由n3=0，得出d1=p，d2=q+2和p=q+1。这时有d1=p=q+1

由上述讨论，可以得到d1=p+1，即np+1≥1。现假设np+1≥2，即图G′中至少存在2个度为p+1的结点。应用式(5)得

进一步得到

这与q

由q≥4，再联合式(10)和(11)得出d2=q+1。由式(5)得，当i=3,4,…,q,q+2,…,p时ni=0。由式(1)和(2)得n1=p+q和n2=n-2，因此得

由此得证。

定理1设图G=H(p,n,q)满足n≥4且p>q≥2，则G由Laplacian谱确定的。

另一方面，容易得到图G的线图(G)的度序列

(16)

简化式(16)得

又p>q≥2，0≤a≤q和0≤b≤p。很容易验证

由此得出矛盾。

图2　G′图Fig.2　The graph G′

再次假设与度为q+1的结点相邻的悬挂点有q-a个，与度为p+1的结点相邻的悬挂点有p-b个，其中a和b是满足0≤a≤q和0≤b≤p的非负整数。通过计算图G和G′中结点的个数，可以到

即

(17)

(18)

简化式(18)得a(q-1)+b(p-1)=0。于是可得a=0和b=0，把a=0和b=0代入式(14)得l1=n。由此可得图G′同构于图G。证明结束。

结合命题1和定理1，有以下结论：

定理2 所有的似双星树H(p,n,q)都是由Laplacian谱确定的。

由于一个图的L谱可以确定它的补图[32]的L谱，那么由定理2可得出下面的结论。

推论 1 任意似双星树H(p,n,q)的补图都是由Laplacian谱确定的。

3结论

1)当p=q时，即图H(p,n,p)是由Laplacian谱确定的。

2)当p≠q时，问题的关键点是确定图的度序列deg(G′)，其中图G′与图H(p,n,q)是L-同谱图。本文在引理3中解决了这个问题，并证明了所有似双星树H(p,n,q)是由Laplacian谱确定的，得到了这个问题的完整解决。

参考文献：

[1]GÜNTHARD H H, PRIMAS H. Zusammenhang von Graphentheorie und Mo-Theorie von Molekeln mit Systemen konjugierter Bindungen[J]. Helvetica Chimica Acta, 1956, 39(6): 1645-1653.

[2]CVETKOVICD, ROWLINSON P, SIMIC S. An introduction to the theory of graph spectra[M]. Cambridge: Cambridge University Press, 2010: 77-89.

[3]VAN DAM E R, HAEMERS W H. Which graphs are determined by their spectrum?[J]. Linear Algebra and its Applications, 2003, 373: 241-272.

[4]AN DAM E R, HAEMERS W H. Developments on spectral characterizations of graphs[J]. Discrete Mathematics, 2009, 309(3): 576-586.

[5]SHEN Xiaoling, HOU Yaoping, ZHANG Yuanping. Graph Zn and some graphs related to Zn are determined by their spectrum[J]. Linear Algebra and its Applications, 2005, 404: 58-68.

[6]WANG Wei, XU Chengxian. Note: the t-shape tree is determined by its Laplacian spectrum[J]. Linear Algebra and its Applications, 2006, 419(1): 78-81.

[7]OMIDI G R, TAJBAKHSH K. Starlike trees are determined by their Laplacian spectrum[J]. Linear Algebra and its Applications, 2007, 422(2/3): 654-658.

[8]BOULET R. The centipede is determined by its Laplacian spectrum[J]. Comptes Rendus Mathematique, 2008, 346(13/14): 711-716.

[9]STANIC Z. On determination of caterpillars with four terminal vertices by their Laplacian spectrum[J]. Linear Algebra and its Applications, 2009, 431(11): 2035-2048.

[10]LIU Xiaogang, ZHANG Yuanping, LU Pengli. One special double starlike graph is determined by its Laplacian spectrum[J]. Applied Mathematics Letters, 2009, 22(4): 435-438.

[11]BU Changjiang, ZHOU Jiang, LI Hongbo. Spectral determination of some chemical graphs[J]. Filomat, 2012, 26(6): 1123-1131.

[12]AALIPOUR G, AKBARI S, SHAJARI N. Laplacian spectral characterization of two families of trees[J]. Linear and Multilinear Algebra, 2014, 62(7): 965-977.

[13]BOULET R, JOUVE B. The lollipop graph is determined by its spectrum[J]. The Electronic Journal of Combinatorics, 2008, 15(1): 74.

[14]BOULET R. Spectral characterizations of sun graphs and broken sun graphs[J]. Discrete Mathematics and Theoretical Computer Science, 2009, 11(2): 149-160.

[15]CVETKOVIC D M, DOOB M, SACHS H. Spectra of graphs: theory and applications[M]. New York, San Francisco: Academic Press, 1980: 50-53.

[16]HAEMERS W H, LIU Xiaogang, ZHANG Yuanping. Spectral characterizations of lollipop graphs[J]. Linear Algebra and its Applications, 2008, 428(11/12): 2415-2423.

[17]LIU Xiaogang, WANG Suijie. Laplacian spectral characterization of some graph products[J]. Linear Algebra and its Applications, 2012, 437(7): 1749-1759.

[18]LIU Muhuo, LIU Bolian. Some results on the Laplacian spectrum[J]. Computers & Mathematics with Applications, 2010, 59(11): 3612-3616.

[19]LU Pengli, LIU Xiaogang, YUAN Zhanting, et al. Spectral characterizations of sandglass graphs[J]. Applied Mathematics Letters, 2009, 22(8): 1225-1230.

[20]MIRZAKHAH M, KIANI D. The sun graph is determined by its signless Laplacian spectrum[J]. Electronic Journal of Linear Algebra, 2010, 20: 610-620.

[21]WANG Jianfeng, HUANG Qingxiang, BELARDO F, et al. On the spectral characterizations of ∞-graphs[J]. Discrete Mathematics, 2010, 310(13/14): 1845-1855.

[22]ZHOU Jiang, BU Changjiang. Laplacian spectral characterizaiton of some graphs obtained by product operation[J]. Discrete Mathematics, 2012, 312(10): 1591-1595.

[23]SILVA OLIVEIRA C, DE ABREU N M M, JURKIEWILZ S. The characteristic polynomial of the Laplacian of graphs in (a, b)-linear classes[J]. Linear Algebra and its Applications, 2012, 356(1/3): 113-121.

[24]CVETKOVIC D, ROWLINSON P. Spectra of unicyclic graphs[J]. Graphs and Combinatorics,1987, 3(1): 7-23.

[25]GUTMAN I, GINEITYTE V, LEPOVIC M, et al. The high-energy band in the photoelectron spectrum of alkaners and its dependence on molecular structure[J]. Journal of the Serbian Chemical Society, 1999, 64(11): 673-680.

[26]LOTKER Z. Note on deleting a vertex and weak interlacing of the Laplacian spectrum[J]. Electronic Journal of Linear Algebra, 2007, 16(1): 68-72.

[27]KELMANS A K, CHELNOKOV V M. A certain polynomial of a graph and graphs with an extremal numbers of trees[J]. Journal of Combinatorial Theory, Series B, 1974, 16(3): 197-214.

[28]LI Jiongsheng, ZHANG Xiaodong. On the Laplacian eigenvalues of a graph[J]. Linear Algebra and its Applications, 1998, 285(1/3): 305-307.

[29]LI Jiongsheng, PAN Yongliang. A note on the second largest eigenvalue of the Laplacian matrix of a graph[J]. Linear and Multilinear Algebra, 2000, 48(2): 117-121.

[30]GUO Jiming. On the third largest Laplacian eigenvalue of a graph[J]. Linear and Multilinear Algebra, 2007, 55(1): 93-102.

[31]沈小玲, 侯耀平. 一些由它的Laplacian谱确定的树[J]. 湖南师范大学: 自然科学学报, 2006, 29(1): 21-24, 46.

SHEN Xiaoling, HOU Yaoping. Some trees are determined by their Laplacian spectra[J]. Journal of Natural Science of Hunan Normal University, 2006, 29(1): 21-24, 46.

Double starlike treeH(p,n,q) determined by Laplacian spectrum

LU Pengli1，LIU Xiaogang2

(1. School of Computer and Communication, Lanzhou University of Technology, Lanzhou 730050, China; 2. Department of Mathematics and Statistics, The University of Melbourne, Melbourne 3010, Australia)

Abstract：A tree is called double starlike if it has exactly two vertices of degree greater than two. Let H(p,n,q) denote a class of double starlike tree obtained from two stars S(1,p) and S(1,q) by identifying the center of S(1,p)with one end of Pn and the center of S(1,q) with the other end of Pn. First, we get the degree sequence of vertices. Then, by using spectral properties, it is proved that all double starlike trees H(p,n,q) are determined by their Laplacian spectra, which enlarges the scope of graphs determined by their spectra.

Keywords：adjacency spectrum; Laplacian spectrum; A-cospectral graphs; L-cospectral graphs; line graph

中图分类号：O157.5, O157.6

文献标志码：A

文章编号：1006-7043(2016)02-0242-06

doi:10.11990/jheu.201409027

作者简介：卢鹏丽(1973-)， 女，教授.通信作者：卢鹏丽，E-mail：lupengli88@163.com.

基金项目：国家自然科学基金资助项目(11361033).

收稿日期：2014-09-09.网络出版日期：2015-12-15.

网络出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20151215.1030.008.html