圆锥环境作为姿态算法优化环境的适用性分析

蒋郡祥,于飞

(1.哈尔滨工程大学 自动化学院, 黑龙江 哈尔滨 150001; 2.哈尔滨工程大学 理学院, 黑龙江 哈尔滨 150001)



圆锥环境作为姿态算法优化环境的适用性分析

蒋郡祥1,于飞2

(1.哈尔滨工程大学 自动化学院, 黑龙江 哈尔滨 150001; 2.哈尔滨工程大学 理学院, 黑龙江 哈尔滨 150001)

摘要：由于圆锥环境的运动形式过于简单，使得基于其获得的优化系数在实际运动环境中应用的适用性受到质疑。针对上述问题，采用无穷项傅里叶级数展开的方法描述了载体的实际运动环境，基此对姿态算法相关公式进行了重新推导，并得出了相应的姿态算法优化系数，在理论上证明了圆锥环境可以作为姿态算法优化环境。证明了增加姿态算法的子样数，提高陀螺仪的采样频率可以有效抑制姿态算法解算误差。仿真结果表明了相关结论的正确性。

关键词：圆锥环境；捷联惯性导航系统；姿态算法；傅里叶级数；优化系数

捷联惯性导航系统(strapdown inertial navigation system, SINS)的惯性器件量测单元刚性固联在载体上。陀螺仪量测的角运动的动态范围较大，转动的不可交换性体现明显，导航计算机需要通过合适的方式处理量测数据，获得捷联姿态矩阵。姿态算法的目的即在于优化捷联姿态矩阵计算过程中的相关系数，以期得到更加准确的捷联姿态矩阵。

Bortz[1]首先推导得到了旋转矢量的微分方程，同时提出了一种旋转矢量已知的周期性的载体运动形式，即圆锥环境。Bortz提出这种圆锥环境的最初目的是圆锥环境的旋转矢量已知，可以在姿态算法计算机仿真时用于算法的精度分析，并没有说明这种运动环境可以用于姿态算法的系数优化。Miller[2]在Bortz研究的基础上，基于旋转矢量微分方程设计出二子样、三子样姿态算法，并利用圆锥环境对算法的系数进行了优化，这也是首次有学者利用圆锥环境作为姿态算法相关系数的优化环境，类似的算法也得到了进一步的发展[3-8]。但是，这些文章都没有对圆锥环境作为优化环境的适用性进行合理的分析说明。而且圆锥环境相比于载体的实际运动环境，其运动形式过于简单，基于圆锥环境优化的系数在实际环境中的表现受到质疑。

针对这一问题，本文假设惯性器件为理想器件，即量测无误差且传递函数幅频与相频特性不计[9-10]，利用无穷项傅里叶级数描述载体实际运动环境，在这种环境下对姿态算法的相关公式进行重新推导，并对相关系数进行了优化，推导更具有普适性的优化系数。

通过对比2种环境下的姿态算法相关公式和优化系数，以分析圆锥环境作为姿态算法优化环境的适用性，如此便可以通过运动形式非常简单的圆锥环境完成各子样姿态算法的系数优化。通过实际运动环境对应的姿态算法相关公式，可以更加直观地对解算误差进行分析，得出陀螺仪的量测精度与采样速率越高解算误差越小这一结论。最后，通过计算机仿真验证了相关结论的正确性。

1傅里叶级数表达的载体运动环境

对于圆锥环境，其形式相对于载体的实际运动情况过于理想化，基于典型圆锥环境的相关系数优化过程难以使人信服。以下即是人为设定的载体运动圆锥环境的旋转矢量以及相应的载体运动角速度：

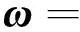
(1)

对应的在环境进行的算法设计及其系数优化过程[2-8]，本文将不再重述。

本文通过傅里叶级数形式表达了载体的实际运动形式。设捷联惯性导航系统(strapdown inertial navigation system，SINS)完成初始对准后，进入导航状态的时刻为ton，SINS退出导航状态的时刻为toff。在此期间内，载体相对于惯性空间的角运动数据用以下函数形式表示:

(2)

以ω(t)的形式在整个时间域内进行周期性延拓，得其延拓形式为

(3)

将式(2)通过傅里叶级数的形式展开为

(4)

2姿态算法相关公式的重新推导

对于基于旋转矢量的姿态算法而言，其数学本质就是利用陀螺仪量测数据更加精确地求解旋转矢量微分方程。其中旋转矢量的微分方程[1]如下:

(5)

由于SISN的姿态信息更新频率较快，单个更新周期内的旋转矢量的幅值并不是很大，其第三项一般可以忽略。在等式右侧用θ代替φ得到旋转矢量微分方程的一阶近似表达式[9]为

(6)

式中：θ=∫ωdt。

对式(6)在更新区间t∈(tm-1,tm)内做积分，获得本更新区间的旋转矢量为

(7)

式中：θ(tm,tm-1)被称为旋转项，数值等于在一个更新周期内激光陀螺仪输出的角增量相加，精度取决于采样精度与A/D的字长，偏差一般可以忽略不计[11]。β(tm,tm-1)被称为旋转补偿项，其数值包含了ω方向改变而引入的误差，在算法设计过程中要重点补偿，表达式为[11]

(8)

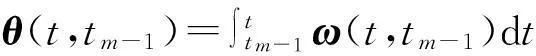
(9)

将式(4)与式(9)代入式(8)中，可以得到旋转补偿项在本文所提用无穷项傅里叶级数描述的载体实际运动环境下的x轴分量真值为

(10)

其中,H=tm-tm-1为更新周期。

通过式(10)可以发现，当i≠j时，其连加项为周期分量，误差不会随时间“累积”。当i=j时，其连加项为“直流”分量与周期分量的叠加形式，若不对直流分量加以补偿，由此引起的误差会随时间累积，导致偏差愈来愈大。当i=j时，其旋转补偿项x轴向直流分量如下:

(11)

同理，可以对应写出其y, z轴向分量为

(12)

(13)

则旋转补偿项直流分量真值为

(14)

旋转补偿项的计算值是通过角增量叉乘，然后相加的形式[3]近似获取，以三子样Miller姿态算法[2]为例:

(15)

(16)

2个不同采样周期角增量叉乘项的x轴分量如下：

(17)

通过式(17)可以发现，当i≠j时，其连加项为周期分量。当i=j时，其连加项为“直流”分量与周期分量的叠加，利用此直流分量对旋转补偿项真值中的直流分量加以补偿。可以得到当i=j时的旋转补偿项直流分量的计算值为

(2b-4a)sin(2Ωih)+2asin(3Ωih))

(18)

对式(14)、(18)进行泰勒级数展开

(19)

(20)

Miller姿态算法的相关系数优化思路就是对直流分量加以补偿，为使式(19)、(20)的直流分量尽可能接近，使泰勒展开后连加项中的前两项对应相等，得到

(21)

解得a=0.450 0,b=1.350 0，这与Miller的三子样姿态算法[2]优化后的系数一致。观察式(14)与式(18)可以发现，旋转矢量真值与计算值各轴分量中同频率直流分量具有相同的系数形式，而且不同频率对应的直流分量相互解耦。因此，不同频率对应直流分量具有相同的优化系数且与相位无关，圆锥环境相当于相位固定的单一频率对应的载体运动环境。由此可以得出如下结论，对于那些与Miller姿态更新算法有相同思路的算法(各子样姿态算法)，可以通过典型圆锥环境进行系数优化。

HPLC-MS/MS法测定人血浆中地佐辛的浓度及其应用……………………… 崔志敏，王逸雅，焦菲菲，等（1·14）

3误差分析

通过式(19)、(20)可以发现，利用泰勒级数展开式进行旋转补偿项直流分量补偿时，只做到了前两项相等(L=3时)，对于其后的无穷多项，根据傅里叶级数的收敛性可知，一定存在某一正整数Num，当i,j≥Num时其幅值工程上可以忽略不计[12]，但数值上依然会随时间累计。此类姿态算法在设计之初并没有考虑周期分量的补偿问题。虽然误差的周期性分量不会随时间累积，但是某一时刻周期性分量的绝对误差依然存在。同样应该注意到泰勒级数的基频周期为toff-ton，时间很长，误差的周期性分量需要极长的时间才能做到累积为零。因此需要想办法对其加以抑制，削弱周期分量的幅值。旋转补偿项解算误差可以表示为

(22)

(23)

因此，提高陀螺仪采样频率可以有效地遏制误差的周期性分量幅值。

4仿真分析

为了更好地体现载体运动环境对旋转补偿项周期分量幅值及直流分量补偿精度的影响，仿真环境保留式(4)中傅里叶级数的常数项及前三个周期项，幅值和相位各异。根据式(16)得出起始时刻为tm-1的更新周期内第n个陀螺仪采样值：

(24)

式中：常数项在区间(0.1°～0.2°)内任意取值。周期项幅值(Pi,Qi,Ri,i=1,2,3)在区间(0.01°～0.05°)内任意取值。为使载体运动的周期项影响更加明显，取基频fbase=1Hz，基频的选取不会影响旋转补偿项周期性误差分量幅值及直流分量补偿误差随fbase/fupdate的变化趋势。更新频率:

fupdate=1H=1Lh=fsampleL

(25)

式中：fsample=1/h为采样频率。

通过计算机仿真得到6组关于载体横摇(roll)、纵摇(pitch)，及航向(yaw)误差的周期分量均方根和60s直流分量补偿误差累积与fbase/fupdate的关系图，如图1～6所示。仿真结果纵轴数值与仿真环境数值的选取有关，没有参考价值，但误差的变化趋势与实际相符。

可以发现，各轴向误差的变化趋势一致，即误差的绝对值随fbase/fupdate的增大而单调增加。当更新频率fupdate相同时，四子样算法(L=4)的误差要比三子样算法(L=3)的误差小。此时，四子样算法对应的陀螺仪采样频率fsample高于三子样算法。当子样数L相同时，误差随fbase/fupdate减小而减小。即，误差随着陀螺仪采样频率fsample的增加而减小。综上所述，若想切实提高SISN的姿态解算精度，要在保证陀螺仪采样精度的前提下，提高采样频率。

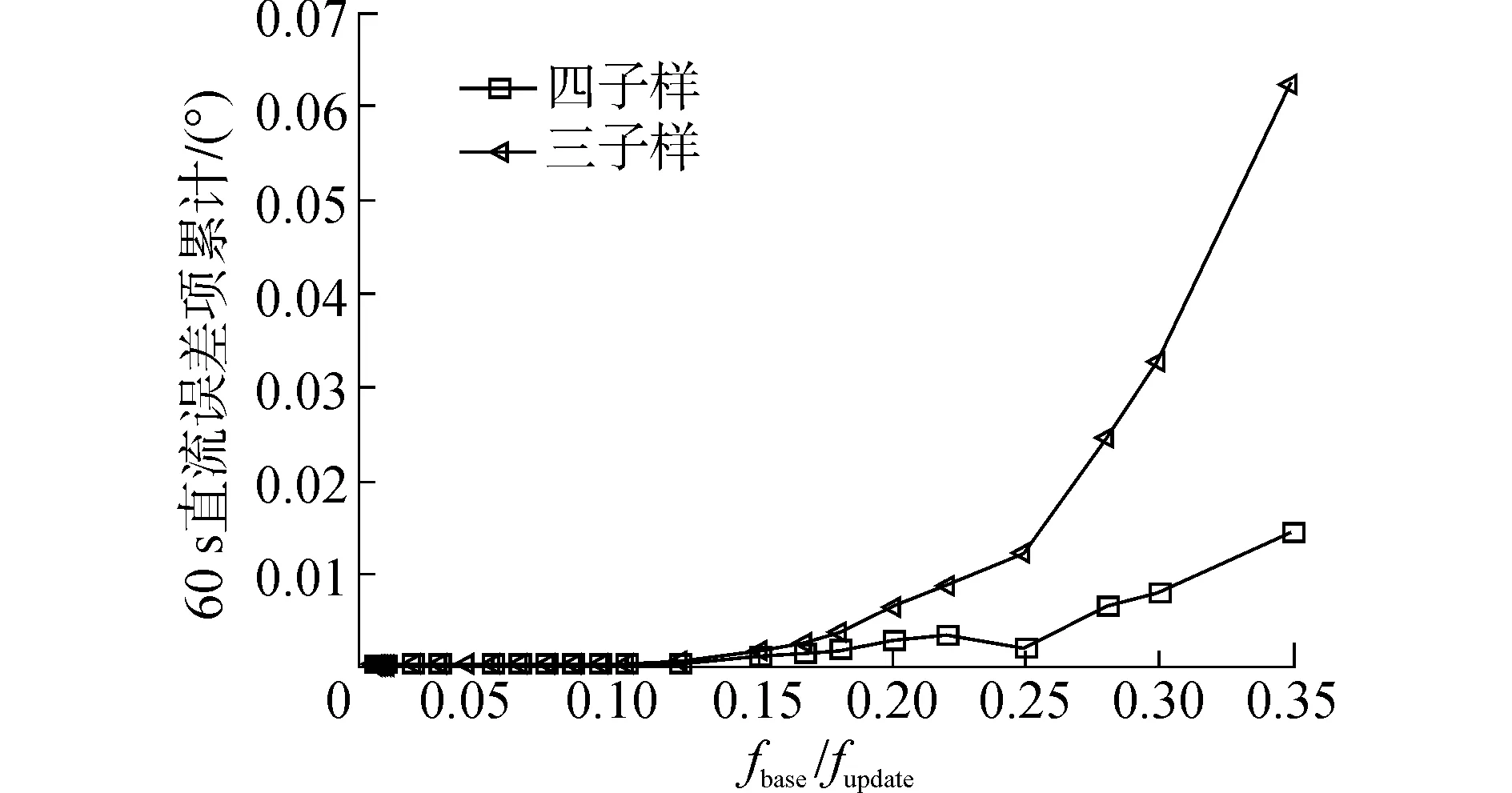
图1　航向直流误差项累积Fig.1　Cumulative DC error of yaw

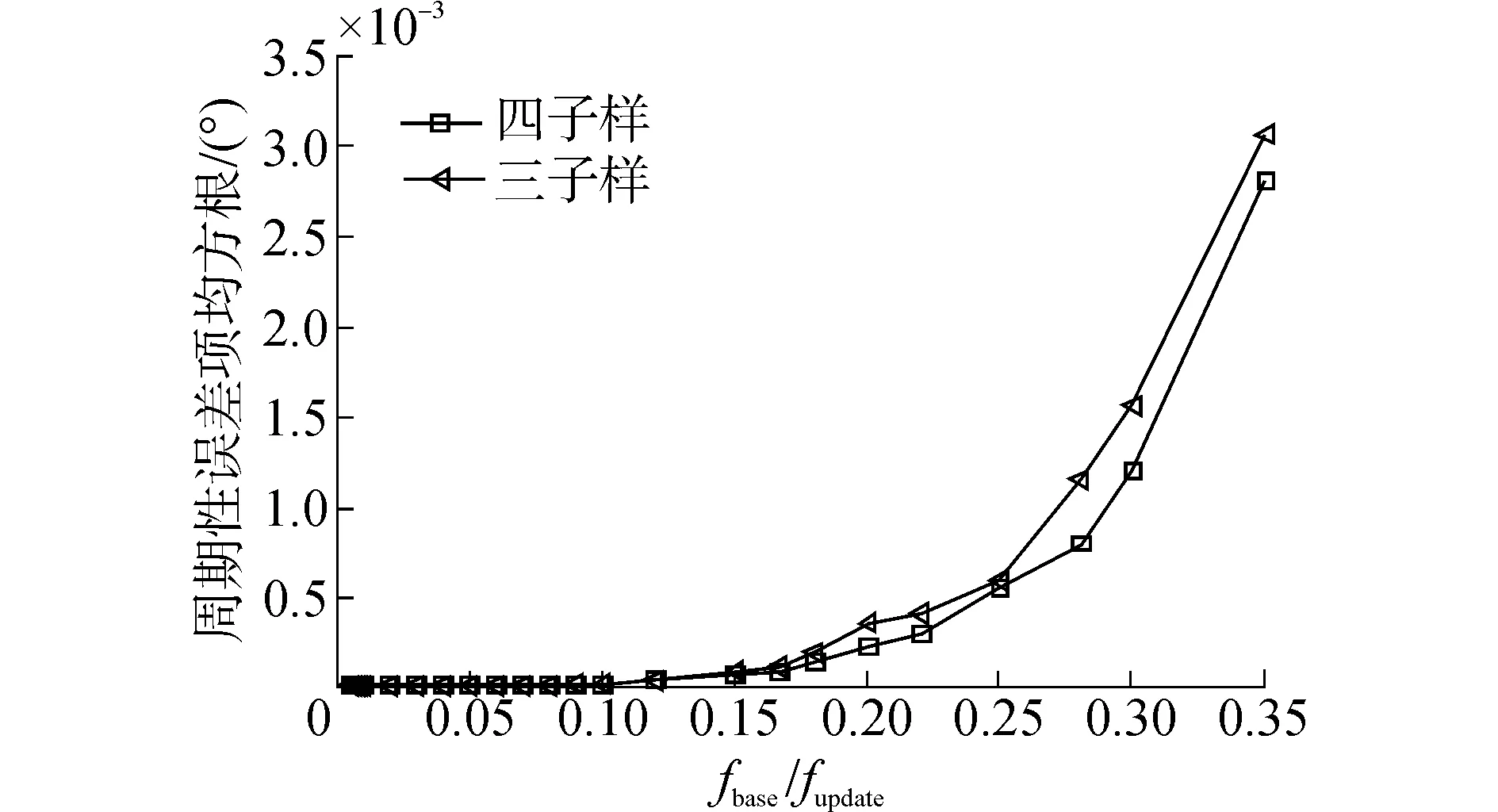
图2　航向周期误差项均方根Fig.2　Periodic error′s RMS of yaw

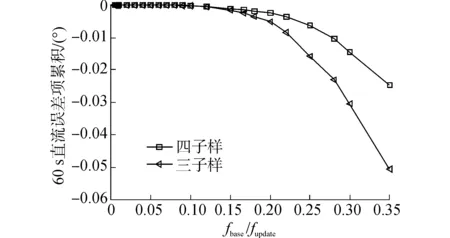
图3　纵摇直流误差项累积Fig.3　Cumulative DC error of pitch

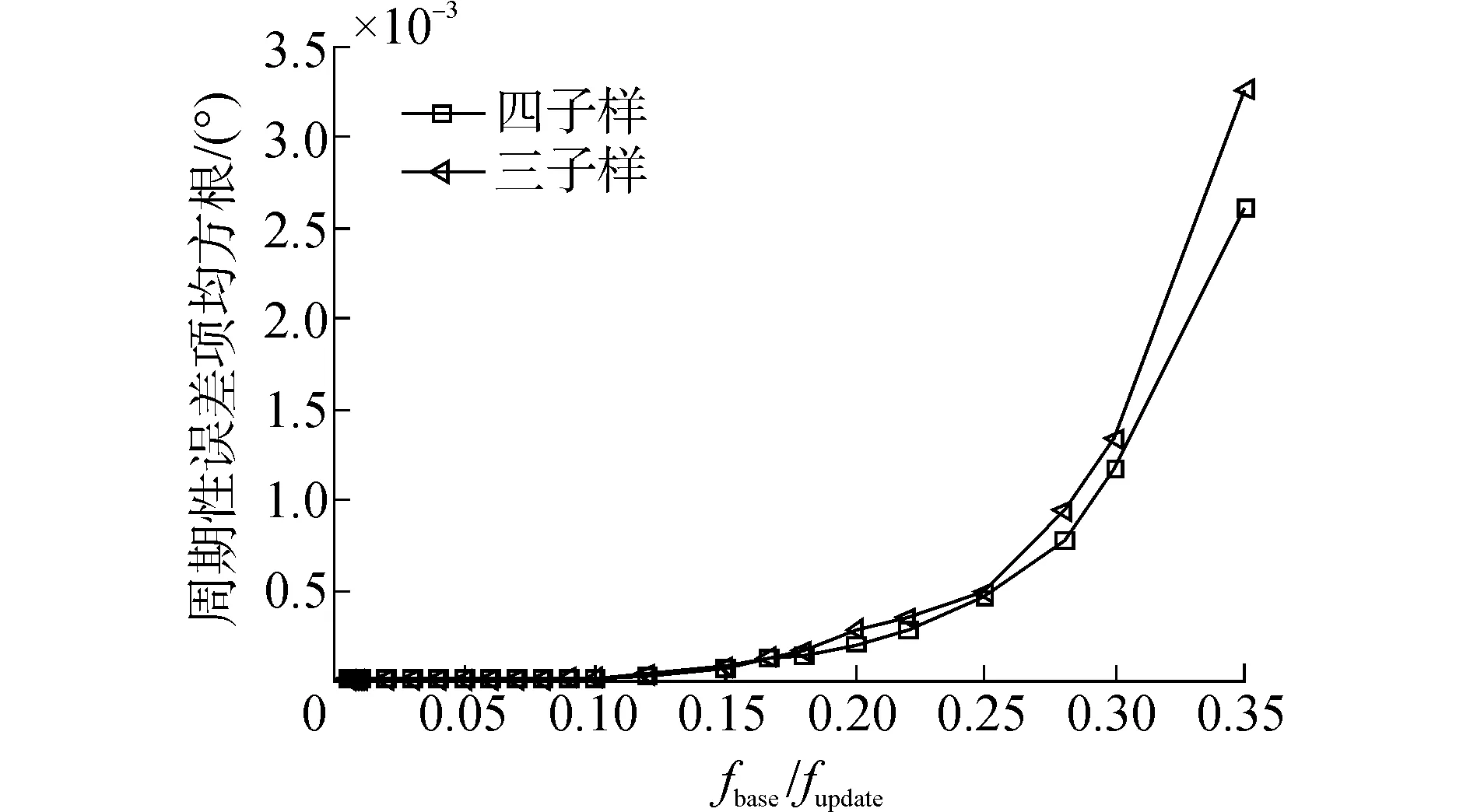
图4　纵摇周期误差项均方根Fig.4　Periodic error′s RMS of pitch

图5　横摇直流误差项累积Fig.5　Cumulative DC error of roll

图6　横摇周期误差项均方根Fig.6　Periodic error′s RMS of roll

5结论

1)本文的系数优化可以认为是基于实际环境进行的。通过这种方式证明了圆锥环境在姿态算法系数优化中的适用性，为圆锥环境在各子样姿态算法中的应用提供了理论基础。但是，这种方法也无法通过算法上的改进对姿态解算中的周期性误差进行抑制，这是一个值得深入思考的问题。

2)通过研究发现，在保持陀螺仪采样精度的前提下，提高陀螺仪的采样频率可以在一定程度上抑制周期性误差项。因此，高性能的陀螺仪在捷联惯性导航系统的姿态解算精度方面起到至关重要的作用。

参考文献：

[1]BORTZ J E. A new mathematical formulation for strapdown inertial navigation[J]. IEEE transactions on aerospace and electronic systems, 1971, 7(1): 61-66.

[2]MILLER R B. A new strapdown attitude algorithm[J]. Journal of guidance, control, and dynamics, 1983, 6(4): 287-291.

[3]IGNAGNI M B. Optimal strapdown attitude integration algorithms[J]. Journal of guidance, control, and dynamics, 1990, 13(2): 363-369.

[4]MUSOFF H, MURPHY J H. Study of strapdown navigation attitude algorithms[J]. Journal of guidance, control, and dynamics, 1995, 18(2): 287-290.

[5]BEN Yueyang, SUN Feng, GAO Wei, et al. Generalized method for improved coning algorithms using angular rate[J]. IEEE transactions on aerospace and electronics systems, 2009, 45(4): 1565-1572.

[6]LI Zongtao, WU Tiejun, MA Longhua. A coning compensation algorithm for SINS in high dynamic motion[J]. Journal of control engineering and applied informatics, 2011, 13(3): 32-40.

[7]IGNAGNI M. Optimal sculling and coning algorithms for analog-sensor systems[J]. Journal of guidance, control, and dynamics, 2012, 35(3): 851-860.

[8]FU Li, WANG Lingling, HU Jianghai. Coning algorithm based on singular perturbation[J]. Aircraft engineering and aerospace technology, 2013, 85(3): 178-185.

[9]SAVAGE P G. Strapdown sculling algorithm design for sensor dynamic amplitude and phase-shift error[J]. Journal of Guidance, Control, and Dynamics, 2012, 35(6): 1718-1729.

[10]MARK J G, TAZARTES D A. Tuning of coning algorithms to gyro data frequency response characteristics[J]. Journal of guidance, control, and dynamics, 2001, 24(4): 641-647.

[11]SAVAGE P G. Strapdown inertial navigation integration algorithm design part 1: Attitude algorithms[J]. Journal of guidance, control, and dynamics, 1998, 21(1): 19-28.

[12]BOGGESS A, NARCOWICH F J. A first course in wavelets with Fourier analysis[M]. 2nd ed. Hoboken: John Wiley and Sons, 2009: 129-133.

[13] SAVAGE P G. Explicit frequency-shaped coning algorithms for pseudo coning environments[J]. Journal of guidance, control, and dynamics, 2011, 34(3): 774-782.

[14]PATERA R P. Attitude propagation for a slewing angular rate vector[J]. Journal of guidance, control, and dynamics, 2010, 33(6): 1847-1855.

Analysis of applicability of cone environment as optimization environment of attitude algorithm

JIANG Junxiang1，YU Fei2

(1.College of Automation, Harbin Engineering University, Harbin 150001, China; 2. College of Science, Harbin Engineering University, Harbin 150001, China)

Abstract：Since the movement form in a cone environment is too simplistic, the applicability of an optimization coefficient based on this movement is questionable for a real movement environment. In this regard, we describe the real movement environment of a carrier using a method based on an infinite Fourier series. We carry out a new derivation for formulas related to the attitude algorithm, and obtain the corresponding optimization coefficient of the attitude coefficient, which theoretically proves that the cone environment can be used as the optimization environment of the attitude algorithm. We prove that increasing the sample number of the attitude algorithm and increasing the sampling frequency of the gyroscope can effectively reduce the calculation error of the attitude algorithm. Lastly, our simulation results validate the above conclusion.

Keywords：coning environment; strapdown inertial navigation system; attitude algorithm; Fourier series; optimized coefficient

中图分类号：U666.1

文献标志码：A

文章编号：1006-7043(2016)02-0231-06

doi:10.11990/jheu.201411009

作者简介：蒋郡祥(1991-), 男, 硕士研究生;通信作者：蒋郡祥，E-mail:1505920735@qq.com.

基金项目：国家自然科学基金资助项目 (51379047，51379042).

收稿日期：2014-11-03.网络出版日期：2015-12-15.

网络出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20151215.1517.034.html

于飞(1974-), 男, 教授, 博士生导师.