介质散射的双线性高阶叠层基函数矩量法分析

樊振宏　何姿　陈如山

(南京理工大学通信工程系,南京 210094)



介质散射的双线性高阶叠层基函数矩量法分析

樊振宏何姿陈如山

(南京理工大学通信工程系,南京 210094)

摘要提出了一种基于双线性思想的高阶基函数降低矩量法分析介质目标电磁散射问题时的未知量.论文给出了双线性高阶叠层基函数的构造过程,并将其应用于介质的面积分方程分析中. 数值算例比较了不同阶数时所需未知量以及计算精度,表明该高阶叠层基函数在满足相同积分方程的计算精度时能比低阶基函数节省未知量.

关键词电磁散射;高阶基函数;矩量法

DOI10.13443/j.cjors.2015040301

MoM analysis on the electromagnetic scattering of dielectric object by using high order bilinear basis function

FAN ZhenhongHE ZiCHEN Rushan

(DepartmentofCommunicationEngineering,NanjingUniversityofScienceandTechnology,Nanjing210094,China)

Abstract High order hierarchical bilinear basis function is proposed to reduce the number of unknowns for the method of moments(MoM) analysis on the electromagnetic scattering of dielectric objects. It combines higher-order vector basis function with bilinear basis function, and is employed to solve the Poggio-Miller-Chang-Harrington-Wu-Tsai (PMCHWT) equation. The number of unknowns and the accuracy are compared between the new basis functions with different orders. Numerical examples show that the proposed method requires relatively less unknowns than the conventional method, and can obtain the same precision.

Keywords electromagnetic scattering; higher order basis function; method of moments

引言

近年来,由于隐身技术以及电磁防护的需要,非导体材料在工程中得到大量应用,介质目标的电磁散射特性分析受到越来越多的重视. 对于介质目标的电磁散射分析,目前主要是利用矩量法分析介质表面Poggio-Miller-Chang-Harrington-Wu-Tsai (PM-CHWT)方程. 传统的矩量法使用定义在子区域的低阶线性基函数来逼近待求的表面电流密度和磁流密度,比如平面Rao-Wilton-Glisson (RWG)基函数[1]．在分析电大尺寸目标电磁散射特性时,需要的基函数个数比较多,消耗较多的计算机资源. 高阶基函数技术可以缓解这一困难,近年来得到大量研究. 高阶基函数技术主要分为两类:插值型高阶基函数与叠层型高阶基函数[2-4]．前者每一个组成基函数的阶次都一样高,而对于后者,任意的第M阶基函数都是第M+l阶基函数的子集,它是通过低阶和高阶的混合来构造出与插值型高阶基函数同样空间模拟能力的基函数. 后者由于具有叠层性在分析中有更多的灵活性. 现阶段采用的高阶基函数,通常对于一个M阶的基函数系统,基函数法向分量的阶数为M阶,切向分量为M-1阶. 比如RWG基函数,它属于法向线性/切向常量(Linear Norm/Constant Tangential, LN/CT)基函数,即法向分量为1阶,切向分量为0阶,所以有些文献将它称为0.5阶基函数[2]. 文献[5-6]提出了一种平面剖分的法向线性/切向线性(Linear Norm/Linear Tangential, LN/LT)基函数,称为LL基函数,本文又称之为双线性基函数. LL基函数在所定义的棱边上切向分量与法向分量对应的多项式阶数一样高,均为1阶.它比RWG基函数的优势在于其对复杂函数的逼近能力更强,三角形剖分形状对其分析精度影响小.文献[6]发现LL基函数能高精度分析磁场积分方程. 本论文将这一思想推广到高阶情况,即对于一个M阶的叠层基函数系统,所构造的基函数的法向分量和切向分量的最高阶数均为M阶. 下面将介绍这一基函数的构造及其在PMCHWT积分方程中的应用. 给出的数值算例表明采用双线性思想的高阶叠层基函数能够在满足相同计算精度的同时减少未知量.

1PMCHWT积分方程

根据均匀介质目标内外表面的散射场、总场及入射场的关系,可建立PMCHWT方程:

[L1(J)+K1(M)]-[L2(-J)+K2(-M)]|tan

=Einc(r)|tan,

(1)

[P1(J)+Q1(M)]-[P2(-J)+Q2(-M)]|tan

=Hinc(r)|tan.

(2)

式中: Einc,Hinc表示入射波的电场强度与磁场强度； J和M表示介质表面等效电、磁流； 下标tan表示取切向分量； 下标1和2表示介质外空间和介质内区域； 算子L,K,P,Q的表达式如下：

Lm(X)=jωμm∫T′Gm·XdS′-

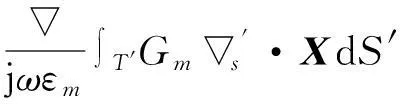
Km(X)=∫T′Gm×XdS′，

Pm(X)=-∫T′Gm×XdS′，

Qm(X)=jωεm∫T′Gm·XdS′-

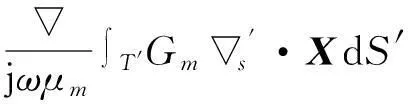
Gm为对应区域空间格林函数,

(3)

εm、μm和km分别表示对应区域空间介质的介电常数、磁导率和波数,ω表示入射电磁波的角频率，R=|r-r′|表示观察点r与源点r′之间的距离.

2双线性高阶叠层基函数

选取曲面三角形对目标表面进行几何建模[7],为了方便计算,将之转换到标准参数空间坐标系中,如图1所示. 图1中左边图形表示实际空间坐标系下的曲面三角形,数字1、2、3表示曲面三角形的3个顶点,4、5、6表示三条曲线边的中点, ri(i=1, 2, …, 6)分别表示它们的坐标. 右边图形表示对应的参数空间坐标系三角形,ξ1,ξ2为参数空间坐标系中的两个参量,ξ3=1-ξ1-ξ2. 空间中的任意一点r可用参数坐标表达为

(4)

式中φi(ξ1,ξ2)是形函数,其表达式可参考文献[7].

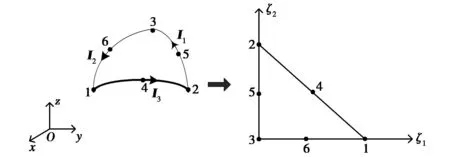
图1　曲面三角形及其投影的参数空间

在观察曲三角形单元内,第1,2类1阶曲面双线性基函数的表达式如下:

(5)

(6)

J为转换过程的雅可比因子(Jacobian),表达式为

(7)

表1三角形单元上基于棱边的和面的3阶多项式

基于棱边的多项式基于面的多项式E1β=3P1(ξβ+1-ξβ+2)F0,1β=23ξβE2β=5P2(ξβ+1-ξβ+2)F0,2β=23ξβ(5ξβ-3)F1,1β=65ξβ(ξβ+1-ξβ+2)E3β=7P3(ξβ+1-ξβ+2)F0,3β=230ξβ(7ξ2β-8ξβ+2)F1,2β=230(7ξ2β-3ξβ)(ξβ+1-ξβ+2)F2,1β=2210ξβ(ξ2β+1-4ξβ+1ξβ+2+ξ2β+2)

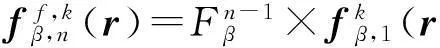
(8)

矩量法分析时首先将介质表面等效电磁流J和M用基于双线性思想的高阶基函数展开为:

(9)

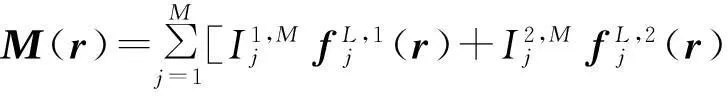
(10)

(11)

计算式(11)中矩阵元素需要知道基函数的面散度,可参考文献[7]中的计算方式. 求解式(13)得出等效电磁流之后,可经过后处理计算出远区散射场Esc,得到雷达散射截面(Radar Cross-Section, RCS):

(12)

3数值算例

算例1是一个半径为1.0m的介质球,介质的相对介电常数为2.0,平面波的入射角度为θi=0°, φi=0°,频率为300MHz. 观察φ=0°平面随θ变化的双站RCS[10](VV极化). 在介质面上建立PMCHWT方程. 图2给出了不同阶数时基于双线性思想的高阶基函数的PMCHWT方法和Mie级数解析解[11]的RCS计算结果对比,可以看出,不同阶数时基于双线性思想的高阶基函数的PMCHWT方法的结果是吻合的. 表2则给出了各个阶数的基函数下剖分尺寸和未知量数,可以看出,阶数高的时候可采用大的剖分尺寸,减少未知量,同时满足积分方程精度.验证了基于双线性思想的高阶基函数方程的正确性.

图2　算例1双站RCS计算结果对比

表2算例1各阶数下方程计算时的剖分尺寸和未知量

阶数剖分尺寸/m未知量10.1770420.25400030.37394840.454464

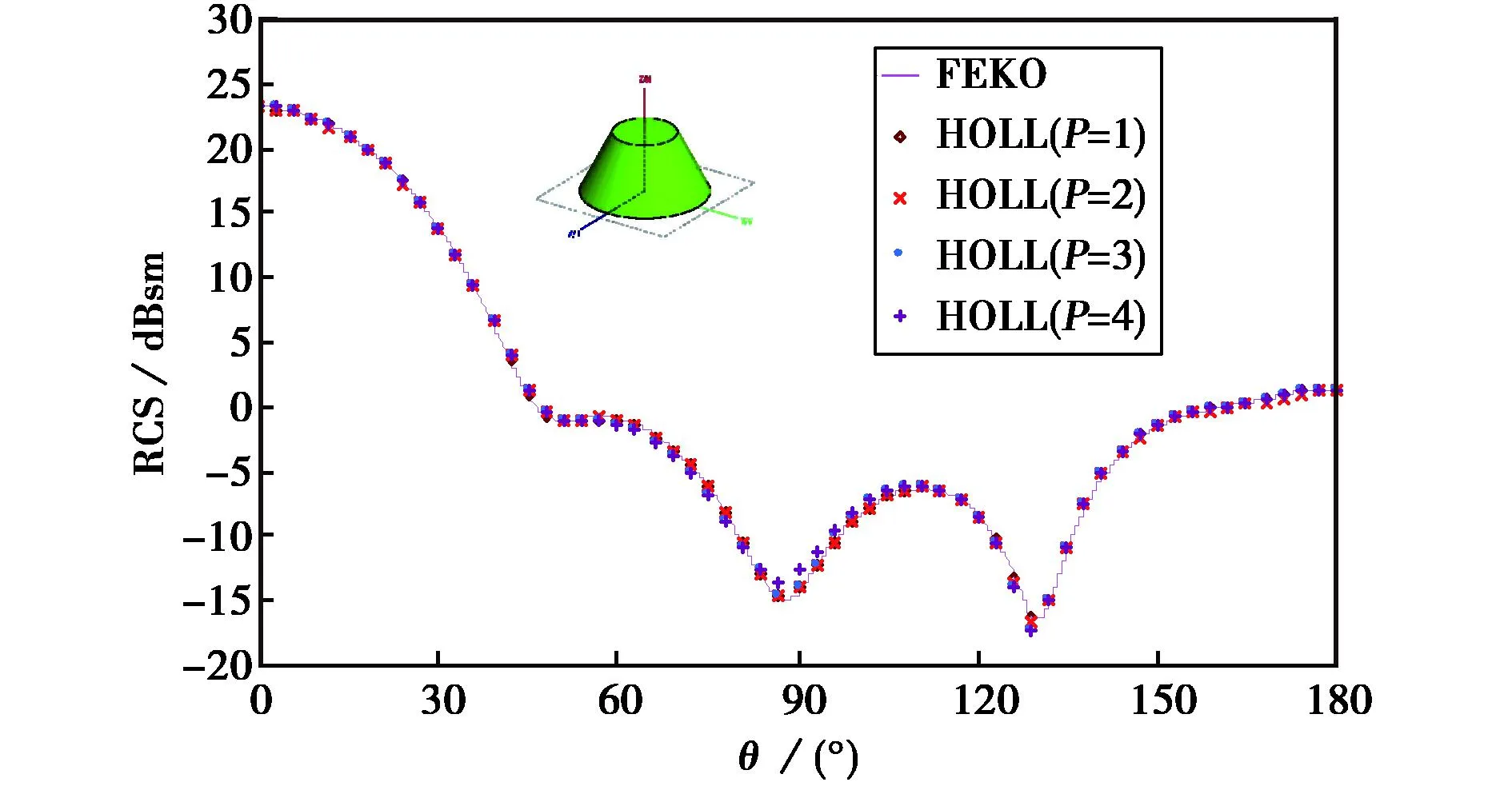
图3　算例2双站RCS计算结果对比

算例2是介质的圆台,圆台的上下底面半径分别为0.5m和1.0m,高1.0m,介质的相对介电常数为2.0,均匀平面波的入射角度为θi=0°, φi=0°,频率为300MHz,观察φ=0°平面随着θ角变化的双站RCS(VV极化). 在介质面上建立PMCHWT方程,将计算结果与FEKO○R矩量法的计算结果对比,如图3所示,可以看出,不同阶数的方程结果是吻合的. 表3给出了各个阶数下方程的剖分尺寸和未知量数,可以看出,基于双线性思想的高阶基函数在阶数高的时候可以采用大的剖分尺寸,减少未知量,依然满足积分方程精度.

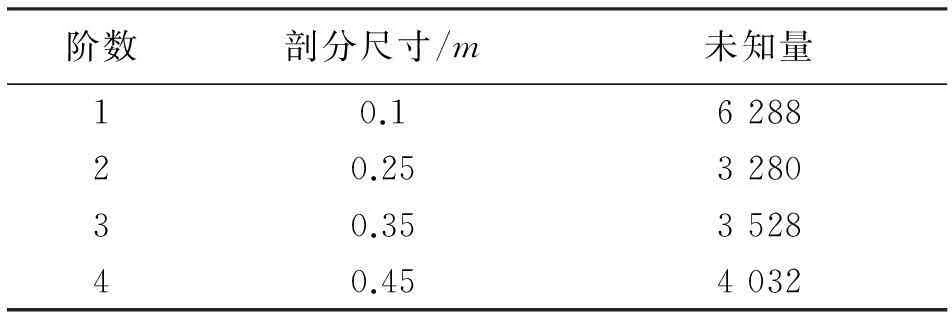
表3　算例2各阶数下方程计算时的剖分尺寸和未知量

4结论

本文提出了一种基于双线性思想的高阶基函数分析介质目标电磁散射问题,比较了不同阶数时所需未知量以及计算精度.数值算例表明该方法在高阶基函数时能节省未知量而依然满足积分方程的计算精度.

参考文献

[1]RAOSM,WILTONDR,GLISSONAW.Electro-magneticscatteringbysurfacesofarbitraryshape[J].IEEEtransactionsonantennasandpropagation, 1982, 30(3): 409-418.

[2]ZHALP,HUYQ,SUT.EfficientsurfaceintegralequationusinghierarchicalvectorbasesforcomplexEMscatteringproblems[J].IEEEtransactionsonantennasandpropagation, 2012, 60(2): 952-957.

[3]GRAGLIARD,PETERSONAF,ANDRIULLIFP.Curl-conforminghierarchicalvectorbasesfortrianglesandtetrahedral[J].IEEEtransactionsonantennasandpropagation, 2011, 59(3): 950-959.

[4]任仪, 聂在平, 赵延文. 基于高阶叠层矢量基函数的加速迭代求解方法[J]. 电波科学学报, 2008, 23(1): 100-105.

RENY,NIEZP,ZHAOYW.AnaccelerationiterativesolutionofMoMmatrixequationbasedonhigherorderhierarchicalbasisfunctions[J].Chinesejournalofradioscience, 2008, 23(1): 100-105. (inChinese)

[5]TRINTINALIALC,LINGH.Firstordertriangularbasisfunctionsforelectromagneticscatteringanalysis[J].Journalofelectromagneticwavesandapplications, 2001, 15(11): 1521-1537.

[6]ERGÜLÖ,GÜRELL.Linear-linearbasisfunctionsforMLFMAsolutionsofmagnetic-fieldandcombined-fieldintegralequations[J].IEEEtransactionsonantennasandpropagation, 2007, 55(4): 1103-1110.

[7]JINJM.Thefiniteelementmethodinelectromagnetics[M]. 3rded.NewJersy:JohnWiley&Sons,Inc., 2014.

[8] 《数学手册》编写组. 数学手册[M]. 北京: 人民教育出版社, 1977: 582-590.

[9]GRAGLIARD,WILTONDR,PETERSONAF.Higherorderinterpolatoryvectorbasesforcomputationalelectromagnetics[J].IEEEtransactionsonantennasandpropagation, 1997, 45(3): 329-342.

[10]李晓峰, 谢拥军, 王元源, 等. 半空间电大均匀介质目标散射分析方法[J]. 电波科学学报, 2009, 24(3): 518-522.

LIXF,XIEYJ,WANGYY,etal.Scatteringfromhomogeneousmediumwithelectricallylargesizeinhalfspace[J].Chinesejournalofradioscience, 2009, 24(3): 518-522. (inChinese)

[11]王海龙, 吴群, 吴健, 等. 一种高效的计算Mie级数的新方法[J]. 电波科学学报, 2006, 21 (6): 811-815.

WANGHL,WUQ,WUJ,etal.AnewandhighlyeffectiveapproachforcalculatingtheMieseries[J].Chinesejournalofradioscience, 2006, 21(6): 811-815. (inChinese)

樊振宏 (1978-),男,江苏人,南京理工大学电子工程与光电技术学院副教授， 博士生导师，主要研究方向为计算电磁学及天线分析与设计.

何姿(1988-),女,河北人,南京理工大学电子工程与光电技术学院博士研究生,研究方向为计算电磁学、电磁散射与目标特性等.

陈如山(1965-),男,江苏人,南京理工大学电子工程与光电技术学院教授，博士生导师，研究领域包括微波毫米波集成电路与系统、电磁脉冲与瞬态电磁场、雷达与电磁兼容技术、计算电磁学.

作者简介

中图分类号O441

文献标志码A

文章编号1005-0388(2016)01-0106-05

收稿日期：2015-04-03

樊振宏, 何姿, 陈如山. 介质散射的双线性高阶叠层基函数矩量法分析[J]. 电波科学学报,2016,31(1):106-109+128. DOI: 10.13443/j.cjors.2015040301

FAN Z H, HE Z, CHEN R S. MoM analysis on the electromagnetic scattering of dielectric object by using high order bilinear basis function[J]. Chinese journal of radio science,2016,31(1):106-109+128. (in Chinese). DOI:10.13443/j.cjors.2015040301

资助项目: 国家自然科学基金(61431006，61371037)； 南京理工大学自主科研专项计划(30920140121004)

联系人： 樊振宏 E-mail: zhfan@njust.edu.cn