基于藤Copula-POT的多资产尾部相依结构的研究

田文晓，梁冯珍(天津大学 理学院，天津市 300072)



基于藤Copula-POT的多资产尾部相依结构的研究

田文晓，梁冯珍(天津大学 理学院，天津市 300072)

摘要：在基于pair-Copula高维建模方法的藤Copula理论框架下，构建了藤结构Copula-POT模型，并采用C藤和D藤结构分解下的Gaussian Copula和Frank Copula函数来研究外汇资产间的尾部相依结构.该模型考虑了单个资产的尾部特征，且克服了传统Copula的“维数灾难”问题，能更好地描述资产尾部间的相依结构.基于四种外汇资产(美元、欧元、日元和港币)的实证结果表明D藤能更好的对外汇资产间尾部相依结构进行描述，且D藤分解模式下的Frank Copula能更准确反映外汇资产尾部间的相依性，并针对外汇储备投资，给出相应的建议.

关键词：藤Copula；外汇投资；POT理论；尾部相依结构

我国国际储备资产构成中，绝大部分为外汇储备.如何进行外汇储备投资以缓解汇率风险十分重要.风险管理通常不关注投资组合损益的整体分布情况，而是分布的尾部，即市场极端情况下的损益，因而研究外汇资产间尾部的相依结构十分必要.

大多数金融市场之间都存在着较强的非线性相关关系，即相依性.作为研究相依性的主要方法之一，基于Copula理论的相依性分析法受到国内外许多学者的青睐.尽管标准的Copula函数能够较好地刻画多个金融资产之间的相依性[1]，但在更高维情形下的刻画效果却不很理想，而藤Copula方法弥补了这一不足.

藤Copula是Bedford等[2]在简单构造模块pair-Copula的基础上引入的一种构造复杂多元相关结构模型的新方法，它将多元联合密度函数分解成一系列pair-Copula模块和边缘密度函数的乘积，为二元Copula方法推广到高维情况提供了理论基础.在藤Copula中应用最广泛的是C藤Copula和D藤Copula.C藤Copula方法于2009年由Heinen等[3]引入到金融领域中，并获得了很好的应用.

目前，国内应用藤Copula方法来研究外汇资产间尾部特征的文献还比较少[4].考虑到金融资产分布表现出“尖峰后尾”特征，本文把极值理论[5]引入到单个资产损益分布的估计中.并尝试借用藤Copula理论框架，通过构建藤Copula-POT模型来研究我国外汇资产间尾部相依结构，这为了解外汇储备投资与进行外汇资产风险管理提供了一定的参考依据.

1模型介绍

1.1藤Copula方法介绍

考虑n维随机向量X=(X1,…,Xn)，其联合分布函数为F(x1,…,xn)，根据Sklar定理可知，多元分布函数可以通过Copula函数和随机变量的边缘分布函数Fi(i=1,2,…,n)表示为：

F(x1,…,xn)=C(F1(x1),…,Fn(xn))

给定连续的联合分布函数F(x1,…,xn)和边缘分布函数Fi(i=1,2,…n)，则多元联合密度函数为：

f(x1,…,xn)=c12…n(F1(x1),…,Fn(xn))·f1(x1)…fn(xn)

其中:c12…n(·)表示n维Copula密度函数，fi(xi)表示边缘密度函数.

同时，n维联合密度函数也满足：

f(x1,…,xn)=fn(xn)·fn-1(xn-1|xn)……f1(x1|x2,…,xn)

由此可得其条件联合概率密度函数：

f(x|v)=cxvj|v-j(F(x|v-j),F(vj|v-j))·f(x|v-j)

此处，vj表示n维向量v中任意一个分量，v-j表示向量v去掉vj后得到的向量.

藤结构Copula是在Copula的基础上发展而来，能够更好地描述高维资产间的复杂相关性.

对于高维的联合分布，藤结构Copula的分解不惟一.Bedford和Cooke[2]引入一种称为规则藤的图形分解工具来描述藤结构Copula的逻辑分解结构.藤由树、边和节点构成，每棵树上的节点代表一个藤结构Copula的密度函数.根据Berg，藤较传统的多维Copula模型有更大的优越性，其中D藤和C藤最常用最简单的两种藤结构.一般而言，当变量集中出现引导其他变量的关键变量时，适合用C藤构建多变量联合分布结构，而当变量集中变量间关系相对独立时，可以用D藤来描述.为简单起见，本文只描绘C藤和D藤四元分解结构图.如图1所示，多元分解结构按此进行扩展.根据两种藤结构各自的结构特点对n维联合密度函数进行分解可得：

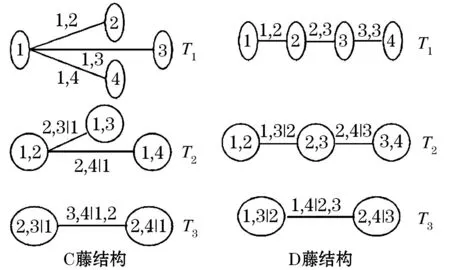
图1　C藤与D藤的四元分解结构图

D藤分解下的概率密度函数可表示为：

f(x1,…,xn)

C藤分解下的概率密度函数可表示为：

f(x1,…,xn)

这里，j表示藤结构中的第j棵树，i表示每棵树中的第i个结点，n表示维数，f(xk)表示边际分布的密度函数，Cxvj|uj(·，·)表示每棵树上的藤结构Copula的密度函数，它由两个条件分布函数F(x|v)组成，Joe[6]的研究表明：

F(x|v)=∂Cxvj|vj(F(x|v-j),F(vj|v-j))//(vj|v-j)

其中，Cxvj|v-j表示二元Copula分布函数.藤结构Copula中采用的二元Copula函数主要有：GaussianCopula、ClaytonCopula、GumbelCopula、frankCopula和t-Copula.其中，t-Copula有自由度和相关系数两个参数，其他则都只有一个参数.考虑到ClaytonCopula只能描述二元分布的下尾相关性，GumbelCopula只能描述二元分布的上尾相关性，而frank-Copula能描述二元分布的上尾与下尾相关性，故本文选用GaussianCopula和frankCopula来进行研究.

1.2极值理论POT模型Copula

金融时间序列往往是尖峰厚尾并且非对称的，而极值理论[5]专注研究分布的尾部特征，能够比较准确的拟合尾部真实分布，对尾部风险进行有效控制.为充分利用数据的有效信息，本文使用POT模型来拟合人民币汇率损益分布的尾部.POT模型主要基于广义帕累托(Pareto)分布(GPD)：

这里，ξ为形状参数，β>0为尺度参数.根据Pickands[7]：对于一个充分大的阈值μ, 超出量(x-μ)的分布收敛于Gji(x).据超出量分布函数的定义得：

其中：x>μ，F(x)为随机变量的累积分布函数，Fμ(x-μ)为超过阈值μ的分布函数.则：

F(x)=(1-F(μ))Fu(x-μ)+F(μ)

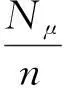
2实证分析

2.1数据分析

本文选取2005年7月25日～2014年1月14日的美元、欧元、日元、港币兑人民币汇率中间价作样本数据，每种汇率共2062个数据，得2061个日负对数回报.数据来源于中国国家外汇管理局网站.日负对数回报Rt定义为：

-Rt=100*(lnPt-lnPt-1)

其中：Pi为t时刻的人民币汇率中间价，日对数回报乘以100是为了更好地观察其统计特征.数据描述性统计结果如表1，显然，四种汇率数据序列都是尖峰厚尾的，因为其偏度不为0且峰度大于3.而且两种汇率的JB统计量远大于0，表明它们均

不服从正态分布.

表1　四种外汇资产日对数收益率的描述性统计

2.2藤结构Copula-POT模型的参数估计

藤结构Copula-POT模型的参数包括边际分布的参数和各个Copula的参数.当随机变量的个数为n时，二元Copula的数目可达n(n-1)/2，模型的待估参数数目可以达到n2数量级.因此，当n较大时，采用普通的极大似然估计方法会涉及到高维优化问题，使问题变得十分复杂.本文采用Patton[8]等人提出的两阶段极大似然估计法，即先对边际分布的参数进行极大似然估计，然后再估计由Copula刻画的相关结构的参数.该方法不仅计算简单，且计算精度不亚于普通极大似然估计法.

2.2.1POT边缘分布参数估计及拟合检

应用极值POT模型来拟合实际数据的分布时，首先需要根据样本数据序列确定合适的阈值.通常情况下，阈值的选择需要多方权衡才能确定.若选择的阈值偏小，则在用广义Pareto分布估计超出量分布时会产生较大偏差.若偏大，则较少的超额数据会增加估计误差.本文综合使用MEF图和Hill图来确定阈值.图2～5分别给出了四个序列的MEF图和Hill图.经分析，最终确定的阈值由表2给出.四序列分别得到120、114、105和109个超出量数据作为极值数据，分别占原始数据的5.8%、5.5%、5.0%和5.2%.据McNeil和Frey[9]的结论：“在阈值允许的情况下，选取2%～6%左右的数据作为极值数据组是比较合适的，否则可能会出现样本内过度拟合，样本外不适用的情况”知，本文对阈值的值的选取是较合适的.

图2　USD/RMB汇率序列的样本MEF图(A)和Hill图(B)

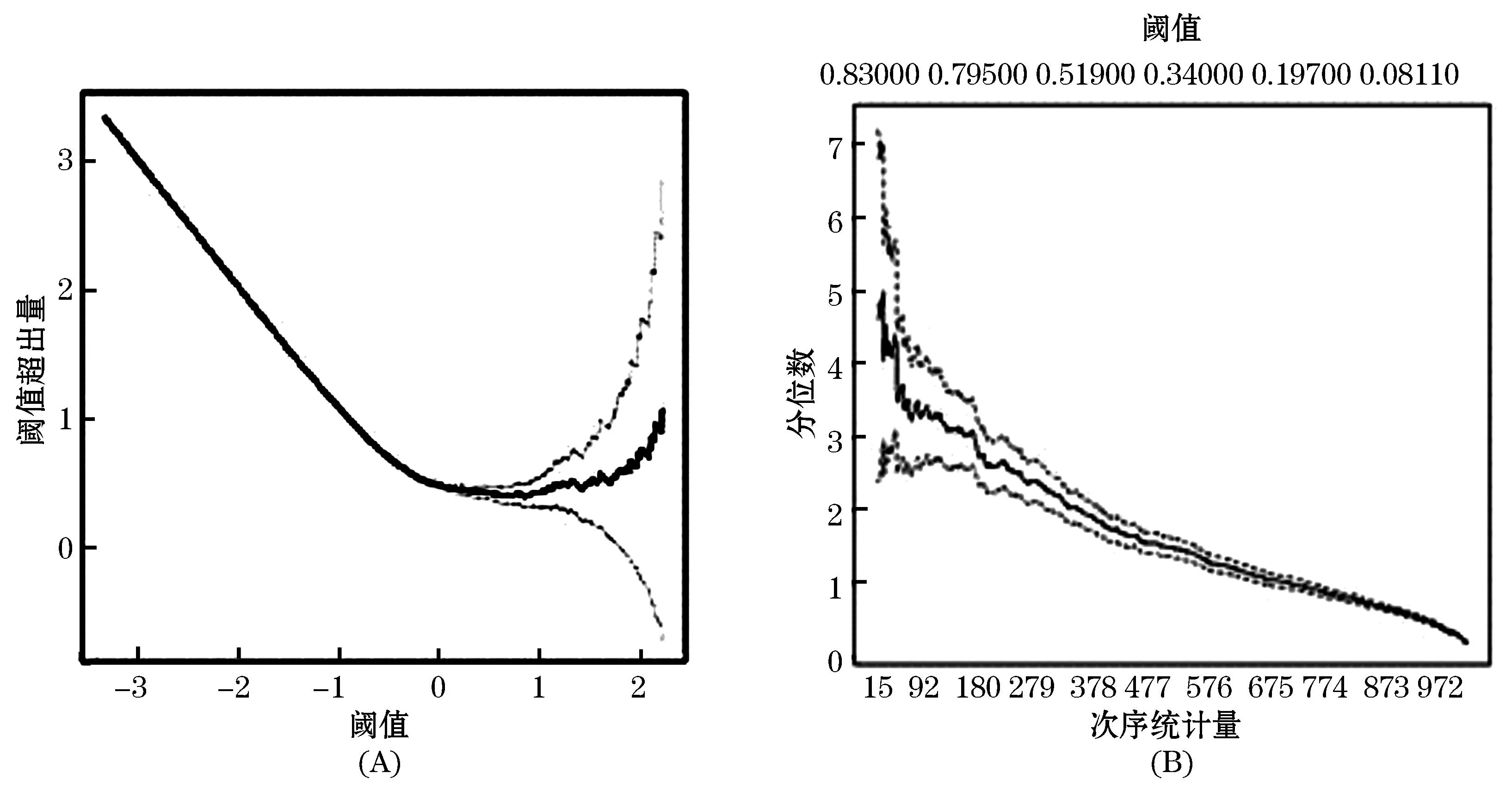
图3　EUR/RMB汇率序列的样本MEF图(A)和Hill图(B)

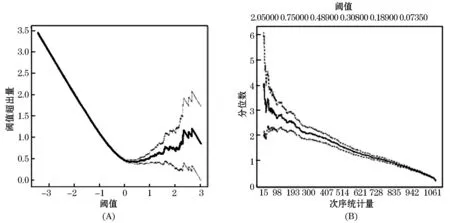
图4　JPY/RMB汇率序列的样本MEF图(A)和Hill图(B)

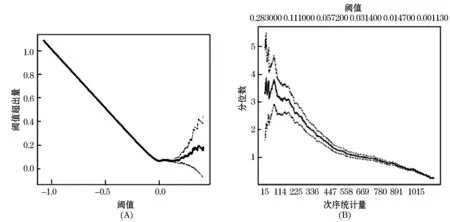
图5　HKD/RMB汇率序列的样本MEF图(A)和Hill图(B)

2.2.2藤Copula函数的参数估计及结果分析

Hosking等证明在ξ≥-1时，参数β，ξ基于极大似然(MLE)法的估计比其他估计方法更加有效.因此本文在基于超出量数据进行GPD分布拟合时，采用MLE法估计分布参数β，ξ，结果如表2.图6(A)～(D)分别给出四个序列的超出量分布拟合图.结合图6与K-S检验结果(如表3)可知，POT模型能很好地拟合两序列的边缘分布，也再次说明本文对的取值是合适的.

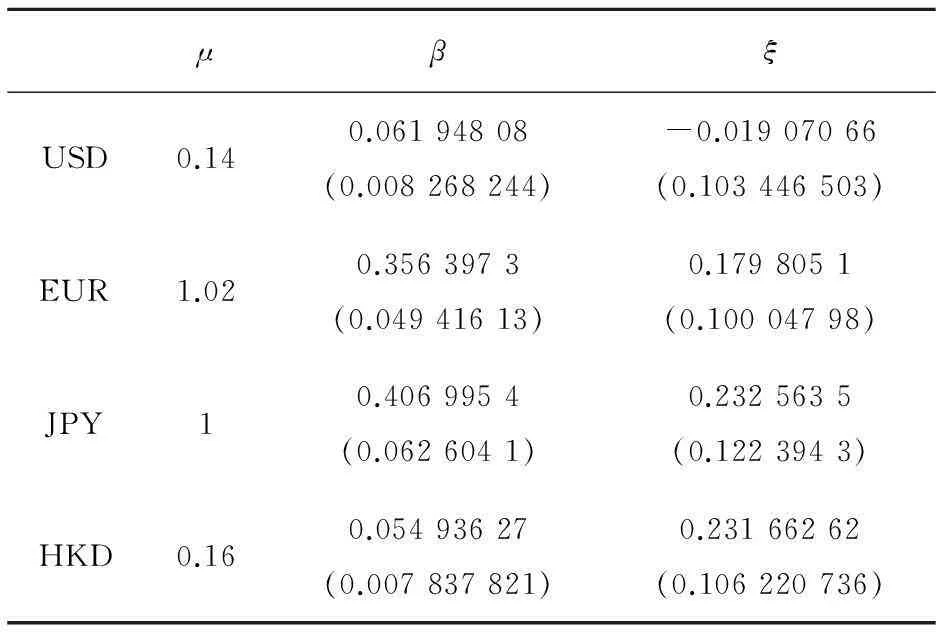
表2　边缘分布拟合参数值

表3　边缘分布拟合效果K-S检验

在估计出各边际分布的参数后，采用极大似然估计法估计藤结构Copula模型的参数值，可通过R软件CDVine包相关命令实现.表4(A)、(B)分布给出了C藤、D藤Copula模型的参数估计结果.据表4可知，由于二者分解模式不一样，因此两者的估计结果也存在一定的差异.至于D藤和C藤哪种结构能更好地描述汇率序列尾部相依结构，本文将采用AIC和BIC准则予以判定.AIC值和BIC值越小，则说明效果越好.下面给出二者的定义：

AIC=-2L+2K，BIC=-2L+2K×logT

其中：L表示对数极大似然函数值，K表示待估参数的个数，T表示样本容量.

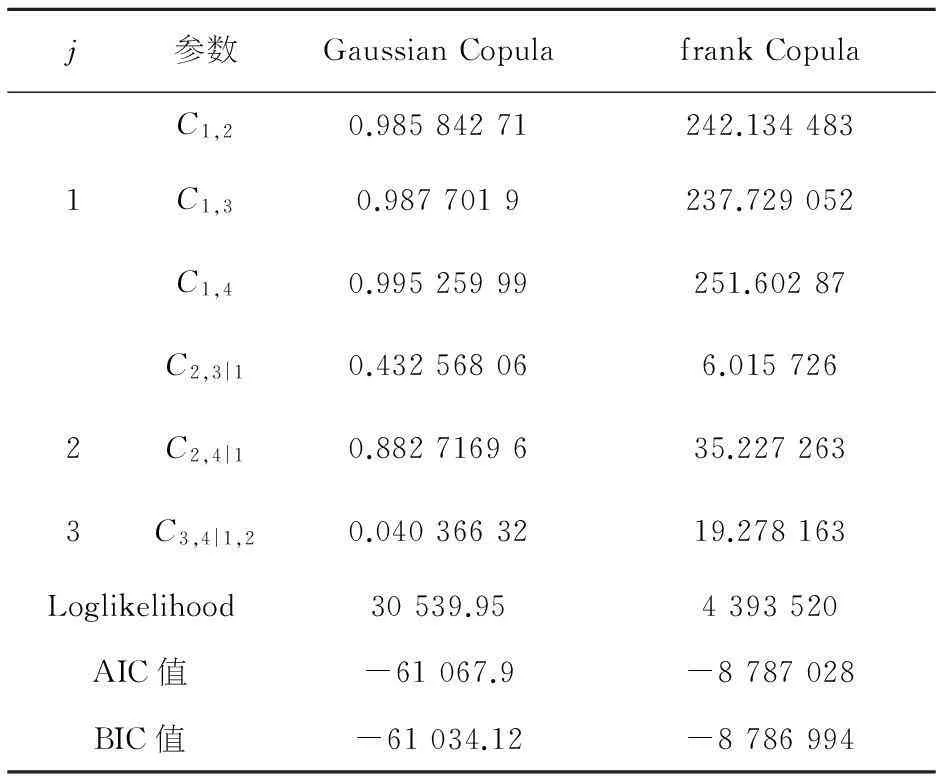
表4(A)　C藤Copula模型参数估计值、

由表4可知，相对而言，D藤的分解模式更适合描述本文的数据.这主要是由我国外汇储备结构的变动引起的.我们知道，美元是国际支付、结算和投资的主要货币，美元价格变化对其他货币价格的变化都有重大影响.但是由于近年来，我国外汇储备采取多样化战略，央行在减少美元在外汇储备中配置的同时，也增加购买日元等传统资产.故用C藤Copula模型刻画各外汇资产尾部间的相关结构并没有体现出其优势.另一方面虽然我国增加了其他外汇资产的配置，但这部分的比例仍然较低，因此D藤Copula所表现出的优势也并不是很明显.

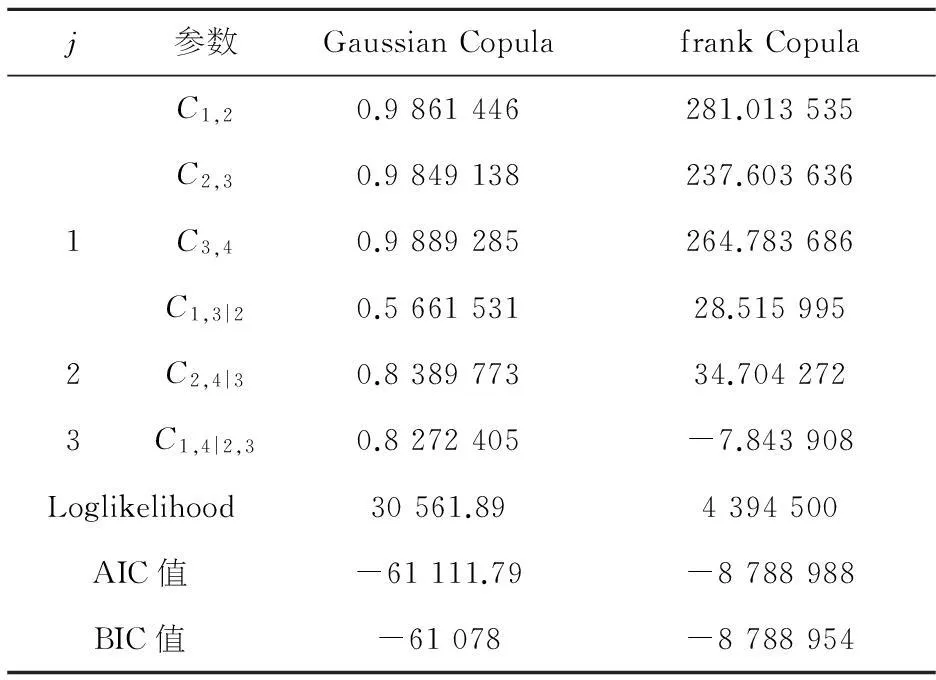
表4(B)　D藤Copula模型参数估计值、对数似然

另外，我们发现与Gaussian Copula相比，frank Copula能更好描述外汇资产尾部间的相依结构.这是由于Gaussian Copula描绘的是线性相关性，而金融资产之间的相关性往往比较复杂.

对于四种外汇资产而言，两两之间的尾部相关性相近，且均为正相关，但在条件变量的作用下，却表现出较大差异，甚至出现负相关情况.这告诉我们，在进行外汇储备投资时，不要单一地集中在某种资产或某两种资产上，而应该增加外汇资产的多样性，以尽可能规避风险.同时，由于黄金市场活跃度高且流动性大，又不存在信用风险，使其能够对冲尾部风险，因此我们也可以引入黄金实现储备多样化.

图6　四汇率序列的超量分布拟合图

3结语

本文在藤Copula理论框架下，结合极值理论，通过构建藤Copula-POT模型，并采用C藤和D藤结构分解下的Gaussian Copula和frank Copula函数来研究四种外汇资产之间的尾部相依性结构.得出的主要结论有：1)C藤和D藤分解模式刻画的资产间尾部相依性结构存在一定的差异；2)在描述外汇资产的极值数据特征时，D藤分解模式下的frank Copula模型效果较优.

藤Copula-POT模型不仅能很好地克服现有时间序列统计模型对高维资产特征描述不充分问题，且能较好地刻画单个资产的尾部特征与高维资产间的相依结构.如何构建既能考虑资产组合维数的影响，又能捕捉到组合内部各资产相关结构的差异性，将是作者之后要研究的方向.

参考文献：

[1]张超锋, 张莉敏, 李乔. 基于 Pair-Copula 构造的多元相依结构模型分析[J]. 统计与决策, 2014(19): 24-27.

[2]BEDFORD T, COOKE R M. Probability density decomposition for conditionally dependent random variables modeled by vine [J]. Annals of Mathematics and Artificial Intelligence, 2001, 32: 245-268.

[3]HEINEN A, VALDESOGO A. Asymmetric CAPM dependence for large dimensions: The canonical vine autoregressive model [R]. New York: SSRN, 2009: 1297506.

[4]马超群, 金凤, 杨问昱, 等. 基于藤结构Copula-SV模型的外汇投资组合风险分析[J]. 统计与决策, 2013(6): 152-156.

[5]史道济. 实用极值统计方法[M]. 天津: 天津科学技术出版社, 2006.

[6]JOE H. Family of m-variate distributions with given margins and m(m-1)/2 bivariate dependence parameters [J]. Lecture Notes-Monograph Series, 1996, 28: 120-141.

[7]PICKANDS J. Statistical Inference Using Extreme Order Statistics [J]. Annals of Statistics, 1975, 3(1): 119-131.

[8]PATTON A J. Estimation of Multivariate Models for Times Series of Possibly Different lengths [J]. Journal of Applied Econometrics, 2006, 21: 147-173.

[9]MCNEIL A J, FREY R. Estimation of Tail-Related Risk Measures for Heteroscedastic Financial Time Series: An Extreme Value Approach [J]. Journal of Empirical Finance, 2000, 7(3): 271-300.

Study on tail dependence structure among foreign exchange assets based on vine Copula-POT model

TIAN Wen-xiao, LIANG Feng-zhen

(School of Science, Tianjin University, Tianjin 300072, China)

Abstract：Under the vine Copula theory framework based on high dimension modeling method of pair-Copulas, the vine Copula-POT model was built. Gaussian and frank Copulas based on Canonical vine(C-vine) and D-vine structure decomposition methods were used to study the tail dependence structure among foreign exchange assets. The model not only considered the tail characteristics of the individual asset, but also overcome the “dimension disaster” caused by traditional Copulas. The empirical results based on foreign exchange assets showed that the tail dependence structure could be described more accurately by D-vine, especially by the frank Copula based on D-vine structure decomposition method. At last, some suggestions are presented for the foreign exchange investment.

Key words：vine-Copula; foreign exchange investment; POT; tail dependence structure

中图分类号：F224

文献标识码：A

文章编号：1672-0946(2016)01-0084-07

作者简介：田文晓(1988-)，女，硕士，研究方向：极值统计.

收稿日期：2014-12-23.