多因素GM（1,N）模型在城市道路交通噪声预测

孙红影(三亚学院,海南　三亚　572000　)



多因素GM（1,N）模型在城市道路交通噪声预测

孙红影
(三亚学院,海南三亚572000)

摘 要：城市道路交通噪声是影响人民生活质量的一项重要因素，本文采用Newton-Cores公式优化后的GM(1.N)模型，对南方某城市道路交通噪声进行预测。

关键词：交通噪声；GM(1,N)模型；背景值优化

0　引 言

随着经济的发展，人民的生活质量提高，城市交通噪声已经开始影响我们的生活。特别是北京，上海以及南方发达城市，问题更加的严重，城市道路交通污染系统包括诸多因素，如人口数量，道路长度，车辆数量[1-2]。

本人以文献[3]中南方某城市道路交通噪声数据为例，利用多因素考虑的GM（1，N）模型对道路交通噪声进行预测，并与实际数据进行比较，说明多因素的GM（1，N）预测精度更高。

1　灰色GM（1，N）预测模型背景值原理

GM（1，N）模型背景值的求法实际上就是数值分析中的梯形公式，然而在实际计算应用中，梯形公式的误差较大，致使GM（1，N）模型的模拟值误差较大。在区间对公式(3)的两边进行积分

整理后得到

2　基于Newton-Cores公式的GM（1，N）模型优化

公式写作

Newton-Cores积分系数一般取n£4，基于稳定性和精度考虑，现取n=4。则有

3　仿真实例分析

为了便于比较，本文采用文献[2]中所给的数据。文献[2]给出了2002～2009年南方某城市道路交通噪声平均声级检测数据，以及对该城市道路交通噪声影响程度最大的两个相关因素数据，即道路行车线长度及常住人口，如表1所示。

表1　南方某城市道路交通平均噪声、道路行车线长度及常住人口数据表

因原始数据较大，在此我们利用灰色关联分析中的初值化算子对表1内的基础数据进行初值化处理，实现了数据的无量纲化，结果见表2所示。

表2

将未经优化的原始 GM（1，N）模型记为模型1，基于Newton-Cores公式优化的 GM（1，N）模型记为模型2，将文献[2]中的数据带入上述两个个模型同时进行建模，所得模型数据如表3所示。

从表3中可以看出，文献[2]的GM(1,N)模型预测 值的平均误差为5.4415%，而经过本文优化的GM(1,N)模型所得预测值的平均误差分别为4.6813%，其预测精度远高于原GM(1,1)模型。通过实例验证可知模型具有较好的精度。

4　结论

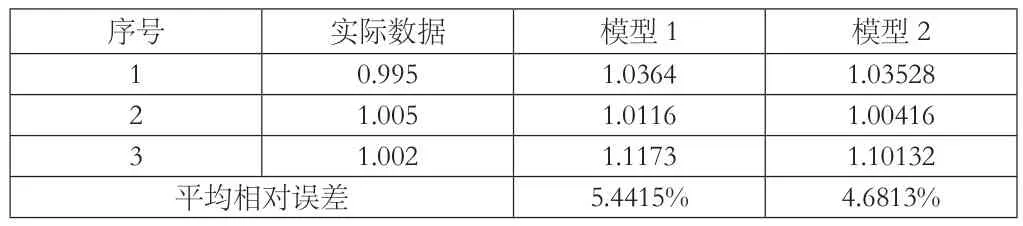
表3　南方某城市2006～2009年的交通预测值

根据仿真实验证明，利用多因素GM(1,N)模型预测城市道路交通噪声，模型精度高，预测结果可靠。

本人研究证明，利用灰色系统研究城市道路交通噪声是可行的，为今后对城市规划以及噪音处理提供了有力可行的科学方法。

参考文献:

[1]张超,陆愈实,章博等.GM(1,N) 模型在城市道路交通噪声预测中的精度分析[J].中国安全生产科学技术,2005,01(02):67-70.

[2]王素萍,温莉霞.灰色系统GM(1,N)模型在城市环境噪声预测中的应用[J].噪声与振动控制,1999,19(01):40-43.

[3]H . Li, X. C. Peng, Z. Q. Zhong, etc. “Influence Factors and Control Countermeasures of Traffic Noise Based on Grey Relational Analysis,”Noise and Vibration Control. Shanghai, vol.22, pp. 93-95,February 2012.

作者简介：孙红影（1983-），女，黑龙江人，硕士,助教，教师，研究方向：不确定性系统与信息处理。

DOI :10.16640/j.cnki.37-1222/t.2016.01.232