黑箱系统多目标参数优化的研究与应用
赵虎 成卢强 侯晓音 徐明


任何一项工程或一个产品的设计,都需要根据设计要求,合理选择方案,确定各种参数,以期望达到最佳的设计目标。本文建立了广义参数优化方法用以解决黑箱系统的参数优化问题,该方法以试验设计为基础,进行实验方案选择;采用人工神经网络建立因素与目标的非线性映射关系模型;利用遗传算法,获得给定参数区间的Pareto最优解集。提出的方法具有通用性,可广泛应用于各种基于试验或虚拟试验的黑箱系统多目标参数优化问题的求解。
一、确定实验方案
在有目的的进行试验、获得试验样本数据中,一般可采用全面试验方法、正交试验设计方法和均匀设计方法。
全面试验方法是在确定试验样本中,将每一个因素的不同水平组合做同样数目的试验。如在试验中,当因素为s=4个,每个因素有q=12水平,采用全面试验方法则至少需作qs=124=20736次试验。
正交设计方法利用一种规格化的表格正交表安排试验,使之只做较少次数的试验就可判断出较优的条件。其特点是:每个因素的各个不同水平在试验中都出现相同的次数;任何两个因素的各种不同水平的搭配,在试验中都出现了,并且出现的次数相同。即“均匀搭配”、“整齐可比”。用正交试验安排试验,则至少要作q2个试验。当q 较大时,q2将变得很大。例如,对于上述同样问题, q2 =122=144,这对多数实际问题,要求做的试验过多。因此正交设计方法只适用于水平数不多的试验中。
均匀设计方法是一种先进的试验设计方法,特别适合于多因素多水平的试验设计。均匀设计方法利用数论中的一致分布理论选取q个点,并且只需进行q次试验。对于上述同样问题,其试验次数仅为12。确定均匀设计试验点的关键是确定均匀设计表Um(qs),其中U表示均匀设计,m表示设计次数(布点数),q表示设计水平数,s表示设计因素。
在确定实验方案中,从节省时间和成本等方面考虑,一般都希望试验次数越少越好。但如果试验样本过少,会造成后续的建模误差较大,泛化能力下降,寻优精度降低。因此可根据实际问题的参数(因素)多少和其水平数综合进行考虑。在因素水平不变的情况下,当希望增加试验次数,可考虑选择正交设计方法或全面试验法;当希望减少试验次数,可考虑选择均匀设计方法。
二、建“黑箱”系统模型
本文提出的优化方法运用控制理论中的“黑箱”思想,把整个系统看成一个“黑箱”,按照实验设计方案安排试验 \ 虚拟试验,以此给出的设计参数作为系统的输入参数,试验结果数据作为输出参数。黑箱系统的具体实现采用人工神经BP网络模型。
BP(Back Propagation)模型是一种输入信号向前传播无反馈的多层神经网络,网络由一个输入层、一个或多个隐层和一个输出层组成。对于三层BP神经网络,其结构分别为:
(1)输入层节点i,其输出等于输入,xi(i=1,2,…,n)将控制变量值传输到第二层。(2) 隐层节点j,其输入hj,输出Oj 分别为
输入信号经过输入节点传向隐层各节点,经节点的作用函数作用后,传送至输出层节点,最后在输出节点上得到输出信号。如果输出节点的输出值与学习样本期望值之间存在误差,则误差反向传播,修正网络节点的连结权值。
由于人工神经网络的高度非线性映射能力,利用其网络的记忆功能形成了一个无明确表达式的虚拟函数,为下一步进行黑箱系统的优化打下了基础。
三、优化黑箱系统求解算法
多目标优化问题与单目标优化问题有着本质上的不同。多目标优化的解不是唯一的,而是存在一个最优解集合。解决多目标优化问题的最好方法就是得到均匀分布的Pareto最优解集后,根据不同设计要求和意愿,从中选择最满意的设计结果。
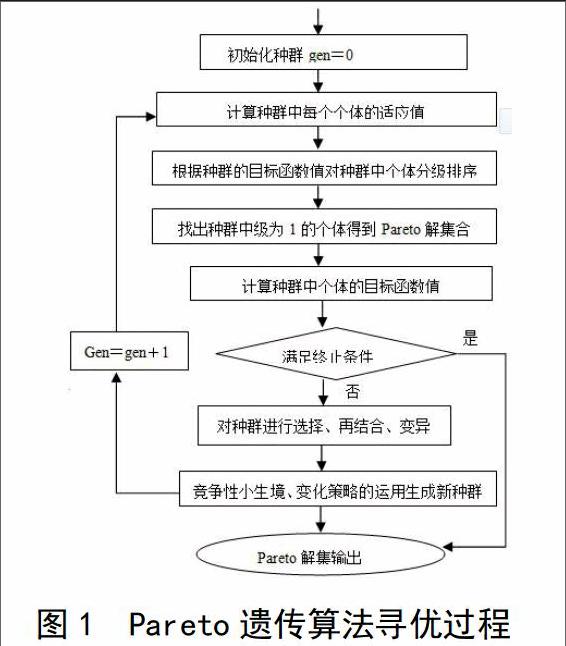
在本文的直接优化方法中,采用Pareto遗传算法作为其优化求解器,Pareto遗传算法寻优过程如图1所示。
遗传进化算法首先按照设定的初始种群数目在设计变量取值范围内用实数编码的方式进行随机编码,生成初始种群,每个个体信息由待优化的设计参数组成。利用导入的神经网络模型对每一个个体求出目标函数值,根据个体的目标函数值对个体进行Pareto定级,找出级别为1 的一组个体得到Pareto解集,计算其目标函数值,满足要求为所求优化解。若不满足要求则对种群的个体进行选择、再结合、变异、移植等遗传算子操作,使用小生境方法生成新种群,再进行上述定级等操作生成新的一组Pareto解集,直到求出满足要求的Pareto解为止。
四、应用实例
由于工程应用的复杂性,获取理论目标值的难度非常大,作对比分析较困难。为了便于验证与分析,对FONSECA函数进行Pareto多目标寻优。该函数对两个目标函数的最小值共有三个Pareto解。这里假设不知道其优化模型,利用函数式来做试验,按照均匀设计方法安排试验方案,由此试验数据通过神经网络建立数学模型,由训练好的神经网络来计算遗传进化算法中适应值,并进行遗传算法寻优,最后通过对优化结果的检验来测试方法的有效性。
FONSECA函数可描述为:
目标个数为2个,因素个数为2个,选择均匀设计表U20(202)安排试验,该表表示有两个因素(设计变量),每个因素取20个水平,共进行20次试验。其试验结果如表1所示。
在获得试验数据后,接下来用试验样本点训练神经网络,建立黑箱模型。当BP网络隐层神经元数选为7时,训练循环次数为100,网络误差为1e-3,满足要求。训练好的网络可以求出约束变量范围内任何一组设计变量对应的目标值。
训练样本目标值为Train,训练样本网络拟合值为Out1。当隐层神经元数为7个,输出层神经元数为1个,隐层和输出层的传递函数都定为logsig函数时,网络的误差最小。测试样本目标值为函数计算的精确值,Out2为测试样本的网络拟合目标值。BP网络参数与误差的关系如表2所示。
在完成上述建模工作基础上,采用遗传进化算法进行寻优,程序的输出结果是最优目标值:〔0.849767,0.824728〕,最优个体是〔-0.1366,-0.4209〕。
遗传算法求出的Pareto解与理论解之间的误差为:
五、结论
本文提出了广义参数优化方法将试验设计方法、人工神经网络技术及Pareto GA算法结合在一起,利用神经网络的高度非线性映射能力、遗传算法的全局搜索能力、试验设计方法在试验范围内均匀散布等特点,可在试验区内寻找出最优解或近似最优解。
该方法的应用范围广泛,不要求建立具体的优化数学模型,可解决无法构建数学模型的黑箱系统参数优化问题。

