阶梯圆盘轴向辐射声压的分布

李家星， 贺西平， 刘豆豆

(陕西师范大学 物理学与信息技术学院, 陕西省超声学重点实验室， 陕西 西安 710119)



阶梯圆盘轴向辐射声压的分布

李家星， 贺西平*， 刘豆豆

(陕西师范大学 物理学与信息技术学院, 陕西省超声学重点实验室， 陕西 西安 710119)

摘要：利用叠加法和高斯数值积分算法，以二阶梯圆盘为例推导了多阶梯圆盘轴向声压的分布，计算了轴向声压随距离的变化关系。对设计的二阶梯、三阶梯和四阶梯圆盘的轴向声压进行了测试，验证了理论计算的正确性。进一步得到了轴向辐射声压与输入电功率、圆盘的阶梯数目之间的关系。结果表明，阶梯圆盘轴向声压和输入有效电功率成正比；输入电功率一定时，轴向辐射声压与圆盘阶梯数目成正比。

关键词:轴向辐射声压；阶梯圆盘；输入电功率

PACS: 31.15.es

大功率超声在固体及流体介质中的应用日益广泛，如超声焊接、超声凝聚、超声清洗等[1-3], 相应地对超声振动系统的性能也提出了更高的要求。特别是在气体介质中，一般超声换能器辐射前端的特性阻抗远高于气体介质，这很大程度上制约了在气体介质中进行诸如超声悬浮、超声除泡等的应用[4-6]。在此类应用中如何与空气介质有良好的阻抗匹配是首先要解决的问题，而实现高指向性、大能量超声辐射又是对换能振动及辐射系统的另一要求。Gallego等人提出了与流体介质阻抗匹配较好的辐射体——阶梯圆盘[7-9]，利用纵振夹心换能器作为激振源，两者的组合可辐射大功率声波[10-11]。文献[12]提出了求解阶梯圆盘频率方程的数值计算方法，并对其辐射阻抗和指向性做了研究。文献[13]利用叠加原理推导了阶梯圆盘辐射阻抗的计算方法。文献[14]得出阶梯圆盘在给定激励频率下某一固定模态振动时的最大声辐射效率及圆盘在此状态时的尺寸。

当阶梯圆盘辐射面不在同一几何平面上时，之前的工作未对其轴向声压进行计算，本文从理论和实验两方面对阶梯圆盘轴向声压进行研究。将其按节圆半径分为中心平圆盘和外围圆环几个部分，以弯振平圆盘轴向声压的计算为基础，分别计算出各部分轴向声压，再依据叠加原理即可推导出其轴向声压的表达式。并利用高斯积分数值计算其结果得到了轴向声压与有效电功率和阶梯数目的关系。

1 阶梯圆盘轴向辐射声压的理论计算

1.1 弯振平圆盘轴向辐射声压

弯振圆盘是分布参数系统，振动面上的位移分布不均匀。计算声压时，可将弯振圆盘表面分成无限多个小面元，每个小面元均看作为一个点声源，在观察点P产生的声压为

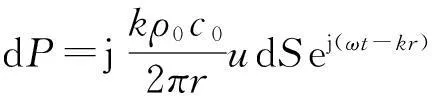
(1)

其中，dS为小面元的面积，r为小面元到观察点的距离，k为声波在介质中传播的波数，ρ0为传播介质的密度，c0为波速，u为平圆盘的振速。将所有这些点声源产生的声压叠加起来就可得到整个弯振平圆盘的轴向声压。

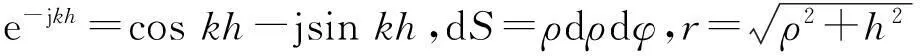
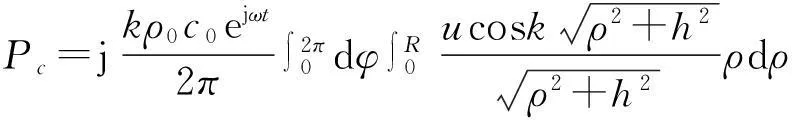
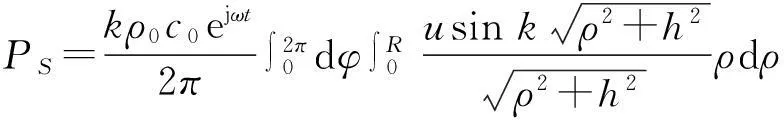
(2)

1.2阶梯圆盘轴向辐射声压

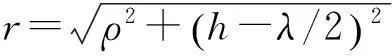
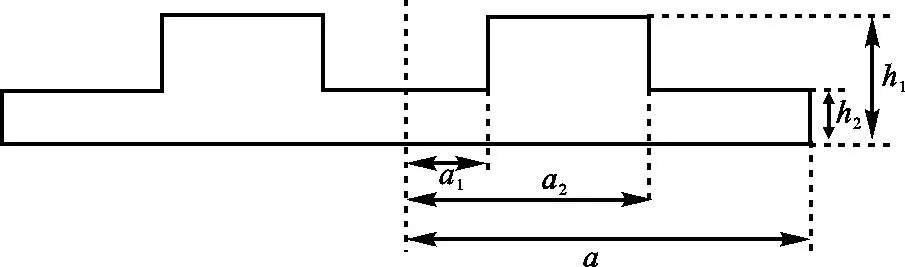
图1　二阶梯圆盘截面图

该盘的轴向辐射声压P可视作3部分贡献之和，即中间小平盘(其半径为a1，设其轴向辐射声压为P1)，中凸圆环(其宽度为a2-a1，设其轴向辐射声压为P2)及边缘圆环(其宽度为a-a2，设其轴向辐射声压为P3),公式为

P=P1+P2+P3。

(3)

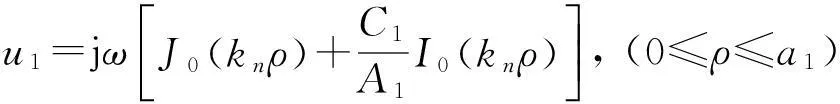
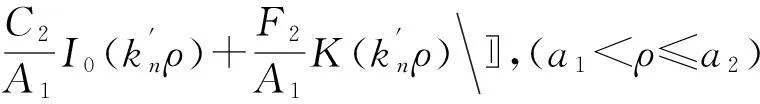
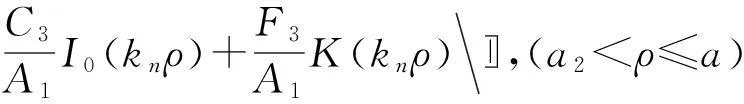
2轴向辐射声压算例

作为算例，取二阶梯圆盘基底厚度为5 mm，半径为5.75 cm，弯曲振动频率为20 kHz，盘的材料为钢，泊松比δ=0.28，材料密度ρ=7.8×103kg/m3，杨氏模量E=2.16×1011N/m2。利用公式(3)求解二阶梯圆盘轴向辐射声压时，被积函数的原函数不能用解析式表示，这里采用5节点的高斯数值积分，可得阶梯圆盘沿轴线的声压分布。为研究方便，本文将阶梯圆盘各点轴向声压与其最大轴向声压的比值定义为相对声压，求得二阶梯圆盘相对轴向声压与距离的关系，如图2中虚线所示。

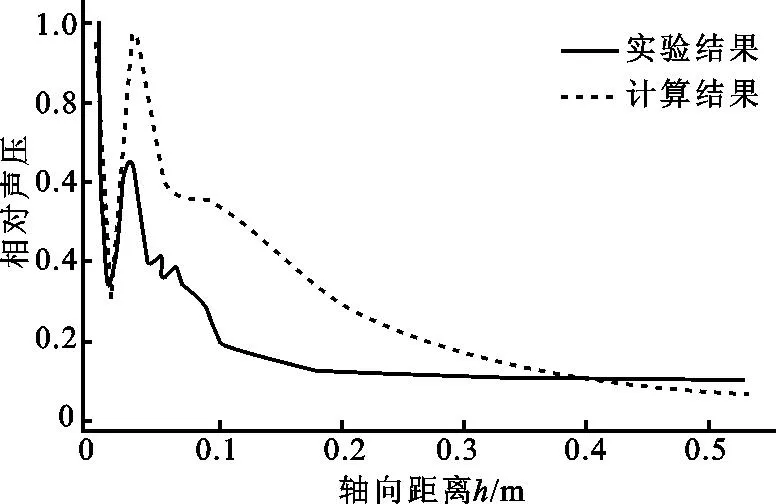
图2　自由边界二阶梯圆盘轴向辐射声压随h的变化

圆盘辐射声场分为近场和远场，声压最后一个极大值位置称为近远场临界距离。由图2知，此阶梯盘辐射声场的临界距离约为0.080 m;h<0.080 m时为阶梯盘轴向声场的近场区域，声压振幅随轴向距离增加有较大起伏;h>0.080 m时为阶梯盘轴向声场的远场区域，声压随距离的增加缓慢衰减。

3实验测试

测量了二阶梯圆盘轴向声压的声压级，由公式(4)将声压换算为声压级PSPL(dB)，验证了理论推导,研究了轴向声压与输入电功率及阶梯数目的关系。

(4)

式中pe为待测声压的有效值；pref为参考声压，在空气中取为2×10-5Pa。

3.1实验装置

由文献[17]可知，若测试环境的本底噪声声压级比测试声压声压级低ndB，则由本底噪声引起的测试误差(dB)为

(5)

测试阶梯圆盘轴向声压的实验在空旷的室外进行。测试环境的本底噪声约为65 dB，测量轴向声压的最小值为103.7 dB，由(5)式可知，本底噪声引起的测试误差为0.000 68 dB。测试仪器为日本理音公司的高精度传声器uc-29(口径为1/4英寸，测量频率为20 Hz~100 kHz，灵敏度为0.004 2 V/Pa)、前置放大器NH-5A(灵敏度为0.9 V/Pa)、转接头uc-12、传声器uc-29、精密噪声分析仪NA-42(测量频率为1 Hz~100 kHz)，Yikogawa公司生产的数字功率表WT1600(带宽为0.5 Hz~1 MHz，电流输入范围为10 mA~5 A，电压范围为1.5 V~10 000 V)，试验装置如图3所示。

图3　轴向声压测试装置

换能器、超声波发生器、数字功率表组成闭合回路。发生器产生连续正弦波，电功率表显示有效电功率、电压以及电流。传声器uc-29接收超声波，通过NH-5A前置放大器将声信号输入NA-42精密噪声分析仪。为避免阶梯圆盘前、后方的辐射声场相互影响，用大尺寸泡沫将盘的前后方隔开。确保传声器与阶梯圆盘的中心在同一高度，沿轴线方向前后移动传声器的位置就可测得电功率一定时阶梯圆盘轴向声压。

3.2轴向辐射声压的测试与分析

3.2.1沿轴向分布测量了算例中二阶梯圆盘轴向声压的声压级,换算为轴向声压，再用各点声压除以测量所得的最大值，即为各点的相对声压，如表1所示。相对轴向声压与轴向距离关系如图2中实线所示。

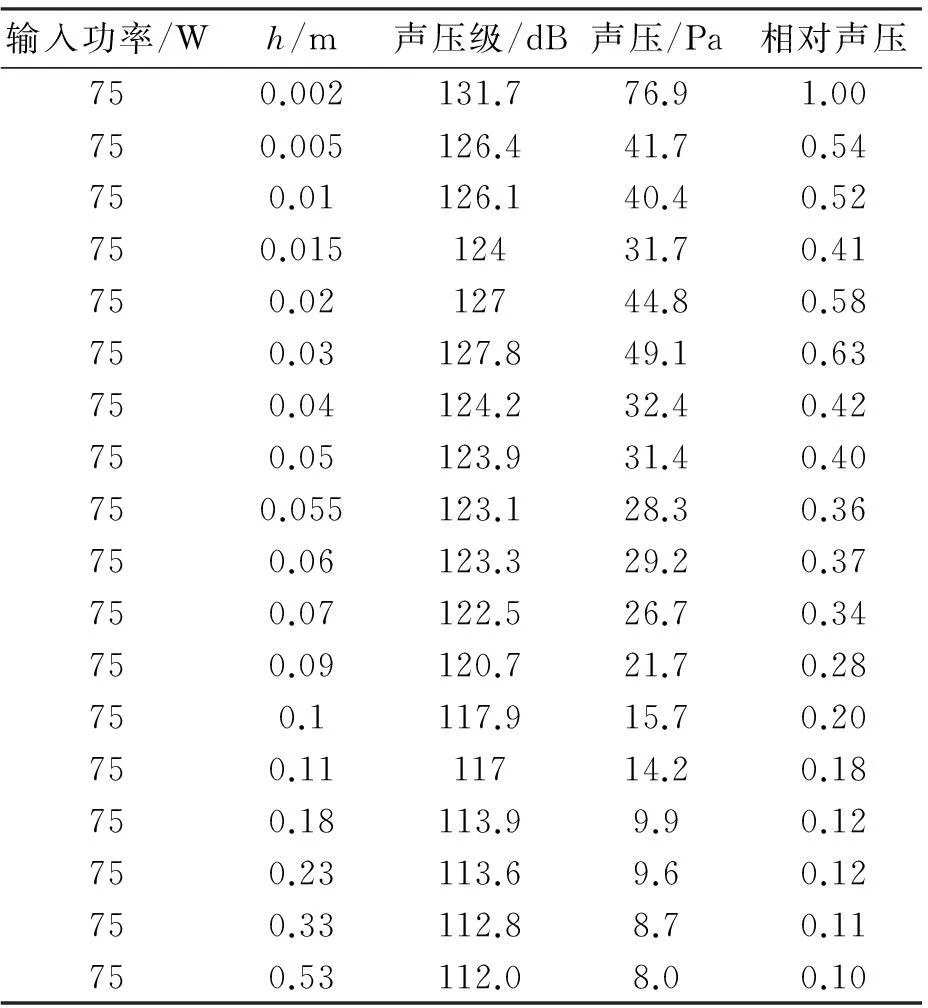
表1　二阶梯圆盘轴向声压

可以看出，输入电功率为75 W时，此二阶梯圆盘轴向声压的声压级最大值为131.7 dB。当h<0.060 m时声压振幅会上下起伏，为阶梯圆盘轴向声压近场区域;h>0.060 m时声压振幅随h的增大而减小，为阶梯圆盘轴向声压远场区域。阶梯盘的临界距离为0.060 m，图中显示该盘的临界距离的理论计算值为0.080 m，两者相差0.020 m。从0.060 m到0.011 m声压衰减了50%，从0.011 m到0.180 m声压衰减了31.6%，从0.180 m到0.530 m声压衰减了23%，可见在远场区域，随距离的增加声压减小程度越来越小。比较图2中虚、实线可知，计算与实验所得轴向声压随轴向距离变化的趋势一致。当h>0.030 m时轴向声压的计算值稍大于实验值。

3.2.2轴向辐射声压与电功率的关系 分别测量了二阶梯圆盘有效电功率为75、25 W时，三阶梯圆盘(基底厚度为6 mm、半径为7.37 cm、工作频率为31 kHz)有效电功率为15、40 W时轴向声压的声压级随距离的变化关系，如图4所示。

图4　不同功率下二、三阶阶梯圆盘梯轴向声压随h的变化

3.2.3轴向辐射声压与阶梯数目的关系对半径为5.75、11.1 cm(基底厚度为5 mm，工作频率为20 kHz)的二、四阶阶梯圆盘在输入电功率为75、25 W时轴向声压的声压级随距离的变化关系进行了测量,如图5所示。

图5　加载功率为25、75 W时二、四阶阶梯圆盘轴向声压随h的变化

4结论

本文在叠加法的基础上，以二阶梯盘为例，计算了声压沿轴线的分布，实验验证了计算结果，结论如下：

(1)在阶梯圆盘轴向声压的近场区域，声压分布不均匀，进入远场后，声压不断减小，且随距离的增加减小的程度弱化。

(2)输入电功率不同时，轴向声压随距离变化的趋势不变，电功率越大，轴向声压越大。

(3)加载相同电功率时，基底厚度、工作频率均相同的阶梯圆盘，阶梯数目越多(面积越大)，临界距离及轴向声压越大。

参考文献：

[1] CHRISTIAN H,ANIKA A.Ultrasonic welding of polyamide: influence of moisture on the process relevant material properties [J].Ultrasonics,2014,58(6):787-793.

[2] THOMAS L H.Environmental implication of acoustic aerosol agglomeration[J]. Ultrasonics,2000,38:353-357.

[3] CHANG Y, BAE J H, YI H C.Ultrasonic cleaning of used plastic parts for remanufacturing of multifunctional digital copier[J].International Journal of Precision Engineering and Manufacturing,2013,14(6):951-956.

[4] YAN N, GENG D L, HONG Z Y, et al.Ultrasonic levitation processing and rapid eutectic solidification of liquid Al-Gealloys[J].Journal of Alloys and Compounds,2014,607:258-263.

[5] 马希直，王挺，王胜光.近场超声悬浮启浮瞬态行为的理论分析及实验测试[J].声学学报，2014,39(1):93-98.

[6] GERMAN R,ENRIQUE R, GALLEGO-JUREZA J A.Experimental study of defoaming by air-bore power ultrasonic technology[J].Physics Procedia,2010,3:135-139.

[7] ALFONSO B, GALLEGO-JUAREZ J A. Flexural vibrating free-edge plates with stepped thickness for generating high directional ultrasonic radiation[J].The Journal of Acoustical society of America,1972,51(3B):953-959.

[8] GALLEGO JUAREZ J A, RODRIGUEZ-CORRAL G, RIERA-FRANCO de S E,et al.A macro sonic system for industrial processing[J], Ultrasonics,2000,38:331-336.

[9] GALLEGO-JUAREZ J A, RODRIGUEZ-CORRAL G, RIERA-FRANCO de S E, et al.Recent developments in vibrating-plate macro sonic transducers[J].Ultrasonics, 2002, 40: 889-893.

[10] GALLEGO JUAREZ J A, RODRIGUEZ G, ACOSTA V, et al.Power ultrasonic transducers with extensive radiator for industrial processing[J].Ultrasonics Sonochemistry,2010,17:953-964.

[11] CHACON D, RODRLGUEZ-CORRAL G, GAETE-GARRETON L, et al.A procedure for the efficient selection of piezoelectric ceramics constituting high-power ultrasonic transducers[J].Ultrasonics,2006,44:517-521.

[12] 贺西平,宋旭霞,李伟.阶梯圆盘的设计及其声参数计算[J].声学学报,2010,35(5):502-507.

[13] 贺西平.弯曲振动阶梯圆盘辐射阻抗的计算[J].物理学报,2010,59(5):3290-3293.

[14] 马奶连,贺西平.弯曲振动薄圆盘的最佳尺寸设计[J].云南大学学报(自然科学版),2014,36(3):366-370.

[15] 贺西平，张频，宋旭霞.单台阶同心圆盘辐射声场的指向性计算[J].声学技术,2009,28(5):673-677.

[16] 兰正康，贺西平，马焕培，等.阶梯圆盘阶圆偏离对辐射声场指向性的影响[J].振动与冲击,2013,32(12):105-109.

[17] 杜功焕，朱哲民，龚秀芬.声学基础[M].南京：南京大学出版社，2001:235.

〔责任编辑 李博〕

Study on the distributions of axial radiation pressure for stepped circular plates

LI Jiaxing, HE Xiping*, LIU Doudou

(School of Physics and Information Technology, Shaanxi Key Laboratory of Ultrasonic Shaanxi Normal University, Xi′an 710119, Shaanxi, China)

Abstract:The axial radiated sound pressure of stepped circular plates are investigated from both of theoretical calculations and experimental test. Taking a circular plate with two steps for example, the distribution of axial radiated sound pressure is derived using of superposition and Gaussian numerical integral method, and the variation of the axial sound pressure and distance are also calculated.The axial radiated sound pressure for the fabricated circular plates with two steps, three steps and four steps are tested in experimental and the results are according with theoretical calculations. Moreover, the relationship between the radiated sound pressure of input electric power and the number of steps of a circular plate are confirmed in experiment. It shows that the axial pressure increases with the input electric power.Furthermore when the input electric power is fixed, the axial pressure increases with the number of steps.

Keywords:axial radiated sound pressure; circular stepped plate; input power

中图分类号:O426.1

文献标志码:A

*通信作者：贺西平，男，教授，博士生导师。E-mail: hexiping@mail.china.com

基金项目：国家自然科学基金(11374201)

收稿日期：2015-05-08

doi:10.15983/j.cnki.jsnu.2016.02.225

文章编号：1672-4291(2016)02-0043-05

第一作者： 李家星，女，硕士研究生，研究方向为超声工程。E-mail:912741561@qq.com