基于博弈论在交通工程投标报价分析中的研究

黄　敏， 吴　立， 樊友川

(1.中国地质大学(武汉)， 湖北 武汉　430070；　2.湖北省交通运输厅造价管理站， 湖北 武汉　430034；　3.武汉经济开发区建设工程服务中心， 湖北 武汉　430056)



基于博弈论在交通工程投标报价分析中的研究

黄敏1，2， 吴立1， 樊友川3

(1.中国地质大学(武汉)， 湖北 武汉430070；2.湖北省交通运输厅造价管理站， 湖北 武汉430034；3.武汉经济开发区建设工程服务中心， 湖北 武汉430056)

[摘要]随着我国基础建设日益发展，博弈论在交通工程投标中得到广泛的应用。将对博弈论的原理、使用及其在招投标范围内的各种模型的构建展开系统的论述和研究，在深入理解并结合现有招投标现状的情况下构建出基于博弈理论总成本投标报价模型，从而为投标单位提供一些有针对性的报价模型及建议，帮助确定其投标报价，这样既能提高标单位的中标概率又可以使其获得最大期望收益，从而增强企业的竞争力。

[关键词]博弈论； 投标； 报价； 分析； 研究

0前言

当今社会竞争环境复杂，项工程目问题的结果需要多个行为主体共同确定。各行为主体既拥有各自的利益目标，又相互依存。招标单位采取的办法一般是复合标底，简单点说就是招标单位在投标前不确定自己的真实标底，而采用所有投标者的投标报价水平，通过加权取平均数确定最终的标底，这样就需要投标者主要凭个人经验来进行投标，因而带有很大的被动性。博弈论的理性决策需建立在各行为主体决策的预测结果之上，不可置他人决策于不顾而单独做出 。

1博弈论概述

博弈论是一个理性决策的过程，研究的主要问题是多个行为主体在风险不确定的情况下相互影响以及决策均衡性的问题；研究对象为具体的行为特征，在一定范畴内可以称之为对策论。

1.1博弈论三要素

① 局中人。

博弈活动的主要参与人、主导者，称之为局中人。在实际的应用中，局中人不但指自然人、集体，也可以指某种行为。用i来表示，i=(1，2，…，n)。在项目的决策中，局中人均以实现自身利益最大化为目标。

② 策略集。

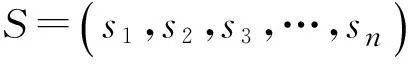
③ 支付函数。

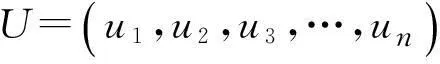
由于决策的制定由全局来确定，则Ui=ui(S)，表示第i个当事人在策略组合为S的情况下选择的支付函数为ui。

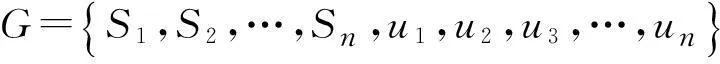
2招投标过程中的博弈分析

2.1招投标与博弈论的联系

招投标的过程，从理论上分析，也可以看出是一个博弈的过程。对应招投标的不同流程，参与的各个主体构成了博弈中的当事人，各主体之间的竞争关系，由各自的决策域不同直接表现。在最终决策的制定时，各主体又都受到他人决策结果的影响。这种影响体现在：开标之前，各个投标人对各自的投标价格并不知晓，而每个投标决策的制定又需要以他人决策的预测结果为前提。

经过分析可以看出，制定不同的投标人构成了博弈理论中的当事人，而各个投标人的决策制定构成了决策域，最终结果的制定共同构成了博弈理论中的支付函数。

在博弈论的体系中，通常情况下认为，当信息彼此知晓时，博弈的双方可通过简单谈判即可达成一种双方均能接受的协议。在当信息不完全公开情况下，则需分多个阶段多次交流才能保证所有参与人接受协议。若把招投标的具体过程进行仔细分析，可将采用不完全信息静态博弈模型为招投标模式。

2.2招投标过程中的常见博弈现象

2.2.1先开标后议标现象

项目开标后，针对工程价款、相关优惠政策的调整，通常情况下，招标人和投标单位会以议标的形式再次讨论。由于现今的建筑市场，施工单位不能给自己一个合理的定位，为了获取工程，总是以业主的意愿为基本前提，有时甚至不惜以竞相压价的形式以完成中标。一方面，这可以促使工程造价成本的降低，另一方面，却违背了公开招标的基本前提，与公开招标公平性相抵触。这也把社会生产的一般市场价值抛到脑后，有时就会造成施工企业无法按照既定目标完成工程，反而使得造价成本提高。

由以上分析可知，开标之后又议标实际上是对合同价确立的过度激励。对于目标的激励性，应有可观测性，也应对除投标标价之外的其他目标采取必要激励措施，保证目标的可观测性。若业主单位对招投标阶段的投资控制过度激励，很可能会造成施工单位盲目追求成本，忽视其他目标的现象。故业主应综合考虑各项因素，建立正确的激励机制。

2.2.2投标人联合

与投标人互相倾轧相反，有时为了获得正常的利润以外的超额利润，投标单位会联合起来对哄价进行抬标。这种现象称之为投标人联合。

站在博弈的角度分析，博弈的局中人指招投标主管部门和投标人，主管部门的策略为监督整个招投标过程中的是否违规现象，而投标人的策略为联合或不联合，两者共同构成支付函数。支付函数的最终确定，有超额利润来确定。投标人的联合，将对招标造成非常坏的影响，因此，招标单位应采取必要的措施来阻止这种现象的发生，也可以通过采用邀请招标的形式来实现，同时注意加强在投标截止日期前对所选的投标人的保密，使参与投标的单位彼此不知道有哪些单位参与竞标，建立起非合作型博弈，最终实现投标的有效性。

2.3招投标机制设置

招投标过程中的博弈分析，主要是指对评标方法的确定，而评标方法的确定主要是用来解决投标人的积极性。因此，所谓招投标机制的设置，主要是为了应用博弈理论对招投标活动进行约束。这种约束应从两个方面展开。

2.3.1个人理性的约束

在招投标机制的设置中，应充分考虑项目参与人的积极性，制定有效激励措施，促使项目参与人愿意在制定的机制中完成任务。最好的办法就是使得投标人获取标所得到的利润将远远大于失去这个项目的价值。可从如下几方面进行着手： ①注重于投标实际环境的分析，制定合理可行的标底。 ②在标底的计算中，要注意按照现有的工程量清单，按照市场价格求算标底。 ③对暂定标底权重的赋予，应将各有效投标报价中所占相同权重的报价进行加权平均，得到评分的基准价，实现对市场的正确引导。

2.3.2激励相容约束

本约束主要是为了尽可能的选出质量高、信誉好的企业。在激励相容约束的制定过程中，应注意使得所设计的机制尽可能的调动所有参与人的积极性，达到招标单位所期望的目标。激励制度的建立，要注意结合投标单位的实际情况，尽量避免过分激励和较弱激励的现象。

3博弈论在投标报价中的应用

3.1博弈论在“合成标底”评标中的应用

3.1.1合成标的打分法的介绍

现阶段最常见的评标方法就是合成标底打分法，也可称为复合标底法。该方法将标底进行量化，实现标底的可控制。基本步骤如下：

① 标底由招标单位制定，并给定一个浮动的百分比范围，当投标报价超过了所允许变动的范围时，视为废标。

② 对符合要求的投标单位的所有报价，包括招标单位的价格，进行加权平均，得到合成标底。

③ 以合成标底为依据，设定评分标准，对符合要求的投标报价进行综合进行打分。

3.1.2合成标的打分法的特点

具体说来共有3点： ①不可预知性； ②竞争性； ③合理性。所谓不可预知性是指标底的最后确定由几方共同确定，该次投标项目的标底通过加权平均的方法计算出来。竞争性是指评标方法在规则制定时对高于标底的报价制定严格的扣分机制最大程度的限制投标单位的投标报价。合理性是指最大程度上将标底的确定交给市场，并对不切实际的高报价和低保金完全不予考虑，使得复合标底比较合理，反映合理低价的标准。

3.2博弈论投标报价模型的构建

针对招投标过程的博弈展开研究，主要是为了防止 “围标”现象的出现。为了获得更加接近于真实情况的报价概率分布，模型的构建以评标中合成标底的做法为依托，以评标规则为依据，结合综合标底打分法完成。

3.2.1模型的假设

为了方便理解并简便该模型的计算步骤，本文对所构建模型做如下几个方面的假设：

① 在进行标底的编制中，将有些信息设为已知。且这种已知在现实的标底计算中，也是成立的，如定额编制办法中取费基数及取费费率的设定。

② 对评标方法、评标参数的确定在招标文件中进行设定说明，对某些变量进行固定。

③ 只考虑价格因素对投标报价的影响，其他的因素暂时忽略。

本文所构建的博弈论模型应以满足上述假设条件为前提进行，并此为基础前提进行研究。

3.2.2变量的设定

模型变量的设置如下：

Y：用以表示招标单位编制的招标标底，且本变量为一个相对数值，是可以发生变化的；

λ1：计算复合标底时，变量Y所占的权重；

λ2：计算复合标底时，所有投标人编制的投标报价所占的比重；

其中，(0<λ1、λ2<1，且λ1+λ2=1)

X：投标人制定的投标标价；

A：所有投标报价合格单位有效报价的加权平均数(同时规定，A值的取定，应在招标方制定的标底合理波动范围内)；

N：投标有效性的数量；

H：最终加权合成的标底；

L：招标方制定的扣分标准。

当投标方报价处于合成标底的有效范围内时得满分，超出范围或小于范围值时，相应的进行扣分。上文各变量的确定后，可以根据其逻辑关系得到下列几个计算式：

(1)

其中：xi是除了本方最终报价的其他竞争者的最终报价。

(2)

3.2.3报价模型

由公式(2)可知：对于标底H，我们可以得出我方对该项目报价与合成标底之间的差距，这个差距即是由于a和n在某种不确定性导致的我方报价与合成标底之间的误差E，则：

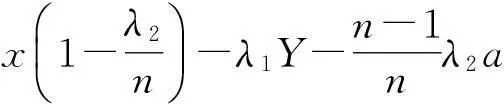
(3)

通过上式(误差计算式)可得扣分公式如下：

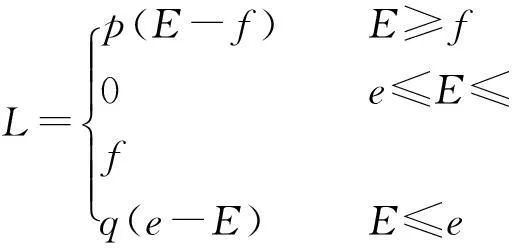
(4)

从理性投标人角度出发，本方投标的目的是为了保证报价中扣分尽可能的少，投标报价尽可能的大，最大可能的提升利润空间，即满足：

L→min，x→max。

这时需要注意的问题是，得分有一个限定的氛围，不以满分为标准设定，也就是说最终的中标者不一定获得满分，在运用本方法进行计算时，应将各个误差E用矩阵的形式来进行表示。如3.3所示，对于矩阵中的各数值由x和a两个因素决定。通过定性分析的方法，采用经验估计法确定报价平均值a的大致范围，以一定的百分比对各投标报价和我方报价在一定范围内按一定百分比进行依次取值，得出我方报价与合成标底的误差值，算出误差矩阵：

E= x-H=xl1∧xlnMMxm1∧xmnéëêêêêùûúúúú-hl1∧hlnMMhm1∧hmnéëêêêêùûúúúú=

e11∧e1nMMem1∧emnéëêêêêùûúúúú

(5)

结合上式，可得扣分矩阵如下：

L=l11∧l1nMMlm1∧lmnéëêêêêùûúúúú

(6)

其中，lij由计算式(4)计算得到。

最终，最优报价的确定，应以扣分矩阵的计算为基本前提，对所有的项目目标进行控制，实现L→min，x→max。

模型手工计算的前提是投标数量有限，当多家投标单位进行竞争时需要借助计算机辅助进行计算，防止出错。

4博弈模型实例计算

假定某投标公司准备投标，其中，令：

Y=1，λ1=0.6，λ2=0.4，

由此，可得标底：

同时，由于平均的投标价格及其有效投标人的数量n都是具有不确定的，这样投标公司的投标价格与合成标底就必然存在着不可控制的误差。当有了合成标底之后，就可以计算我方最终投标报价与合成标底的误差E了，其计算步骤如下：

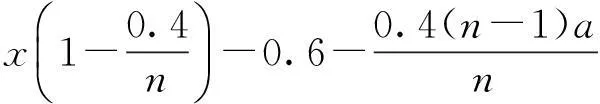
进而，组成报价误差矩阵模型，与以往类似项目投标相比较，其他各投标人报价均值a的范围可能在[0.96Y，1.00Y]范围，本次计算a在每隔0.5个百分点分别取一次值；我方报价x范围也暂定为[0.96Y，1.00Y]范围内，同时每隔0.1个百分点取值一次，将我方报价和报价均值分别代入误差矩阵中，得到以下博弈误差矩阵模型：

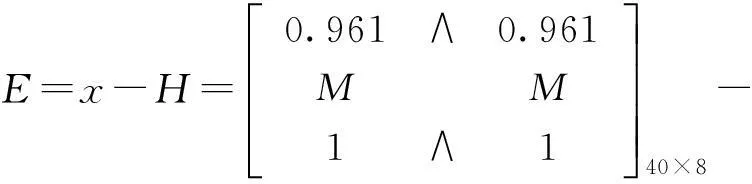
E=x-H=0.961∧0.961MM1∧1éëêêêêùûúúúú40×8-

0.6+an+(n-1)bn∧0.6+an+(n-1)0.4nMM0.6+0.4n+(n-1)bn∧0.6+0.4n+(n-1)0.4néëêêêêêêêùûúúúúúúú40×8=

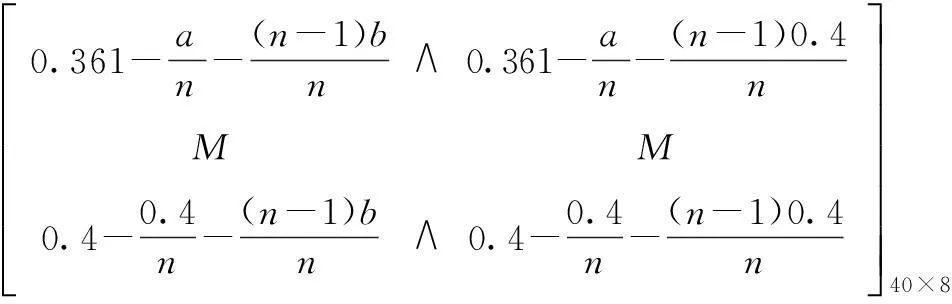
0.361-an-(n-1)bn∧0.361-an-(n-1)0.4nMM0.4-0.4n-(n-1)bn∧0.4-0.4n-(n-1)0.4néëêêêêêêêùûúúúúúúú40×8

式中：a=0.384 4，b=0.386。

L=l11∧l1nMMlm1∧lmnéëêêêêùûúúúú

在上述误差矩阵中将扣分原则代入可得本方的扣分矩阵L： 。

由上文中可以看出：理性人博弈的目的原则是L→min，x→max对上述博弈矩阵进行决策分析，开标开始前已知晓本次投标单位为六家，但是各个单位有效投标报价的数目并不确定。所以，将n=3，4，5，6分别带入到博弈模型的矩阵E中，分别得到各自的误差矩阵及扣分矩阵。

通过矩阵计算可知，对本方而言，我们得满分的报价区间见表1。

由上表可知：不论取值多少，只要n取值范围在(0.979 0Y，0.982 0Y)时，我方报价均可得满分。

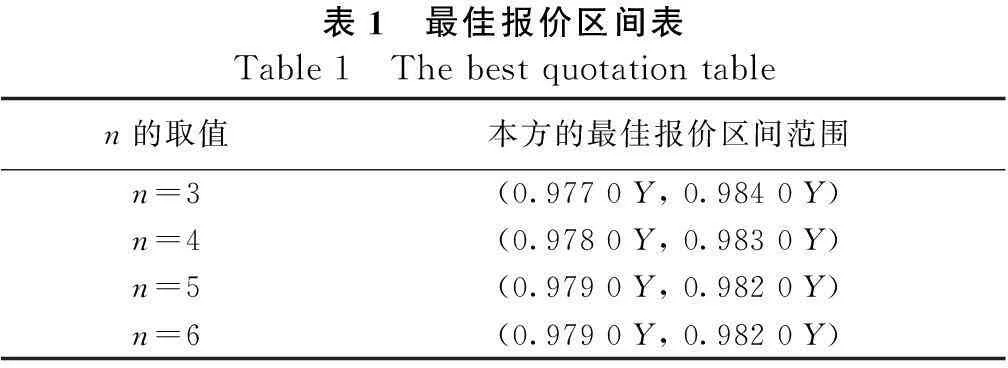
表1 最佳报价区间表Table1 Thebestquotationtablen的取值本方的最佳报价区间范围n=3(0.9770Y,0.9840Y)n=4(0.9780Y,0.9830Y)n=5(0.9790Y,0.9820Y)n=6(0.9790Y,0.9820Y)

根据博弈中报价尽可能大的原则，我方报价取x=0.982 0Y。只要其他投标方报价在(0.95Y，1.00Y)范围内，我方就能获得满分。当然，这里并不排除其他投标方也和我方一样获得满分的可能。

5结语

本文着重对博弈理论展开研究和表述，系统的研究了博弈理论的发展、组织及对招投标实际问题的适用性。投标方以市场为依据，针对“合成标底打分法”的评标规则特点构建了基于博弈理论的投标报价模型，并通过实例进行简单验证，为今后的实际研究提供了理论支持。

[参考文献]

[1]马亚，刘振奎.博弈论在招投标中的应用[J].价值工程，2010(11).

[2]王成国，黄韬.现代经济博弈论[M].北京：经济科学出版社，1996.

[3]徐春华.复合标底投标报价博弈研究[J].价值工程，2009(1).

[4]江伟，黄文杰.博弈论在工程招投标中的应用分析[J].工业技术经济，2004(1).

[5]方德海.合理低价中标方式下的投标策略博弈[J].工程经济，2003(8)：29-30.

[6]许高峰.国际招投标[M].北京：人民交通出版社，2001.

[7]张明媚.工程招投标中的激励机制分析[J].数学的实践与认识，2002(3).

[8]施锡铨.博弈论[M].上海：上海财经大学出版社，2000.

Analysis of Game Theory in the Traffic Engineering Bid Quotation

HUANG Min1，2， WU Li1， FAN Youchuan3

(1.China University of Geosciences， Wahan， Hubei 430070， China；2.Traffic Construction Cost Management Station of Hubei Province， Wuhan， Hubei 430030， China；3.Constrution Service Center of WEDZ， Wuhan， Hubei 430056， China)

[Abstract]With the development of China's infrastructure，game theory has been widely used in traffic engineering bidding.This paper will make a systematic study into the principle of game theory，its application and the construction of its various models in bidding.Based on the deep understanding of game theory and the present situation of bidding，a bidding model of the total cost will be built on game theory to provide targeted offer model and suggestions for the bidding units and help them to decide the tendering offer.In consequence，it can ensure the bidding unit of the successful bid probability or the largest expected profit，enhancing the competitiveness of enterprises.

[Key words]game theory； bidding； quotation； analysis； research

[中图分类号]F 224.32+1

[文献标识码]A

[文章编号]1674-0610(2016)01-0183-05

[作者简介]黄敏(1981-)，男，湖北阳新人，博士研究生，工程师，研究方向：造价管理。

[基金项目]湖北省交通运输厅科研项目(20137310303)

[收稿日期]2014-11-21