人行钢箱梁桥模态试验研究

申杨凡， 杨　斌， 何钰龙， 郭凯强， 续琦峰， 王艳琪， 贾艳敏

(东北林业大学 土木学院， 黑龙江 哈尔滨　150040)



人行钢箱梁桥模态试验研究

申杨凡， 杨斌， 何钰龙， 郭凯强， 续琦峰， 王艳琪， 贾艳敏*

(东北林业大学 土木学院， 黑龙江 哈尔滨150040)

[摘要]为了了解人行钢桥的自振特性，运用东华测试系统对某人行钢箱梁桥进行模态测试，得到桥梁的动力特性参数，并将试验测得的固有频率、模态振型与ANSYS有限元模型中的模态数据进行对比分析。分析结果表明：该人行钢箱梁桥的基频的试验值与理论值的误差为3.8%，行人的附加模态质量是对试验产生误差的原因之一，但对结构基频的影响不大，这也就证明了采用峰值拾取法处理时域数据是合理的，同时结合模态判定准则所得模态数据也是可信的，通过该模态测试系统可有效地测得模态参数(固有频率、模态振型及阻尼比)。

[关键词]人行钢箱梁桥； 模态测试； 有限元； 峰值拾取法

0前言

随着我国城市交通系统的不断完善，人行钢箱梁桥的数目日益增多，人行钢箱梁桥以其轻质高强、易于施工的特点被广泛应用于工程建设中[1]。国内诸多学者对人行钢箱梁桥进行了不同方面的研究，陈阶亮研究了各种行人荷载模式激励下绍兴路人行桥的振动响应，并对其试验桥梁进行了舒适度评价[2]；付一小研究了钢结构人行桥在桥梁下部通车作用下、人行荷载作用下、两者共同作用下的振动情况，并找出主要的影响因素和产生振动的原因[3]。以上研究都是以结构动力特性为基础加以深入研究的，因此，合理地测得人行钢桥的动力特性参数至关重要。

本文以某人行钢箱梁桥为工程依托，运用东华测试系统对该人行钢箱梁桥进行模态测试试验，采集人行钢箱梁桥的振动数据，并对所采集到的振动数据进行模态分析处理，得到各个测点的时域数据及经过快速傅里叶转换后所得到的频谱，利用峰值拾取法对数据进一步处理，得出人行钢箱梁桥的模态参数(固有频率、模态振型或阻尼比)，根据模态判定准则(MAC)直方图对试验结果进行校核，验证测试结果的正确性，并将试验测得的固有频率、模态振型与ANSYS有限元模型中的模态数据进行对比分析，所得结论可为该人行钢箱梁桥舒适性评价、结构损伤测试及相关规范地制定等作为参考依据。

1模态分析原理

模态分析是了解结构动力特性并以此分析结构动力响应的基础。其基本思想是将结构振动微分方程组中的物理坐标变换为模态坐标，解耦方程组，将其变换为一组以模态坐标及模态参数描述的独立方程，以此得出系统的动力参数。在结构的模态分析中，可将实际的结构看作一个多自由度的振动系统，考虑阻尼的多自由度运动微分方程如式(1)[4]

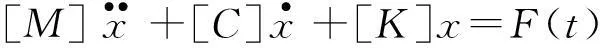
(1)

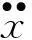
将多自由度结构的动力特性微分方程的两边进行拉氏变换(初始条件均为零)，并令s=σ+jτ，可得：

(2)

为拉氏变换因子；X(s)为位移响应拉氏变换；F(s)为激励力的拉氏变换。

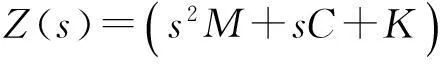
令 s =jω，便可得出在傅氏域中的阻抗矩阵及频响函数矩阵：

(3)

此时，得到系统的运动方程为：

(4)

由于H(ω)=Z(ω)-1，H(ω)矩阵中第i行第p列的元素可以表示为：

(5)

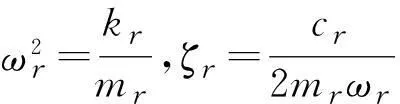
2试验研究

2.1工程概况

某人行天桥为三跨双悬臂连续钢箱梁桥，位于城市快速路及城市主干路的交叉口附近，是行人过街的唯一选择，该桥总长68.2 m，跨径14.8+34+17 m，箱梁高度为1.1 m，桥面宽3.3 m。主桥钢箱梁采用A3型号的钢板，桥面为大理石铺装。图1为人行钢桥立面图及主箱梁横断面图。

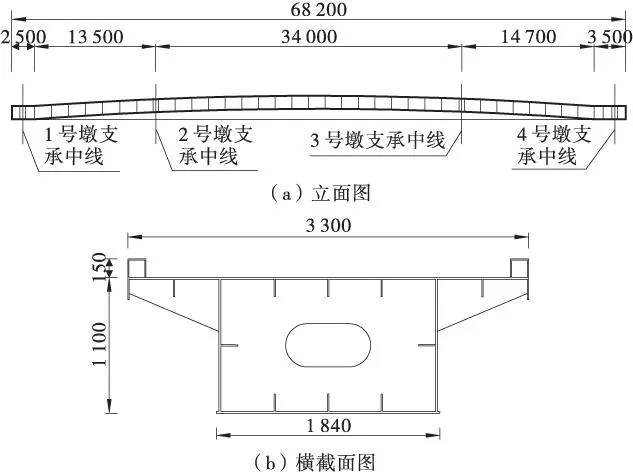
图1　人行钢箱梁桥主梁立面及横截面图(单位： mm)Figure 1　The elevation and cross-sectional view of the 　steel box girder footbridge(unit： mm)

2.2试验方案

本次试验采用江苏东华测试技术有限公司研发的东华桥梁模态测试系统，主要试验仪器包括传感器、路由器、笔记本电脑(DHDAS信号测试分析系统V4.3.58，DHMA模态分析软件2.6.3版)等，测点的布置为各跨的跨中、1/4跨及3/4跨位置处，参考点的位置设在不感兴趣模态的节点上，采用自然脉动激励的方法对该人行钢箱梁桥进行激振，采样频率为200 Hz，分析频率为78.13 Hz，采用连续采样的采样方式，试验过程中采用GSP同步卫星测试模式，增强各传感器之间的同步性，图2为试验桥梁测点布置图。

图2　试验桥梁测点布置图Figure 2　Measuring point arrangement of the test bridge

2.3试验数据处理及结果分析

对所采集的试验数据进行除去均值的处理后，采用快速傅里叶转换的方法对数据进行整合，得到各个测点的时域数据及经过快速傅里叶转换后所得到的频谱。采用峰值拾取法拾取相应的自互谱的共振峰，鉴于该方法具有一定的主观选择性，在使用该方法处理数据时注意相干密度须控制在0.7以上[5]，并在所得到的模态参数文件(自振频率、阻尼比)中利用模态判定准则(MAC)直方图对模态参数的正交性进行验证，图3为各跨跨中测点的时域数据，图4为各跨跨中测点在经过快速傅里叶转换后的频谱，图5为模态判定准则(MAC)直方图，图6为前三阶竖向振型图。

由试验结果可知：该人行钢箱梁桥的基频为3.91 Hz，符合《城市人行天桥与地道技术规范》(cjj69-95)中人行天桥上部结构的竖向自振频率不小于3 Hz的规定[6]。各跨跨中测点的频谱中相关函数在关键位置的分布较为明显，自互谱的共振峰也较为明显，个别无明显的共振峰可通过其他测点的共振峰找到。此外，该人行钢箱梁桥的阻尼比随阶数的增加而减小，一阶竖向频率与二阶竖向频率的差值较大，这是由于中间还存在有横弯的振动形式，因此，在较低的频率下，该人行钢箱梁桥的横弯及竖弯均为主要振动形式，前三阶竖向频率所对应的振型图的振动特征分别为对称竖弯、中跨倒S型竖弯及边跨竖弯、中跨S型竖弯及边跨竖弯。但由于测点布置得不够多，振型图的连续性尚未得到较好的体现，但已大体将振动的形式体现出来，在模态判定准则(MAC)直方图中也体现了该振动图具有较好的正交性，采用峰值拾取法对试验数据进行处理可有效的得出模态数据。

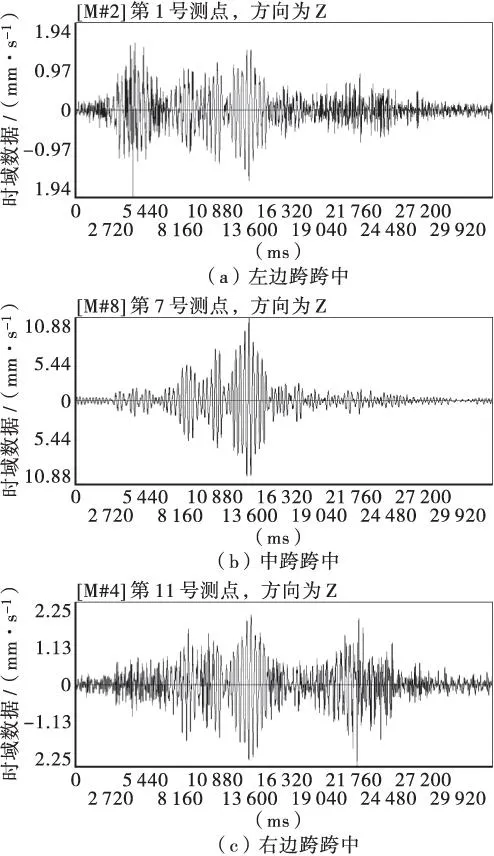
图3　各跨跨中测点的时域数据Figure 3　The time domain data of each measuring point 　on midspan

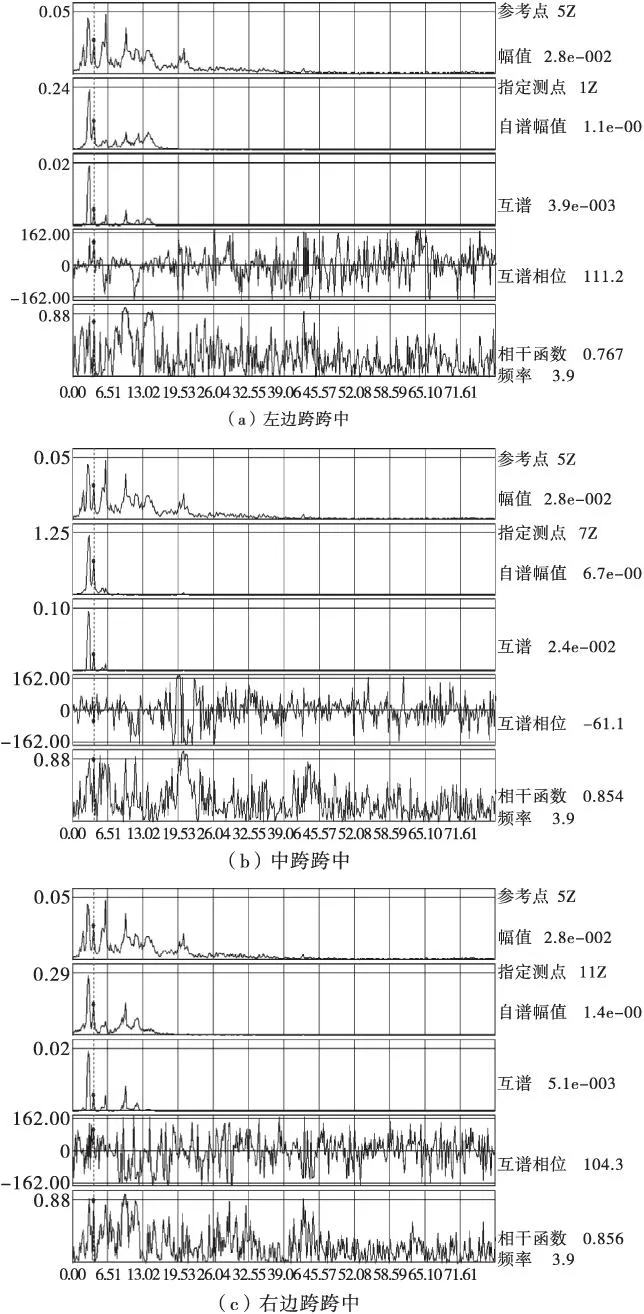
图4　各跨跨中测点在经过快速傅里叶转换后的频谱Figure 4　The frequency spectrum after a fast fourier transform 　of each measuring point on midspan

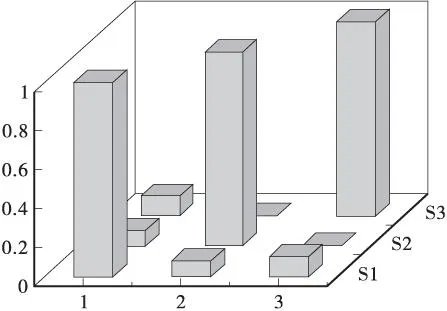
图5　模态判定准则(MAC)直方图Figure 5　The histogram of Modal criterion(MAC)

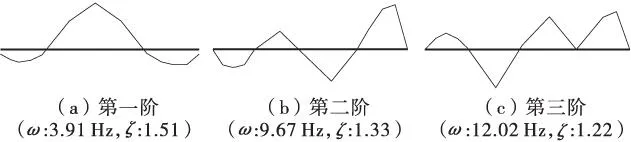
图6　前三阶竖向振型图Figure 6　The vertical vibration diagram of first three order

3有限元模型验证分析

对该人行钢箱梁桥建立ANSYS三维计算模型，模型采用材料库中的beam188梁单元，模型建立以后划分单元网格并施加约束，根据桥梁边界按照简支梁约束处理(约束类型采用节点约束)，对桥梁施加自重作用，并考虑该人行钢箱梁桥的二期恒载。图7为有限元计算模型。

图7　有限元计算模型图Figure 7　Finite element calculation model

采用Subspace法计算出人行钢箱梁桥前三阶竖向自振频率，表1为人行钢箱梁桥固有特性实测值与理论值对比表，图8为人行钢箱梁桥前三阶竖向频率所对应的振型图。

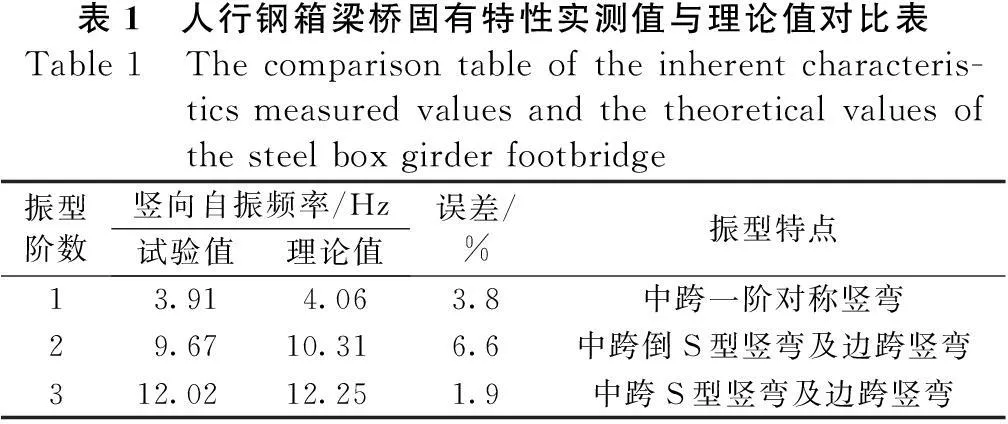
表1 人行钢箱梁桥固有特性实测值与理论值对比表Table1 Thecomparisontableoftheinherentcharacteris-ticsmeasuredvaluesandthetheoreticalvaluesofthesteelboxgirderfootbridge振型阶数竖向自振频率/Hz试验值理论值误差/%振型特点13.914.063.8中跨一阶对称竖弯29.6710.316.6中跨倒S型竖弯及边跨竖弯312.0212.251.9中跨S型竖弯及边跨竖弯

图8人行钢箱梁桥前三阶竖向频率所对应的振型图

Figure 8The vibration mode diagram correspond to the first three order vertical frequency of the steel box girder footbridge

由模态分析的结果可知，该人行钢箱梁桥的基频为4.06 Hz，符合《城市人行天桥与地道技术规范》(cjj69-95)中人行天桥上部结构的竖向自振频率不小于3 Hz的规定[6]。该人行钢箱梁桥的实测振型图与理论振型图的振型特点基本一致，而基频的试验值与理论值的误差仅为3.8%，足以保证本次试验的正确性。由于该人行钢箱梁桥在实际受力中，存在有人-桥竖向动力作用，行人会对该人行钢箱梁桥产生附加模态质量，而行人附加模态质量的贡献率为100%[7]，那么所测得的试验值自然就会比有限元值小，3.8%的误差也表明了行人所产生的附加模态质量对该人行钢箱梁桥基频的测试的影响不大。

4结论

通过模态测试试验所测得的试验结果与对ANSYS有限元模型进行模态分析后所得出的结果进行分析，所得结论如下：

① 模态判定准则(MAC)直方图有效的验证了模态数据的正交性，而实测振型图与理论振型图的振动特点也基本一致，竖向频率的试验值与有限元理论值也仅相差3.8%，充分验证了峰值拾取法是处理时域数据的有效方法之一，同时表明了运用此模态测试系统可有效的测得桥梁的模态要素(固有频率、模态振型及阻尼比)。此外，虽然试验所得出的振型图的连续性较差，但振型图的振动特点已得到了充分的体现。

② 该人行钢箱梁桥的阻尼比随阶数的增加而减小，对比竖向频率的试验值和理论值可知，试验测得的频率相比理论频率小，这是由于该人行钢箱梁桥还受到由行人所产生的附加模态质量的影响，3.8%的基频误差也表明了行人所产生的附加模态质量对该人行钢箱梁桥的基频的测试的影响程度不大。

③ 该人行钢箱梁桥的试验基频及理论基频均满足《城市人行天桥与地道技术规范》(cjj69-95)中人行天桥上部结构的竖向自振频率不小于3 Hz的规定[6]。

[参考文献]

[1]饶波.大跨度钢箱梁人行天桥设计[J].桥梁结构，2009，2(2)：30-32.

[2]陈阶亮.行人激励下人行天桥的振动舒适性研究[D].杭州：浙江大学，2007.

[3]付一小，叶见曙.道路交通引起城市人行钢桥振动特性分析[J].东南大学学报，2012，42(1)：144-149.

[4]傅志方.模态分析理论与应用[M].上海：上海交通大学出版社，2000.

[5]刘宗政，陈恳.基于环境激励的桥梁模态参数识别[J].振动测试与诊断，2010，30(3)：300-303.

[6](CJJ69)—95)，城市人行天桥与人行地道技术规范[S].

[7]李红利，陈政清.人-桥竖向动力相互作用效应理论与试验研究[J].土木工程学报，2014，47(6)：78-87.

[8]法永生，李东.某钢结构人行天桥动力特性测试与有限元分析[J].建筑结构，2007，37(3)：63-65.

[9]李峰，邹煜.基于环境激励的大跨度钢桥模态试验研究[J].机械，2012，39(2)：17-20.

[10]李爱群，丁幼亮.润扬大桥斜拉桥模态频率识别的环境变异性[J].东南大学学报，2007，37(2)：245-250.

[11]王洋，郝志军.ANSYS在土木工程应用实例[M].北京：中国水利水电出版社，2010.

Experimental Modal Anlysis of Pedestrian Steel Box Girder Bridge

SHEN Yangfan， YANG Bin， HE Yulong， GUO Kaiqiang， XU Qifeng， JIA Yanmin

(School of Civil Engi.， Northest Forestry Univ.， Harbin， Heilongjiang 150040， China)

[Abstract]In order to study the natural vibration characteristics of the pedestrian bridge steel，a pedestrian steel box girder bridge’s model experiment is carried out with Donghua Test System to get the dynamic characteristics of bridge，and comparing Natural frequency and mode shapes with modal data analysis of ANSYS finite element model.The analysis results indicate that the error between the fundamental frequency experiment value and the theoretical value of the pedestrian steel box girder bridge is 3.8%.And the additional modal mass of pedestrian is one of the reasons why the experiment have error，it’s influence is little.What proved that using the Peak Picking Method to manipulation time domain data is reasonable.At the same time，the modal date that obtained by combining with the modal criterion is credible.That modal parameters(natural frequency，modal vibration mode and damping ratio)can be measured effectively by the modal testing system.

[Key words]pedestrian steel box girder bridge； modal test； finite element； peak picking method

[中图分类号]U 448.21+3

[文献标识码]A

[文章编号]1674-0610(2016)01-0134-05

[作者简介]申杨凡(1993-)，男，湖南邵阳人，主要从事交通土建工程方向研究。[通讯作者] 贾艳敏(yanminjia2008@126.com)

[基金项目]国家大学生创新训练计划项目(201410225041)

[收稿日期]2014-12-01