子模型在沥青混凝土桥面铺装荷载分析中的应用
黄志义, 葛倩如, 王金昌
(浙江大学 交通工程研究所, 浙江 杭州 310058)
子模型在沥青混凝土桥面铺装荷载分析中的应用
黄志义, 葛倩如, 王金昌
(浙江大学 交通工程研究所, 浙江 杭州310058)
[摘要]为获得在车辆局部荷载以及桥梁整体变形综合影响下,先简支后连续混凝土T梁桥沥青混凝土铺装层在不同接触条件下弯沉与应力应变的分布规律,建立局部梁段子模型进行分析。分析结果表明:采用子模型计算结果比整体模型小10%,满足精度要求。在连续体系中,受到桥梁横向结构显著影响,弯沉U2由中梁至边梁逐渐增加,边车道应力应变水平大于中车道;边车道荷位处,沥青下面层纵向剪应力S(23)值较上面层更大,纵向应变ε(33)随深度增加而递减。在滑移体系中,下面层S(23)迅速减小,但材料出现较大反向形变;且粘结刚度越大,S(23)与ε(33)值越大,受力特征越接近层间连续状态。
[关键词]子模型; 沥青混凝土桥面铺装; 水平荷载; 黏聚接触
0前言
由于材料性质上的特点以及环境因素的综合影响下,沥青混凝土桥面铺装层一直是水泥混凝土连续梁桥铺装体系的薄弱环节。目前,关于有限元法分析荷载作用下沥青桥面铺装层力学响应的研究较多。胡晓、苏凯[1]利用有限元法计算了偏载作用下,铺装层剪应力随不同结构形式与材料参数的变化。许涛、黄晓明[2]讨论了不同水平力系数、速度引起铺装层内各深度剪应力的变化规律。陆辉、孙立军[3]则从轮载作用形式角度出发,采用3种非均匀轮载形式进行轮胎与路面接触区域力学响应的有限元模拟。陈静云、李向阳[4]建立局部梁段有限元模型,分析竖向荷载作用下不同车速、不平度对铺装层变形与应力分布的影响。徐伟[5]从桥梁整体变形对桥面铺装作用以及面板局部变形特点两个维度进行分析。同时与建立的普通路面结构计算模型弯沉进行对比,从弯沉角度分析桥面铺装对沥青混凝土的性能要求。
在这些研究中,通常采用简化边界的有限元模型,忽略了桥跨结构的形式、支座类型以及整体竖向变形对沥青混凝土铺装层受力的影响。铺装层间的接触条件多假设为完全连续与水平滑动两种极端情况,这与不同阶段的实际受力状况不符。考虑到以往有限元分析中缺乏对模型边界条件的优化以及接触条件的深入研究,本文依托浙江省黄衢南高速上茨大桥工程,借助ABAQUS有限元软件的子模型技术[6]综合分析车辆局部荷载与桥梁整体变形作用下,不同接触条件对铺装层竖向弯沉、层内层间应力应变分布的影响,为沥青混凝土铺装层不同使用阶段以及重交通路段的结构形式的研究提供参考。
1子模型技术基本原理
子模型技术是采用分步分析的思路,以较小的计算规模获得精确的模拟结果的有限元分析技术[7-10]。在ANSYS、ABAQS 等有限元分析软件中,主要分析步骤为: ①整体模型分析:建立整体模型,可暂时忽略结构的一些构造细节;用较粗的网格对整体结构进行划分,获得所需分析的局部区域切割边界的位移响应; ②建立子模型:根据结构实际的尺寸、构造以及分析目标的要求,采用恰当的单元建立网格密度更大的精细模型; ③提供切割边界的插值:将整体分析所得切割边界位移响应,采用线性插值法自动施加到局部模型相应的位置; ④子模型分析:子模型原有的荷载和边界条件不变。
另外,为保证结果的准确性,模型边界应远离应力集中处,若条件不允许,则该处的计算结果不应予以采用。
2有限元建模
2.1依托工程简介
上茨大桥位于黄衢南高速与205接线路段,采用双向双车道设计。桥梁上部配跨形式为4×30 m+4×30 m预应力混凝土T梁,结构先简支后连续。单跨结构由五片梁组成,横截面尺寸见图1,单位m。T梁顶铺设厚度各为10 cm的混凝土调平层和沥青混凝土铺装层。沥青混凝土层采用的玄武岩纤维增强高粘沥青,具有粘度高、模量高、高温稳定性能好的特点[11]。
2.2整体模型结构与边界条件
整体模型纵向取单联桥梁跨度120 m,横向桥宽12 m。铺装层体系采用二次减缩积分六面体单元(C3D20R),根据材料不同分为三层:SMA-13层 、AC-16层和水泥混凝土调平层。暂时考虑层间为连续接触条件,即水泥混凝土调平层与沥青混凝土层以及沥青层间变形协调。模型Y轴为车辆行驶方向,X轴为桥宽方向,原点设在模型端部横向中点处。按照设计实际情况,在铺装层实体底部设置横纵两个方向的string线性梁单元(B31),以模拟桥梁结构的主梁与横隔板。模型所用材料假设为线弹性均质材料,模型计算参数设置见表1,其中H为厚度,E为弹性模量,ν为泊松比。
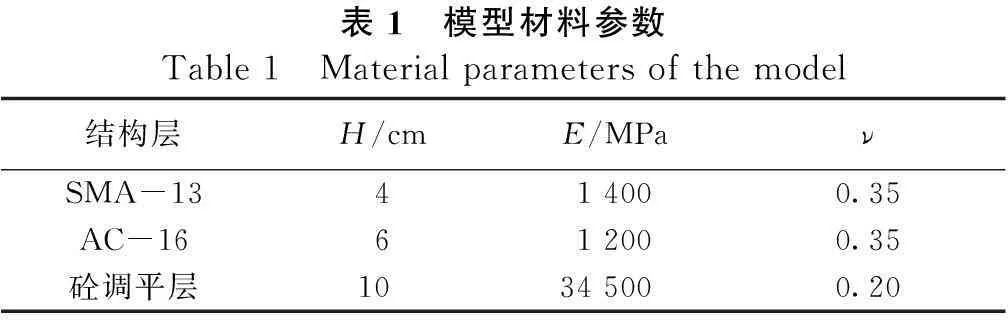
表1 模型材料参数Table1 Materialparametersofthemodel结构层H/cmE/MPaνSMA-13414000.35AC-16612000.35砼调平层10345000.20
模型边界条件参照连续梁混凝土桥的支座实际位置与类型进行设置。在固定支座处,约束竖向与水平位移;在所有活动支座处,约束竖向位移,横向活动支座、纵向活动支座还需分别约束纵向与横向的水平位移,具体布设情况如图1所示。

图1 T梁横断面与桥梁支座布置图Figure 1 T-beam transverse section and bridge bearings layout
2.3荷载分布形式与计算荷位的确定
模型荷载分为恒载与车辆荷活载两类。由于铺装层通常是在混凝土桥面板完全施工结束后才铺筑,因此桥面板自重对铺装层的受力无影响,不计入模型荷载。施加在模型上的恒载为铺装层的自重荷载。
在以往的桥面铺装分析中,常以公路设计标准BZZ-100作为车辆荷载设计。考虑到重型交通的发展以及桥面铺装层受力有别于路面结构,本文参考《公路桥涵设计通用规范JTG D60-2004》标准车辆荷载进行布设[12]。以矩形均布荷载模拟车轮接地压力;路表水平作用力,用车轮垂直荷载乘以车轮与路表之间的摩擦系数表示。考虑产生水平力最大的行驶工况,即在车辆制动时,水平力系数达到最大值0.5[13]的情况。加载车辆车型与轮胎接地形式如图2所示。

图2 加载车型与接地形式Figure 2 Loading vehicle type and contact mode
桥跨结构的挠度是反映其竖向变形特征对铺装层受力影响的主要指标。因此本文以桥跨结构在荷载作用下的竖向挠度作为计算荷位确定的控制因素。对于车辆荷载单次加载过程,可利用Midas软件进行双车道正载与偏载工况下的移动荷载分析,确定挠度的最不利位置。分析结果显示,在偏载工况下,最大挠度出现在边跨边梁中部。另外,其余三跨荷载引起最不利荷位处的挠度值较小,可以忽略不计。因此,在进行车辆荷载布设时,考虑边跨位置荷载即可,位置示意如图3(a)所示。
2.4子模型的建立
子模型的切割边界选取在有中、后轮同时作用的梁段两端横隔板处。材料属性、荷载以及接触条件不改变条件下,剔除模型中不关心的部分后,将子模型网格进一步的细化处理。在边界条件设置时,选用submodel边界功能,将整体模型中的分析结果自动施加的子模型相应位置。最终子模型总计21 736个单元,67 095个节点,如图3(b)所示。
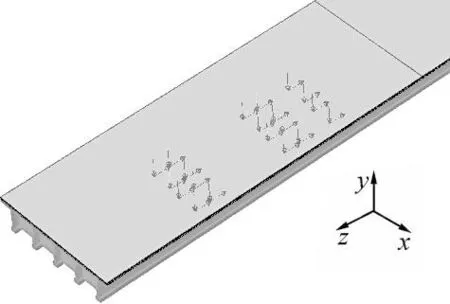

(a) 整体模型局部(b) 子模型
Figure 3Bridge structure+asphalt concrete deck pavement model
2.5子模型验证
为验证子模型的可靠性,对比分析整体模型与子模型荷载作用位置,弯沉U2与铺装表层的纵向水平剪应力S23两个力学指标计算结果上的差异。由中梁向边梁将各轴荷位分别依次编号1~4,以确定沿x轴方向的位置。结果输出位置为SMA表层中、后轴荷载作用点A处(见图2)。计算结果对比如表2所示可知:2种模型分析得到的U2与S23沿X与Y向的变化规律基本相同,并且计算结果处于同一量级。子模型力学指标计算结果相对偏小,这是因为子模型中不包含前轴荷载作用。但两者差值在10%以内,可以满足分析要求。因此,利用上述各参数建立子模型,采用较小的计算规模进行桥面铺装受力模拟是切实可行的。
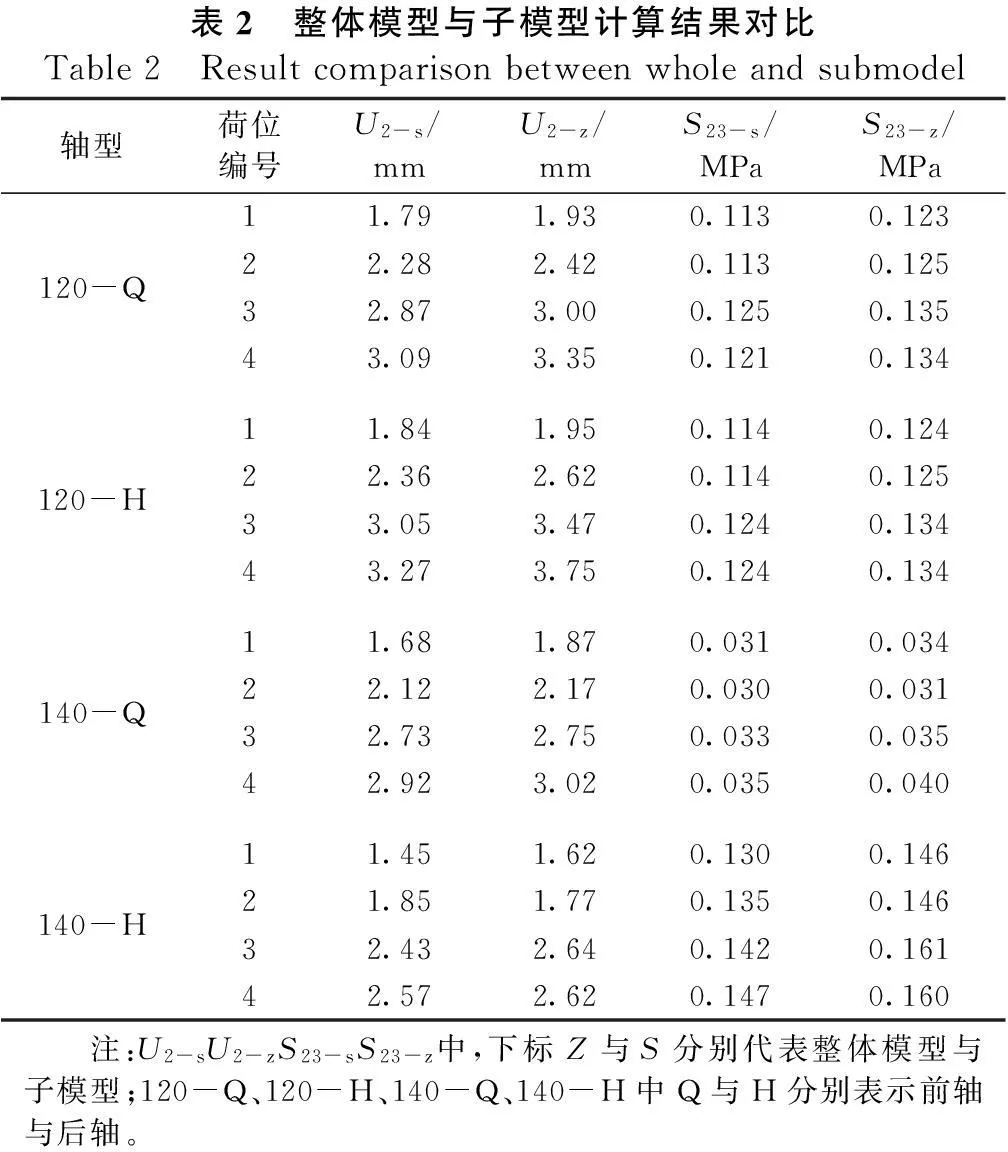
表2 整体模型与子模型计算结果对比Table2 Resultcomparisonbetweenwholeandsubmodel轴型荷位编号U2-s/mmU2-z/mmS23-s/MPaS23-z/MPa120-Q11.791.930.1130.12322.282.420.1130.12532.873.000.1250.13543.093.350.1210.134120-H11.841.950.1140.12422.362.620.1140.12533.053.470.1240.13443.273.750.1240.134140-Q11.681.870.0310.03422.122.170.0300.03132.732.750.0330.03542.923.020.0350.040140-H11.451.620.1300.14621.851.770.1350.14632.432.640.1420.16142.572.620.1470.160 注:U2-sU2-zS23-sS23-z中,下标Z与S分别代表整体模型与子模型;120-Q、120-H、140-Q、140-H中Q与H分别表示前轴与后轴。
3连续体系受力分析
在桥面铺装的使用初期,材料尚未出现破坏,各层粘结性能良好,不存在相对位移,可认为沥青铺装层为连续体系。因此,可利用上文所建变形协调铺装层的子模型计算结果,分析沥青铺装层使用初期的力学特征。基于铺装层常见病害以及材料的破坏原理,以各级轴载作用处的铺装层弯沉U2、纵向水平剪应力S23以及纵向拉弯应变ε33作为主要力学指标,分析沥青混凝土铺装层各深度的分布规律。
3.1弯沉U2沿桥面横向变化规律
各级荷载作用下沿X轴方向的弯沉盆,如图4所示可知:当X方向距离相同时,U2值在120-H轴位最大,140-H轴位最小,这也说明弯沉的大小与荷载等级的大小没有直接关系。各级荷载作用处,U2沿X方向的变化规律相同:U2值整体上随距离变大而增大,但在X=3.6 m轮胎接地处由于应力集中,弯沉值出现了突变。这反映出桥梁横向的悬臂作用显著:随着距离增加,桥梁整体变形对弯沉U2值贡献变大;铺装层弯沉是其局部与桥梁整体受力共同作用的结果,两个缺一不可。

图4 各级荷载作用处沿X方向弯沉盆Figure 4 Deflection basins of different loading positions along X
3.2纵向水平剪应力S23沿深度变化规律
各级荷载作用处,纵向水平剪应力S23沿深度h的计算结果见图5~图8。

图5 120 kN前轴处S23随深度变化Figure 5 Variation of S23 with depth under 120 kN front axle
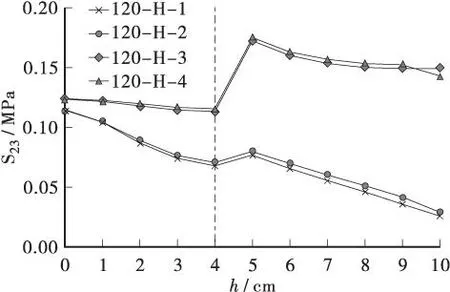
图6 120 kN后轴处S23随深度变化Figure 6 Variation of S23 with depth under120 kN rear axle

图7 140 kN前轴处S23随深度变化Figure 7 Variation of S23 with depth under 140 kN front axle
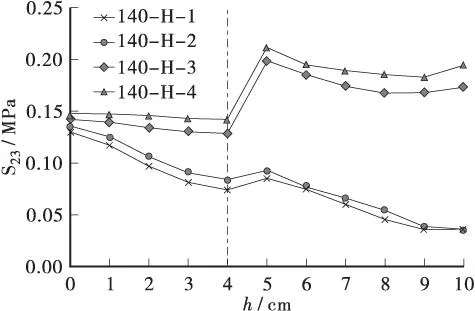
图8 140 kN后轴处S23随深度变化Figure 8 Variation of S23 with depth under140 kN rear axle
由图可看出各轴位纵向剪应力S23最大值皆出现在边车道车轮荷载作用处(对应3、4荷位),深度约为5 cm的位置。且以140-H-4处的S23最大,达到0.21 MPa。同一轴位边车道与边车道(对应1、2荷位)处,S23随深度的变化呈现两种不同的规律:边车道荷位S23在同一结构层中受到深度的影响较小,受力较均匀,仅在深度为4~5 cm小范围内随深度快速增大;中车道荷位S23值随深度增加整体逐渐减小。且在同一深度,边车道作用处的应力大于中车道车道荷载。
综上可知:铺装层内纵向剪应力S23同样受到桥梁横向结构的显著影响,边车道下面层S23值普遍较大,应以该处作为抗剪设计重点考虑的位置。
3.3纵向应变ε33沿深度变化规律
考虑到水平力的方向,并由有关计算结果显示,各方向的应变值以纵向应变ε33最大,其沿深度变化的计算结果如表3所示。
边车道荷位各深处应变值为正,即变形方向与行车方向始终一致。ε33值随深度增加迅速减小,最大值出现于140-Q-3铺装层表面,到达180 με。对于中车道荷位,ε33值波动较大,上面层出现与行车方向相反的变形,以140-H-1最大达到32 με;在下面层底部,正向应变随深度增加有所增加,以140-Q-2荷位下面层层底计算值最大,到达39 με。

表3 各级荷位处ε33/(με)沿深度的变化Table3 Variationofε33withdepthunderdifferentloadingpositionsh/cm荷位编号120-Q120-H140-Q140-H1234123412341234041169151-16-10170117-14-7189159-32-16172892713131113-321328907146115-14-8136624142010689-51010772101511687-3-2111476137665-7-48852-8-48156-16-208836812166457811784681366453-277331034386355293071413439644426207230
可以看出轴载等级与纵向变形无直接关系。边车道荷位的应变水平普遍大于中车道,且随深度的应变值递减的规律显著。由于上面层的拉弯组合应变值较大,应注意上面层沥青混凝土材料的抗张拉开裂性能设计。
4滑移体系受力分析
在通车运营阶段,由于车辆重复荷载的振动、冲击、拉伸和剪切等作用[14],铺装结构层与桥面板之间粘结力逐渐减弱,甚至出现局部滑移的现象,连续体系转变成滑移体系。为了使分析更加接近实际受力状态,本文利用ABAQUS中的黏聚接触[15],模拟滑移体系结构层间的接触状态。分析黏结刚度K[6]分别取为1、10、100 MPa·m-1时,铺装层纵向应变ε33随深度的变化,并与连续体系(对应接触条件用Tie表示)计算结果相比较。计算荷位采用上文分析连续体系时获得的S23与ε33量值最大的位置:140-H-4与140-Q-3,模型其余条件与参数不变。计算结果如图9,图10所示。
由图9可知:同一深度,连续体系计算值最大;粘结刚度越大,S23值越接近最大值。3种粘结刚度的S23随深度的变化规律一致:上面层缓慢减小,从深度4 cm起小幅攀升至5 cm。深度5 cm以下部分随着深度的增加衰减迅速,直至下面层层底剪应力接近零。由图10可知:同一深度,粘结刚度越大,ε33值也越大,其受力也越接近层间连续状态。ε33代数值逐渐减小,上面层内为正应变,下面层出现反向变形,在下面层层底部达到最大。且当粘结刚度越小,ε33反向变形越显著。
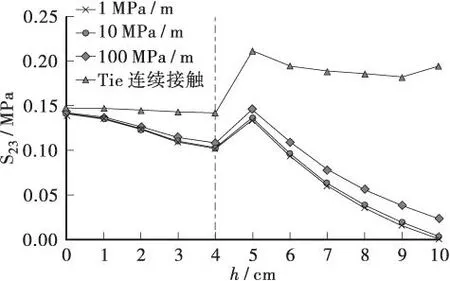
图9 不同接触条件下的S23随深度的变化Figure 9 Variation of S23 with depth under different interactions
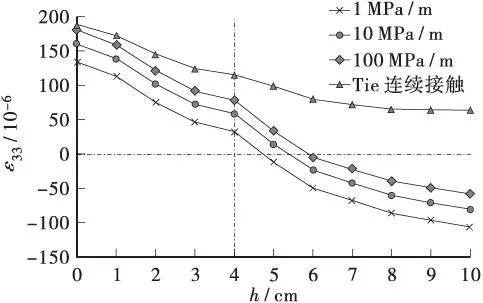
图10 不同接触条件下的ε33随深度的变化Figure 10 Variation of ε33with depth under different interactions
总体而言,滑移体系中应力应变分布形式与连续体系相差较大。一方面滑移行为释放了材料内部变形能,使得铺装层尤其是下面层应力迅速减小。另一方面,下面层反方向变形的增大,重复荷载作用必定造成该处沥青混合料的疲劳破坏。因此,需注意下面层材料的抗疲劳性能设计。
5结论
a. 整体模型与子模型分析得到的弯沉U2与纵向水平剪应力S23沿行车方向以及桥面横向的变化规律相同。两者差值在10%之内,采用计算规模较小的子模型进行混凝土连续梁桥沥青铺装层受力分析切实可行。
b. 子模型进行铺装层连续体系分析得到以下结论: ①铺装层弯沉U2与荷载等级的大小无直接关系,是局部与桥梁整体受力共同作用的结果,且由中梁至边梁,桥梁整体变形对U2值贡献变大。 ②纵向剪应力S23同样受到桥梁横向结构的显著影响,边车道下面层S23值普遍较大,最大值出现于140-H-4荷位处沥青铺装层下面层,应以该处作为抗剪设计控制位置。 ③边车道荷位纵向应变ε33的应变水平普遍大于中车道,且随深度递减的规律显著,最大值出现于140-Q-3荷位铺装层表面。上面层的拉弯组合应变值较大,应注意沥青上面层的抗张拉开裂性能设计。
c. 滑移体系中应力应变分布形式与连续体系相差较大,下面层应力迅速减小,但出现较大的反向变形,应注意该结构层沥青混合料的抗疲劳性能设计。另外,粘结刚度越大,S23与ε33值越大,其受力也越接近层间连续状态。
[参考文献]
[1]胡晓,苏凯,胡小弟,等.水泥混凝土桥桥面沥青铺装层的有限元分析[J].公路交通科技,2007,24(03):5~9+14.
[2]许涛,黄晓明,高雪池.移动荷载作用下沥青混凝土桥面铺装层动力响应分析[J].公路交通科技,2007,24(10):6-10.
[3]陆辉,孙立军,张宏超.非均布轮载作用下沥青路面应力分析[J].同济大学学报:自然科学版,2001,29(06):672-676.
[4]陈静云,李向阳.基于耦合的沥青混凝土桥面铺装动力响应[J].山东交通学院学报,2012,20(04):36-42.
[5]徐伟,白海涛,张肖宁.大跨径混凝土斜拉桥桥面铺装力学数值模拟分析[J].哈尔滨工业大学学报,2003,35(06):750-754.
[6]庄茁,张帆,岑松.ABAQUS非线性有限元分析与实例[M].北京:科学出版社,2005.
[7]李爱群,王浩.子模型法在超大跨悬索桥钢箱梁应力分析中的应用[J].工程力学,2007,24(02):80-84.
[8]车轶,宋玉普.混凝土高拱坝孔口三维非线性分析[J].大连理工大学学报,2003,43(02):218-222.
[9]王珍君,侯炳麟.钢轨轨头三维应力有限元分析[J].中国铁道科学,2000,21(04):68-74.
[10]GIGLIO M.FEM submodelling fatigue analysis of a complex helicopter component [J].International Journal of Fatigue.1999,21(05):445-455.
[11]钟明键,彭响兰.玄武岩纤维增强沥青混合料性能试验研究[J].公路工程,2013,38(05):157-160.
[12]JTG D60~2004,公路桥涵设计通用规范[S].
[13]JTG D50~2006,公路沥青路面设计规范[S].
[14]王京元.水泥混凝土桥沥青混凝土桥面铺装早期病害原因分析和结构设计方法[D].大连:大连理工大学,2003.
[15]罗圆月.BFRP筋连续配筋复合式路面结构分析及使用寿命探索[D].杭州:浙江大学,2014.
Load Analysis on Asphalt Concrete Deck Pavement With Submodel Method
HUANG Zhiyi, GE Qianru, WANG Jinchang
(Institute of Transportation Engineering, Zhejiang University, Hangzhou, Zhejiang 310058, China)
[Abstract]In order to get the deflection and stress-stain distribution in the asphalt concrete deck pavement of simply supported-continuous T-beam bridge under the comprehensive effect of local loading and bridge deformation,the partial beam-segment submodel was built.The analyses indicate that the result of submodel is 10% smaller than the whole model which meets the requirement of precision.In the continuous system of deck pavement,U2(deflection)increases from center to edge beam .And the stress and strain of edge lanes are much higher than the central lanes under the significant effect of transverse structure of bridge. S(23)(longitudinal shear stress)in the asphalt lower layer of edge-lanes is much higher than the upper layer.And ε(33)(longitudinal strain)of edge-lanes decreases with the increase of depth.In the partial slip system of deck pavement,S(23) of lower layer rapid decreases but the great reverse deformation occurs in the material.The higher the bonding stiffness is,the higher S(23) and ε(33)are and more close to continuous system the mechanics characteristics.
[Key words]submodel method; asphalt concrete deck pavement; horizontal load; cohesive interaction
[中图分类号]U 443.33
[文献标识码]A
[文章编号]1674-0610(2016)01-0157-06
[作者简介]黄志义(1957-),男,福建莆田人,教授,从事道路工程设计与材料试验研究。
[基金项目]浙江省交通运输厅科技计划项目(2013H286)
[收稿日期]2014-11-10

