薄壁高墩连续刚构桥的稳定分析

张建军， 钟　凯， 杨美良， 段志岳

(1.中铁十二局集团第七工程有限公司， 湖南 长沙　410004；　2.湖南省武靖高速公路建设开发有限公司， 湖南 武冈　422400；　3.长沙理工大学 土木与建筑学院， 湖南 长沙　410001)



薄壁高墩连续刚构桥的稳定分析

张建军1， 钟凯2， 杨美良3， 段志岳3

(1.中铁十二局集团第七工程有限公司， 湖南 长沙410004；2.湖南省武靖高速公路建设开发有限公司， 湖南 武冈422400；3.长沙理工大学 土木与建筑学院， 湖南 长沙410001)

[摘要]利用Midas civil有限元软件，对杨家湾大桥15#薄壁墩最高裸墩、最大悬臂阶段和成桥3种状态进行了稳定分析，给出了结构的失稳模态和荷载—位移曲线，得到了各工况下的屈曲荷载和稳定安全系数。最高裸墩、最大悬臂和成桥3状态下，最大悬臂状态的稳定值最小，第一阶特征值为15.67，最大悬臂状态为稳定控制的最不利阶段。考虑几何非线性影响时，最不利工况下各阶稳定值下降，墩底轴力和墩顶位移增大，荷载与位移呈非线性变化，特别是在最大悬臂状态变化更加明显。高墩大跨连续刚构桥梁的稳定性主要跟施工节段有关，施工时的风荷载、温度荷载对结构的稳定影响小，但挂篮跌落对结构稳定性的影响大；施工过程中一定要加强管理，防止挂篮意外跌落，避免出现梁段重量不均或者加载不均匀，确保施工安全。

[关键词]薄壁高墩； 连刚构桥； 屈曲模态； 几何非线性； 稳定分析

1工程概况

广西资源(梅溪)至兴安高速公路杨家湾大桥全长740.1 m，主桥上部结构为50 m+90 m+50 m预应力混凝土变截面连续刚构桥(见图1)，三向预应力单箱双室箱形主梁顶板宽12.75 m，底板宽9 m，主墩处梁高5.5 m，跨中和边跨现浇段梁高2.6 m，采用挂篮悬臂浇筑法施工。下部结构14号过渡墩采用矩形空心墩，15、16号桥墩采用双肢薄壁实心墩，其中15#主墩墩高达75 m。该桥具有薄壁、墩高的特点，墩的稳定性问题尤为突出。

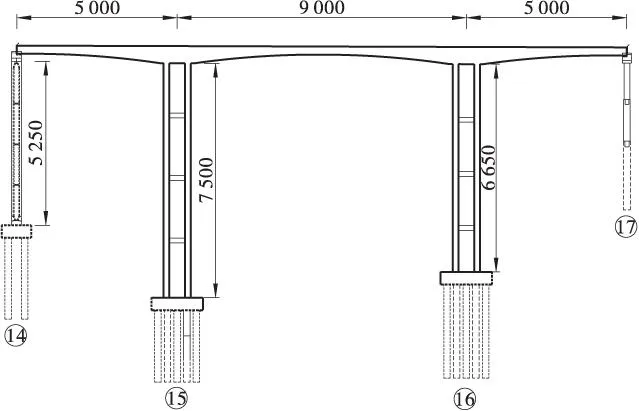
图1　连续刚构桥跨布置示意图(单位： m)Figure 1　The bridge span arrangement diagram of continuous 　rigid frame bridge(unit： m)

2稳定分析理论及方法

结构失稳是指在外力作用下结构的平衡状态丧失，稍有扰动变形迅速增大，最后使结构遭到破坏[1]。稳定问题分为第一类稳定问题和第二类稳定问题。第一类稳定问题是平衡分支失稳，即结构达到临界荷载时还存在除原平衡状态外其他平衡状态，这一临界荷载是使结构原有平衡形式保持稳定的最大荷载，也是使结构产生新的平衡形式的最小荷载，通过计算结构的几何刚度矩阵的特征值，求得最小特征值即稳定系数λ，得到的相应特征向量就是失稳模态。第二类稳定问题是极值点失稳问题，即结构从初始平衡状态随荷载不断增加，在应力较大的区域出现塑性变形，结构变形迅速增大，当荷载达到一定值时，即使不再增加，结构的变形也迅速增大，这个临界荷载实质就是结构的极限荷载。高墩连续刚构桥属压弯构件，其稳定性问题属于典型的极值点失稳，即属于第二类失稳问题。

2.1结构线性稳定分析理论

桥梁结构引入轴向力的平衡方程为：

(1)

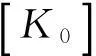
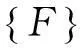
(2)

(3)

同时满足式(2)和式(3)的条件是：

(4)

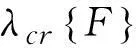
2.2几何非线性稳定分析方法

分析的整个过程中，单元发生的应变和单元位移以及单元之间节点力所取方向均以初始位形(即t=0时刻)作为参考位形，并且参考位形保持不变，由此建立的有限元公式即为全拉格朗日列式，即T.L列式。其有限元增量方程为：

(5)

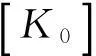
(6)

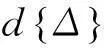
在建立T+ΔT的有限元平衡方程，选择最终那个已经完成的平衡状态，并以增量步开始时的T时刻的形状为参考位形，构成修正的拉格朗日列式，即为U.L列式。其有限元增量方程为：

(7)

3稳定计算及结果分析

3.1模型的建立

运用Midas civil软件建立杨家湾大桥结构模型，15#桥墩裸墩共划分33个单元，32个节点；施工阶段最大悬臂状态共划分68个单元，67个节点；成桥阶段共划分138个单元，137个节点，最大模型及单元划分见图2。

图2　杨家湾大桥全桥单元模型及单元划分Figure 2　The element model and element generation of 　yang jia wan bridge

3.2线性稳定性分析

3.2.1最高裸墩状态

裸墩在施工过程中可能出现的荷载有： ①主墩自重； ②横向风荷载； ③纵向风荷载； ④温度梯度荷载。风荷载、温度梯度荷载的取值参考文献[2]，纵向风压取横向风压的70%。

对上述荷载进行组合得出：

工况1：①；

工况2：①+②；

工况3：①+②+③；

工况4：①+②+③+④。

由上述荷载工况，可分别计算得到15#主墩的特征值见表1，最不利工况下失稳模态见图3。

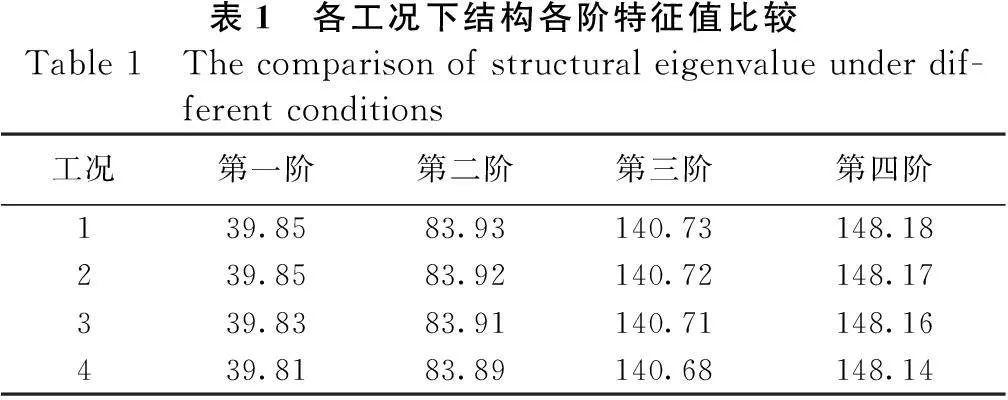
表1 各工况下结构各阶特征值比较Table1 Thecomparisonofstructuraleigenvalueunderdif-ferentconditions工况第一阶第二阶第三阶第四阶139.8583.93140.73148.18239.8583.92140.72148.17339.8383.91140.71148.16439.8183.89140.68148.14

(a) 一阶模态失稳图(b) 二阶模态失稳图(c) 三阶模态失稳图(d) 四阶模态失稳图

图3裸墩阶段最不利工况下屈曲模态图

Figure 3The buckling mode of the pier state under the most unfavorable conditions

由表1可知：该桥裸墩状态下特征值较大，纵横向风荷载和温度荷载对裸墩的稳定性几乎没有影响。这是因为风荷载的大小跟墩体自重比起来很小，几乎可忽略不计。

3.2.2最大悬臂状态

最大悬臂状态稳定性分析中可能出现的荷载有：

①结构自重； ②施工荷载，共计850 kN； ③浇筑不同步荷载，一侧增大5%，另一侧减少5%； ④一侧挂篮跌落；动力放大系数为2.0，即坠落一侧反向施加2倍的挂篮自重； ⑤横向风荷载； ⑥纵向风荷载； ⑦温度梯度荷载。对上述荷载进行组合得出：

工况1：①+②+⑤；

工况2：①+②+③+⑤；

工况3：①+③+④+⑤；

工况4：①+③+④+⑤+⑥+⑦。

根据上述荷载工况，可得到主墩最大悬臂状态下的稳定特征值，如表2所示。最不利工况下失稳模态见图4。

从最大悬臂状态稳定性分析结果中可知：此阶段的稳定性较裸墩自体稳定性明显降低，最不利工况下一阶特征值仅为15.67，挂篮跌落和浇筑不同步荷载对高墩的稳定产生较大的影响。

表2 各工况下结构各阶特征值比较Table2 Thecomparisonofstructuraleigenvalueunderdif-ferentconditions工况号一阶二阶三阶四阶119.7141.5750.0172.15219.0540.2548.5770.29315.9232.2839.3656.69415.6731.6538.6754.56

(a) 一阶模态失稳图(b) 二阶模态失稳图

(c) 三阶模态失稳图(d) 四阶模态失稳图

Figure 4The buckling mode of the longest cantilever state under the most unfavorable condition

3.2.3成桥状态

成桥状态稳定性分析中可能出现的荷载有： ①结构自重(包括二期恒载)； ②风荷载； ③温度荷载：按照设计资料，取全桥整体升温或降温25 ℃；最不利荷载工况为：①+②+③，计算结果见表3，失稳模态见图5。

表3 结构各阶特征值比较Table3 Thecomparisonofstructuraleigenvalue荷载工况稳定特征值失稳模态①+②+③一阶二阶三阶四阶21.6738.3749.5463.54面内失稳

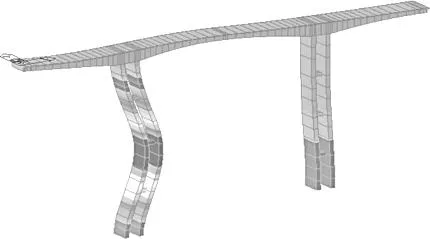
(a) 一阶模态失稳图(b) 二阶模态失稳图

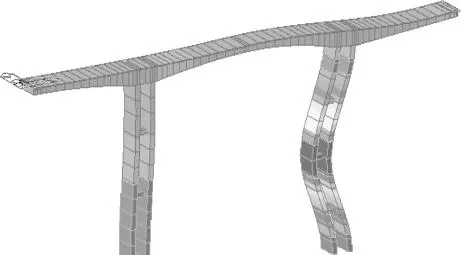
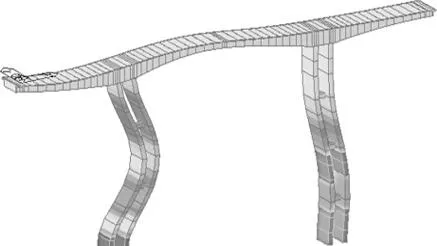
(c) 三阶模态失稳图(d) 四阶模态失稳图

Figure 5The buckling mode of the completed bridge under the most unfavorable condition

3.2.4线性稳定结果分析

分析表1～表3和有限元计算结果得到以下结论：

① 高墩大跨连续刚构桥梁的稳定性主要跟施工节段有关，施工时的风载、温度荷载对结构稳定性的影响小，但挂篮跌落和不同步荷载对结构稳定性的影响大。

② 裸墩、最大悬臂和成桥3种状态下，各阶失稳特征值都较大，最大悬臂状态的稳定值最小，其稳定性最差，最大悬臂施工阶段为稳定控制的最不利阶段，第一阶失稳荷载因子最小值为15.67，说明结构稳定性较好，满足设计和规范[3]要求。

3.3几何非线性稳定性分析

以15#墩为研究对象，分别对裸墩状态、最大悬臂状态和成桥状态进行几何非线性稳定分析，荷载工况取线性稳定性分析时的最不利荷载工况，计算结果见表4。

由表4可得：最不利荷载作用下，3种状态在考虑几何非线性因素的情况下，各阶稳定值均下降，说明线性稳定分析得到非保守的结果，是承载能力的上限。同时计算表明荷载与墩顶位移呈非线性变化关系，在所施加荷载范围内没有出现失稳现象，且考虑几何非线性的稳定特征值仍较大，满足设计和规范要求；随着阶数升高，几何非线性对稳定性的影响更为明显。

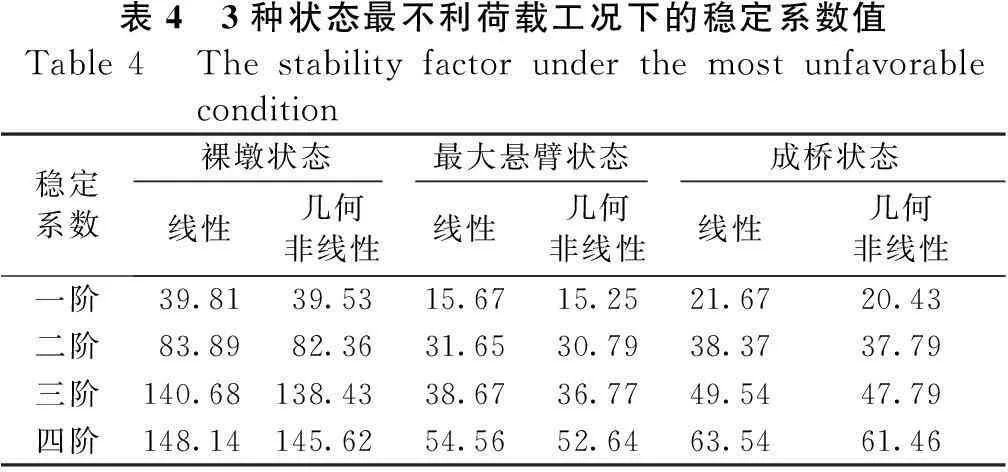
表4 3种状态最不利荷载工况下的稳定系数值Table4 Thestabilityfactorunderthemostunfavorablecondition稳定系数裸墩状态最大悬臂状态成桥状态线性几何非线性线性几何非线性线性几何非线性一阶39.8139.5315.6715.2521.6720.43二阶83.8982.3631.6530.7938.3737.79三阶140.68138.4338.6736.7749.5447.79四阶148.14145.6254.5652.6463.5461.46

考虑几何非线性影响的位移如图6和表5。由图6和表5可知：在各个施工状态，墩底轴力和墩顶最大位移在考虑几何非线性时明显比不考虑几何非线性时要大，特别是在最大悬臂状态，墩底轴力和墩顶位移变化更加明显。

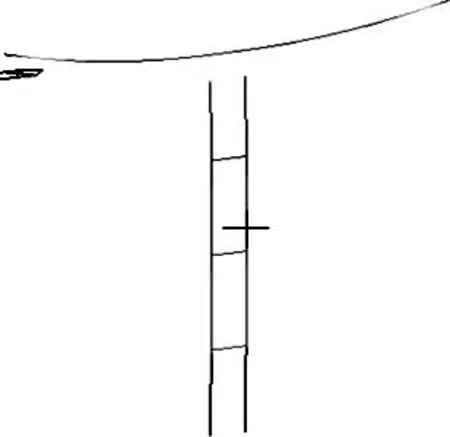
(a) 裸墩位移图(b) 最大悬臂状态位移图(c) 成桥状态位移图

图6考虑几何非线性影响的位移图

Figure 6The displacement of considering the geometric nonlinearity

表5 考虑几何非线性墩底轴力值和墩顶位移值Table5 Consideringthegeometricnonlinearblockbottomaxialforcevalueandthepiertopdisplacementval-ues桥梁结构状态墩底轴力/kN墩顶最大位移/cm15#墩左肢15#右肢不考虑几何非线性考虑几何非线性裸墩状态30044322130.860.92最大悬臂状态54017518371.431.94成桥状态66914538063.864.23

4结论和建议

本文通过对杨家湾大桥的施工和成桥阶段的线性及非线性稳定分析可以得出如下结论：

① 计算中结构的第一阶失稳荷载因子最小值为15.67，说明结构稳定性满足设计和规范要求。考虑几何非线性影响的稳定系数均比特征值低，说明线性稳定分析得到非保守的结果，是承载能力的上限。

② 裸墩状态、最大悬臂状态和成桥状态下，最大悬臂状态的稳定值最小，说明最大悬臂施工阶段为稳定控制的最不利阶段。

③ 在各个施工状态，墩底轴力和墩顶最大位移在考虑几何非线性时比不考虑几何非线性时要大，特别是在最大悬臂状态，墩底轴力和墩顶位移变化较为明显，故将几何非线性纳入考虑范围以内是有必要的。

④ 高墩大跨连续刚构桥梁的稳定性主要跟施工节段有关，施工时的风载、温度荷载对结构稳定性的影响小，但挂篮跌落对结构稳定性的影响大。施工过程中一定要加强管理，防止挂篮意外跌落，避免出现梁段重量不均或者加载不均匀，确保桥梁施工安全。

[参考文献]

[1]李国豪.桥梁结构稳定与振动[M].北京：中国铁道出版社，1992.

[2]JTG D60-2004，公路桥涵设计通用规范[S].

[3]JTG D62-2004，公路钢筋混凝土及预应力混凝土桥涵设计规范[S].

Stability Analysis of Thin-Walled High Piers Continuous Rigid-Frame bridge

ZHANG Jianjun1， ZHONG Kai2， YANG Meiliang3， DUAN Zhiyue3

(1.The 7th Engineering Co.， Ltd. of China Railway 12 th Bureau Group， Changsha， hunan 410004， China；2.Hunan Province Wu-Jing Highway Construction & Development Co. Ltd. Wugang， Hunan 422400， China；3.School of Civil Engineering and Architecture， Changsha University of Sience and Technology， Changsha， Hunan 410001， China)

[Abstract]By utilizing the finite element software Midascivil，the stability of the highestbare pier，the stability of the longest cantilever during construction and the stability in complete stage of the Yang Jia Wan bridge 15# pier are analyzed，the buckling modeand the load-displacement curve are obtained，the buckling load and the stabilitysafety factor ofall conditions aredrown.In the three conditions of the highest bare pier，the longest cantilever and thecompleted bridge，the value of stability is lowest in the state of the highest bare pier， and the eigenvalue is 15.67 in the first stage.The state of the longest cantilever is the most unfavorable stage for stability control.When considering the geometric nonlinearity，in the most unfavorable conditions，the value of stability in each stage would decrease，and the axial force on the bottom of pier and the displacement on the top of pier would increase，and the load and displacement act as nonlinear changes，especially in the longest cantilever state.The stability of the high-pier and long-span continuous rigid frame bridge is mainly related with construction segments.The wind load and temperature load have low influences on structure stability.However，the dropping hanging baskets have a great impact on structure stability.Therefore，management should be strengthened to prevent the falling hanging baskets during the process of construction.And in order to ensure the construction safety，uneven weight of beams or uneven loads also should be avoided.

[Key words]thin-walled pier； continuous rigid-frame bridge； the buckling mode； geometrically nonlinear； stability analysis

[中图分类号]U 448.23

[文献标识码]A

[文章编号]1674-0610(2016)01-0139-04

[作者简介]张建军(1976-)，男，湖南岳阳人，高级工程师，从事高速公路建设与管理工作。

[基金项目]湖南省科技厅项目(2014FJ3066)；湖南交通科技创新项目(201452)

[收稿日期]2015-10-20