汽轮机非线性间隙气流激振力作用下含裂纹转子的振动特性研究

瓮　雷， 杨自春， 曹跃云(1.海军工程大学 舰船高温结构复合材料研究室，武汉　430033； 2.海军工程大学 动力工程学院， 武汉　430033)



汽轮机非线性间隙气流激振力作用下含裂纹转子的振动特性研究

瓮雷1,2， 杨自春1,2， 曹跃云1,2(1.海军工程大学 舰船高温结构复合材料研究室，武汉430033； 2.海军工程大学 动力工程学院， 武汉430033)

摘要：建立了在汽轮机非线性间隙气流激振力作用下裂纹转子-轴承系统的动力学分析模型，并采用数值积分方法研究此类裂纹转子系统的分岔与混沌特性。利用Poincare截面和分岔图的变化分析汽轮机非线性间隙气流激振力和裂纹深度对系统振动响应特性的影响。分析结果表明：汽轮机非线性间隙气流激振力会使得系统的周期性运动状态提前，且混沌区域发生明显的减小；在浅裂纹时，汽轮机非线性间隙气流激振力对系统的响应起主导作用，且在超临界转速区域出现周期8运动；随着裂纹深度的增加，系统运动的混沌区域逐渐减小几乎消失，在超临界转速区域的逆周期运动演变为较长的周期3运动。研究结果可以作为含裂纹转子在汽轮机非线性间隙气流激振力作用下耦合故障发生的典型特征，也可作为此类耦合故障诊断的依据。

关键词：转子；汽轮机非线性间隙气流激振力；裂纹；非线性振动

转子是船用汽轮机组的关键部件，其工作环境非常恶劣，长期处于高温介质中高速旋转。它承受着由转子本身和叶片质量的离心力引起的应力、温度分布不均匀引起的热应力、传递作用在叶片上的气流力产生的扭矩、工质的压力和自身重量产生的弯矩等[1-2]，逐渐形成疲劳裂纹源进而扩展，裂纹会导致转轴刚度降低，从而引起转子横向振动幅值变大，形成运行故障进而影响机组正常工作，严重影响飞机和船舶在航率和安全性。引起转子异常振动或振动过大的原因有很多，转轴裂纹是主要原因之一。

近年来，国内外很多学者对裂纹故障转子系统的复杂动力学行为进行了研究分析。Meng等[3]讨论了裂纹深度、裂纹位置、转速与质量偏心对Jeffcott转子振动响应各阶谐波分量、轨道圆度的影响。Zuo等[4]建立了含初始弯曲裂纹转子的动力学模型,讨论了系统振动特性随刚度、质量偏心、初始弯曲的变化。李振平[5]等在考虑非线性油膜力的基础上研究了裂纹转子的动力学行为。张靖等[6]在考虑非线性涡动与圆盘的摆振运动对裂纹转子运动的影响的基础上，建立了裂纹转子的运动微分方程，分析了系统运动特性随裂纹深度、裂纹角的变化。于涛等[11]从断裂力学理论出发，通过建立的裂纹转子模型分析了双裂纹转子系统的非线性动力学特性。岳二团等[12]研究了气隙偏心下永磁电机转子系统的震动特性，详细讨论了不同偏心以及负载类型对转子系统振动特性的影响。Sinou等[8]借助有限元方法研究了裂纹转子的非线性动力学特性。曾复等[9-10]利用数值方法研究了带裂纹Jeffcott转子的分盆与混沌特性。于海等[11]采用改进的POD方法分析研究了多自由度裂纹转子系统的非线性动力学特性。岳二团等[12]研究了气隙偏心下永磁电机转子系统的震动特性，详细讨论了不同偏心以及负载类型对转子系统振动特性的影响。黄志伟等[13]研究了不平衡磁拉力作用下裂纹转子的分岔与混沌特性。Sinou[14]考虑裂纹深度、位置及轴旋转速度的影响，对裂纹转子系统的稳定性进行了研究分析。。邹剑等[15]基于简单铰链裂纹模型，建立了含初始弯曲裂纹转子的无量纲动力学方程，可适用于稳态、瞬态、非线性等不同运动状态下、不同系统参数情形下裂纹转子的振动分析，采用Floquet理论分析了含初始弯曲裂纹转子的稳定性，讨论了不同的刚度变化、阻尼比对系统稳定性的影响，可为裂纹转子识别提供依据。Cao[16]研究了含分数阶阻尼的裂纹转子系统的非线性动力学行为。Guo等[17]研究了含有横向呼吸裂纹的Jeffcott转子系统，采用Floquet理论在考虑转子的裂纹深度和旋转速度的基础上研究了转子系统的稳定性。这些文献在对裂纹转子非线性动力学行为研究取得了非常有价值的结论和成果。

然而在工程实际中，转子-轴承系统更加复杂，汽轮机叶轮偏心造成圆周方向叶尖间隙的不均匀分布，同一级中各叶片上的气动力就不相等，叶片上的周向气动力除合成一个转矩外，还合成一个作用于转子轴心的横向力。这一横向力随叶轮偏心距的增大而增大，是转子的一个自激振动，该力引起转子的进动，在一定条件下引起转子的失稳[18-20]。转子系统一旦发生故障，就可能有多种故障同时并存，故障之间的相互影响使得系统的动力学行为更加复杂。尽管已经有很多学者研究了裂纹或气流激振力对转子系统动力学行为的影响，但到目前为止，对于汽轮机非线性间隙气流激振力和裂纹耦合故障下的转子非线性动力学研究尚且没有进行研究。因此，本文建立了在汽轮机非线性间隙气流激振力作用下裂纹转子的动力学分析模型，考虑了裂纹交叉刚度和综合开闭规律模型，通过数值方法研究了汽轮机非线性间隙气流激振力及裂纹深度对转子系统运动的影响及非线性动力学行为，为实际转子—轴承系统的故障诊断和稳定运行提供参考。

1转子轴承系统的数学模型

本文以含有裂纹故障的对称刚性油膜支承的转子-轴承系统作为研究对象，忽略扭转振动和陀螺力矩，只考虑转子的横向振动，如图1所示，研究在汽轮机非线性间隙气流激振力作用下的非线性动态响应。其中O1、O2分别为轴承内瓦和转子几何中心，O3为转子质心；转子两端由半径为R、长为L的滑动轴承支承，m1、c1和m2、c2分别为转子在轴承处和圆盘处的等效集中质量和结构阻尼，e为圆盘的质量偏心，Fx、Fy为非线性油膜力。转子与轴承之间为无质量弹性轴，在轴中间有深度为a的弓形横向裂纹。

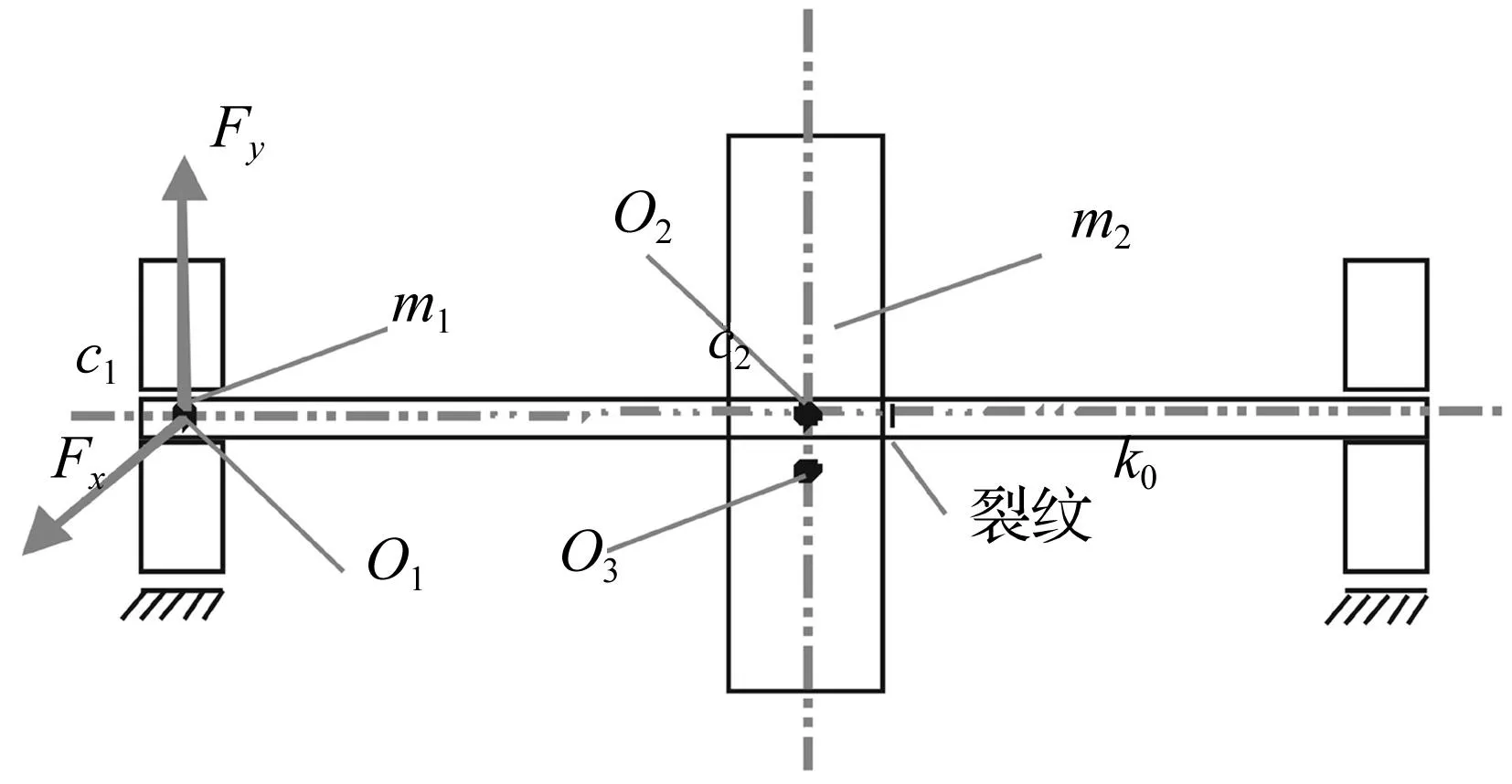
图1　油膜支承裂纹转子系统示意图Fig.1 A schematic of the rotor system

1.1非线性间隙气流激振力模型

本文以某型汽轮机转子为研究对象，系统结构及受到的气流激振力如图2所示。fax、fay为气流激振力Fa在x,y方向的分力。非线性气流激振力采用文献[18]中无量纲激振力模型：

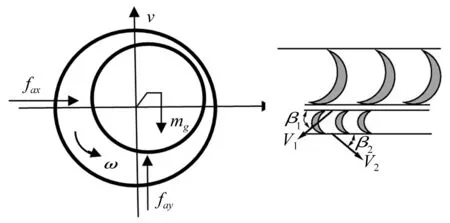
图2　系统受力图及气流在静、动叶片间流动示意图Fig.2 Loading diagram of the system

(1)

式中：

(2)

1.2裂纹刚度模型

转子裂纹轴横断面如图3所示，转子轴在无裂纹时的刚度为k0,kxx为x方向的刚度；kxy、kyx为x,y方向交叉的刚度；裂纹在ξ方向和η方向的刚度变化量为kξ和kη；ω为转速；β为不平衡量与裂纹法向的夹角。转子系统的刚度矩阵无量纲形式可表示为[21]：

图3　转子裂纹轴横断面示意图Fig.3 The model of the crack on the shaft

(3)

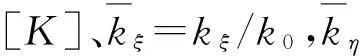
(4)

开闭函数当a/R<0.5时采用GASCH的铰链弹簧模型，a/R≥0.5时采用MAYES提出的裂纹模型[22]，开闭函数表达式如下：

(5)

1.3油膜力模型

本文采用短轴承模型[23]，短轴承在坐标轴x,y两个方向上的无量纲油膜力为：

式中：

G(x,y,α)=

1.4转子-轴承系统运动微分方程

设转子左端轴承处的径向位移为x1、y1；转盘处的径向位移为x2、y2。则气流激振力作用下系统的运动微分方程为：

(7)

进行无量纲化后得到系统运动微分方程为：

(8)

τ=ωt、X1=x1/b、Y1=y1/b、X2=x2/b、

2数值计算及分析

由于非线性油膜力、汽轮机非线性间隙气流激振力的存在，方程具有强非线性特性，本文利用四阶Runge-Kutta方法对方程进行数值计算。本文转子轴承系统的主要参数为[13]：m1=4.0 kg，m2=32.1 kg，R=25 mm，L=12 mm，μ=0.018 pa·s，c1=1 050 N·s/m、c2=2 100 N·s/m、k=2.5×106N/m，e=0.05 mm，b=0.11 mm，气流激振力的参数选取为[18-19]：ρ0=11.8 kg/m3，RT=0.5 m，RB=0.37 m，β1=35°，β2=40°，ζ=0.83，δ=1.2×10-3m，V=200 m/s。系统一阶临界转速为ω0=882.5 rad/s。

2.1非线性间隙激振力对转子振动的影响

图4(a)和图4(b)分别为不考虑和考虑非线性汽流激振力作用时，转子系统随转速ω变化的分岔特性。图4(a)为不考虑非线性间隙气流激振力时，转盘随转速增大的响应分岔图。从图4(a)可以看出，随着系统转速ω的增大，在非稳态油膜力和转子离心力作用下，随着转速的增加逐渐表现出不同的非线性特征，系统先后经历了周期1运动、短暂的混沌、周期2运动、周期4运动、周期8运动、两个吸引子的混沌运动、周期8运动、周期4运动、周期2运动、周期5运动、高速域的拟周期复杂运动等形式。在转速较低时，系统处于稳定的周期1运动状态。随着转速的增大，由于非线性油膜力和离心力的共同作用，系统在ω=629 rad/s时出现倍周期分岔发生失稳，进而系统经倍周期分岔进入混沌运动，在ω=800 rad/s时经过倒分岔离开混沌运动，并在ω=1 496 rad/s进入超临界转速域的拟周期复杂运动状态。

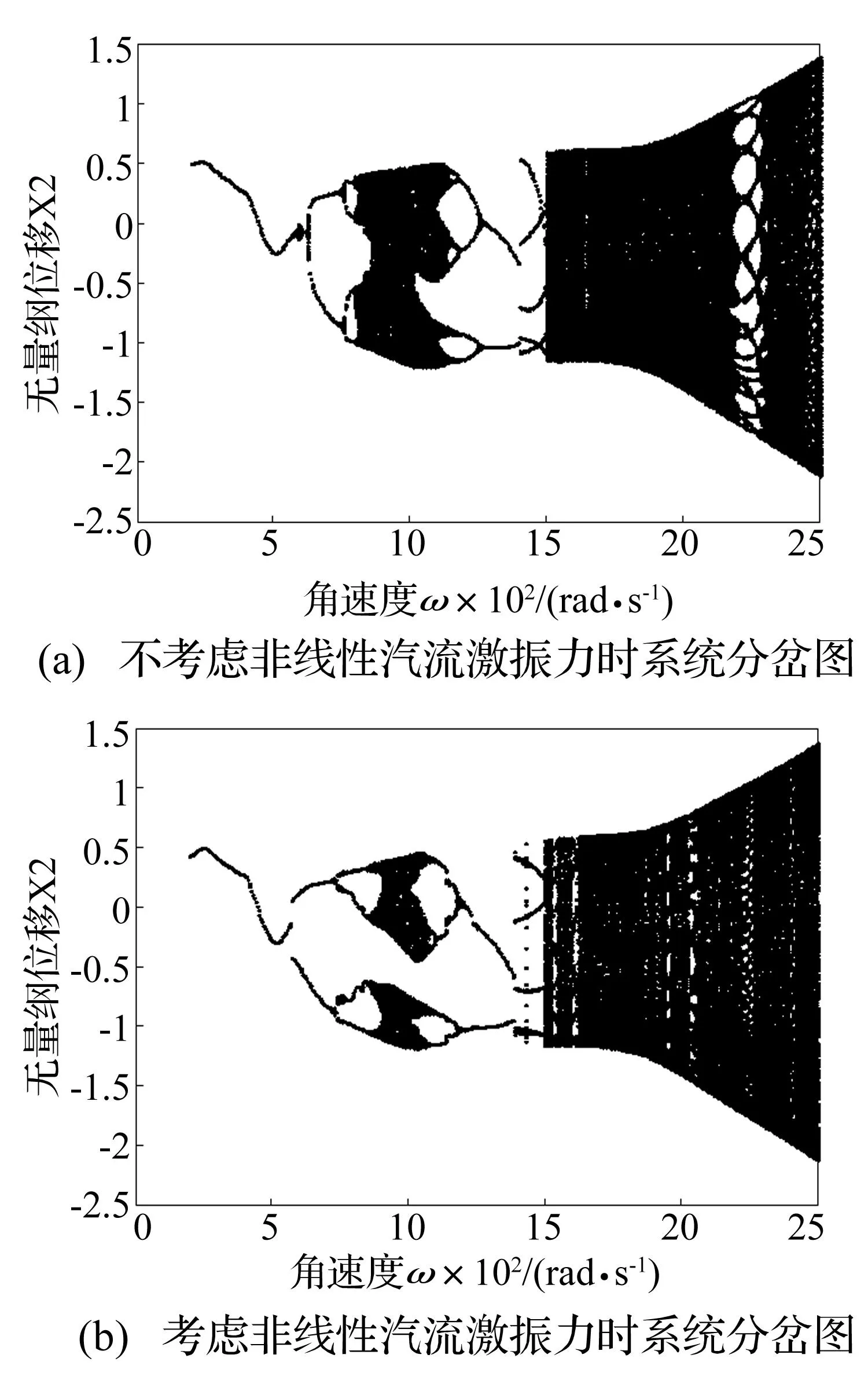
图4　转子系统随角速度ω变化的分岔图Fig.4 The bifurcation diagram of the rotor under the change of rotating speed

图5　不考虑激振力时的轴心轨迹图和Poincare映射图Fig.5 Portraits of central point of shaft and Poincare map of vibration response without the air-exciting force of Steam Turbine

图4(b)为考虑非线性间隙气流激振力作用时，转子系统随转速ω变化的分岔特性。图5和图6分别为不考虑和考虑汽轮机非线性间隙气流激振力作用时几个典型转速下的运动状态。对比图4(a)和图4(b)可以看出，不考虑非线性间隙气流激振力作用时在亚临界转速区域出现的短暂混沌消失，系统的周期性分岔有所提前且周期性分岔区域明显变长；并且在周期2与周期4之间出现周期7运动，如图6(a)所示在ω=755 rad/s时的轴心轨迹图和Poincare截面映射图，Poincare截面上表现为7个孤立的点。在临界转速附近，系统的混沌区域发生了明显的变化，系统响应为混沌运动的分岔图演变为两条压扁的自相似轨迹，且系统混沌区域明显减小；图6(b)所示转速为ω=955 rad/s时的轴心轨迹图和Poincare截面映射图，对比图5(a)可以看出，由于非线性间隙气流激振力的作用，轴心轨迹的形状发生了较大的变化，Poincare截面图由一个混沌岛状演变为两个孤立的岛状。在超临界转速区域，转子系统的拟周期运动有所延后，如图6(c)为转速ω=1 497 rad/s时的轴心轨迹图和Poincare截面映射图，对比图5(b)可以看出系统的响应在非线性间隙气流激振力作用下由拟周期运动演变为周期5运动。在高转速区域，转子偏心力及气流激振力明显增大，造成转子的横向振幅变大，图4可以看出在ω=2 500 rad/s附近转子的振幅超过了δ发生动静碰摩，这将会进一步加剧了转子的异常振动，造成系统的失稳。汽轮机非线性间隙气流激振力对转子运动产生这样的影响主要是由于非线性间隙气流激振力的存在增强了转子偏心的作用，从而改变了转子系统的动力学特性。

综上所述，可以看出：由于汽轮机非线性间隙气流激振力的作用，在亚临界转速区域出现的短暂混沌消失，系统的周期性分岔有所提前且周期性分岔区域明显变长，并且在周期2与周期4之间出现周期7运动；在临界转速区域附近，系统的混沌区域发生了明显的变化，系统响应为混沌运动的分岔图演变为两条压扁的自相似轨迹，且混沌区域减小；在超临界转速区域，转子系统的拟周期运动有所延后，使得系统的动力学特性发生了复杂的变化。

2.2裂纹深度对转子振动的影响

由于裂纹深度的不同，对转子系统的非线性振动会产生不同的影响。图7分析研究了在汽轮机非线性间隙激振力作用下，在不同裂纹深度对转子轴承系统响应过程的影响。随着裂纹深度的增加， 转子的振动

响应出现一系列的变化。由图7可以看出，在转速较小时，裂纹深度对系统的影响不大，而转速610 rad/s≤ω≤1 900 rad/s裂纹深度对系统的影响比较大。

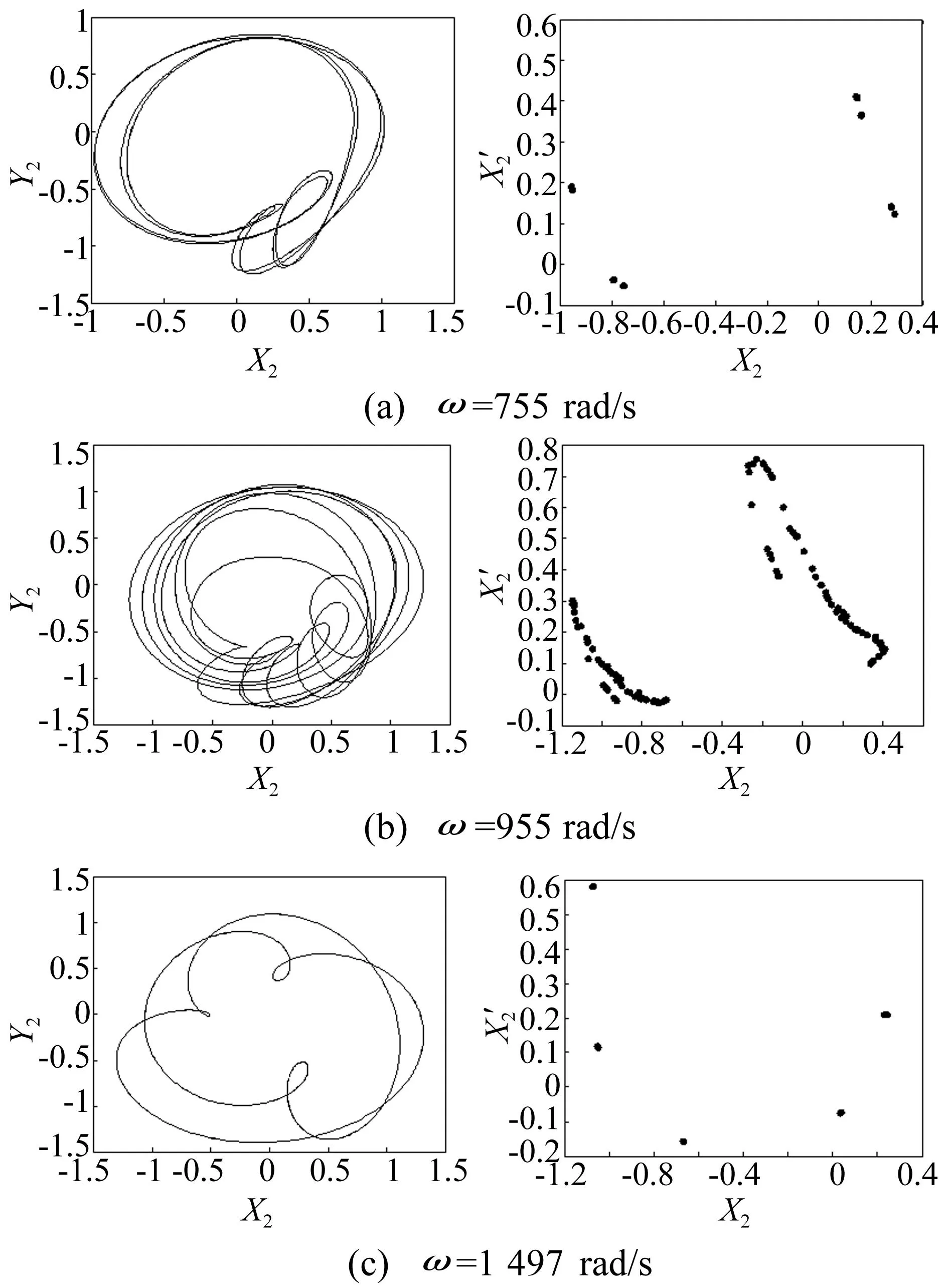
图6　考虑激振力时的轴心轨迹图和Poincare映射图Fig.6 Portraits of central point of shaft and Poincare map of vibration response with the air-exciting force of Steam Turbine

图7　不同裂纹深度时转子随转速ω变化的分岔图Fig.7 Bifurcation diagram of response of rotor under the change of rotating speed on different depths of crack

图8　不同裂纹深度下轴心轨迹图和Poincare截面图Fig.8 Portraits of central point of shaft and Poincare map of vibration response with the air-exciting force of Stream Turbine

图7(a)是转子在裂纹深度a/R=0.2时系统响应的分岔图，由于裂纹深度较小与图5(b)气流激振力作用下无裂纹转子的分岔图相比并没有明显的变化。当裂纹深度a/R=0.4时转子系统的分岔图与a/R=0.2时相比，并没有太大的变化，但是在临界转速附近的混沌区域变小，且在超临界转速区域出现周期8运动，如图8(a)所示。a/R=0.6时，由于裂纹深度增大和气流激振力耦合作用，系统在临界转速附近的混沌区域进一步缩小，可以看出在临界转速附近转子系统的分岔特征由两条近似对称的轨迹演变为四条自相似的轨迹，图8(b)为ω=995 rad/s时的轴心轨迹图和Poincare图，对比图6(b)可以看出由，由于裂纹深度的增大，Poincare映射图上两个混沌小岛演变为四个混沌小岛；对比图7(b)a/R=0.4时可以看出，出现周期5运动演变出周期8运动。随着裂纹深度进一步增大，当a/R=0.8时转子运动的混沌区域几乎消失，且在ω=995 rad/s处出现周期8运动，如图8(c)所示；在超临界转速区域，图8(d)为转速ω=1 530 rad/s时系统的轴心轨迹图和Poincare截面映射图，与图8(b)对比可以看出，由于裂纹深度的增大， 系统由周期8运动演变为周期11运动，在Poincare截面图上表现为11个孤立的点。当裂纹深度a/R=1.0时，由图7(e)可以看出，裂纹深度对亚临界转速、临界转速附近和超临界转速区域的复杂运动的影响都非常明显：亚临界转速区域的周期2运动几近消失；临界转速附近的混沌运动完全消失，且出现倒分岔现象；超临界转速区域，与裂纹深度较小时相比，周期运动消失，出现混沌区域，且在1 555 rad/s≤ω≤1 895 rad/s范围内出现较长周期3运动，如图8(e)所示为转速ω=1 665 rad/s时的轴心轨迹Poincare截面映射图。这主要是由于气流激振力和油膜力耦合作用造成的。从图4、5和图6、7可以看出：在汽轮机非线性间隙气流激振力、油膜力以及不平衡离心力的作用下，在浅裂纹时，汽轮机非线性间隙气流激振力对系统起主导作用，且在超临界转速区域出现周期8运动，随着裂纹深度的增加，系统运动的混沌区域逐渐减小直至消失，在超临界转速区域的逆周期运动演变为较长的周期3运动。产生这些复杂运动主要是由于转子系统随着裂纹深度的增大，转轴刚度不断变化，呈现出不同的非线性特征。这些非线性响应特征可以作为含裂纹转子在汽轮机非线性间隙气流激振力作用下耦合故障发生的典型特征，也可作为此类耦合故障诊断的依据。

3结论

针对在汽轮机非线性间隙气流激振力对转子系统影响研究中存在的不足，本文建立了在汽轮机非线性间隙气流激振力作用下，综合考虑非线性油膜力和不平衡离心力且具有弹性支承的裂纹转子-轴承系统的动力学模型，推导了系统的无量纲运动方程。采用数值积分方法对汽轮机转子的非线性动力学分岔特性做了较深入的研究。结果表明：

(1) 考虑汽轮机非线性间隙气流激振力作用时，在亚临界转速区域出现的短暂混沌消失，系统的周期性分岔有所提前且周期性分岔区域明显变长；在临界转速附近，系统响应为混沌运动的分岔图演变为两条压扁的自相似轨迹，且系统混沌区域明显减小；在超临界转速区域，由于气流激振力的作用，部分拟周期运动演变为周期5运动，转子系统的拟周期运动有所延后。在高转速区域，转子偏心力及气流激振力明显增大，造成转子的横向振幅变大，将会发生动静碰摩，进一步加剧了转子的异常振动，造成系统的失稳。

(2) 在浅裂纹时，汽轮机非线性间隙气流激振力对系统的响应起主导作用，且在超临界转速区域出现周期8运动；随着裂纹深度的增加，系统运动的混沌区域逐渐减小几乎消失，在超临界转速区域的逆周期运动演变为较长的周期3运动。随着裂纹深度的增加，裂纹对转子系统的影响也逐渐的明显和复杂。

(3) 研究结果揭示了在汽轮机非线性间隙气流激振力作用下含裂纹转子系统中的复杂非线性动力学现象，这些非线性响应特征可作为此类耦合故障诊断的依据。

参 考 文 献

[ 1 ] 赵常兴.汽轮机组技术手册[M].北京：中国电力出版社，2007.

[ 2 ] 黄文虎，夏送波，等.旋转机械非线性动力学设计基础理论与方法[M].北京：科学出版社，2006.12.

[ 3 ] Meng Guang，Hahn E J．Dynamic response of a cracked rotor with some comments on crack detection[J]．Journal of Engineering for Gas Turbines and Power,1 997，119(2)：447-455．

[ 4 ] Zou J，Chen J，Pu Y R. On the wavelet time-frequency analysis algorithm in identification of a cracked rotor[J]．Journal of Strain Analysis for Engineering Design，2002，37(3)：239-246．

[ 5 ] 李振平，金志浩，徐培民，等．含横向裂纹的弹性转子-轴承系统的动力学研究[J]．振动工程学报，2003，16(4)：468-471．

LI Zhen-ping,JIN Zhi-hao,XU Pei-min,et al. Dynamic study on elastic rotor-bearing system with a transverse crack[J].Journal of Vibration Engineering,2003,37(3):239-246.

[ 6 ] 张靖，闻邦椿．考虑摆振的裂纹转子的振动分析[J]．振动与冲击，2005，24(3)：9-11．

ZHANG Jing,WEN Bang-chun. Analysis on swing vibration of cracked rotor [J].Journal of Vibration and Shock, 2005,24(3):9-11.

[ 7 ] 于涛，孙伟，韩清凯．双裂纹转子系统非线性动力学特性研究[J]．振动与冲击，2013，32(19)：144-152．

YU Tao, SUN Wei, HAN Qing-kai. Nonlinear dynamic behavior of a dual-crack rotor system [J]. Journal of Vibration and Shock, 2013，32(19)：144-152.

[ 8 ] Sinou J J，Lees A W．A non-linear study of a cracked rotor[J]．European Journal of Mechanics ASolids，2007，26(1)：152-170．

[ 9 ] 朱厚军，赵玫，王德洋．Jeffcott裂纹转子动力特性的研究[J]．振动与冲击，2001，20(1)：1-4．

ZHU Hou-jun,ZHAO Mei,WANG De-yang. A study on the dynamic of a cracked Jeffcott rotor[J].Journal of Vibration and Shock,2001，20(1)：1-4.

[10] 郑吉兵，孟光．考虑非线性涡动时裂纹转子的分叉与混沌特性[J]．振动工程学报，1997，10(2)：190-197．

ZHENG Ji-bing,MENG Guang. The nonlinear influences of whirl speed on bifurcation and chaos of a cracked rotor[J].Journal of Vibration Engineering,1997,10(2):190-197.

[11] 于海，陈予恕，曹庆杰．多自由度裂纹转子系统非线性动力学特性分析[J]．振动与冲击，2014，33(7)：92-98．

YU Hai, CHEN Yu-shu, CAO Qing-jie. Nonlinear dynamic behavior analysis for a cracked multi-DOF rotor system [J]. Journal of Vibration and Shock,2014，33(7)：92-98.

[12] 岳二团，甘春标，杨世锡．气息偏心下永磁电机转子系统的振动特性分析[J]．振动与冲击，2014，33(8)：29-34．

YUE Er-tuan, GAN Chun-biao, YANG Shi-xi. Vibration characteristics analysis of a rotor for a permanent magent motor with Air-Gap Eccentricity [J]. Journal of Sound and Vibration , 2014，33(8)：29-34.

[13] 黄志伟，周建中，贺徽，等．不平衡磁拉力作用下裂纹转子系统的分岔[J]．机械工程学报，2011，47(13)：59-64．

HUANG Zhi-wei, ZHOU Jian-zhong, HE Hui,et al. Bifurcation of a cracked rotor-bearing system under unbalanced magnetic pull [J]. Journal of Mechanical Engineering, 2011,47(13):59-64.

[14] Sinou J J. Effects of a crack on the stability of a non-linear rotor system[J]. International Journal of Non-linear Mechanics,2007,42:959-972.

[15] 邹剑，董广明，陈进.含初始弯曲裂纹转子的振动分析[J].振动与冲击，2012,31(3):153-156.

ZOU Jian, DONG Guang-ming, CHEN Jin. Vibration analysis of cracked with initial deflection [J]. Journal of Vibration and Shock, 2012,31(3):153-156.

[16] Cao Jun-yi,Xue Shi-ming,Lin Jing.Nonlinear dynamic analysis of a cracked rotor-bearing system with fractional orderdamping[J].Journal of Computational and Nonlinear Dynamic,2013.7.031008:1-14.

[17] Guo Chao-zhong, Mohammad A. Shudeifat A L,et al. Stability analysis for transverse breathing cracks in rotor systems[J], European Journal of Mechanics A/Solids. 42(2013)27-34.

[18] 柴山，张耀明，赵又群，等.汽轮机非线性间隙气流激振力分析(Ⅰ)——相对进气速度沿叶高不变[J].非线性动力学学报，2000，7(1)：25-32.

CHAI Shan, ZHANG Yao-ming, ZHAO You-qun,et al. An analysis on the non-linear air exciting-vibration force caused by clearance[J]. Journal of Nonlinear Dynamic in Science and Technology,2000,7(1):25-32.

[19] 柴山，张耀明，曲庆文，等.汽轮机间隙气流激振力分析 [J].中国工程科学，2001，3(4)：68-72.

CHAI Shan, ZHAO Yao-ming, QU Qing-wen,et al. The analysis on the air-exciting-vibration force of steam turbine[J]. Engineering Science,2001,3(4):68-72.

[20] 柴山，刚宪约，张耀明，等.汽轮机间隙气流激振力分析及计算程序设计[J].山东工程学院学报，2000，14(3)：1-5.

CHAI Shan, GANG Xian-yue, ZHANG Yao-ming,et al. Analysis of the air-exciting-vibration force of the steam turbine and its computer and its computer program designing[J]. Journal of Shandong Institute of Technology, 2000,14(3):1-5.

[21] Li Ru-qiang,LIU Yuan-feng. Simulation of crack diagnosis of rotor based on multi-scale singular-spectrum analysis[J].Chinese Journal of Mechanical Engineering,2006,19(2):282-285.

[22] 曾复，吴昭同，严拱标.裂纹转子的分岔与混沌特性分析[J].振动与冲击，2000，19(1)：40-42.

ZENG Fu, WU Zhao-tong, YAN Gong-biao. Analysis of bifurcation and chaos on a cracked rotor[J].Journal of Vibration and Shock, 2000,19(1):40-42.

[23] Adileftta G,Guido A R,Rossi C. Chaos motions of a rigid rotor in the short journal bearings[J].Nonlinear Dynamics,1996,10(3):251-269.

Bifurcation characteristic of a cracked rotor-bearing system under air-exciting forces of steam turbine

WENGLei1,2,YANGZi-chun1,2,CAOYue-yun1,2(1. Institute of High Temperature Structural Composite Materials for Naval Ship，Naval University of Engineering，Wuhan 430033, China; 2. College of Power Engineering, Naval University of Engineering, Wuhan 430033, China)

Abstract:The dynamic model of a cracked rotor-bearing system under air-exciting forces of steam turbine was established. Numerical method was adopted to analyze bifurcation and chaos characteristics of the system. The effects of air-exciting forces of steam turbine and depths of crack on the vibration response of the rotor were discussed using Poincare’s cross-section, portraits of central point and bifurcation diagrams. The results indicated that the dynamic periodic responses of the system occur in advance and its chaotic motion region decreases due to air-exciting forces of stream turbine; moreover, for the dynamic responses of the system, the air-exciting forces of stream turbine play a dominant role in case of shallow cracks, and period-eight motions appear in the super-critical speed region of the system; with increase in crack depth, the system’s chaotic motion region decreases and almost disappears around the critical speed; the system’s quasi-period motions become a longer period-three motion in the system’s super-critical speed region. The study results provided a reference for further understanding the failure mechanism of such a rotor-bearing system.

Key words:bifurcation; rotor-bearing system; air-exciting forces of steam turbine; nonlinear vibration

中图分类号:TB561；U661.42

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.05.014

通信作者杨自春 男，教授，博士生导师，1967年生

收稿日期：2015-03-09修改稿收到日期：2015-09-18

基金项目：海军十二五预研基金(010502010261002)

第一作者 瓮雷 男，博士生，1988年生