边界条件对有限长正方形棱柱气动力的影响

王汉封, 杨　帆, 邹　超(.中南大学 土木工程学院，长沙　40075； 2.高速铁路建造技术国家工程实验室，长沙　40075)



边界条件对有限长正方形棱柱气动力的影响

王汉封1，2, 杨帆1, 邹超1(1.中南大学 土木工程学院，长沙410075； 2.高速铁路建造技术国家工程实验室，长沙410075)

摘要：通过风洞实验研究了均匀流与湍流边界层中一端固定于壁面、另一端为自由端的有限长正方形棱柱气动力特性。实验模型宽度d = 200 mm，高宽比H/d = 5。基于自由流风速U(∞)与d的雷诺数Red = 0.68×105～5.47 × 105。研究发现，均匀流与湍流边界内有限长正方形柱气动力均不存在明显的雷诺数效应。棱柱局部时均阻力系数、脉动阻力系数和脉动升力系数沿展向存在明显差异。湍流边界层会增大与。且均匀流中脉动风压与气动力的双稳态现象在湍流边界层内基本消失。经POD分析，确定了对称与反对称等两种典型风压分布状态对脉动风压的贡献率。均匀流中，柱体两端附近风压脉动由对称或准对称风压分布所控制；而柱体中部则由反对称风压分布控制。湍流边界层中所有高度风压脉动均由反对称风压分布控制。两种边界条件下，仅反对称形态的POD模态具有明显周期性并对柱体气动力周期性起支配作用。尽管对称风压POD模态在某些位置占支配地位，但其无明显周期性。

关键词：有限长棱柱;气动力;边界层条件;双稳态;POD

高耸结构在工程中广泛存在，如高层建筑、烟囱、冷却塔等。在自由端与壁面边界层的共同作用下，此类一端固定于壁面、另一端为自由端的三维钝体绕流与二维钝体绕流存在显著差异。研究表明，三维钝体尾流中除展向涡外，自由端后会存在强烈的下扫流，并伴随有一对流向拖拽涡，即顶部涡[1-3]。此外，如果壁面边界层厚度较大，会在有限长钝体底部形成上升流，且伴随一对与顶部涡旋向相反的底部涡[4]。上述展向涡、顶部涡与底部涡的相互作用，使得三维钝体尾流中的展向涡脱落具有显著的三维性与间歇性[2,6]。

通常认为有限长正方柱棱柱的尾流特性与其高宽比(H/d)有关[3,6]，当H/d小于临界值，展向涡将由反对称的Karman涡街形式转化为对称形式。对处于均匀来流中的H/d=3、5、7的有限长正方形棱柱尾流的研究发现，所有H/d棱柱尾流中都可以观察到反对称与对称形态的尾流结构。即使对于远大于临界值的H/d=7的方柱，其尾流中间高度上依然有超过10%的展向涡呈对称形态[4]。上述二种典型尾流结构的出现具有随机性与间歇性，势必给气动力带来影响。然而，现有研究大多关注三维柱体气动力的时均统计特性，对其瞬态特性较少涉及，对上述尾流中展向涡间歇性对气动力的影响机理尚没有清晰认识。

本征正交分解(Proper Orthogonal Decomposition, POD)是分析复杂随机场时空特性的重要工具。POD方法可将随机场分解为仅依赖时间的主坐标和仅依赖空间的本征模态，实现对随机现象的时空分离，有利于突出随机场的主要特性[7-8]。目前，POD已在很多领域得到了成功的应用[9-11]。Armitt[12]首先将POD方法应用于风工程领域，分析了冷却塔表面的风压特性。Best等[13-14]应用POD分析脉动压力场，指出结构风致均方根响应的计算可简化为前几阶本征模态的贡献。李方慧等[15-16]利用POD技术重建了屋盖风压场。邹垚[17]则利用修正的本征模态重建了风压场。肖志勇[18]推导了结构风致振动分析的双模态变换方法，应用POD方法进行了脉动风荷载及风振响应分析。

本文以H/d=5的正方形棱柱为对象，通过风洞实验测量均匀流与湍流大气边界层条件下方柱表面的瞬时风压。系统的研究了边界条件对有限长方形棱柱气动力的影响规律，并运用POD方法对脉动风压场进行了深入的研究，揭示了不同边界条件下气动力差异的机理。

1POD方法简介

POD原理的推导有多种途径, 例如可利用概率论的Karhunen-Loeve分解定理，也可从投影极值原理或拉格朗日乘子方法出发，还可以根据结构动力学的瑞利商概念推导。推导方式都是先引出特征值问题, 然后导出主坐标概念及其性质。由于本文中处理的数据集合点数较为庞大，直接求解特征问题，其求解过程会非常困难。故本文中运用的POD分析方法是由Sirovich提出的快照POD(Snapshot POD)算法[19]。在全部测量样本中任意选取连续的2 000个时刻的瞬时压力集合建立POD空间。首先将瞬时压力场分解为时均压力场和脉动压力场，即

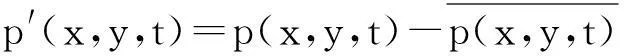
(1)

根据POD方法的基本思想，目标是将脉动量p′(x,y,t)作如下分解：

(2)

式中，x,y表示模型表面测点的位置坐标，t表示时间，an(t)为仅与时间有关的模态系数，φn(x,y)为仅与空间位置相关的风压POD模态。实际上，求φn(x,y)等价于求解以下最大值问题：

(3)

且满足：

(φ,φ)=‖φ‖2=1

(4)

同时利用原有函数空间快照脉动量的线性组合来表示空间模态，即：

(5)

利用变分法，结合式(3)和式(5)上述最大值问题转化为以下特征值问题：

(6)

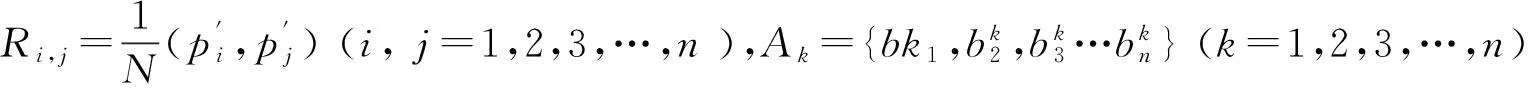
Φ=span(φ1,φ2,…，φn)

(7)

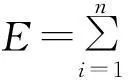
2实验方法

本实验在中南大学高速铁路建造技术国家工程实验室下属风洞实验室完成。该风洞为双实验段回流式风洞，其中低速试验段宽12 m、高3.5 m、长18 m，风速范围2～18 m/s，湍流度小于2%；高速试验段宽3 m、高3 m、长15 m，风速范围为5～90 m/s，湍流度小于0.5%。本文实验在该风洞高速试验段内进行。

实验中，正方形棱柱一端固定于风洞底面，另一端为自由端。图1给出了实验装置示意图与坐标系的定义。柱体宽度d=200 mm，高宽比H/d=5，模型造成的风洞阻塞度约为2.2%，其影响可以忽略不计。实验中自由来流风速U∞为5～40 m/s，对应雷诺数Red=0.68×105～5.47 ×105。自由流风速由置于边界层外，距离风洞上壁面约0.5 m的皮托管测量得到。为研究有限长柱体气动力的三维性，在柱体展向不同高度布置了四层压力测点，分别位于柱体底部附近、中间高度处和自由端附近，即z*= 1，2.5，4和4.5处(本文中上标‘*’表示用d或U∞无量纲化)。每层布置40个压力测点，其中迎风面16个，背风面与两个侧面各8个，如图1所示。对每层测点风压积分可获得对应高度上的局部气动力，将局部气动力沿展向积分(加权平均)可以估算有限长棱柱的总体气动力。实验中各测点用内径约0.6 mm、长度约30 cm的测压管与压力扫描阀连接。实验表明该长度测压管道阻尼对频率为35 Hz以下信号的影响可忽略[21]。本实验中大尺度涡脱落频率为7 Hz左右，因此后续分析中将忽略测压管阻尼影响。本实验使用的是Scanivalve公司DSM3400电子压力扫描阀系统。试验中每通道采样频率为625 Hz，各测点采样样本数为2万。

为提供对比参照，本实验还对均匀来流条件下的二维方柱表面风压进行了测量。二维方柱宽度与三维棱柱相同，并贯穿高速试验段。二维方柱实验风速范围5～20 m/s，对应雷诺数Red=0.68×105～2.74×105。压力测孔位于柱体展向中间截面，周向分布与三维棱柱相同。扫描阀测量参数设置也与三维棱柱风压测试实验相同。

为探讨边界条件对有限长方形棱柱气动力的影响规律，本文在均匀流与湍流边界层条件下进行了两组实验。值得强调的是，对于一端固定于壁面的悬臂棱柱而言，不存在严格意义上处于均匀流中的情况，因为壁面上始终有边界层存在。本文中的均匀流条件是指仅存在空风洞时壁面自然形成的边界层的情况；而湍流边界层是在风洞试验段内加装尖塔与粗糙元得以实现[22-23]。模型安装前，用眼镜蛇探针对均匀流与湍流边界层条件下的来流速度、湍流度进行了标定，如图2所示。由标定结果可知，空风洞壁面边界层厚度约为200 mm，即棱柱除底部约1d处于边界层内，绝大部分仍处于均匀来流中；而湍流边界层厚度约为1 400 mm，此时整个棱柱完全浸没于湍流边界层中。

图1　实验模型与坐标系定义示意图Fig.1 Experimental setup and definition of coordinates system

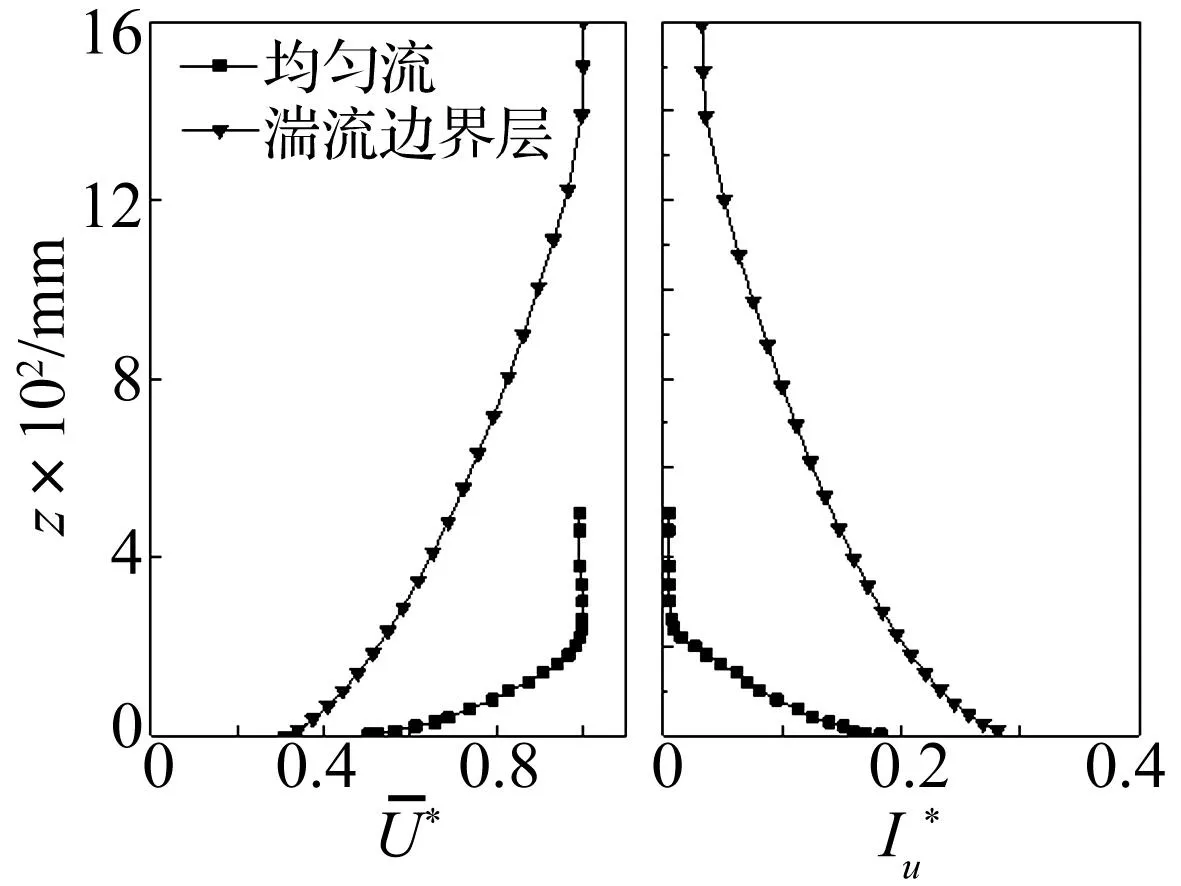
图2　两种实验来流条件Fig.2 Two tested oncoming flow conditions

3结果与讨论

3.1气动力特性

图3　总体阻力系数与局部阻力系数Fig.3 Total drag coefficient and local drag coefficient

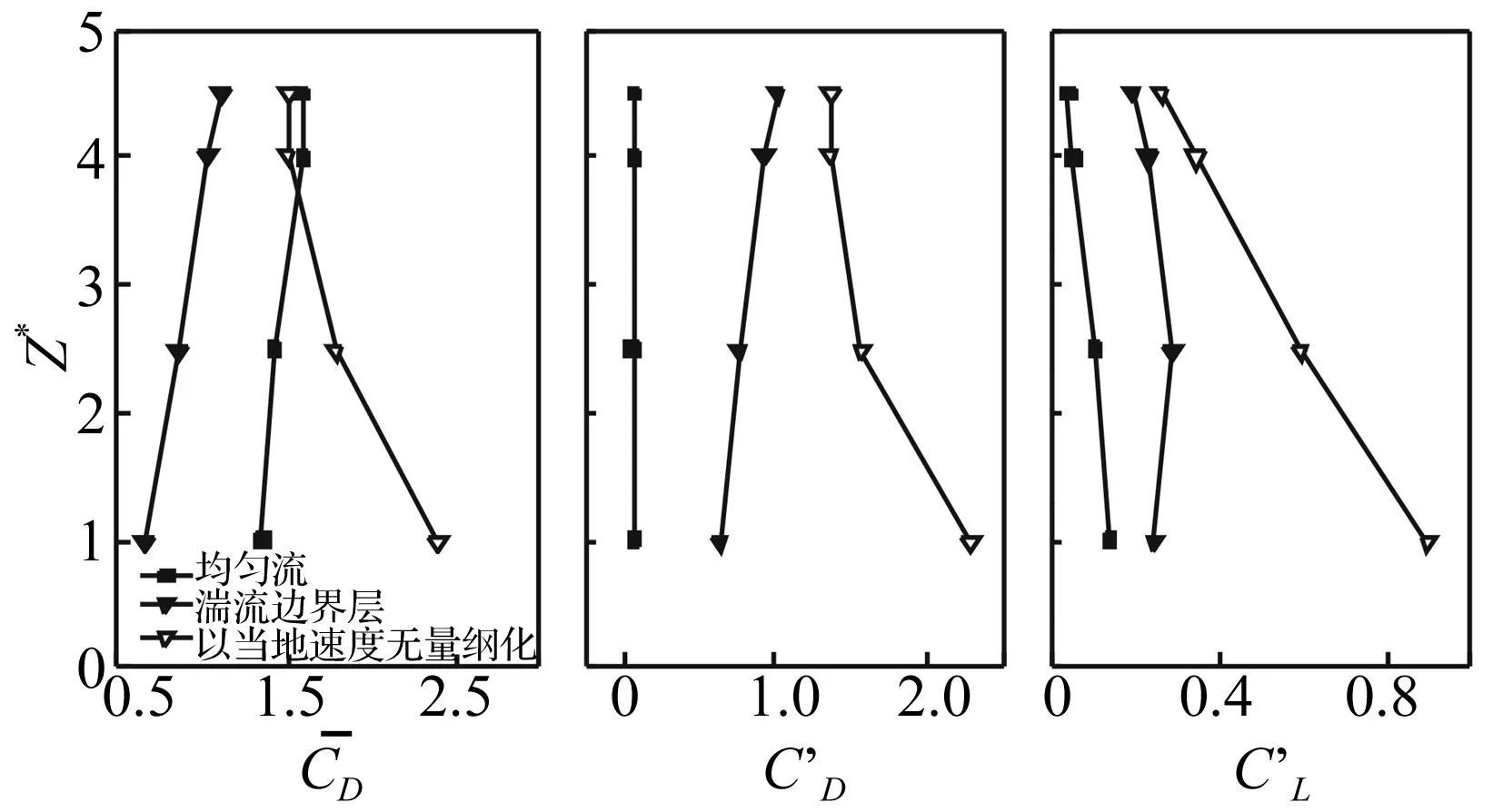
图4　局部气动力参数 Fig.4 Local aerodynamic forces

图5　柱体表面与Cp_rms分布Fig.5 Distribution of and Cp_rms

与均匀流中结果相反，在湍流边界层中迎风面风压随z*有显著变化(如图5(c)示)，这显然是由于来流风速随高度增加而增加所造成的。此外，相对于均匀流中的结果，湍流边界层中棱柱不同高度上的背风面风压较为均匀。对比不同边界条件下的Cp_rms可以发现，湍流边界层的存在使得棱柱表面风压脉动明显加强。尤其是柱体侧面B、D的脉动风压基本是均匀流中的两倍。而且，在湍流边界层中柱体下半部分的Cp_rms值相对较大，这可能意味着湍流边界层中展向涡强度要明显大于均匀流，且越接近地面展向涡强度越大。

图6给出了柱体中间高度z*= 2.5处左、右两侧面中点的瞬时压力信号Cp_l和Cp_r。可以发现不同边界条件下的风压瞬时信号具有如下区别：首先，均匀流中风压波动幅度(图6(a))远小于湍流边界层中的对应值(图6(b))；其次，在均匀流中风压大幅周期性波动并非始终存在，而是间歇性出现的。当周期性波动出现时，Cp_l和Cp_r相位相反；而当周期性波动不存在时，两者无明显相位关系。而湍流边界层内风压始终存在明显的周期性波动，且Cp_l和Cp_r相位相反。这表明湍流边界层内的脉动升力将远大于均匀流中对应值，与图4所示结果一致。

图6(c)～(d)与图6(e)～(f)给出了对应的升力系数和阻力系数。可以看出当Cp_l和Cp_r出现大幅周期性波动时，对应的CL和CD也会大幅波动。在均匀流中，风压与CL出现大幅周期性波动时，对应的CD相对较大；反之CD相对较小。

图7给出了均匀流和边界层条件下不同高度上两侧面中点瞬时风压的功率谱。为方便比较，各功率谱均用其最大值无量化为分贝(dB)。两种来流条件下，风压功率谱中都存在明显的峰值，且越靠近自由端峰值越小。这表明越靠近自由端，风压周期性越弱。这是因为自由端附近的下扫流削弱了柱体上半部分的展向涡，而其对柱体下半部分的影响较小。湍流边界层中风压的斯托劳哈数St为0.074，明显小于均匀流中对应值0.104，且两者均明显小于二维方柱对应值0.12～0.13[26-27]。值得注意的是，虽然在湍流边界层内不同高度的来流速度并不相同，但所有高度的St数却完全相同。这说明在均匀来流和湍流边界层中，有限长柱体尾流都仍是一个整体。此外，湍流边界层内功率谱的尖峰比均匀流中更宽，尤其是z*= 1处这一现象更为明显，显然是因为湍流边界层内柱体展向涡脱更为复杂所造成的。

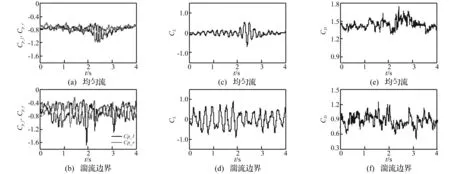
图6　方柱中间高度瞬时CP, CL 与CDFig. 6 Instantaneous Cp, CL and CD at cylinder mid-span

图7　柱体中间高度脉动风压功率谱Fig.7 Spectra of the fluctuation pressure at cylinder mid-span

3.2POD分析

图8、图9分别给出了不同边界条件下柱体不同高度上风压的前三阶POD模态，其中图8还给出了二维方柱的对应结果以供对比。表1给出了各主要POD模态对风压脉动的贡献率。由于各模态中风压分布随模态数的增加而逐渐变得不规则，且其对脉动风压的贡献也迅速减小，因此本文中将仅讨论风压分布物理意义清晰的前几阶模态。

图8　均匀流中不同高度前三阶POD模态压力分布图Fig.8 The first three POD modes of fluctuation pressure in uniform flow

对于二维方柱，模态1对应的风压分布为反对称形态，显然是由交替脱落的展向涡所造成的[27]。由表1可知，模态1对风压脉动的贡献率达到82.7%，由此可知，二维方柱的气动力主要由交替脱落的展向涡所对应的模态1所控制。如图8所示，二维方柱的模态2也反呈反对称分布。由此可知，对应着反对称风压分布的模态1和模态2对于二维方柱风压脉动的贡献率达到88.2%(82.7+5.5)，占据了绝对主导地位。二维方柱的模态3中两侧面风压为对称状态，但其仅贡献了风压脉动的3.9%。

图9　湍流边界层中不同高度前三阶POD模态压力分布图Fig.9 The first three POD modes of fluctuation pressure in turbulent boundary layer

工况模态1模态2模态3模态4二维方柱82.7%5.5%3.9%2.9%z*=4.580.4%7.0%3.2%1.1%均匀流z*=450.1%15.7%8.7%3.9%z*=2.542.7%26.2%9.3%4.9%z*=149.9%27.9%7.4%2.5%z*=4.536.9%20.8%11.3%8.0%湍流边界层z*=437.9%24.9%10.8%4.6%z*=2.551.3%10.9%8.8%6.8%z*=143.9%11.7%8.7%8.0%

均匀流中有限长柱体的风压模态及其对应贡献率在不同高度上有明显差异。首先，柱体两端附近z*=4.5，4和1处，模态1为对称或准对称形态，且其对应贡献率分别为80.4%，50.1%和49.9%；而柱体中间高度z*=2.5处，模态1为反对称形态，类似于二维方柱结果，但其贡献率仅为42.7%。其次，柱体两端附近z*=4.5，4和1处的模态2都呈现了反对称形态，对应贡献率为7.0%，15.7%和26.2%。与此相反，柱体中间高度的模态2为准对称形态，贡献率为26.2%。由上述分析可知，在均匀流中有限长方形柱体两端附近的风压脉动是由对称(或准对称)形态占主导的；尽管在柱体中间高度处，反对称风压分布占据了主导地位，但其贡献率仅为42.7%，远低于二维方柱对应值(82.7%)。总的来看，对称与反对称形态的风压脉动在所有高度上都存在，其中柱体中间部分以反对称形态为主；而柱体两端，尤其是自由端附近，则是对称形态风压分布占主导地位。这说明自由端所产生的下扫流具有抑制反对称展向涡，而将其转化为对称形态的趋势。

湍流边界层内，柱体表面风压的POD分析结果表现出与均匀流中完全不同的规律。如图9所示，所有高度上模态1都对应了反对称的风压分布，而模态2都对应了对称或准对称的风压分布。反对称模态1的贡献率在柱体中间高度z*=2.5处最大，达到51.3%。靠近柱体两端，反对称风压分布的贡献逐渐小，尤其是自由端附近减小的更为显著，这与均匀流中的规律是类似的。各高度的模态2都表现为对称或准对称分布，但其贡献率远小于均匀流中对称风压分布的贡献率(见表1)。

对比图8、图9与表1中各模态贡献率可知，均匀来流中柱体自由端和底部附近的风压脉动由对称或准对称风压形态控制，而中间高度处则由反对称风压形态控制，这与文献[6]中流场的测量结果是一致的。湍流边界层内柱体所有高度上的风压脉动都是由反对称形态控制，且柱体中间高度上反对称的模态1贡献率最大，接近两端(尤其是自由端)，反对称形态贡献率较小，但都明显大于均匀流中反对称形态的贡献率。这一现象表明湍流边界层有将展向涡从对称形态转化为反对称形态的趋势。这可能是因为，对称形态展向涡本身是一种不稳定的形态[29]，湍流边界层内的扰动将抑制这种不稳定的对称展向涡的产生。

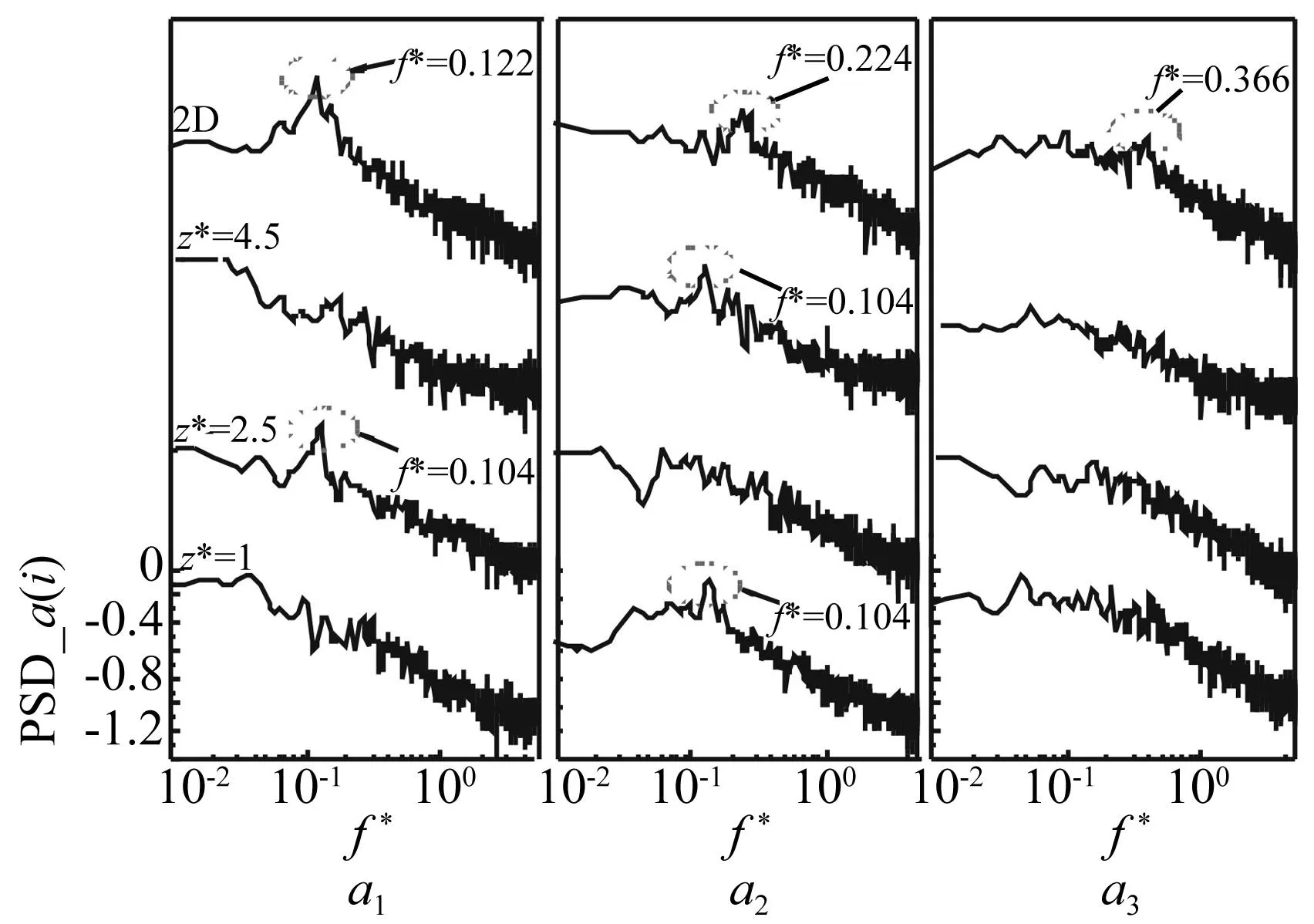
图10　均匀流中风压POD系数功率谱Fig. 10 Spectra of the coefficients of POD modes inuniform flow

图11　湍流边界层中风压POD系数功率谱Fig.11 Spectra of the coefficients of POD modes in turbulent boundary layer

POD主坐标an(t)反映了各模态对瞬时风压分布贡献随时间的变化情况。图10、图11给出了均匀流与湍流边界层中POD前三阶模态主坐标的功率谱。如图10所示，二维方柱模态1主坐标a1功率谱具有强烈峰值，且对应无量纲支配频率为0.122，与其St数吻合。其模态2主坐标a2功率谱同样具有明显峰值，且对应无量纲支配频率为0.244，约为2倍St。而代表对称风压分布的模态3主坐标a3谱的峰值相对较弱，其对应支配频率为0.366,约等于3倍St。这些POD主坐标谱峰值所对应的支配频率与图7所示二维方柱风压功率谱中的主频率及其二阶、三阶谐波频率相吻合。

均匀流中，z*=2.5时模态1功率谱出现强烈峰值，对应支配频率为0.104，与瞬时风压St数吻合。而该高度上代表对称风压分布的模态2和模态3均无明显周期性。靠近柱体两端z*=1和4.5时，一阶模态代表了对称或准对称风压分布(如图8示)，而其系数a1谱并无明显峰值，如图10示。然而，z*=1和4.5处代表着反对称风压分布的模态2系数谱却存在着显著的峰值，且其对应的支配频率也为0.104，与z*=2.5是模态1相同。由此可知，尽管反对称风压分布在柱体两端附近并不占主导地位，但其仍具有明显的周期性；而对称风压分布尽管在风压脉动中贡献较大，但其却无显著周期性。

湍流边界层内，不同高度上模态1主坐标功率谱均出现有强烈峰值，且其对应频率都是0.074，与图7所示风压St数吻合。然而，此时代表着对称或准对称风压分布的模态2，尽管其对风压贡献率依然较大(表1)，但其功率谱已无明显周期性。对比图10，11与图8，9可以发现，只要是压力分布呈现反对称的POD模态，其主坐标系数都具有很强的周期性。反之，压力分布呈对称或准对称形态的POD模态，其系数则无明显的周期性。

4结论

通过风洞实验研究了均匀来流与湍流边界中的H/d=5方柱表面风压与气动力特性，利用POD方法分析了其风压脉动，主要结论如下：

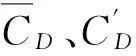
(3) 脉动风压的POD分析发现，均匀流中仅柱体中间高度被反对称的一阶模态控制，但其贡献率远低于二维方柱对应值。柱体两端，尤其是自由端附近，风压脉动被对称形态的一阶模态控制，反对称的二阶模态贡献相对较小。而湍流边界层内，柱体所有高度上风压脉动都被反对称的一阶模态支配，这说明湍流边界层具有将对称展向涡转化为反对称展向涡的趋势。无论是均匀流或是湍流边界层内，反对称风压分布模态具有明显的周期性；而对称或准对称风压分布模态无明显周期性。

参 考 文 献

[ 1 ] Summer D. Flow above the free end of a surface-mounted finite-height circular cylinder: a review [J]. Journal of Fluids and Structures, 2013, 43: 41-63.

[ 2 ] Park C W, Lee S J. Free end effects on the near wake flow structure behind a finite circular cylinder [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2000, 88: 231-246.

[ 3 ] Summer D, Heseltine J L, Dansereau O J P. Wake structure of a finite circular cylinder of small aspect ratio [J]. Experiments in Fluids, 2004, 37: 720-730.

[ 4 ] Wang H F, Zhou Y, Chan C K,et al. Effect of initial conditions on interaction between a boundary layer and a wall-mounted finite-length-cylinder wake [J]. Physics of Fluids, 2006, 18: 065-106.

[ 6 ] Wang H F, Zhou Y. The finite-length square cylinder near wake [J]. Journal of Fluid Mechanics, 2009, 638: 453-490.

[ 7 ] Tamura Y, Suganuma S, Kikuchi H et al. Proper orthogonal decomposition of random wind pressure field [J]. Journal of Fluids and Structures, 1999, 13: 1069-1095.

[ 8 ] 谢龙，靳思宇，王玉璋，等． 阀体后90°圆形弯管内部流场PIV测量及POD 分析 [J]． 实验流体力学，2012，26(3) ：21-25．

XIE Long, JIN Si-yu, WANG Yu-zhang, et al. PIV measurement and POD analysis of inner flow field in 90°bending duct of circular-section with fore-end valve [J]. Journal of Experiments in Fluid Mechanics, 2012, 26(3) ：21-25．

[ 9 ] 阳祥，丁鹏，李增耀，等．基于POD 方法的湍流大尺度信息提取与分析 [J]．工程热物理学报，2010，30(6)：1019-1021．

YANG Xiang, DING Peng, LI Zeng-yao, et al. Extraction and analysis of turbulent large scales based on POD method [J]. Journal of Experiments in Fluid Mechanics, 2010, 30(6): 1019-1021．

[10] Bienkiewicz B. New tools in wind engineering [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1996, 65: 279-300.

[11] Slater J C, Pettit C L, Beran P S. In-situ residual tracking in reduced order modeling [J]. Shock and Vibration, 2002, 9: 105-121.

[12] Armitt J. Eigenvector analysis of pressure fluctuations on the west burton instrumented cooling tower [R]. Central Electricity Research Laboratories (UK), Internal Report RD/L/N, 1968: 114-168．

[13] Best R J, Holmes J D. Use of eigenvalues in the covariance integration method for determination of wind load effects [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1983, 13: 359-370.

[14] Holmes J D, Best R J. An approach to the determination of wind load Effects on low-rise buildings [J].Journal of Wind Engineering and Industrial Aerodynamics, 1981, 7: 273-287.

[15] 李方慧，倪振华，谢壮宁. POD方法在重建双坡屋盖风压场中的应用[J]. 工程力学，2005，22(增刊1)：177-182.

LI Fang-hui, NI Zhen-hua, XIE Zhuang-ning. Application of POD to reconstruction of wind pressure fields on pitched roof [J]. Engineering Mechanics, 2005, 22(Sup1): 177-182.

[16] 李方慧，倪振华，沈世钊．POD 原理解析及在结构风工程中的几点应用 [J]．振动与冲击，2009，28(4)：29-33．

LI Fang-hui, NI Zhen-hua, SHEN Shi-zhao. Theory of POD and its application in wind engineering of structures [J]. Journal of Vibration and Shock, 2009, 28(4):29-33.

[17] 邹垚，梁枢果，邹良浩． 基于本征模态修正的POD法在风场重建中的应用 [J]．土木工程学报，2010，43：305-309．

ZOU Yao, LIANG Shu-guo, ZOU Liang-hao. Reconstruction of fluctuating wind pressure field by applying POD of eigenvector correction [J]. China Civil Engineering Journal, 2010, 43: 305-309．

[18] 肖智勇. 本征正交分解POD方法在高层建筑风荷载及其动态相应中的应用研究[D].汕头:汕头大学,2001.

[19] Sirovich L. Turbulence and the dynamics of coherent structures [J]. Quarterly of Applied Mathematics, 1987, 45: 561-590.

[20] Ben Chiekh M，Michard M，Guellouz M S，et al． POD analysis of momentumless trailing edge wake using synthetic jet actuation [J]．Experimental Thermal and Fluid Science, 2012, 46: 89-102.

[21] 杨艳静，陈青松，蔡峰，等. 管道测压系统频率响应研究 [J].实验流体力学，2006，20(2)：85-89.

YANG Yan-jing, CHEN Qing-song, CAI Feng, et al. Research on frequency response of tube pressure measurement system [J]. Journal of Experiments in Fluid Mechanics, 2006,20(2): 85-89.

[22] 黄鹏，全涌，顾明. TJ-2风洞大气边界层被动模拟方法的研究[J]. 同济大学学报，1999，27(2)：136-144.

HUANG Peng，QUAN Yong，GU Ming. Research of passive simulation method of atmospheric boundary layer in TJ-2 wind tunnel [J]. Journal of Tongji University，1999, 27(2): 136-144.

[23] 石碧青，洪海波，谢壮宁,等. 大气边界层风洞流场特性的模拟 [J] 空气动力学学报， 2007，25(3)：376-380.

SHI Bi-qing, HONG Hai-bo, XIE Zhuang-ning, et al. Wind tunnel simulation of atmospheric boundary layer [J]. Acta Aerodynamica Sinica, 2007, 25(3): 376-380.

[24] Lee B E. The effect of turbulence on the surface Pressure field of a square Prism [J]. Journal of Fluid Mechanics, 1975, 69: 263-282.

[25] 张卫国. 正多棱柱绕流特性实验研究 [D].北京：清华大学，2010.

[26] Okajima A. Strouhal numbers of rectangular cylinders [J]. Journal of Fluids Mechanics, 1982, 123: 379-398.

[27] Kawai H, Okuda Y, Ohashi M. Near wake structure behind a 3D square prism with the aspect ratio of 2.7 in a shallow boundary layer flow[C]//Journal of Wind Engineering and Industrial Aerodynamics, 2012, 104-106: 196-202.

[28] Van Oudheusden B W, Scarano F, Van Hinsberg N P, et al. Phase-resolved characterized of vortex shedding in the near wake of a square-section cylinder at incidence [J]. Experiments in Fluids, 2005, 39: 86-98.

[29] Bisset D K, Antonia R A, Browne L W B. Spatial organization of large scale structures in turbulent far wake of a cylinder [J]. Journal of Fluid Mechanics, 1990, 218:439-461.

Effects of boundary layer conditions on aerodynamic forces of a finite-length square prism

WANGHan-feng1,2,YANGFan1,ZOUChao1(1. School of Civil Engineering, Central South University, Changsha 410075, China;2. National Laboratory for High-speed Railway Construction, Changsha 410075, China)

Abstract:The effects of boundary layer conditions on aerodynamic forces of a finite-length square prism were experimentally investigated in a wind tunnel. The width of the tested model d=200 mm, and the aspect ratio H/d=5. The tested Reynolds number based on oncoming flow velocity (U(∞)) and d had a range of 0.68×105 to 5.47 ×105. It was found that Reynolds number has no obvious effects on aerodynamic forces of the finite-length square prism in both uniform flow and turbulent boundary layer; the local aerodynamic forces coefficientsD, and are significantly different along the prism span; both and remarkably increase in turbulence boundary layer relative to those in uniform flow; the bi-stable phenomena of the fluctuating pressure and aerodynamic forces observed in uniform flow disappear basically in turbulent boundary layer; contributions of the symmetrical and asymmetrical wind pressure distribution modes to the pressure fluctuation are determined based on POD analysis; in uniform flow, pressure fluctuations near both ends of the cylinder are controlled by the symmetrical wind pressure distribution, while that at the cylinder mid-span is controlled by the asymmetrical wind pressure distribution; in turbulent boundary layer, asymmetrical pressure distribution controls all wind pressure fluctuations along the height; under both boundary layer conditions, only the asymmetrical POD mode has an obvious periodicity that determines the periodicity of aerodynamic forces, no obvious periodicity is observed for the symmetrical POD mode though it is dominant at some positions.

Key words:finite-length prism; aerodynamic forces; boundary layer conditions; bi-stable phenomenon; POD

中图分类号:TB126

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.05.006

收稿日期：2015-02-02修改稿收到日期：2015-03-20

基金项目：国家自然科学基金资助项目(11472312；51108468)

第一作者 王汉封 男，博士，教授，1976年10月生