多叶光栅叶片端面形状优化设计

周　东　张　辉　叶佩青

清华大学，北京，100084



多叶光栅叶片端面形状优化设计

周东张辉叶佩青

清华大学，北京，100084

摘要：为提高放射治疗剂量的精度，减少因半影导致的剂量误差，引入切割线理论建立了半影解析表达模型。提出了以最大射野范围内半影宽度均值为优化目标，针对圆心偏置的圆弧类端面进行优化设计的方法，并将优化方法应用于中心叶片和离轴叶片的优化设计。结果表明：相比较最大圆弧相交半径法得到的端面形状，采用该算法优化后的叶片半影宽度均值减小了1.6%。

关键词：多叶光栅；叶片端面；半影建模；形状优化设计

0引言

多叶光栅是放射治疗设备实施射束投照的重要执行部件，也是放疗系统中机械结构较为复杂的部件之一。多叶光栅的主要功能是通过叶片运动形成复杂形状的射野，改变射野形状并调制射野范围内投照剂量的分布可满足治疗计划要求，同时尽可能减小正常组织所受剂量。

按照聚焦形式，可将多叶光栅分为单聚焦多叶光栅与双聚焦多叶光栅[1]。按照国际辐射学单位委员会的建议，患者在放射治疗中实际接收的总剂量与计划剂量误差必须在5%以内[2]。叶片端面形状优化设计是多叶光栅设计的重要内容，已产生了多种优化方法[3-4]。目前，研究报道主要集中在基于剂量学实验的端面半影特性研究和基于解析求解的端面优化研究两大方面。

基于剂量学实验的端面半影特性研究中，Huq等[5]对Elekta、Siemens和Varian等公司的6 MV加速器多叶光栅进行了剂量学实验研究，结果表明，半影宽度与多叶光栅相对射线源安装位置相关，离射线源越近，半影宽度越大。Mohan等[6]研究了Varian Clinac 120多叶光栅在6 MV和18 MV光子束下的剂量学特性。对比多种射野限束方法(光阑、MLC、MLC+光阑)后发现，仅采用MLC射野限束方式的半影宽度比其余两种方式的半影宽度大。Wu等[7]研究了叶片端面半影造成的叶片投影位置、光野位置及射野位置之间的差异，并将中心叶片位置偏置的实验结果用于预测离轴叶片的半影特性，提出了离轴叶片位置偏置预测方法。多叶光栅半影受射线源能量分布、多叶光栅叶片端面形状、叶片位置等因素影响显著，因此如何通过端面形状最优设计获取理想半影特性，对实现精确放射治疗意义重大。然而，上述剂量学实验方法研究叶片端面形状对半影的影响时，仅从既定的加速器几何结构物理参数出发，无法对比分析不同叶片形状的半影特性，因此需要借助解析算法实现端面形状优化。

在基于解析求解的端面优化研究方面，Jordan等[8]采用最大圆弧相交半径法求解最优半径值。该方法将射线源视为理想点源，将叶片投影位置处于最大射野处，20%射线衰减线与圆弧端面底边交点重合时对应的半径为理想半径，但仿真分析发现，采用该准则设计的叶片端面半影并不是最优设计。Sun等[9]引入高斯分布射线源，提出了射线追踪算法，研究了直边端面、聚焦端面及圆弧端面对多叶光栅半影特性的影响。Topolnjak等[10]通过几何方法建立了最大相交圆弧半径法的解析求解公式，分离了多叶光栅几何半影及穿射半影，并通过经验公式对总半影宽度进行估算。目前尚未报道包含圆心偏置的端面优化方法，同时未有学者提出并验证端面总半影的解析求解方法。

针对上述研究不足，笔者提出一种通过切割线理论(tangent secant theory，TST)来进行半影解析建模的端面优化方法。首先通过参数辨识获取等效射线源大小及等效路径长度，在此基础上引入优化理论，构造包含圆心偏置的圆弧端面形状优化目标函数和约束条件，并采用基于梯度理论的优化算法进行问题的求解。本研究主要包括三大部分：①提出了基于切割线理论的半影建模方法，并通过Monte Carlo数值仿真验证模型的准确性；②将最大射野范围内的半影宽度均值作为目标函数，将圆心位置及半径作为自变量，基于梯度算法对多叶光栅端面进行形状优化；③建立中心叶片与离轴叶片的几何关系，将优化方法应用于离轴叶片的最优端面设计。

1多叶光栅半影的建模及模型验证

1.1多叶光栅工作原理

多叶光栅通过叶片运动形成射野的工作原理如图1所示。叶片可对射线形成屏蔽，投影平面内的射野形状随多叶光栅叶片位置变化而改变。因此，可根据肿瘤位置规划多叶光栅叶片运动轨迹，确定各个投照角度所需的剂量强度，对肿瘤靶区实现准确剂量投照。本研究将位于中心轴线两侧的叶片定义为中心叶片，将其余叶片定义为离轴叶片。

图1　多叶光栅工作原理

1.2半影解析建模

受射线源能量角度分布、几何结构射线穿射、治疗头散射等因素的影响，射野边缘通常会形成半影。半影宽度一般定义为80%及20%等剂量线间的距离。为行文方便，后续章节中的半影均特指半影宽度。常用多叶光栅半影建模方法主要有Monte Carlo数值仿真、Ray-tracing射线追踪算法等[9-10]。如果半影求解函数较为复杂，则严重制约计算效率，影响优化迭代过程的顺利进行。文献[10]建立了几何半影和穿射半影的解析表达，并将总半影表达为几何半影和穿射半影的加权求和。几何半影的计算需要求取端面切线，穿射半影则需要通过求取割线获取。在上述求解方法的启发下，笔者通过综合几何半影和穿射半影的成因，采用TST求取端面总半影。TST的思想是，通过构建端面的切线和割线，获得半影解析表达模型，其中，切线和割线的位置取决于等效射线源大小以及等效路径长度，可通过参数辨识获取上述模型参数。

坐标系选取如图2所示，定义h1为叶片高度，坐标系原点O位于叶片高度中轴线MN上，叶片端面圆弧圆心Oc相对坐标系原点O在X方向上的偏置为b，圆心Oc与叶片端面顶点T的距离等于圆弧半径R。叶片端面圆弧曲线c=[Rb]T。其中，(x-b)2+y2=R2。以叶片端面Y方向顶点为基准点，叶片行程范围内的起点为Lw，终点为Lp。Lw和Lp分别在探测平面形成投影点Tw和Tp。定义SCD为射线源与中轴线距离，SAD为射线源与探测平面距离，FS为最大射野范围。以叶片处于Tw投影位置为例，采用TST求取半影宽度，算法过程如下。

图2　切割线法半影建模

W(c,Tw)=yP80-yP20

(1)

(2)

(3)

已知射线源且叶片端面形状确定时，投影位置Tw处的半影仅与参数e、l相关。其中，e、l与治疗设备几何参数及射线特性相关，在实际使用中可通过最小二乘拟合参数辨识获取，即求解：

(4)

1.3模型验证

1.3.1数值仿真模型

采用EGSnrc/BeamnrcMonteCarlo仿真软件，建立包含射线源、多叶光栅及探测平面在内的数值仿真模型。多叶光栅最大射野为40cm×40cm，叶片对数为40。本研究采用中间10对叶片形成的10cm×10cm射野。通过改变叶片位置，获得不同投影位置下的半影。记录粒子总数为109。本研究采用加速器参数如下：射线源为单一能量光子源，能量分布为高斯分布，半高全宽为1mm，射线平均能量为1.5MeV，钨合金叶片衰减系数为0.95cm-1，SAD=100cm，SCD=46cm，hl=8cm，FS=40cm[11]。

1.3.2仿真结果半影计算

仿真得到射野范围内射线强度分布，以圆弧半径为10cm，射野范围0～10cm为例，给出仿真数据处理过程，得到叶片投影位置10cm处的射线强度分布，如图3所示。

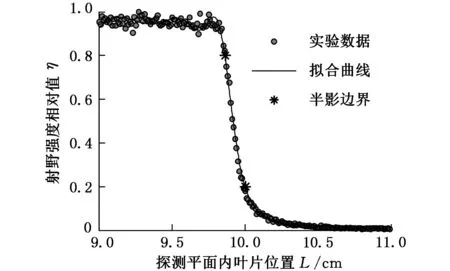
图3　数值仿真数据处理

通过对探测平面的数据进行处理得到半影，处理过程如下：首先对仿真获取的射线强度分布数据点进行曲线拟合，然后计算拟合后的曲线20%及80%射线强度的位置，两者之间的距离即为半影。对图3实验数据进行曲线拟合，得到的半影为1.358mm，拟合方程为

(5)

取n=3，则式(5)中的参数如表1所示。

表1　高斯函数拟合方程参数

1.3.3参数辨识及模型验证

笔者通过改变非圆心偏置圆弧端面叶片的半径，计算不同半径下，随叶片投影位置变化的半影。在此基础上，以仿真数据为参考值，通过最小二乘曲线拟合进行参数辨识，获取切割线法半影模型中的参数e和l。

对于数值仿真模型，通过辨识得到的切割线法半影模型参数e=0.863 mm，l=1.240 cm。从图4中可见，切割线法半影与仿真模型较为吻合。通过分析图形数据发现，两者最大误差为9.50%。

图4　圆弧端面最大射野范围内半影宽度曲线

2中心叶片端面优化

2.1目标函数

多叶光栅端面半影宽度对靶区剂量精度影响显著，小半影可实现较大的剂量梯度，因此本研究以半影均值为目标函数进行优化设计。取最大射野范围内叶片不同的投影位置Ti(i=1，2，…，N)处端面半影为Wi，半影均值为

(6)

(7)

式(7)表示投影位置Ti的坐标取值，其中，X坐标与射线源至多叶光栅距离以及探测平面距离有关，Y坐标在射野范围内作N等分。通过对最大射野范围内叶片投影位置进行均匀分割取样，获取剂量分布数据。

2.2约束条件

圆弧端面形状由圆心半径R及圆心偏置d确定。根据几何关系，可将约束条件分成两类。一类是边界约束：

(8)

另一类是线性约束：

(9)

2.3优化数学模型

为获取探测平面内较小的半影宽度，以半影均值为优化目标，端面优化函数如下：

minμ(c)

(10)

(11)

(12)

(13)

式(11)表示对矩阵中的元素逐一比较。基于上述表达式建立TST半影模型。

2.4优化结果

首先，对射线束中心轴线两侧的中心叶片进行优化分析。选取基于梯度算法的优化算法，将仿真模型及辨识得到的切割线法模型参数代入优化数学模型，通过MATLAB优化程序进行迭代计算。优化后的半影均值为1.261mm，中心叶片圆弧端面优化结果为Ropt=17.306cm，bopt=0.863cm。

计算发现，对于多组不同初值选取，优化结果均收敛于同一点，可见目标函数为凸函数，所得优化结果并没有陷入局部最小值点，因此，该点是全局最小值点。将优化后端面半影计算结果转化为仿真模型参数，如图5所示，可见切割线半影建模与仿真计算结果半影均值较一致。

图5　优化后圆弧端面半影特性与仿真结果比较

将本研究采用的模型参数代入文献[10]的最大圆弧相交半径解析公式计算，得到的最优端面半径为16.183cm，圆心未偏置，相应的半影均值为1.281mm。对比发现，所提出优化方法计算得到的半影均值比最大圆弧相交半径法计算结果更优，半影均值减小了1.6%。

3离轴叶片端面优化

3.1离轴叶片几何模型

按照叶片排布分，多叶光栅可分为水平排布多叶光栅和圆弧排布多叶光栅两种。离轴叶片处于不同几何位置时，叶片高度、叶片与射线源的距离、叶片投影点与射线源的距离均会随叶片排布不同而有所变化。因此，中心叶片端面优化方法在应用于离轴叶片端面设计前，需要根据上述几何关系作修正。

(14)

图6　叶片水平排布及圆弧排布离轴叶片几何模型

同理，对于叶片圆弧排布方式，考察投影位置为PE处的叶片，其相应几何关系为

(15)

3.2离轴叶片优化结果

将不同排布下的几何模型参数代入优化数学模型，通过迭代计算，得到不同叶片投影位置处离轴叶片的最优半径及圆心偏置结果。叶片排布关于射线束中心轴线对称，离轴叶片的投影位置可按单边计算，计算结果如表2、表3所示。

表2　水平排布多叶光栅最优端面　cm

表3　圆弧排布多叶光栅最优端面　cm

由表2、表3可见，对于水平排布多叶光栅，叶片离轴越大，最优半径越大；最大圆心偏置的差值为0.27mm，且叶片离轴越远，圆心沿Y轴负方向偏置越大。对于圆弧排布多叶光栅，最优端面半径离轴叶片与中心叶片最大相差3.27mm，圆心偏置最大相差0.05mm。但与水平排布相反，随叶片离轴越远，圆心沿Y轴负方向偏置越小。

3.3多叶光栅斑马线曲面分析

根据离轴优化结果，采用SolidWorks对优化后的叶片作斑马线曲面分析，如图7所示。斑马线曲面分析结果发现条带间隔较为均匀，端面圆弧过渡较为平稳。

图7　水平排布及圆弧排布端面优化设计斑马线分析

4结语

提出了基于半影建模的多叶光栅叶片端面形状优化设计方法，引入切割线法并建立了半影模型，并通过MonteCarlo仿真验证了模型的准确性。在此基础上，以射野范围内半影均值为目标函数，分别对中心叶片和离轴叶片端面形状展开了优化研究，获取了端面最优圆弧半径及圆心偏置。结果表明，采用该优化算法得到的后端面半影均值比最大圆弧相交半径法得到的计算结果小1.6%。因此，本研究提出的端面优化设计方法为多叶光栅设计提供了新的思路。

参考文献：

[1]崔伟杰，戴建荣. 多叶准直器的结构设计[J]. 医疗装备，2009(2): 4-9.

CuiWeijie，DaiJianrong.StructuralDesignofMultileafCollimator[J].ChineseJournalofMedicalDevice， 2009(2): 4-9.

[2]KleinEE,HanleyJ,BayouthJ,etal.TaskGroup142Report:QualityAssuranceofMedicalAccelerators[J].Med.Phys.，2009, 36(9): 4197-4212.

[3]侯建华，欧宗瑛，宋卫卫. 放射治疗机最佳适形多叶组合光栅叶片形状设计[J]. 大连理工大学学报，2007(6): 840-845.

HouJianhua,OuZongying,SongWeiwei.LeafShapeDesignOptimizationofMultileafCollimatorforConformityinRadiationTherapy[J].JournalofDalianUniversityofTechnology, 2007(6): 840-845.

[4]冯培恩，邱清盈，潘双夏，等. 机械广义优化设计的理论框架[J]. 中国机械工程，2000，11(增刊): 135-138.

FengPeien,QiuQingying,PanShuangxia,etal.TheoreticalFrameofGeneralMechanicalDesignOptimization[J].ChinaMechanicalEngineering, 2000，11(S): 135-138.

[5]HuqMS,DasIJ,SteinbergT,etal.ADosimetricComparisonofVariousMultileafCollimators[J].PhysicsinMedicineandBiology. 2002, 47(12): 159-170.

[6]MohanR,JayeshK,JoshiRC,etal.DosimetricEvaluationof120-leafMultileafCollimatorinaVarianLinearAcceleratorwith6-MVand18-MVPhotonBeams[J].JournalofMedicalPhysics，2008, 33(3): 114-118.

[7]WuJ,LeeT,YehS,etal.ALight-field-basedMethodtoAdjustOn-axisRoundedLeafEndMLCPositiontoPredictOff-axisMLCPenumbraRegionDosimetricPerformanceinaRadiationTherapyPlanningSystem[J].BioMedResearchInternational,2013: 1-8.

[8]JordanTJ,WilliamsPC.TheDesignandPerformanceCharacteristicsofaMultileafCollimator[J].PhysicsinMedicineandBiology,1994, 39(2): 231-251.

[9]SunJ,ZhuY.StudyofDosimetricPenumbraDuetoMultileafCollimationonaMedicalLinearAccelerator[J].InternationalJournalofRadiationOncology,Biology,Physics. 1995, 32(5): 1409-1417.

[10]TopolnjakR,vanderHeideUA.AnAnalyticalApproachforOptimizingtheLeafDesignofaMulti-leafCollimatorinaLinearAccelerator[J].PhysicsinMedicineandBiology, 2008, 53(11): 3007-3021.

[11]RucciA,CarlettiC,CraveroW,etal.UseofIAEA’sPhase-spaceFilesfortheImplementationofaClinicalAcceleratorVirtualSourceModel[J].PhysicaMedica. 2014, 30(2): 242-248.

(编辑张洋)

Shape Optimal Design of Leaf End for Multileaf Grating

Zhou DongZhang HuiYe Peiqing

Tsinghua University，Beijing，100084

Abstract：In order to improve dose delivery accuracy and reduce the dose error caused by penumbra, an analytical penumbra model was presented based on tangent secant theory. With penumbra width mean across radiation field set as objective function, leaf end shape optimization was proposed, which was applied for leaves in the shape of circular arc with center offset from the axis of leaf mean height. Furthermore, shape optimal design of leaf ends for on-axis and off-axis leaves was introduced. Results show that penumbra width mean is reduced by 1.6% for the optimized leaf end, compared with the method of maximum arc intersection radius.

Key words：multileaf collimator; leaf end; penumbra modelling; shape optimal design

作者简介：周东，男，1987年生。清华大学机械工程系博士研究生。主要研究方向为肿瘤放射治疗学、计算机辅助设计与制造CAD/CAM、数字化口腔医学、远区激光熔化快速成形SLM技术。发表论文4篇。张辉，女，1969年生。清华大学机械工程系副研究员。叶佩青，男，1963年生。清华大学机械工程系研究员。

中图分类号：TH122; R815

DOI：10.3969/j.issn.1004-132X.2016.06.006

基金项目：北京市科技计划资助项目(Z141100000514015)；清华大学自主科研计划资助项目(2011Z01013)；清华大学摩擦学国家重点实验室自主研究项目(SKLT12A03)

收稿日期：2015-01-14