基于B—S模型的可转债定价研究

郑雪仪

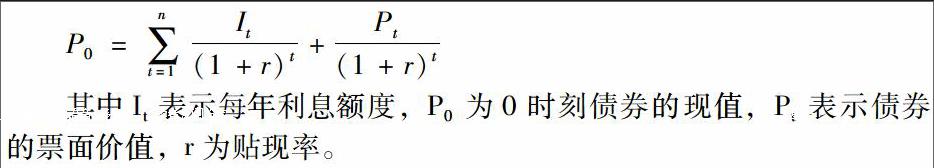
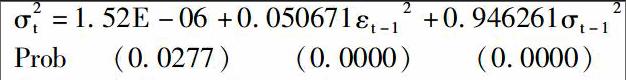
摘 要：随着我国资本市场的不断发展，可转换债券成为筹资和规避风险的重要金融工具，其定价问题日益为各界所关注。本文选择目前主流的布莱克-舒尔斯模型对深机转债进行价格估计，并使用蒙特卡洛方法进行对比估价。结果表明，使用B-S模型对可转债进行定价存在高估现象，但其定价误差远低于由蒙特卡洛法带来的误差。

关键词：可转债定价；Black-Scholes模型；纯债券价值；期权价值；深机转债

一、绪论

（一）研究背景及目的

可转换公司债券，简称“可转债”，是一种与股权相联的债券，具备股票和债券的双重性质，其持有人可以在规定的转换期限内，将债券按既定的转换价格和转换比率转换为公司对应的普通股，享受福利分配和资本增值。

我国第一支上市的可转债是1992年发行的宝安转债，但以转股价过高而夭折。2001年，中国证监会发布了《上市公司可转换公司债券实施办法》等文件，从政策上保证了可转换公司债券的合法市场地位，标志我国可转换公司债券进入规范发展阶段。证监会于2006年5月颁布了《上市公司证券发行管理办法》，进一步规范了可转债发行的条款细则。在完善的政策指引下，可转债市场的规模不断扩大，截至2015年，我国巳累计发行可转债已有100多只。

可转债的最基本问题是定价问题，由于可转债代表公司对自身未来业绩的期许，因此定价对于公司而言十分重要。定价可以决定公司能否真正降低自身成本，正确的定价能够吸引投资者对发行公司的兴趣加大投资规模。我国可转债市场的飞速发展并未得到相应的理论实证研究的同步支持，因此仍需要以我国可转债市场的实际情况入手进行定价研究。

（二）文献综述

早期可转债定价的理论方法主要来自Black和Schole关于期权及公司债券定价的研究。1977年Ingersoll首次将Black-Scholes（简称B-S）模型应用到可转债定价问题中，并提出了基于公司价值的单因素模型，获得定价解析式，但由于可转债的条款过分复杂，导致解析式的难获得。许多学者在考虑利率、股价、波动率和等多个因素的基础上，提出更为复杂的定价模型。Brennan将利率引入先前的定价模型中，形成公司价值和利率的双因子定价模型。2008年，Paclokovalov则进一步将股价、波动率、利率和信用风险作为四大因素实现可转债价格的估计。

中国学者对可转债定价的研究始于21世纪初，一般是以国外研究方法为参照，进而结合国内实际情况来应用。杨如彦等人选择股票数据作为录入数据，使用CIR利率期限模型建立了双因素模型，结果发现利率对可转债的价格影响甚小。刘毅和陈瑶（2011）在考虑可转债的路径依赖性后使用最小二乘的蒙特卡洛方法进行定价，冯玥（2010）使用二叉树对工商银行的可转债进行定价。李茂盛（2012）使用B-S模型和参数模拟理论方法对可转债进行定价，发现理论价格与实际仍有一定偏差。龚其国通过蒙特卡洛方法发现其对可转债的估算效果甚好。

二、定价模型

目前，还没有一个统一的定价模型能够完整地包含所有可能的条款假设。根据可转债的特性，研究中主要针对可转债的期权部分定价，下面介绍蒙特卡洛模拟法及B-S模型。

（一）蒙特卡洛模拟法

蒙特卡洛模拟在进行期权估值时利用风险中性股指结论。通过模拟变量的很多途径，得出风险中性世界的期望损益进而使用无风险利率进行贴现。使用蒙特卡洛进行模拟的步骤如下：（1）模拟股价s的一种随机抽样路径；（2）计算该路径下的衍生品损益；（3）重复前两步得到多组关于衍生品损益的样本；（4）计算样本损益的平均值作为风险中性世界的期望损失估计值；（5）使用无风险利率作为贴现，得到衍生品的估计值。

该方法的优势在于不管损益依赖的s路径如何改变，其只依赖于s的最终价值。当股票的预期收益率和波动率函数十分复杂时，蒙特卡洛的优势更加明显。蒙特卡洛方法适用于欧式期权的定价。

（二）Black-Scholes模型

Black-Scholes模型于20世纪70年代初由Fischer Black、Myron Scholes和Robert Merton共同提出。该模型操作相对简单，称为许多衍生品定价的重要参照模型。

以不支付红利的欧式看涨期权为例。假设股票当前价格为S，股票预期收益率为μ，股票价格波动率为σ，则股票价格遵从几何布朗运动。

若用f表示期权价值，则f必然是S和t的某一函数，因此可以推导出B-S-M微分方程如下：

在0时刻不支付红利的股票欧式看涨的B-S定价公式分别如下：

c=SN（d1 ）-Ke-rTN（d2）

其中r表示无风险利率，K表示执行价格，N（d）表示标准正态分布的累积分布函数。d1和d2计算如下：

d1=ln（SK）+（r+σ22）TσTd2=d1-σT

其中σ表示股价波动率，T是期权到期期限，用年表示。

可转债中的期权部分实际上就是一种看涨期权，因此可以使用B-S定价公式对可转换债券的期权部分定性定价。B-S公式所设计计算相对简单，公式中所用参数大部分可直接在市场中获得，而波动率需要根据需求选择历史波动率或隐性波动率代入计算。该模型对于欧式期权定价尤其合适。

B-S模型属于解析方法，蒙特卡洛方法属于数值方法，蒙特卡洛方法可通过加大运算次数来提高精准度，但在运算过程中工程量相对较大。B-S方法则作为唯一的解析法，解析解本身不会产生误差，但是该方法对于美式期权的处理较为费力，并且需要满足一定的前提条件。

三、可转换债券价值分析

由于B-S作为唯一的解析法，能够得到套期保值参数和杠杆效应的解析表达式，鉴于在我国的特殊情况，本文选择B-S模型进行深机转债的实证研究。

可转换债券相当于一个内嵌看涨期权的金融衍生产品，因此可将可转换债券分解为纯债券价值和期权价值两个部分，可转债的价值由这两部分加总得来。

深机转债的基本资料：1、代码简称：深机转债；2、存续期间（年）：6；3、发行日期：2011-07-15；4、面额：100；5、初始转股价：5.6600；6、票面利率：第一年为0.6%，第二年为0.8%，第三年为1.0%，第四年为1.3%，第五年为1.6%，第六年为1.9%。

以下小节将以深机转债为例对其2014年12月1日进行可转债的价值计算。

（一）纯债券价值

纯债券价值相当于投资于一般债券时可获得的现金流的现值，计算公式如下：

P0=∑t=1nIt（1+r）t+Pt（1+r）t

其中It表示每年利息额度，P0为0时刻债券的现值，Pt表示债券的票面价值，r为贴现率。

深机转债的票面利率采用逐年递增的模式，因没有六年期国债，因此采用2011年起期限与之相近的五年期国债作为贴现率（为6%），由于国债是单利，因此转换为按年度复利的利率为5.26%。计算得出债券的纯债券在发行（2011年）时的价值为79.37元。根据贴现率计算出在2014年12月份时的纯债券价值为92.56元。

（二）期权价值

B-S模型是对期权的一种有效计算方式，根据公式需要对几个参数进行事前设定。（1）转股价格K：深机转债的初始转股价为5.66元/股。该价格可作为期权的执行价格。（2）股价波动率σ：股价波动率σ是估价过程的重要参数。GARCH（广义自回归条件异方差）模型可以很好刻画波动率聚集性，从而对股票价格的波动率产生很好的预测作用。

深机转债对应的股票是深圳机场，可使用深圳机场的股票收盘价数据进行波动率的计算。本文将选用2011年1月4日到2015年5月13日间的1056个收盘价数据作为样本数据，使用EVIEWS软件进行股价波动率的估算。可得波动率方差如下，

等式中参数均显著通过检验，通过GARCH模型所得深圳机场股票价格的波动率为0.351936。

（3）无风险利率r：在本文采用2014年的一年期定期存款利率作为无风险利率3%，转化为连续复利的无风险利率为2.96%。（4）剩余期限T：余期限使用年作为单位，本文以深机转债2014年12月1的转债价值为例，因此剩余期限为2.622263年。（5）转股比例n：转股比例为债券面值/转股价格，则深机转债的转股比例n为100/5.6600=17.6678。即一份债券包括看涨期权17.6678份。

将参数带入B-S定价模型中，得出深机转债的单位期权价值为1.5794，一份债券对应的期权为17.6678份，则单位可转债的可转期权价值为1.5794*17.6678=27.9046。

（三）可转债理论价格

根据3.1和3.2部分计算所得，深机转债在2014年12月1日的理论价格=纯债券价格+期权价值=92.56+27.9046=120.46。当日深机转债的实际股价为117.25，两者存在一定较小误差。

使用蒙特卡洛方法对深机转债进行模拟定价，得出的可转债价值：单位期权为0.2，转股比例为17.6678，期权价值为，可转债价值为96.09，实际价值为117.25。

深机转债使用B-S方法进行期权部分价值计算，所得理论价值与实际价值之间的误差为2.74%，使用蒙特卡洛方法进行同等期权部分价值的估计，所得理论价值与实际价值之间误差为-18.04%，远大于前一种方法所带来误差。

四、结论

根据上节的实证结果可得出如下结论：使用蒙特卡洛容易造成对期权价值的低估，从而导致理论价值相对于实际价值偏低，而是用B-S模型所估算的期权价值相对较高，因此导致其理论价值相对于实际价值偏高，从而造成债券价值的高估。不论是使用哪种方法均会存在一定的估值误差，除了模型本身条件受限外，可能与我国市场的不完整有关。首先是我国的可转债加入了诸如回售权和转股价格调整等，这些会影响到定价的准确性。其次，本文所用的是6年期债券，在估算纯债券的价值时选择的贴现率为5年期国债，不可避免会带来定价的偏差。另外我国的资本市场以中小投资为主，存在很大的投机性，更容易产生波动。

参考文献：

[1] 赵洋， 赵立臣，基于蒙特卡罗模拟的可转换债券定价研究[J]，系统工程学报， 2009，24（5）：621 - 625.

[2] 黄靖贵，杨善朝，冯霞，具有动态信用风险的可转债的定价研究[J]，数理统计与管理， 2008，27（6）：1108 - 1116.

[3] 唐文彬，张小勇， LSM可转债定价模型及其应用研究[J]，财经理论与实践，2008，

[4] 汤洁，B-S模型在可转换债券定价中的应用研究[J]，时代金融，2015第2期

[5] 冒小栋，朱晨晨，我国可转换债券的发展路径即定价研究[J]，时代金融，2014年第4期

[6] 龚其国，陈凉，我国上市公司可转债定价及实证研究[J]，现代管理科学，2014年第5期