声子晶体结构在换能器匹配层中的应用

唐一璠， 林书玉

(陕西师范大学 物理学与信息技术学院, 陕西 西安 710119)



声子晶体结构在换能器匹配层中的应用

唐一璠， 林书玉*

(陕西师范大学 物理学与信息技术学院, 陕西 西安 710119)

摘要：将声子晶体结构用于换能器匹配层中, 利用声子晶体的能带特性改善换能器的匹配性能。研究了厚度振动超声换能器中声子晶体型匹配层的参数变化对换能器频带宽度、发射电压响应和辐射特性的影响，建立了声子晶体型匹配层厚度振动换能器等效电路模型,并利用传输矩阵计算了匹配层的声能量透射系数。研究结果表明: 合理选择声子晶体型匹配层的材料和厚度，可以使换能器的频带宽度扩大一倍；并且将换能器的共振频率处于声子晶体结构的通带范围内，可以使声能量透射系数接近于1。

关键词:声子晶体； 匹配层； 频带宽度； 发射电压响应； 辐射特性

PACS: 43.20.+g,3.40.+s,63.20.-e

超声换能器是在超声频率范围内将交变的电信号转换成声信号或者将外界声场中的声信号转换为电信号的能量转换器件。当换能器将声波辐射到低阻抗的流体载荷中(通常是水)时，由于陶瓷和水介质之间的声阻抗不匹配，弹性波将在分界面处发生反射，故需要加入匹配层[1-3]。匹配层是在换能器辐射端粘结特性阻抗介于陶瓷和辐射负载介质之间的一种或多种材料，其设计的主要目的是：满足换能器和辐射负载之间的声学匹配要求, 使声波能量最大限度地向负载介质进行辐射[4-6]。匹配层技术是拓宽厚度振动换能器宽带的有效方法之一，在单谐振条件下的辐射端每增加一个匹配层就增加一个附加谐振模[7-8]。在医学超声和检测超声中由于压电材料的声阻抗率较高，为了更好实现人体组织声匹配，声匹配层的应用频率范围已从早期的小于2.5兆赫兹[9]发展到接近于百兆赫兹[10]的超高频段。

声子晶体是弹性常数、质量密度等参数周期性变化的一种新型材料。当声波或弹性波在其中传播时,受其内部周期性结构的作用,会形成一种分离的特殊色散曲线,色散曲线之间的频率范围称为带隙,而色散关系曲线上的频率范围则称为通带。根据带隙频率所对应的波长与晶格常数的比例关系，带隙可分为Bragg 散射型和局域共振型，局域共振型声子晶体由刘正猷等人于2000年提出[11]，根据声子晶体的通带特性可以制造出透射率高的新型材料[12]。

现在大部分换能器使用的都是单层匹配系统，因为多层匹配中压电陶瓷片与匹配层、匹配层与匹配层间需要粘结胶层，这就影响了换能器匹配层的匹配性能，会造成一定的误差，想要制造极薄的粘结胶层在工艺上也很难实现。而当采用声子晶体型换能器匹配层时，我们可以把粘接胶体当成声子晶体周期性材料的一种，这样就可以从根本上解决粘结胶体带来的误差。本文利用等效电路法计算出声子晶体型换能器匹配层的电导曲线和发射电压级响应曲线，得出在同等条件下可以使换能器的频带宽度扩大一倍左右；同时利用声传输矩阵,计算声子晶体型匹配层下的声波传输，对于合理的匹配层材料特性和厚度, 可以使声能量透射系数接近于1。

1声子晶体型换能器匹配层的

等效电路模型

如图1所示，压电陶瓷圆片厚度振动换能器的半径为32 mm、厚度为5.8 mm，匹配层A、B组成了一个周期为2的有限声子晶体结构，负载为水。

图1　声子晶体型换能器匹配层几何示意图

为了研究匹配层参数变化引起的厚度振动换能器共振频率的变化，我们建立了换能器的机电等效网络，通过等效电路得到换能器的导纳曲线和发射电压响应曲线。通常宽频带主要反映在电导频响曲线和发射电压响应曲线上。在电导曲线中低于最大响应3 dB的两个频率差定义为换能器的频带宽度。发射电压响应曲线则包含一定电压下将电功率转化为声功率的效率信息。图1对应的一维等效电路模型如图2所示。

图2声子晶体型换能器匹配层等效电路模型

Fig.2Equivalent circuit model of the acoustic phonon crystal type transducer matching layer图2中压电陶瓷片的负载阻抗为：

Z1=jρctstan(kl/2)；

(1)

Z2=ρcts/[j sin(kl)]。

(2)

压电陶瓷片的静态电容和机电转换系数为：

(3)

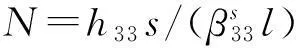
(4)

压电陶瓷片的纵波波速和波数为：

(5)

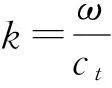
(6)

图中匹配层A、B的等效阻抗分别为：

Zp1=jρ1c1stan(k1l1/2);

(7)

Zp2=ρ1c1s/[jsin(k1l1)];

(8)

Zp3=jρ2c2stan(k2l1/2);

(9)

Zp4=ρ2c2s/[j sin(k2l2)]。

(10)

图2中匹配层A、B的纵波波速和波数分别为：

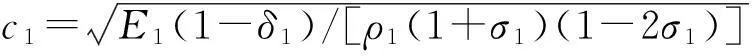
(11)

(12)

(13)

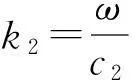
(14)

以上公式中匹配层A各部分的参量ρ1、s、l1、E1、σ1分别为密度、面积、厚度、杨氏模量和泊松比。匹配层B各部分的参量ρ2、s、l2、E2、σ2分别为密度、面积、厚度、杨氏模量和泊松比。

由于圆盘的直径远大于圆盘的厚度，则换能器可视为无限大障板上圆形活塞的辐射，在高频辐射时，活塞辐射阻为Zf=ρ0c0s，其中ρ0、c0、s分别为水的密度、声速和面积。

等效电路中不同位置的阻抗为：

Za=Zp3+(Zf+Zp3)Zp4/(Zf+Zp3+Zp4);

(15)

Zb=Zp1+(Za+Zp1)Zp2/(Za+Zp1+Zp2);

(16)

Zc=Zp3+(Zb+Zp3)Zp4/(Zb+Zp3+Zp4);

(17)

Zd=Zp1+(Zc+Zp1)Zp2/(Zc+Zp1+Zp2);

(18)

(19)

其中Za、Zb、Zc、Zd、Ze分别为不同层数匹配层下的负载阻抗。

等效电路的总阻抗Z和总电导G分别为：

Z=Ze/(1+jωCoZe);

(20)

G=1/Z。

(21)

则由以上式子可以得出换能器辐射器面端振速vs和平均声功率W为:

(22)

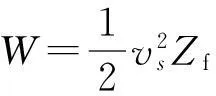
(23)

其中Vi代表换能器的电压，在小信号激励时,压电换能器的发射指向性指数D和电压发射响应级为S为

(24)

S=10lgW+D+159.8。

(25)

1.1无匹配层时的电导曲线.

压电陶瓷片半径为32 mm、厚度为5.8 mm，后端自由，前段负载为水，无匹配层的电导曲线, 如图3可以看出电导带宽大约为11 kHz。

图3　厚度振动无匹配层的电导曲线

1.2环氧树脂和聚苯乙烯组成的声子晶体型匹配层

采用声子晶体型匹配层后, 该声子晶体中材料A为环氧树脂,B为聚苯乙烯,声子晶体的左端是压电陶瓷片，右端是水负载。计算时取2个周期,环氧树脂的密度为1 180 kg/m3,声速2 535 m/s, 聚苯乙烯的密度1 050 kg/m3,纵波波速为2 400 m/s。我们取了3种不同厚度的组合方式：声子晶体1、声子晶体2、声子晶体3对应的晶胞系数分别为7.16、3.55、5.54 mm。其中环氧树脂的厚度为6.16、1、4.54 mm，对应的聚苯乙烯的厚度为1、2.55、1 mm。从图4中可以看出，拓宽频带效果最好的是晶胞系数为7.16 mm，其最大电导值一半所对应的频率分别为215 kHz和234 kHz，则电导带宽为19 kHz。可以看出增加声子晶体型匹配层后，换能器一阶共振频率和二阶共振频率均移向低频，并且在一阶共振频率附近出现二阶共振频率，使得单峰变成了双峰，说明声子晶体型匹配层能够有效拓展带宽。

图4　匹配层在不同厚度下的电导曲线

根据我们取的3种不同厚度的组合方式，得到了它们的发射电压响应曲线(如图5所示)，发射电压响应带宽越平稳越能反映换能器的收发性能。从图5中可以看出晶胞系数为7.16 mm时，最大发射电压响应为125.2 dB，此时对应的频率为216.5 kHz,其-3 dB带宽达到最大，为18 kHz，说明在这个频带范围内换能器的收发性能最好。

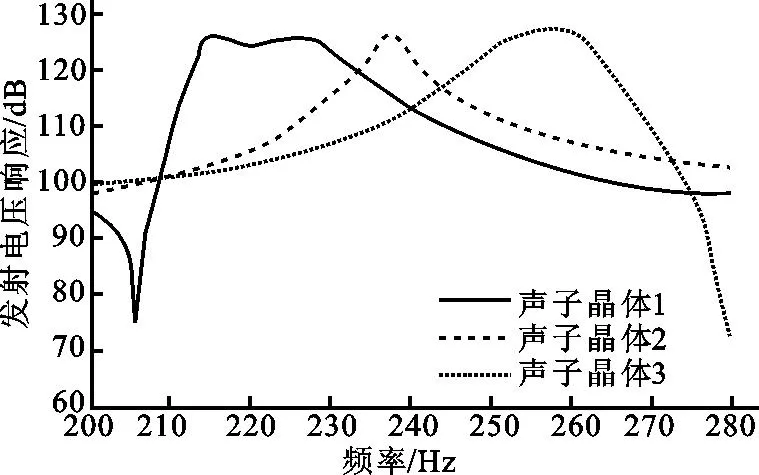
图5　匹配层在不同厚度下的发射电压响应曲线

1.3有机玻璃和环氧树脂组成的声子晶体型匹配层

取有机玻璃的密度1 190 kg/m3,纵波波速为2 730 m/s。我们同样取了3种不同厚度的组合方式：声子晶体1、声子晶体2、声子晶体3对应的晶胞系数分别为6.78、3.8、5.88 mm。其中有机玻璃的厚度分别为6.66、1、4.88 mm，对应的环氧树脂的厚度分别为1、2.8、1 mm。从图6中可以看出，拓宽频带效果最好的是晶胞系数为6.78 mm，最大电导值一半所对应的频率分别为213和231 kHz，则电导带宽为18 kHz。

图6　匹配层在不同厚度下的电导曲线

在小信号激励电压为3.54 V时，根据我们取的3种不同厚度的组合方式，从图7中可以看出，最大发射电幅压响应为124.2 dB，此时对应的频率为215 kHz,其-3 dB带宽达到最大，为18 kHz。整个带内较平坦,是工程应用中实现换能器宽带性能的较好选择。

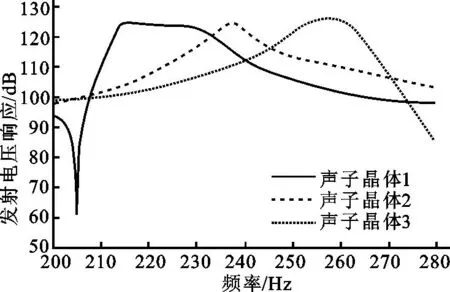
图7　匹配层在不同厚度下的发射电压响应曲线

2计算声子晶体型匹配层的

声能量透射系数

根据声子晶体的能带特性，我们可以将换能器的共振频率处于声子晶体的通带范围内，使声子晶体的能带特性和换能器的匹配性能有机结合，因此我们利用传输矩阵计算了声子晶体型匹配层的声能量透射系数，其示意图如图8所示。

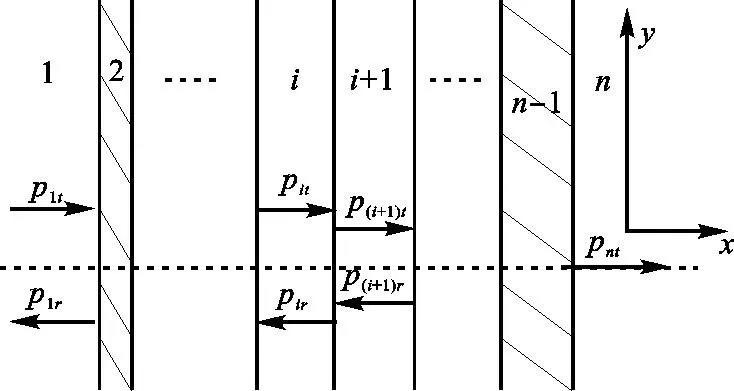
图8　多层介质声波反射和透射

设第i匹配层内声压分布和质点振速的表达式为：

pi=pitaej[ωt-ki(x-li-1)]+piraej[ωt+ki(x-li-1)];

(26)

(27)

pita、pira、Ri分别为第i层的入射声压幅值、反射声压幅值和介质的特性阻抗，li代表第i层的厚度。

设第i+1匹配层内声压分布和质点振速的表达式为:

pi+1=p(i+1)taej[ωt-k(i+1)(x-li)]+

p(i+1)raej[ωt+k(i+1)(x-li)];

(28)

p(i+1)raej[ωt+k(i+1)(x-li)])。

(29)

p(i+1)ta、p(i+1)ra、Ri+1分别为第i+1层的入射声压幅值、反射声压幅值和介质的特性阻抗。

第i层和第i+1层介质的声学边界条件为:

pi|x=li=p(i+1)|x=li;

(30)

vi|x=li=v(i+1)|x=li。

(31)

将以上各式整理可得

(32)

(33)

传递矩阵为

(34)

对于n层透射介质，声压可以由以下矩阵方程计算:

(35)

声强透射系数为

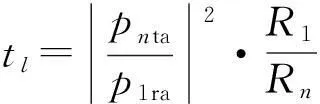
(36)

当使用声子晶体型匹配层时可以直接得出其声强透射系数为

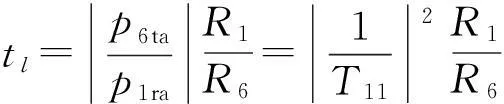
(37)

2.1无匹配层时的透射系数

以换能器对水辐射为例, 选用PZT4压电陶瓷材料, 半径为32 mm、厚度为5.8 mm。换能器发射声波频率为351 kHz, 当无匹配层时压电陶瓷超声换能器匹配层的透射系数为0.159,声能量辐射效率很低, 不能达到较好的匹配。

2.2有机玻璃和环氧树脂组成声子晶体结构的声能量透射系数

换能器发射声波频率为351 kHz,多层匹配为声子晶体结构, 该声子晶体中材料第一层为有机玻璃,第二层为环氧树脂,声子晶体的左端是压电陶瓷片，右端是水负载，计算时取2个周期。图9给出了3组在通带时对应两种材料厚度的最佳匹配方式：声子晶体1、声子晶体2、声子晶体3对应的晶胞系数分别为2.92、4.56、6.53 mm，其中有机玻璃层厚度分别为2.38、1.52、2.37 mm，对应的环氧树脂层厚度可以取0.54、3.04、4.16 mm。从图9中我们可以看出随着有机玻璃与环氧树脂厚度的变化，声子晶体型匹配层的声能量透射系数随之变化，计算结果表明声能透射系数最大值为0.568。

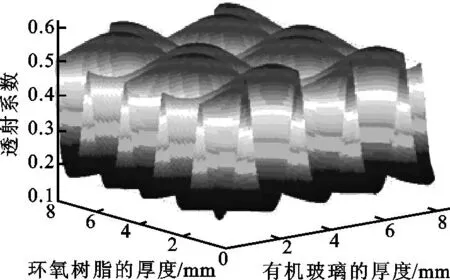
图9　声子晶体结构的声能量透射系数

对应于3组在通带时2种材料厚度的最佳匹配方式,我们给出了声能量透射系数随频率变化的曲线(如图10所示)，从图中可以看出在晶胞系数为2.92 mm时，换能器的声能量透射系数随频率的变化相对平稳一些。

图10　声能量透射系数随频率的变化

2.3铝和环氧树脂组成声子晶体结构的声能量透射系数

换能器发射声波频率为351 kHz,多层匹配为声子晶体结构, 该声子晶体中材料第一层为铝,第二层为环氧树脂，铝的密度为2 730 kg/m3,纵波波速为6 300 m/s。计算时取2个周期调整铝和环氧树脂的厚度, 可使换能器对负载介质有较大的能量输出。给出了3组铝和环氧树脂的最佳匹配方式：声子晶体1、声子晶体2、声子晶体3对应的晶胞系数分别为1.38、4.97、11.21 mm，其中铝层厚度分别为1.01、0.98、7.99 mm，对应的环氧树脂层厚度可以取0.37、3.99、3.22 mm。从图11中我们可以发现在不同厚度下声子晶体的能带特性，当在通带时声能透射系数的最大值为0.999，可见声子晶体多层匹配结构可以大幅提高换能器的声透射系数。

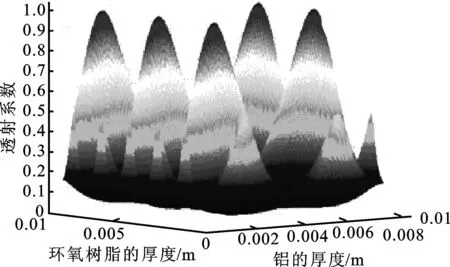
图11　声子晶体结构的声能量透射系数

根据在声能量透射系数最大时得出的铝和环氧树脂三组不同厚度值，我们可以画出在这三组不同厚度时它们的声能量透射系数随频率的变化曲线。从图12中可以看出在晶胞系数为1.38 mm时，换能器的声能量透射系数随频率衰减最小。

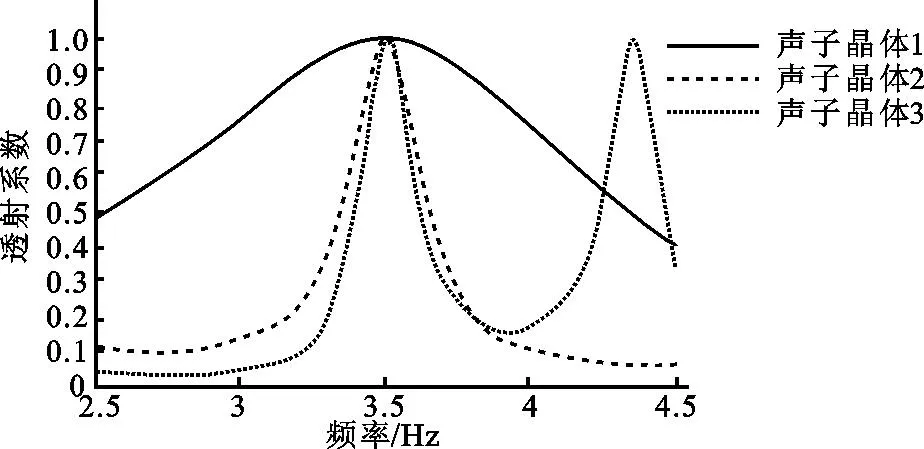
图12　声能量透射系数随频率的变化

3结论

为了研究声子晶体的能带特性与换能器的匹配性能，本文将声子晶体结构用于换能器匹配层中, 建立了声子晶体型匹配层厚度振动换能器等效电路模型,并利用传输矩阵计算了匹配层的声能量透射系数。研究结果表明: 采用铝和环氧树脂的最佳匹配组合方式可以使声能量透射系数从原来为0.159扩大至0.99，说明换能器处于共振频率时向声子晶体的通带中辐射声波，可以大幅提高声能量透射系数;采用环氧树脂和聚苯乙烯组成的声子晶体型匹配层，可以使换能器的频带宽度从原来的11 kHz扩大至18 kHz左右，换能器一阶共振频率和二阶共振频率均移向低频，并且在一阶共振频率附近出现二阶共振频率，使得单峰变成了双峰，说明声子晶体型匹配层能够有效拓展带宽。本文的局限在于仅研究了一维声子晶体做换能器匹配层时的情况，而没有研究当匹配层为二维和三维声子晶体时换能器的匹配性能，在以后的工作中，我们会将二维和三维声子晶体用于换能器的匹配层中。

参考文献:

[1] 林书玉.超声技术的基石：超声换能器的原理及设计[J].物理，2009,38(3):141-148.

[2] QIAN Y, HARRIS N R. Modelling of a novel high-impedance matching layer for high frequency (>30 MHz) ultrasonic transducers[J].Ultrasonics,2014,54:586-591.

[3] CHEN S, ZHANG Y H.Functionally graded materials for impedance matching in elastic media[J].Physics Letters A,2014,378:77-81.

[4] 俞宏沛,宋兰英.采用多模振动拓宽换能器频带的几种方法[J].声学与电子工程,1999,55(3):23-27.

[5] 滕舵,陈航,张允孟.宽带纵振Tonpilz型水声换能器的优化设计[J].声学技术,2005,24(1):58-60.

[6] 林书玉.超声换能器的原理及设计[M].北京:科学出版社,2004:230.

[7] 陈航,张允孟,李志舜.具有阻抗匹配层的宽带纵向振动压电换能器设计[J].应用声学,2001,20(2):31-34.

[8] 徐钧,俞宏沛,李建成.纵振换能器拓宽频带的方法综述[J].声学与电子工程,2003,72(4):17-21.

[9] SABER S, AMIR A. Determination of acoustic impedances of multi matching layers for narrowband ultrasonic airborne transducers at frequencies <2.5 MHz:application of a genetic algorithm[J].Ultrasonics,2012,52:169-185.

[10] SABER S, AMIR A, RAMZI O. Influence of the thickness of matching layers on narrow band transmitter ultrasonic airborne transducers with frequencies <100 kHz: application of a genetic algorithm[J].Applied Acoustics,2014,75:72-85.

[11] KUSHWAHA M S,HALEVI L,DOBYNSKI T,et a1. Acoustic band-structure of periodic elastic composites[J]. Physical Review Letters,1993,71(13):2022-2025.

[12] 温熙森,温激鸿,郁殿龙,等.声子晶体[M].北京:国防工业出版社,2009.

〔责任编辑 李博〕

Application of the phononic crystal structure in the transducer matching layer

TANG Yifan, LIN Shuyu*

(School of Physics and Information Technology, Shaanxi Normal University,Xi′an 710119, Shaanxi, China )

Abstract:Phononic crystal structure is used in the matching layer of the transducer.The energy band characteristics of the phonon crystal and the matching performance of the transducer are combined to improve the ability of transducer.The influence of the phononic crystal structure parameters on the band width, the transmission voltage response and the radiation characteristics of the ultrasonic transducer are investigated. The equivalent circuit model of the vibration transducer with the thickness of the phonon crystal shape matching layer is established, and transmission matrix is used to calculate the transmission coefficient of acoustic energy of matched layers.The results show that reasonable material and thickness phonon crystal shape matching layer can make the transducer with broad frequency band.When the resonance frequency of the transducer is in the range of the phonon crystal structure, the acoustic energy transmission coefficient can reach to 1.

Keywords:phononic crystal; matching layer; band width; emission voltage response; radiation characteristics

中图分类号:O426.2

文献标志码:A

*通信作者：林书玉，男，教授，博士生导师。E-mail: sylin@snnu.edu.cn

基金项目：国家自然科学基金(11174192,11374200,11474192)

收稿日期：2015-10-20

doi:10.15983/j.cnki.jsnu.2016.02.224

文章编号：1672-4291(2016)02-0037-06

第一作者： 唐一璠，男，硕士研究生，研究方向为功率超声。E-mail:519929775 @qq.com