基于蒙特卡罗法的辐射热防护测试仪的数值分析

万贤福， 汪　军， 黄　伟

(1. 浙江省新型纺织品研发重点实验室， 浙江 杭州 310001; 2. 东华大学 纺织学院， 上海 201620)



基于蒙特卡罗法的辐射热防护测试仪的数值分析

万贤福1, 2， 汪军2， 黄伟2

(1. 浙江省新型纺织品研发重点实验室， 浙江 杭州 310001; 2. 东华大学 纺织学院， 上海 201620)

摘要：为了探讨辐射热防护测试(RPP)仪在试样表面产生的辐射热通量分布，采用蒙特卡罗法对RPP建立了数值模型，并进行了实验验证. 计算结果与实验结果十分吻合，证明了模型的合理性与正确性. 计算结果显示，在试样的入射表面，辐射热通量呈椭圆形分布，能量集中在内部区域，在中心区域的辐射热通量分布相对均匀，两侧边缘的辐射热通量相对较低. 研究结果为进一步研究RPP测试试样的防护效果提供了理论依据.

关键词：辐射热传递； 辐射热防护； 辐射热通量； 蒙特卡罗法

辐射热防护性能广泛应用于评价火灾防护服的防护热辐射伤害的能力[1]. 为了获取这一指标，人们设计出辐射热防护测试(RPP)仪进行检测[2]. RPP仪产生均匀分布的辐射热通量，并将试样暴露在此辐射热通量之下，检测穿过试样的辐射热通量，然后基于Stoll曲线预测皮肤发生二度烧伤的时间[3-4]. 由于Stoll曲线是基于皮肤直接暴露于均匀分布热通量的情形下的实验数据, 因此，RPP仪准确预测热辐射皮肤烧伤的关键在于仪器产生均匀分布的辐射热通量. 尽管文献[2]给出了RPP仪的设计规范，以保证测试结果的准确与一致. 然而在实际的测试中，通过观察试样烧伤程度的分布可以发现，辐射热通量并非均匀一致. 由于入射辐射热通量的分布情况是测试面料的热防护效果的一个重要决定因素，因此，本文尝试对RPP仪产生的辐射热通量进行数值分析，旨在探讨试样表面的入射辐射热通量的分布情况，为后续分析RPP仪测试面料的热防护性能做准备. 由于蒙特卡罗法在大量复杂问题中所表现出的优异性[5-7]，本文采用蒙特卡罗法进行建模.

1模型

1.1模型描述

RPP仪的结构如图1所示，基本由石英灯阵列、灯箱、隔热板、挡板、试样夹板以及传感器等组成. 石英灯管为热辐射源，发出热辐射；石英灯管置于灯箱之内，灯箱的一侧装有隔热板，用于阻隔热量，以防止试样一侧过热；挡板用于遮挡热辐射，当测试开启，挡板迅速被提升，从而将试样直接暴露在石英灯管产生的热辐射之下；试样被夹在试样夹板1和2之间，传感器则放置在试样夹板2的后侧.隔热板和试样夹板都开有一定大小的窗口，测试时，热辐射穿过这些窗口最终抵达热通量传感器表面.

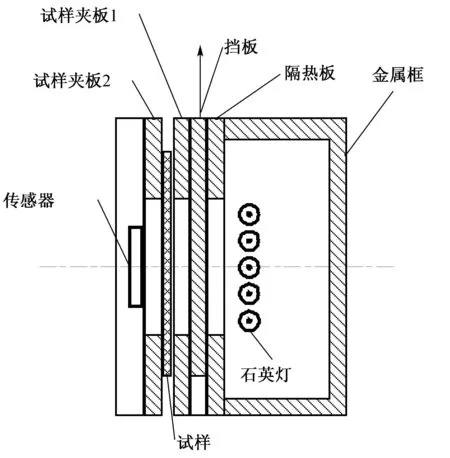
图1　RPP仪的结构示意图Fig.1　Schematic for the RPP apparatus

由于RPP仪仅检测热辐射的影响，而由热对流产生的影响则消除，在灯箱壁面设置有垂直方向的通风对流口，通过灯箱内垂直方向的机械对流以消除热对流作用于灯箱外的试样表面. 石英灯管壁面与灯箱内壁对流的存在，使得对流与辐射耦合，问题变得复杂，为了简化，灯管温度与灯箱内壁的温度通过测试手段获得，成为已知条件，将问题转变成纯辐射问题. 除此之外，本模型为了进一步简化问题还做出如下假设：

(1) 壁面均为漫射表面；

(2) 空气与石英灯管内气体不参与热辐射，它们对热辐射透明；

(3) 石英对于不同波段的热辐射或者完全透明，或者完全不透明，石英介质不参与热辐射的吸收与散射，热辐射的发射、吸收与反射均发生在气、固或固、气界面上；

(4) 壁面的温度分布均匀；

(5) 钨丝表面的发射为漫反射；

(6) 钨丝和石英灯管两端的影响可以忽略不计；

(7) 壁面上的垂直通风孔泄漏的热辐射可以忽略不计.

基于上述假设，本文采用蒙特卡罗法建立了RPP仪的热辐射模型. 虽然RPP仪不仅仅在内部产生热辐射用于检测，其外壳也对外部环境释放热辐射，然而外部热辐射并非用于测试，这不是本文关注的问题，所以本文模型并不给予考虑. 此外，本文仅关注由RPP仪产生的用于测试的热辐射，并不关注热辐射在试样内部的传播. 因此，本文模型所模拟的问题如下：当测试开始时，挡板去除，热辐射首先由石英灯发出，然后在4个相连的腔体(灯箱、隔热板窗口、挡板室和试样夹板窗口)内传播，最后到达试样表面. 由于腔体壁面吸收热辐射后，温度升高，成为了第二辐射源.

蒙特卡罗法把热辐射看成大量能量粒子的随机传播行为，其模拟的过程主要包括：各种表面和形体的几何描述，发射、反射、折射和散射的概率模型，能量粒子轨迹与表面、形体的相交判断与求解等. 标准蒙特卡罗法的这些细节工作在文献 [5-7]中都已描述，在此不再赘述. 由于石英灯的模拟在本模型中比较复杂，因此，本文主要对其进行详细阐述.

1.2石英灯模型

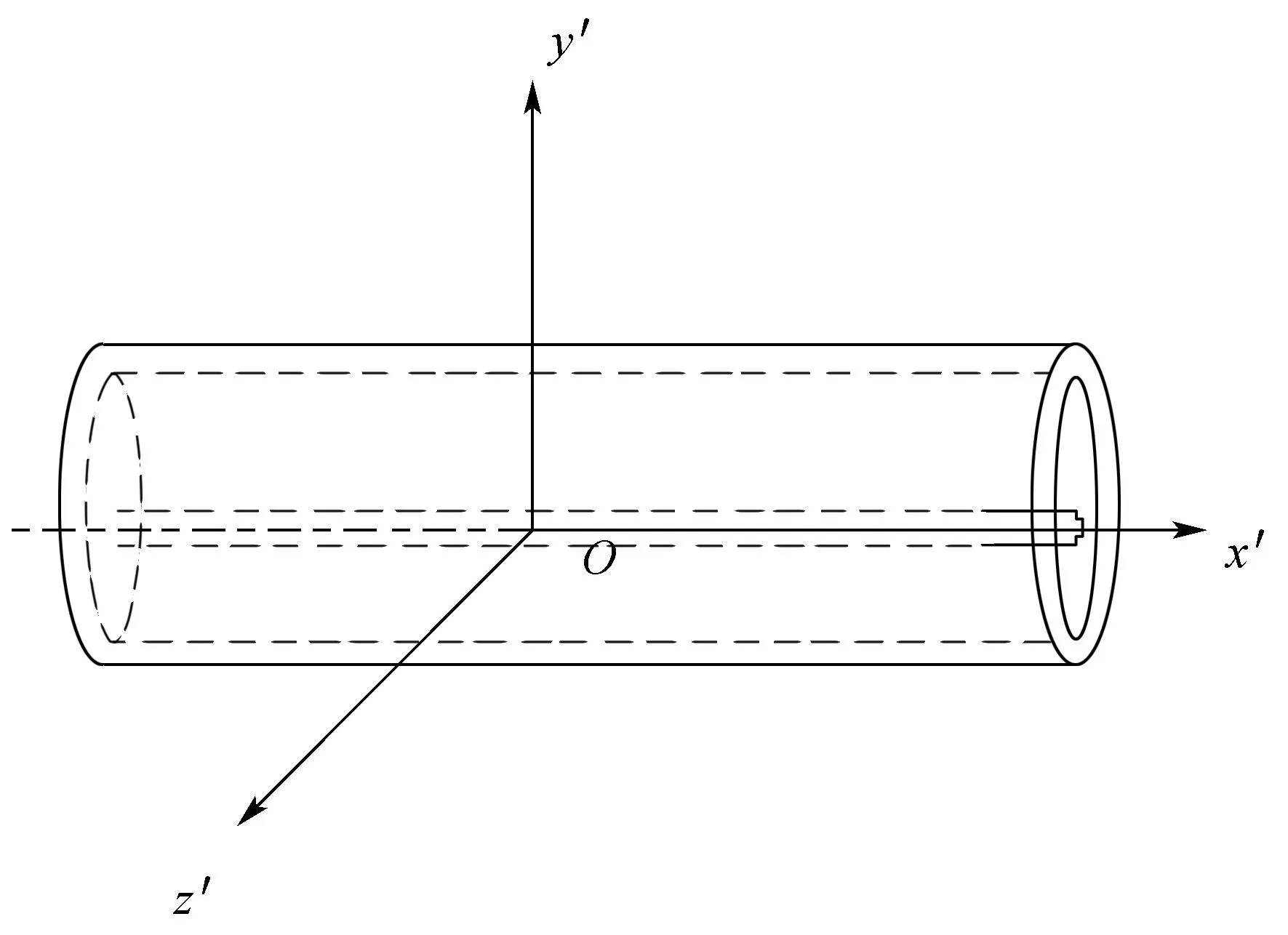
图2　红外石英灯模型示意图Fig.2　Schematic for the model of quartz lamp

石英灯主要包括两个部分：灯丝与灯管.由于忽略两端的影响，在形体上灯管用直管描述，而灯丝简化为一个圆柱体，如图2所示. 现实中，灯丝是呈螺旋状旋绕的细钨丝，比较复杂，但相对于灯箱内部腔体，灯丝形体纤细，其辐射行为可以与一定直径的圆柱体等效.

石英的辐射属性与辐射的波长密切相关，通常对于0.2～4.0 μm波段的辐射，石英可以看成是透明的，而这个波段之外的热辐射则几乎不透明[8]. 因此，本文模型中的能量粒子按照一定的分布赋予了波长属性，根据能量粒子的波长，决定了能量粒子在入射石英灯管之后的行为. 如果能量粒子处于不透明的波段，那么它将被吸收或反射；而能量粒子处于透明波段，则可能发生折射. 这取决于入射角、波长以及石英的光学属性. 对于石英灯管表面的反射率ρ(θi)，其具体的数学描述[9]为：

(1)

其中：

2a2=[(η2-κ2-sin2θi)2+4η2κ2]1/2+

(η2-κ2-sin2θi)

2b2=[(η2-κ2-sin2θi)2+4η2κ2]1/2-

(η2-κ2-sin2θi)

θi为入射角. 对于气体-石英界面:

η=ηq， κ=κq

而对于石英-气体界面:

其中：ηq和κq分别为石英的复数折射率的实部和虚部.ηq和κq取决于能量粒子的波长，其数据可以查表获得.

对于石英灯管表面的折射轨迹，其数学描述[10]为

(2)

其中：φ为折射角；θi为入射角.

1.3统计与计算

本文模型中，须跟踪发射的能量粒子，直到它被吸收或者到达试样表面. 由于本文需分析试样表面入射的辐射热通量分布，因此对试样表面区域进行网格划分，统计网格内接收到的能量粒子数n，可以按式(3)计算辐射热通量(q).

(3)

其中：Qt为RPP仪内部所有热辐射源发出的能量总和；N为热源发出的能量粒子数总和；A为试样表面的某个网格面积.

2验证实验

验证实验采用一台美国Richmond 公司生产的RPP仪，这台仪器基本根据ASTM F2702标准[11]设计，但少数几个地方略有不同：隔热板窗口的上边缘比标准略高8mm，灯管的发光长度约为178mm，而不是标准中的127mm，灯管间距约1mm，而不是标准中的0.4mm. 由于本文探讨的对象是RPP仪产生的辐射热通量(即试样表面的入射辐射热通量)，而不是通过试样的热通量. 因此，在进行验证实验时，直接暴露热通量传感器以检测所在位置的辐射热通量，而不加载任何试样. 通过移动热通量传感器的位置，获得不同位置的辐射热通量分布. 热通量传感器直接采用RPP仪自带的铜片热通量传感器，其探测区域是直径为4cm的圆盘外形，它所测得的热通量值实际上是圆盘区域的平均值. 石英灯管壁和灯箱内壁的温度采用红外热像仪(FLIR T440, FLIR System Inc, 美国)进行测量.

数值模型采用面向对象的Visual C++进行编程实现，运行在一台工作站 (Dell Precision T5610, 美国)上，配置有两个6核CPU(Intel®Xeon®CPU E5—2620@2.10 GHz).采用20个线程进行并行计算以提升计算速度. 验证模型采用的几何参数根据仪器的实际尺寸进行设置，也就是除了少数尺寸与标准不同外，其他都可以从ASTM F2702中获得. 辐射属性参数如表1所示.模型中呈螺旋状的钨丝采用圆柱体进行表示，其直径需要确定，在此直径下，其辐射效果与螺旋状钨丝相当. 当直径配置为1.2mm时，中心区域的辐射热通量给出合理的结果，因此，这个圆柱体的直径被设置为1.2mm.

验证模型中，最终接收能量粒子的物体不是试样，而是热通量传感器的探测表面，在统计时仍然采用式(3)，但这时A为热通量传感器的探测区域的面积，而不是网格面积.

表1　模型中的辐射属性参数

3计算结果与分析

为了便于阐述，以试样夹板1外表面的中心点为原点，建立如图3所示的直角坐标系.

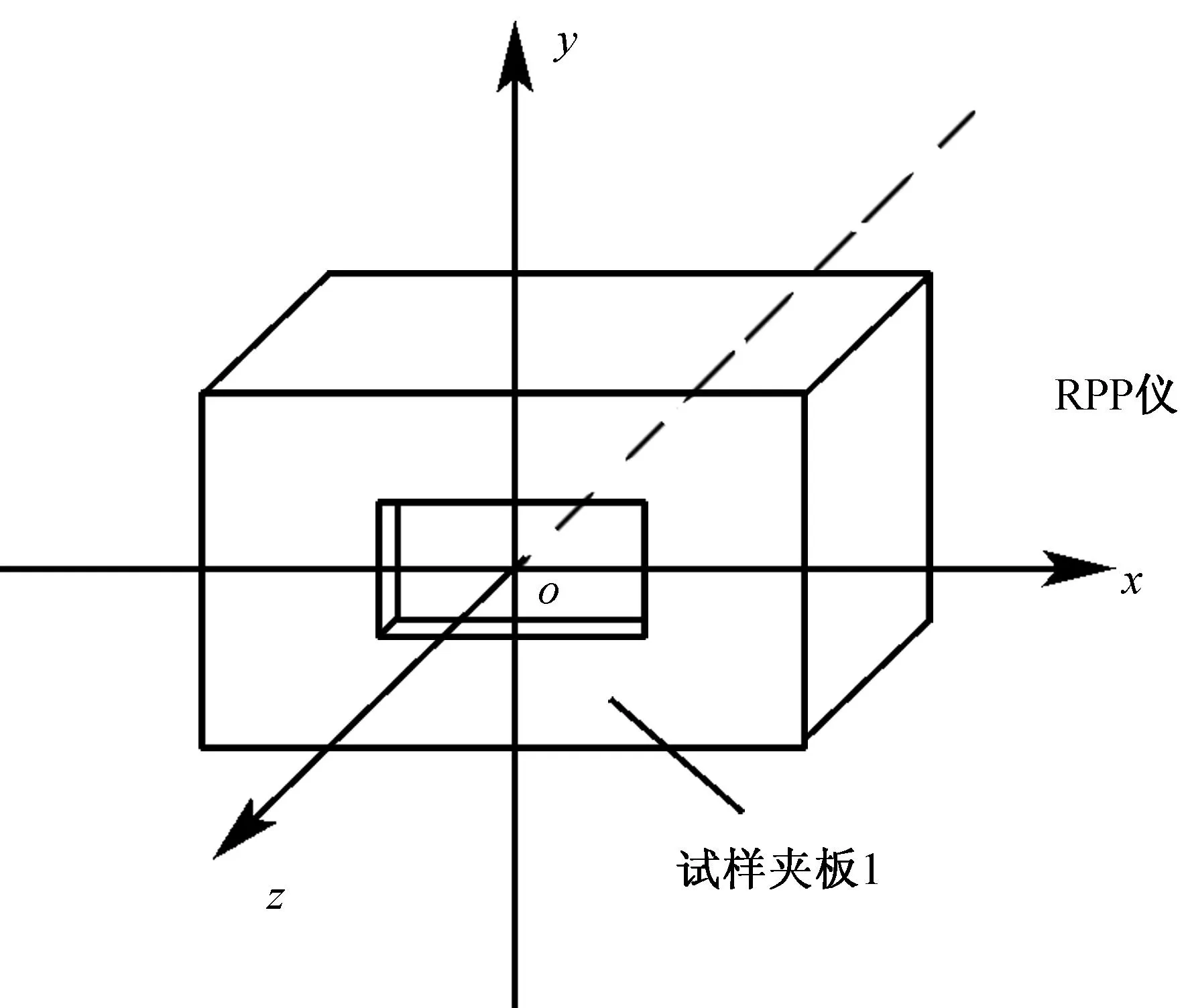
图3　RPP仪的直角坐标系统示意图Fig.3　Cartesian coordinate system in 　the RPP apparatus

通过建立的验证模型，在中心区域辐射热通量为21 kW/m2的情形下计算了在x轴与y轴上的辐射热通量分布，此时灯管、灯箱内壁、挡板室以及试样夹板1的温度测量结果分别为894， 556， 370和298K. 灯丝的温度则依据文献 [1]的实验结果设为1625K. 由于以传感器探测区域为能量粒子接收面，统计区域相对较大，发射106个能量粒子，辐射热通量计算结果已经稳定. 在x轴与y轴上的辐射热通量分布测试及计算结果如图4所示.由图4(a)表明，在x= [-20mm, 20mm] 区间的辐射热通量分布较为均匀，而且处于相对高的热通量范围，而在这个区间之外，距离原点越远，辐射热通量衰减越快.由图4(b)表明，在y= [-10mm, 10mm] 区间的辐射热通量分布较均匀.由图4可以看出，测试结果与理论计算结果比较吻合，证明了模型的合理性与正确性.

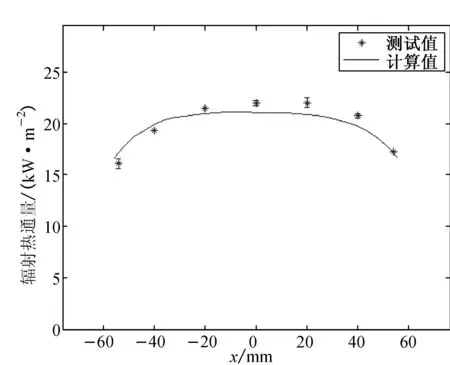
(a)

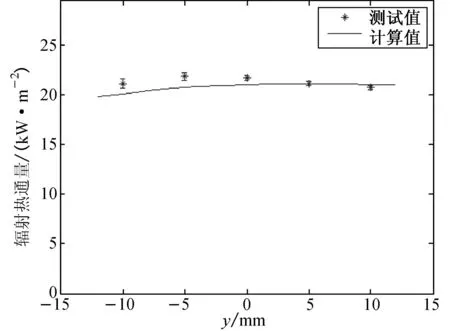
(b)图4　在x轴和y轴上的辐射热通量分布Fig.4　Distribution of the heat flux on x and y axis

在模型得以验证之后，为了更加精细地分析试样表面入射的辐射分布，对试样接收面(与试样夹板1窗口一样大小，尺寸为152 mm × 64 mm)划分152×64个网格. 统计每个网格上接收到的能量粒子，计算每个网格上的辐射热通量值，从而获得辐射热通量分布. 由于本文的研究对象是标准的RPP仪，因此，此时建立模型的几何参数完全按照ASTM F2702进行设置，而不再按照验证仪器的实际尺寸. 此时计算的情形同样是中心区域辐射热通量为21 kW/m2. 通过发射1010个能量粒子，最终得到的结果如图5所示. 图5中的每个点颜色对应相应坐标下的热通量值. 图5中辐射热通量值在空间上的波动源于蒙特卡罗法的统计学特性，但事实上这些波动很小(CV值<0.6%)，并不影响所要求的精度.图5清晰地呈现了辐射热通量以坐标原点为中心的椭圆形分布，离中心越远，椭圆上的辐射热通量值越小. 除边缘部分的辐射热通量相对较低之外，内部的热通量分布相对均匀，这与实验中观察到试样烧伤部位集中在中心区域的现象一致. 注意到在图5中热通量值的分布梯度比图4中大，原因是前者为非常小的网格(1 mm × 1 mm)上的热通量平均值，而后者为直径4cm的圆形区域上的平均值，因此，后者要平缓得多.

图5　xOy平面上的辐射热通量分布

4结语

本文采用蒙特卡罗法对辐射热防护测试(RPP)仪进行数值分析，计算结果表明，在试样的入射表面，辐射热通量分布并不均匀，高热通量集中分布在内部的椭圆形区域. 尽管RPP仪测试中传感器所检测的中心区域部分辐射热通量分布相对均匀，本文所建立的模型对于RPP仪的改进可以提供重要的理论支持.

参考文献

[1] KELTNER N R. Evaluating thermal protective performance testing [J]. Journal of the ASTM International , 2005(2):191-204.

[2] NFPA 1977—2005 Protective clothing and equipment for wildland fire fighting [S]. Quincy, MA: National Fire Protection Association, 2005.

[3] STOLL A M, GREENE L C. Relationship between pain and tissue damage due to thermal radiation [J]. Journal of Applied Physiology, 1959,14(3): 373-382.

[4] STOLL A M, CHIANTA M A. Method and rating system for evaluation of thermal protection [J]. Aerospace Medicine, 1969,40(11):1232-1238.

[5] HOWELL J R. Thermal radiation heat transfer [M]. 4th ed. New York: Taylor and Francis, 2010.

[6] MODEST M F. Radiative heat transfer [M]. 2nd ed. Oxford: Academic Press, 2003.

[7] 刘伟.辐射介质传热[M].北京：中国电力出版社,2009.

[8] WENTINK T, PIANET W G. Infrared emission spectra of quartz [J]. Journal of the Optical Society of America, 1961,51(6):595-600.

[9] TOULOUKIAN Y S, DEWITT D P. Thermal radiative properties-nonmetallic solids [M]. New York: Plenum Press, 1972.

[10] OZISIK M N. Radiative transfer and interactions with conduction and convection [M]. Hoboken, NJ: John Wiley & Sons, Inc, 1980.

[11] ASTM F2702—2015 Standard test method for radiant heat performance of flame resistant clothing materials with burn injury prediction [S].

[12] TURNER T L, ASH R L. Numerical and experimental analyses by of the radiant heat produce produced by quartz heating systems [R]. NASA Technical Paper, 1994:3387.

Numerical Analysis of a Radiant Protective Performance Apparatus Based on the Monte Carlo Method

WANXian-fu1, 2，WANGJun2，HUANGWei2

(1. Zhejiang Provincial Key Laboratory of Novel Textiles Research and Development, Hangzhou 310001, China;2. College of Textiles, Donghua University, Shanghai 201620, China)

Abstract:In order to analyze the radiant heat flux distribution at the incident surface of test specimen in radiant protective performance(RPP) apparatus, a numerical model based on the Monte Carlo method was developed. And experiments were conducted to validate the model. It is found that the predictions of the model show a good agreement with the experimental results. Further, at the incident surface of the sample, the calculation results show an oval-shaped distributed heat flux area with a high energy concentrated in the interior region. The radiant heat flux distribution is relatively uniform at the central region, and relatively low on both sides of the edge. The results will provide a theoretical guideline for further research on the protective effect of the specimen in RPP testing.

Key words:radiative heat transfer；radiant protective performance；radiant heat flux；Monte Carlo method

中图分类号：TK 121

文献标志码：A

作者简介：万贤福(1979—)，男，江西赣州人，副教授，博士，研究方向为服装热湿舒适性.E-mail: wanxianfu@hotmail.com

基金项目：国家自然科学基金资助项目(51106021)；浙江省公益基金资助项目(2013C31006)

收稿日期：2014-11-14

文章编号：1671-0444(2016)01-0063-04