震后多品种应急物资多级配送中的选址-路径模型*

杨恩缘，李　进，严翌娴，黄文耀

(浙江工商大学 计算机与信息工程学院，浙江 杭州 310018)



震后多品种应急物资多级配送中的选址-路径模型*

杨恩缘，李进，严翌娴，黄文耀

(浙江工商大学 计算机与信息工程学院，浙江 杭州 310018)

摘要:地震发生后的应急物资配送是地震救援工作开展的关键。震后应急物资配送往往需要建立多级应急物流中心和规划物流中心间的配送路径，而且应急物资的需求具有多样性。基于这些特点，以总运输成本最小为目标，考虑应急物流中心的容量限制以及应急物资配送的多级性和多样性，建立了震后多品种应急物资多级配送选址-路径问题的混合整数规划模型。该模型选择由供应点、物资集散地、配送中心和需求点构成的多级配送网络，将帐篷、食物和药物作为应急救援物资。最后，采用一个汶川地震中物资配送的实例验证了模型的有效性和可行性。

关键词:地震；应急物流；选址-路径问题；多级配送；汶川地震

近年来，我国大大小小的地震频繁发生，如2008年的汶川8.0级大地震、2010年的玉树7.1级地震、2013的芦山7.0级地震、2014年的云南鲁甸6.5级地震等，都给人类的生存和社会的进步构成了巨大威胁。中国地震台监测结果显示，2014年全年，我国及沿岸近海3级以上地震共703次，其中3.0~3.9级552次，4.0~4.9级121次，5.0~5.9级24次，6.0~6.9级5次，7.0级以上1次，2014年震级最大的是2月12日新疆于田7.3级地震，灾害损失最严重的是云南鲁甸6.5级地震，该地震共造成了600多人死亡、3 000多人受伤，直接经济损失超过了200亿元。

地震灾害发生后，救援物资的需求在一段时间内呈指数增长，供应是否快速充足直接关系到救援的成效。那么，震后应急救援物资如何及时地供给和调度，物流设施如何定位，运输路径如何规划，这些问题都是抗震救灾工作需要研究的课题。

许多学者研究了震后应急物流配送问题。陈刚等[1]分析了3层结构的震后应急物资敏捷保障体系，建立以时间最短的应急物资配送模型，对物资的运输路径及配送方案进行优化求解。在应急物流中心的定位方面，徐峥岐等[2]建立了一种应急物流配送中心选址问题的混合整数规划模型。马丹祥等[3]建立了多目标选址模型并用粒子群算法对模型进行求解。董银红[4]建立了基于道路拥塞的应急选址双层规划模型，并设计了隐枚举下降算法，经过决策行为的交互进行，使公共部门和受灾区达到供需的均衡。马祖军等[5]等基于混合整数非线性规划方法建立了一个应急物资配送中转设施选址-联运问题优化模型。

路径决策对于应急救援物资的配送同样十分重要。刘春年等[6]提出了基于路阻函数理论与Dijkstra算法的最优路径数学模型。高鸿鹤等[7]以配送时间最短为目标，建立了应急物流路径优化模型。唐炉亮等[8]构建了从危险区域的多集结点到安全区域的多安置点的多层次应急疏散模型，实现在最短时间内的受灾群众整体最优疏散。李进等[9]以总疏散时间最小为目标，建立了基于路径的网络流控制应急疏散模型，提出了一种快速求解启发式算法。白永秀等[10]提出了一个基于AHP法的应急物资配送路径选择模型，该模型以应急配送总时间最短、总成本最低、受灾地对物流服务满意度最大为影响因素，建立了三个目标函数。詹沙磊等[11]研究了多出救点、多受灾点、多应急物资的应急设施选址与物资配送问题，考虑了需求及配送路径的不确定性，建立了应急物流的多目标随机规划模型。

以上文献多是针对应急设施选址问题和车辆路径问题进行单独解决，但是从应急物流系统整体集成角度，应急设施选址问题和运输路径问题二者是不可分割的，两个问题在解决应急物资配送优化过程中存在相互依赖，相互影响的关系。代颖等[12]综合考虑了定位—路径问题，建立了一个带时间窗限制、存在多种随机情况的应急物流系统中的模糊定位—路径优化模型，设计了一种混合多目标遗传算法予以求解，但是此文研究的只是单品种的应急物资配送。Han等[13]考虑到道路容量和需求时间窗限制，采用拉格朗日松弛法将应急定位-路径综合问题转化为定位和路径单个问题分别进行解决。曾敏刚等[14]建立了定位-路径问题的数学模型，利用最小包络法来分析应急救助中心的定位问题，应用网络层次分析法确定了最优的运输路径。郑斌等[15]等研究了应急物资需求模糊的情况，建立了应急物资需求模糊的多目标优化模型，并采用多目标遗传算法和改进多目标遗传算法求解模型。Alumur等[16]以总成本最小和运输风险最低为目标，建立了多目标选址-路径问题模型。Caballero等[17]以经济成本最小化和社会影响最小化为目标，探讨了一类多目标有容量限制的选址-路径问题。

目前大多数的震后定位-路径问题研究只考虑了大规模灾害发生后的单级配送，不经过中转站即直接从供应点向需求点运输物资。实际上，这样的研究缺乏一定的现实意义。为此，本文考虑了实际地震灾害发生后的多级配送问题，构建一个多品种应急物资多级配送网络。并选取食物、帐篷、药物作为应急物资，分析多品种物资在不同类型应急物流中心之间的分配问题，同时考虑不同需求点的不同物资需求。

1问题描述

1.1问题假设

地震发生后通常需要从震区外围供应点紧急调度多种应急物资，为了使模型的实际应用性更强，本文考虑了三类在震后需求量较大的救援物资：帐篷、食物和药物。在救援过程中，除了选择灾区外围大型场所作为供应点外，还需要在灾区建立若干个物资集散地承担救援物资的中转、存储以及再分配等功能。再由物资集散地将分配好的物资运往各类物资配送中心，最后由配送中心将救援物资送往需求点，如图1所示，模型将构建一个供应点—物资集散地—配送中心—需求点的多品种应急物资多级配送网络。本文所构建的多级配送网络中的物资集散地的位置是待定的，需要根据总运输成本最小的原则选择最合适的位置。

图1　多品种应急物资多级配送网络图

考虑到地震发生后距离震源不同的区域受到破坏的程度不同，将需求点分为临时救助点和受灾点。临时救助点与受灾点的区别在于，临时救助点的房屋因地震破坏而无法居住，因此需要为位于临时救助点的受灾群众提供帐篷作为临时住所，并为其提供食物和药物，而位于受灾点的群众可以住在原有的房屋里，只需要为他们提供食物与药物。需要解决的问题是在考虑应急物流中心容量以及满足需求的情况下确定需要建立的物资集散地的位置并对应急物资的运输路径进行规划，求出相关应急物流中心之间的物资运输数量，以实现总的运输成本最小。

1.2 模型符号、参数和变量

模型符号如下所示。

N=(V,C)：震后应急配送网络中，其中V为节点集合，C为弧集；

I={1,…,x}：物资集散地集合，I∈V；

J={1,…,y}：帐篷配送中心集合，J∈V；

K={1,…,z}：食物配送中心集合，K∈V；

L={1,…,w}：药物配送中心集合，L∈V；

A={1,…,q}：临时救助点集合，A∈V；

B={1,…,r}：受灾点集合，B∈V。

模型参数如下所示。

TC：每单位帐篷每千米的运输成本；

FC：每单位食物每千米的运输成本；

DC：每单位药物每千米的运输成本；

TS：从供应点供应的帐篷数量上限；

FS：从供应点供应的食物数量上限；

DS：从供应点供应的药物数量上限；

DN：可以建立的物资集散地的数量上限；

MRi：物资集散地i的容量，i∈I；

TRj：帐篷配送中心j的容量，j∈J；

FRk：食物配送中心k的容量，k∈K；

DRl：药物配送中心l的容量，l∈L；

TDa：临时救助点a的帐篷需求，a∈A；

FDIa：临时救助点a的食物需求，a∈A；

DDIa：临时救助点a的药物需求，a∈A；

FD2b：受灾点b的食物需求，b∈B；

DD2b：受灾点b的药物需求，b∈B；

D1i：供应点到物资集散地i的距离，i∈I；

D2ij：物资集散地i到帐篷配送中心j的距离，i∈I，j∈J；

D3ik：物资集散地i到食物配送中心k的距离，i∈I，k∈K；

D4il：物资集散地i到药物配送中心l的距离，i∈I，l∈L；

D5ja：帐篷配送中心j到临时救助点a的距离，j∈J，a∈A；

D6ka：食物配送中心k到临时救助点a的距离，k∈K，a∈A；

D7kb：食物配送中心k到受灾点b的距离，k∈K，b∈B；

D8la：药物配送中心l到临时救助点a的距离，l∈L，a∈A；

D9lb：药物配送中心l到受灾点b的距离，l∈L，b∈B。

决策变量如下所示。

VT1i：从供应点运往物资集散地i的帐篷数量，i∈I；

VF1i：从供应点运往物资集散地i的食物数量，i∈I；

VD1i：从供应点运往物资集散地i的药物数量，i∈I；

VT2ij：从物资集散地i运往帐篷配送中心j的帐篷数量，i∈I，j∈J；

VF3ik：从物资集散地i运往食物配送中心k的食物数量，i∈I，k∈K；

VD4il：从物资集散地i运往药物配送中心l的食物数量，i∈I，l∈L；

VT5ja：从帐篷配送中心j运往临时救助点a的帐篷数量，j∈J，a∈A；

VF6ka：从食物配送中心k运往临时救助点a的食物数量，k∈K，a∈A；

VF7kb：从食物配送中心k运往受灾点b的食物数量，k∈K，b∈B；

VD8la：从药物配送中心l运往临时救助点a的药物数量，l∈L，b∈B；

VD9lb：从药物配送中心l运往受灾点b的药物数量，l∈L，b∈B；

Hi：为0~1变量，如果物资集散地i被建立则为1，否则为0，i∈I；

G1ij：为0~1变量，如果由物资集散地i向帐篷配送中心j运送帐篷则为1，否则为0，i∈I，j∈J；

G2ik：为0~1变量，如果由物资集散地i向食物配送中心k运送食物则为1，否则为0，i∈I，k∈K；

G3il：为0~1变量，如果由物资集散地i向药物配送中心l运送药物则为1，否则为0，i∈I，l∈L。

1.3数学模型

(1)

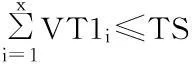
(2)

(3)

(4)

5VT1i+9VF1i+VD1i≤MRi，∀i；

(5)

(6)

(7)

(8)

(9)

(10)

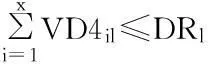
(11)

(12)

(13)

(14)

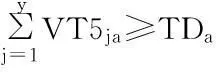
(15)

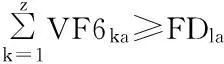
(16)

(17)

(18)

(19)

(20)

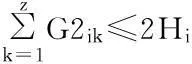
(21)

(22)

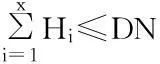
(23)

VT1i；VF1i；VD1i, VT2ij,VF3ik,VD4il,VT5ja,VF6ka,VF7kb,VF7kb,VD8ia,VD9lb≥0;Hi,G1ij,G2ik,G3il∈{0,1};∀i,j,k,l,a,b 。

(24)

其中，目标函数(1)表示应急救援物资从供应点到需求点之间各级物流中心的距离与对应的运输数量之积再乘以运输成本后累加和最小，即总的运输成本最小。式(2)~(4)分别表示从供应点运往物资集散地的各物资(帐篷、食物和药物)数量不超过各物资的供应数量限制；式(5)表示从供应点运往物资集散地的总物资数量不超过物资集散地的容量，物资集散地的容量以药物为单位来表示，将食物以及帐篷按照重量换算成药物单位来表示，本文假设1单位的帐篷等于5单位的药物，1单位的食物等于9单位的药物；式(6)表示从物资集散地运往帐篷配送中心的帐篷数量不超过由供应点运往物资集散地的帐篷数量；式(7)表示从物资集散地运往食物配送中心的食物数量不超过由供应点运往物资集散地的食物数量；式(8)表示从物资集散地运往药物配送中心的药物数量不超过由供应点运往物资集散地的药物数量；式(9)~(11)分别表示从物资集散地运往各配送中心的物资数量不超过配送中心的容量；式(12)表示从帐篷配送中心运往临时救助点的帐篷数量不超过从物资集散地运往帐篷配送中心的帐篷数量；式(13)表示从食物配送中心运往两个需求点(临时救助点和受灾点)的食物数量不超过从物资集散地运往食物配送中心的食物数量。式(14)表示从药物配送中心运往两个需求点(临时救助点和受灾点)的药物数量不超过从物资集散地运往药物配送中心的药物数量；式(15)~(17)分别表示由配送中心运往临时救助点的各物资(帐篷、食物和药物)数量能够满足临时救助点的需求；式(18)和(19)分别表示由配送中心运往受灾点的各物资(食物和药物)数量能够满足受灾点的需求；式(20)~(22)分别确保了只有被建立的物资集散地可以向各配送中心(帐篷、食物和药物)运送物资；式(23)为可以建立的物资集散地的数量约束；式(24)为决策变量的非负约束和0~1约束。

2实例分析

2.1实例数据

以汶川8.0级地震发生后的救援物资配送过程为例，如图2所示，选取成都双流国际机场作为供应点，彭州市的龙门山镇(M1)、通济镇(M2)和小鱼洞镇(M3)作为3个候选物资集散地。其中，龙门山镇距离成都双流国际机场74.2km，通济镇距离成都双流国际机场66.7km，小鱼洞镇距离成都双流国际机场70.8km。另外，选取3个帐篷配送中心(T1，T2,T3),4个食物配送中心(F1,F2,F3,F4)和1个药物配送中心(D1)。表1给出了各应急物流中心的容量限制。表2为候选物资集散地到各配送中心的距离，距离根据百度地图测量得到。

图2　汶川地震中各应急物流中心和需求点的分布图

应急物流中心容量应急物流中心容量龙门山镇M160000食物配送中心F12500通济镇M260000食物配送中心F22000小鱼洞镇M360000食物配送中心F33000帐篷配送中心T1、T3300食物配送中心F43500帐篷配送中心T2500药物配送中心D14000

表2　候选物资集散地到各配送中心的距离

表3　临时救助点的物资需求量

表4　受灾点的物资需求量

假设从成都双流国际机场供应点提供的帐篷、食物和药物数量分别为1 000、10 000和4 000个单位。本文选取9个临时救助点(A1,A2,…,A9)以及19个受灾点(B1,B2,…,B19)作为应急救援物资的需求点。各需求点的物资需求数量是按照人口进行计算的，人口数据是在一般自然村的人口数量基础上随机产生的。假设位于临时救助点的受灾群众都需要帐篷，平均每三个人使用一顶帐篷，每个人都需要一个单位的食物，60%的人需要药物；位于受灾点的受灾群众不需要帐篷，每个人需要一个单位的食物，30%的人需要药物。表3为9个临时救助点的物资需求量，表4为19个受灾点的物资需求量。各配送中心到临时救助点和受灾点的距离来自于百度地图上两点间的直线距离。

对于应急救援物资的运输成本，本文根据目前市场租车的行情以及地震后物流环境的不稳定性，估计应急救援物资的运输成本。假设运输1单位帐篷1km的成本为1.8元，运输1单位食物1km的成本为2.5元，运输1单位药物1km的成本为0.5元。

2.2实例求解

本文采用LINGO15编写了模型的求解程序，利用线性规划以及0~1整数规划的计算思路，得出最优的目标函数值为1 731 560元。表5给出了由成都双流国际机场向三个候选物资集散地运送的物资数量，可以看出需要在通济镇和小鱼洞镇

建立物资集散地，而龙门山镇的帐篷、食物、药物的供应数量均为0，即不需要在龙门山镇建立物资集散地；表6为物资集散地与各配送中心之间的物资运输数量；表7为配送中心与各临时救助点之间的物资运输数量；表8为配送中心与各受灾点之间的物资运输数量。

表5　由供应点运往物资集散地的物资数量

表6　物资集散地与各配送中心之间的物资运输数量

表7　配送中心与各临时救助点之间的物资运输数量

通过以上汶川地震的实例验证了本文建立的震后多品种应急物资多级配送选址-路径模型是有效的和可行的，能够为应急管理部门提供决策支持和参考借鉴。

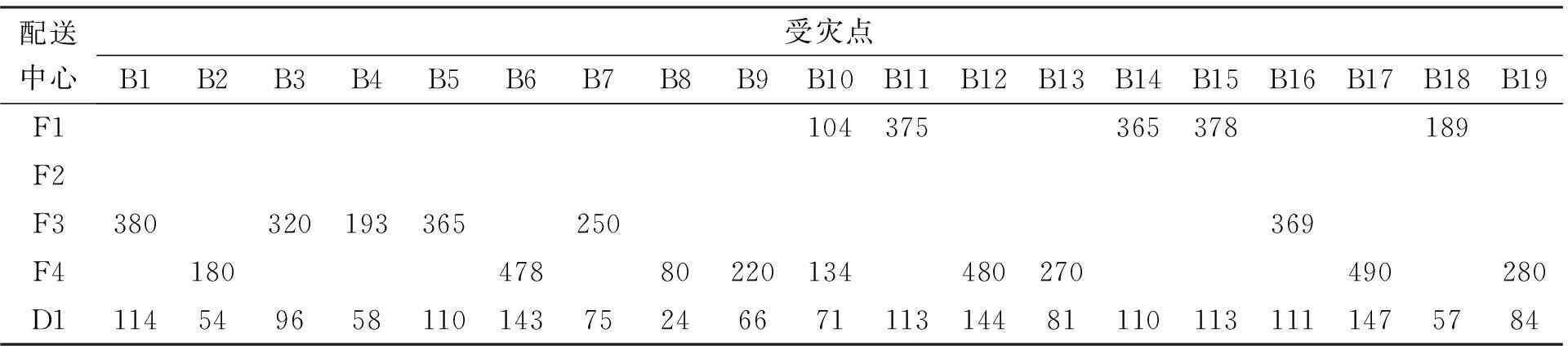
表8　配送中心与各受灾点之间的物资运输数量

3结论

震后应急物资的配送是应急救援能否成功落实的关键，合理地选择应急物资的物流配送中心和运输路径对提高应急救援工作效率具有十分重要的意义。本文综合震后应急救援物资配送中的配送中心选址和运输路径问题，基于震后应急物流配送的特点，不仅考虑了震后物资需求的多样性，同时考虑了不同应急物流中心之间的多级配送。

本文研究了地震发生后维持灾区群众基本生活的应急物资的配送，应急物资包括食物、药物以及帐篷，在供应点到需求点之间还存在着物资集散地以及与多种应急物资对应的配送中心，从而形成了一个多品种应急物资的多级配送网络。在此基础上，本文构建了满足灾区群众需求的以配送成本最小为目标函数的震后多品种应急物资多级配送的选址-路径数学模型，该模型考虑了各个物流中心的容量限制与受灾点的需求，能够得到需要建立的应急物流中心的位置以及确定从供应点到需求点之间的最佳运输路径。最后，结合我国汶川地震应急救援物资的配送过程，验证了所提出的模型能够较好地求解震后多品种应急物资多级配送的选址-路径问题，能够有效地帮助应急管理部门的决策者提供智力支持和参考借鉴。

进一步的研究将同时考虑总成本最小和总时间最短，并考虑多种车辆类型、车辆容量限制等因素建立多目标规划，在此基础上对震后多品种应急物资选址-路径问题进行建模并且研究快速、有效的求解算法。

参考文献：

[1]陈刚, 张锦, 彭永涛. 震后应急物资敏捷保障体系模型及算法[J]. 自然灾害学报, 2013, 22(3): 47-53.

[2]徐峥岐, 张涛, 曾俊伟. 应急物流配送中心选址问题模型研究[J]. 物流科技, 2015, 38(1): 90-93.

[3]马丹祥, 初建宇, 王政, 等. 基于多目标规划的防灾避难场所选址模型[J]. 自然灾害学报, 2015, 23(2): 1-7.

[4]董银红. 道路拥塞条件下的应急物流选址研究[J]. 经济与管理研究, 2014 (4): 48-53.

[5]马祖军, 郑斌, 李双琳. 应急物资配送中带中转设施的选址-联运问题[J]. 管理评论, 2013, 25(10): 166-176.

[6]刘春年, 邓青菁. 应急决策信息系统最优路径研究—基于路阻函数理论及dijkstra算法[J]. 灾害学, 2014, 29(3): 18-23.

[7]高鸿鹤, 唐辰. 基于配送时间最短的应急物流路径规划[J]. 物流工程与管理, 2014, 36(2): 75-78.

[8]唐炉亮, 杨雪, 刘章, 等. 灾害条件下多层次应急疏散模型的构建方法研究[J]. 灾害学, 2015, 30(2): 179-185.

[9]李进, 张江华. 基于路径的网络流控制应急疏散模型与算法[J]. 自然灾害学报, 2012, 21(6): 9-18.

[10]白永秀, 周溪召. 应急物资配送路径选择问题的研究[J]. 物流技术, 2013, 28(31): 89-91.

[11]詹沙磊, 刘南. 基于模糊目标规划的应急物流多目标随机规划模型[J]. 中国机械工程, 2011, 22(23): 2858-2862.

[12]代颖, 马祖军. 应急物流系统中的随机定位—路径问题[J]. 管理科学报, 2012, 21(2): 212-223.

[13]Han YJ, Guan XH, Shi LY. Optimization based method for supply location selection and routing in large-scale emergency material delivery[J]. IEEE Transactions on Automation Science and Engineering, 2011, 8(4): 683-693.

[14]曾敏刚, 崔增收, 余高辉. 基于应急物流的减灾系统LRP研究[J]. 中国管理科学, 2010,18 (2): 75-80.

[15]郑斌, 马祖军, 方涛. 应急物流系统中的模糊多目标定位—路径问题[J]. 系统工程, 2009, 27(8): 21-25.

[16]Alumur S, Kara B. A new model for the hazardous waste location-routing problem[J]. Computers and Operations Research, 2007, 34(5):1406-1423.

[17]Caballero R, Gonzalez M, Guerrero F, et al. Solving a multi-objective location-routing problem with a metaheuristic based on tabu search[J]. European Journal of Operational Research, 2007, 177(3):1751-1763.

Location-routing Model for Post-earthquake Multi-stage Distribution with Multi-type Emergency Supplies

Yang Enyuan, Li Jin, Yan Yixian and Huang Wenyao

(SchoolofComputerandInformationEngineering,ZhejiangGongshangUniversity,Hangzhou310018,China)

Abstract:The emergency supplydistribution for post-earthquakeis the key to earthquake relief work. It is necessary for post-earthquake emergency supply distribution to build multi-stage emergency logistics centers and determine the distribution routesamong logistics centers. In addition, the demand for emergency supplies isdiversification. Based on these characteristics, minimizing the total transportation cost and considering the capacity constraints of emergency logistics centers and multi-stage and diversification of emergency supply distribution, we establishe a mixed interger programming model for location-routing problem of post-earthquake multi-stage distribution with multi-type emergency supplies. This model chooses the supply places, material centers, distribution centers and demand places as components of multi-stage distribution network, and regards the tents, food and drugs as emergency relief supplies. Finally, a supply distribution example in Wenchuan Earthquake to show the effecitveness and feasibility of the proposed model.

Key words:earthquake; emergency logistics; location-routing problem; multi-stage distribution; Wenchuan Earthquake

doi:10.3969/j.issn.1000-811X.2016.02.038

中图分类号：X43; F252; O221.4

文献标志码：A

文章编号：1000-811X(2016)02-0200-06

作者简介：杨恩缘(1995-)，女，浙江嘉兴人，本科生，主要从事应急管理、系统建模与仿真等方面的研究.E-mail:yangenyuan@163.com通讯作者：李进(1980-)，男，浙江杭州人，副教授，博士，主要从事应急管理、系统建模与仿真等方面的研究.E-mail: jinli@mail.zjgsu.edu.cn

*收稿日期：2015-10-19修回日期：2015-12-04基金项目：国家自然科学基金资助项目(71302035)；浙江省公益性技术应用研究计划项目(2013C33030)

杨恩缘，李进，严翌娴,等. 震后多品种应急物资多级配送中的选址-路径模型[J].灾害学, 2016,31(3):200-205.[ Yang Enyuan, Li Jin, Yan Yixian, et al. Location-routing Model for Post-earthquake Multi-stage Distribution with Multi-type Emergency Supplies[J].Journal of Catastrophology, 2016,31(3)：200-205.]