基于模糊综合评价法的泥石流风险评价*

沈　简，饶　军，傅旭东

(武汉大学 土木建筑工程学院，湖北 武汉 430072)



基于模糊综合评价法的泥石流风险评价*

沈简，饶军，傅旭东

(武汉大学 土木建筑工程学院，湖北 武汉 430072)

摘要:在既有的泥石流危险度模糊综合评价模型中加入易损度因子，首次建立了泥石流风险度模糊综合评价模型，使用该模型对神农架林区内的5条泥石流沟进行风险评价，得出了“模糊综合评价模型可用于泥石流风险评价”的结论。针对“模糊综合评价模型的计算结果能反映风险大小，不能表现风险特点”的问题，将模糊综合评价法与平面坐标相结合，提出一种新的泥石流风险评价法：模糊坐标法。该方法对泥石流的危险度及易损度分别进行模糊综合评价，用评价结果组成坐标点，并定义坐标点到原点的距离为风险度，利用平面坐标的二维属性使得评价结果既能表现危险度又能表现易损度，泥石流风险的具体特点也得以表达。将两种方法的计算结果进行比较分析，得出“模糊坐标法的评价结果更符合实际，模糊综合评价法的计算结果偏安全”的结论。

关键词:模糊综合评价；泥石流；风险评价；模糊坐标；评价因子

我国山体约占领土面积的三分之二，泥石流成为主要地质灾害之一，由国土资源部公布的全国地质灾害通报可知，2008-2012年泥石流灾害造成的经济损失总计44.7亿元。为减轻泥石流灾害造成的损失，保护国家和人民生命财产安全，需对泥石流灾害进行科学合理地防治。泥石流风险评价是一项防灾减灾的非工程措施，能有效地反映泥石流现在所处的状态以及未来的发展趋势，为科学地组织实施防灾减灾提供一定的理论依据，对泥石流减灾规划、灾区经济建设等具有指导意义。

泥石流风险评价需考虑危险度和易损度[1]，危险度指泥石流沟产生灾害的概率，易损度指泥石流灾害给人民的生命财产以及社会带来的损失程度。基于模糊数学的综合评价模型具有建模简单、易于掌握，对多因素、多层次的复杂问题评价效果好的特点，许多学者将其应用于泥石流灾害评价中。目前，国内学者建立的泥石流模糊综合评价模型皆是危险度评价模型[2-6]，即模型的评价因子为危险度因子，计算时未考虑易损度，不能用于泥石流风险评价。因此，本文对国内外学者建立泥石流危险度评价模型时使用因子的频率进行统计，选取了8个广泛使用的危险度因子，结合实际调查资料，选取了2个易损度因子，首次建立了泥石流风险度模糊综合评价模型。

此外，模糊综合评价模型得到的结果是一个简单数值，仅能反映风险的大小，并不能表现某个泥石流风险的具体特点，为防灾减灾的决策提供更详细的信息。例如，有两条泥石流沟：一条产生灾害的概率小，但附近居民密集、有交通要道，发生灾害造成的损失大；一条产生灾害的概率大，但附近居民稀少、无交通要道，发生灾害造成的损失小。两者的风险度很有可能大小相同，但其对应的防灾减灾工程措施明显不同。针对这一问题，本文将模糊综合评价法与平面坐标相结合，提出一种新的泥石流风险评价法：模糊坐标法。该方法将平面坐标的两个轴定义为危险度和易损度，分别对泥石流的危险度和易损度进行模糊综合评价，用评价结果组成平面坐标，并将该坐标点到原点的距离定义为风险大小。该方法利用平面坐标的二维属性使得评价结果既能表现危险度又能表现易损度，泥石流风险的具体特点也得以表达。

综上所述，本文首次建立了泥石流风险度模糊综合评价模型，并提出了一种新的泥石流风险评价法：模糊坐标法。以神农架林区的5条泥石流沟为例，使用以上两种方法对其进行风险评价。

1模糊综合评价原理

所谓模糊综合评价，就是应用模糊变换原理和最大隶属原则，对多因素影响的事物或现象进行总的评价[7]，其原理简述如下。

设有两个论域：因子集U={u1,u2, …,un}(ui为评价因子)；评价集V={v1,v2, …,vm}(vj为评价等级)。

对U中的每一个因子ui做单因子评价f(ui)，则隶属函数f可以看作是从U~V的模糊映射，通过映射，可以推导出模糊矩阵R：

R=(rij)n×m, 0≤rij≤1 。

(1)

式中：rij表示因子集U中因子ui对应评价集V中等级vj的隶属度。

若存在一个集合U上的模糊子集A={a1, a2, …, an}，A以向量表示，且有：

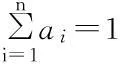
(2)

式中：ai为第i个因子的权重，则可确定U~V的模糊变换B，B为模糊合成结果：

B=A°R。

(3)

记B={b1,b2, …,bm}，其中bj表示被评价事物或现象对应评价等级vj的隶属度。

根据最大隶属原则，如果：

bj0=max{bj:1≤j≤m} 。

(4)

则等级vj0就是最终评价结果对应的等级。

2泥石流风险度的模糊综合评价模型

2.1建立评价因子集U

泥石流风险评价需考虑危险度和易损度，评价因子可分为危险度因子和易损度因子两类。

首先确定危险度因子，统计Akgun[8]、王春磊[9]、Chang[10]等20多个学者建立泥石流危险度评价模型时使用因子的频率，结果见图1(出现次数少于4的因子未在图1中绘出)。图中a为主沟纵坡降，b为流域相对高差，c为24 h最大降雨量，d为松散固体物质储量，e为流域面积，f为植

被覆盖率，g为主沟长度，h为沟谷形态，i为一次最大冲出量，j为岩性，k为爆发频率，l为流域切割密度。

由图1可知，主沟纵坡降、流域相对高差、24 h最大降雨量、松散固体物质储量、流域面积及植被覆盖率是广泛使用的评判因子。

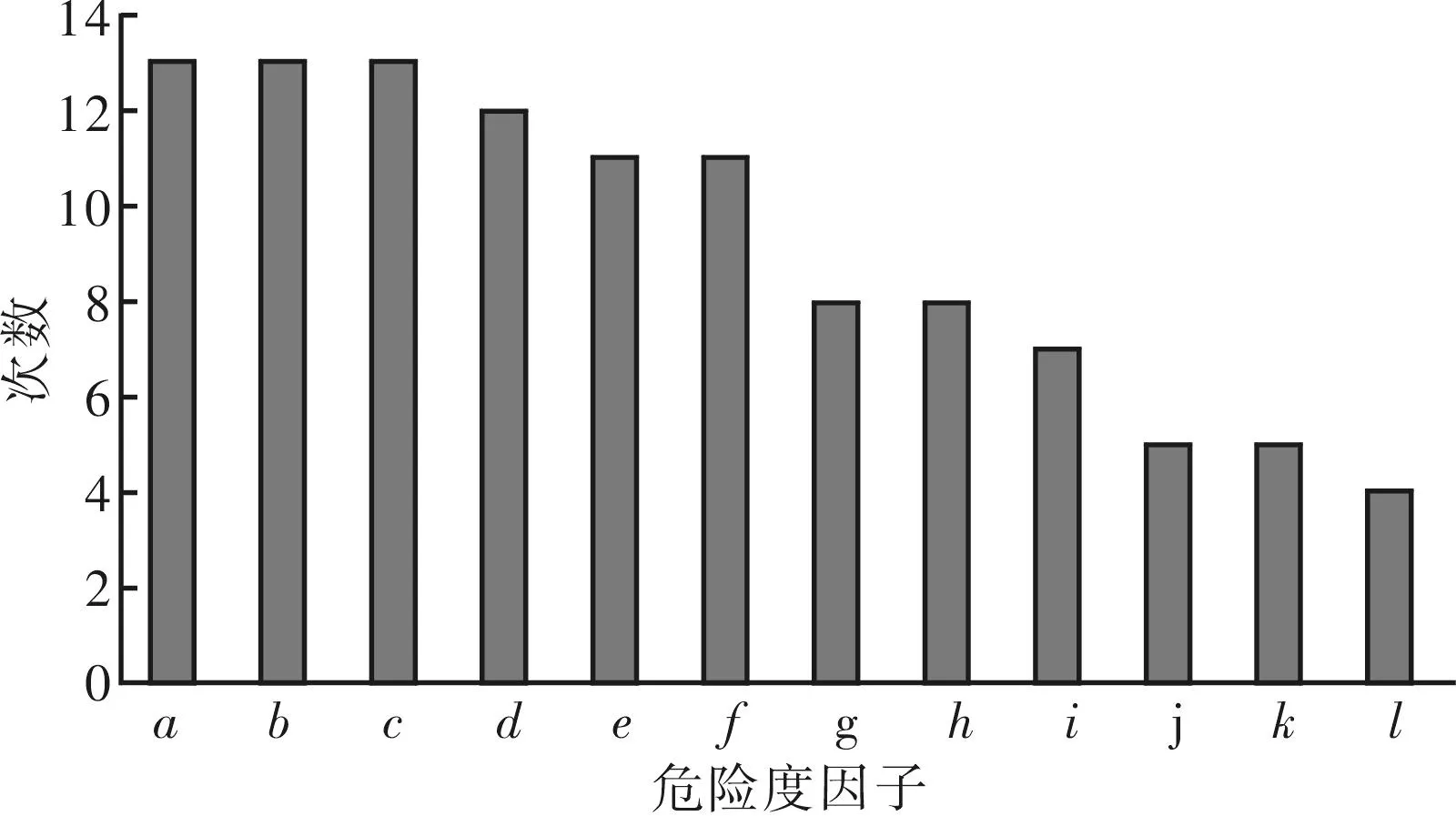
图1　泥石流危险度因子使用频率

根据统计结果，结合泥石流的成因[11-12]和已有的泥石流调查资料，确定危险度因子：一次最大冲出量、流域面积、主沟长度、流域相对高差、主沟纵坡降、松散固体物质储量、日最大降雨量、植被覆盖率。

基于已有的泥石流调查资料，确定易损度因子：威胁人数、预计经济损失。

由于影响泥石流风险度的因子多、类型不同，一级评价模型的权重分配难以做到合理，本文建立二级模糊综合评价模型。用上述10个影响泥石流风险度的因子构成2个一级因子集：

C1= {D1,D2,D3,D4,D5,D6,D7,D8}；

(5)

C2= {E1,E2} 。

(6)

式中：C1中为危险度因子，C2中为易损度因子。2个一级因子集构成二级因子集：

U= {C1,C2} 。

(7)

2.2建立评价集V

根据地质灾害分级分类标准[13]，划分泥石流风险度评价集：

V={轻度(Ⅰ)，中度(Ⅱ)，高度(Ⅲ)，极度(Ⅳ)} 。

(8)

综合多个学者的研究成果，并结合实际调查资料进行分析，将10个评价因子进行分级，见表1。

已知因子集U及评价集V，可构建二级模糊综合评价模型的层次结构图，见图2。

表1　风险度分级标准及评价因子

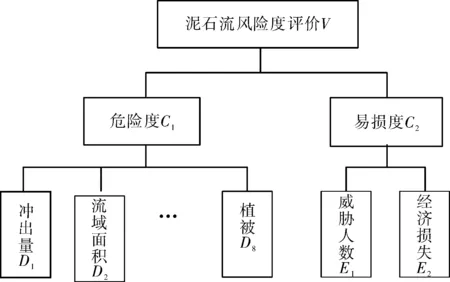
图2　模型层次结构图

2.3隶属函数的确定

因子隶属度的描述是模糊综合评判的关键，隶属度可以通过建立隶属函数，代入实测值计算得到。基于因子数据的分布特征，参考相关学者的使用经验，建立“梯形分布”函数，其公式如下：

(9)

(10)

(11)

(12)

式中：x为评价因子的实测值，s1、s2及s3为表1中的各因子分界值，r1、r2、r3及r4为因子对应各评价等级的隶属度。

2.4权重计算

评价因子权重大小反映了各个因子的重要性及其对风险度的影响程度，对模糊综合评价结果有直接的影响。本文采用AHP层次分析法[14]计算各因子权重，该方法将数学模型与专家的经验判断完美结合，是应用最广泛的权重计算方法之一。按图2的结构层次进行权重计算，其中特征根和特征向量采用和法计算，计算结果见表2。

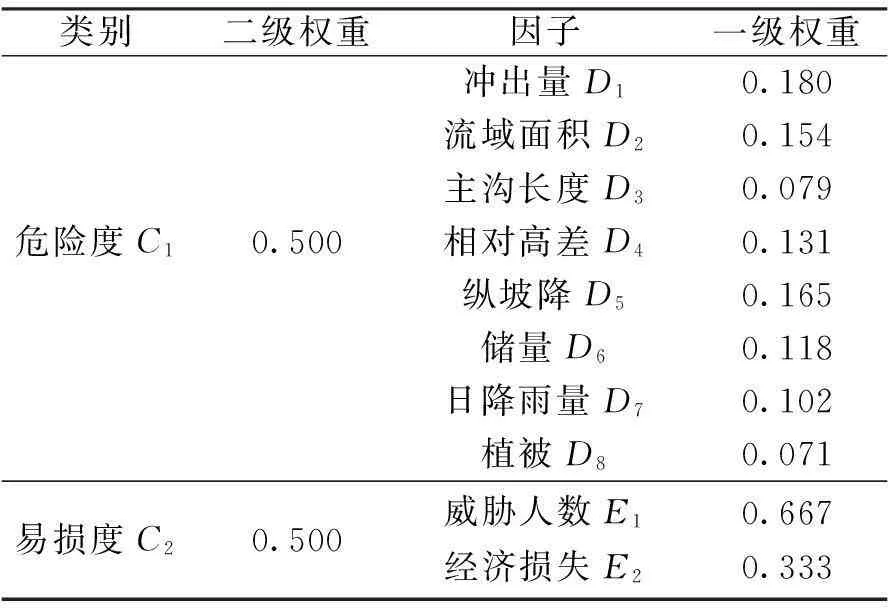
表2　评价因子权重值

综上，确定了因子集、评价集、隶属函数及因子权重，泥石流风险度的模糊综合评价模型已建立。

3应用实例

神农架林区处于地质灾害高发区，泥石流是其中典型的地灾隐患，严重威胁着人民生命财产安全，给城镇规划带来严重困扰，阻碍社会经济可持续发展。进行泥石流沟谷风险度评价，指导灾区建设已成为必不可少的工作之一。在国家科技支撑计划的资助下，作者和本项目有关人员多次赴神农架林区进行资料收集及现场踏勘，取得了与泥石流沟有关的资料。

神农架林区松柏镇、红坪镇、阳日镇、下谷坪四个镇内的5条泥石流沟基本数据见表3。

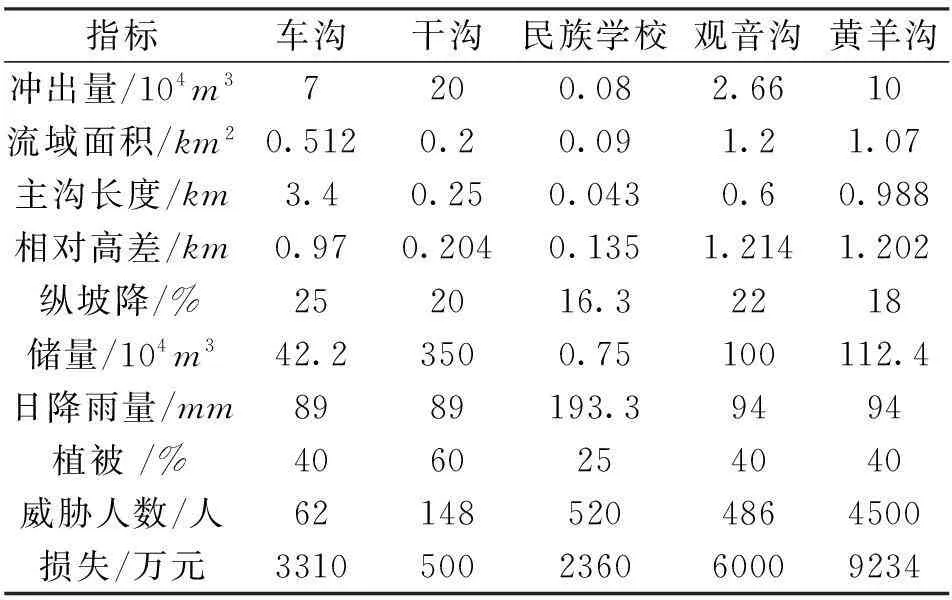
表3　泥石流数据

依据前文建立的泥石流风险度模糊综合评价模型对各泥石流沟进行风险评价，计算结果见表4。

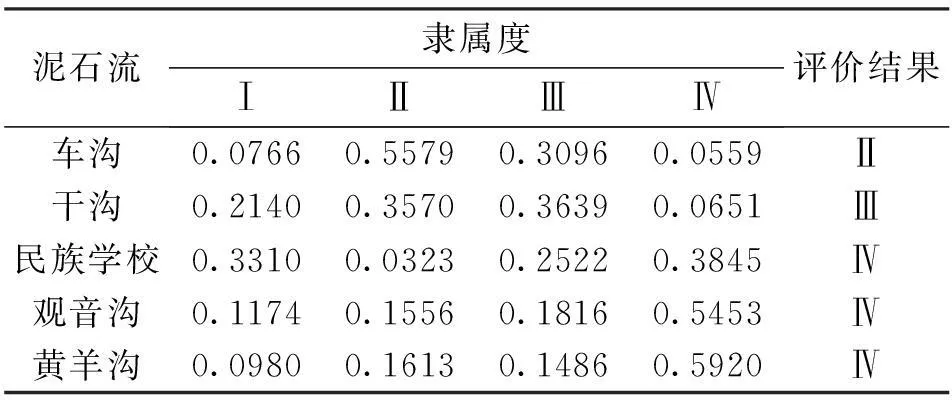
表4　计算结果

由计算结果可知，车沟泥石流具有中度风险，干沟泥石流具有高度风险，民族学校泥石流具有极度风险，观音沟泥石流具有极度风险，黄羊沟泥石流具有极度风险。

4模糊坐标法

对于两条泥石流沟，虽然一条危险度大、易损度小，一条危险度小、易损度大，但模糊综合评价模型的评价结果很有可能是相同的。这说明模糊综合评价模型的计算结果能反映泥石流风险的大小，但不能表现泥石流风险的具体特点。为了让风险评价结果为防灾减灾的决策提供更详细的信息，本文将对模糊综合评价模型与平面坐标相结合，提出一种新的泥石流风险评价法：模糊坐标法。

4.1模糊坐标法原理

(1)危险度、易损度模糊综合评价

建立危险度的因子集Uh、评价集Vh，易损度的因子集合Uv、评价集Vv：

Uh= {D1, D2, D3, D4, D5, D6, D7, D8}；

(13)

Vh={轻度(Ⅰ)，中度(Ⅱ)，高度(Ⅲ)，极度(Ⅳ}；

(14)

Uv= {E1, E2}；

(15)

Vv={轻度(Ⅰ)，中度(Ⅱ)，高度(Ⅲ)，极度(Ⅳ)} 。

(16)

式中：D1~D8和E1~E2对应的因子含义见表2。

已知因子集、评价集，结合前文建立的隶属函数与权重，可对泥石流的危险度及易损度分别进行模糊综合评价。

(2)构建模糊坐标系进行风险评价

建立平面直角坐标系，将横轴定义为危险度，纵轴定义为易损度，危险度及易损度沿坐标轴方向增大，将坐标轴分别命名为危险度和易损度。横纵坐标轴刻度1、2、3、4对应危险度及易损度的评价等级Ⅰ、Ⅱ、Ⅲ、Ⅳ，由泥石流危险度及易损度的评价结果可确定唯一坐标点：

R(H,V) 。

(17)

式中：H为危险度评价结果，V为易损度评价结果。

将坐标点到原点的距离定义为风险度R(Risk)，则得到风险度计算公式：

(18)

根据坐标点到原点的距离大小对泥石流的风险度进行分级，分级标准为：轻度风险04.243。模糊坐标系见图3。

4.2实例计算

按上述原理，用模糊坐标法对5条泥石流沟进行风险度评价，计算结果见表5、图4。

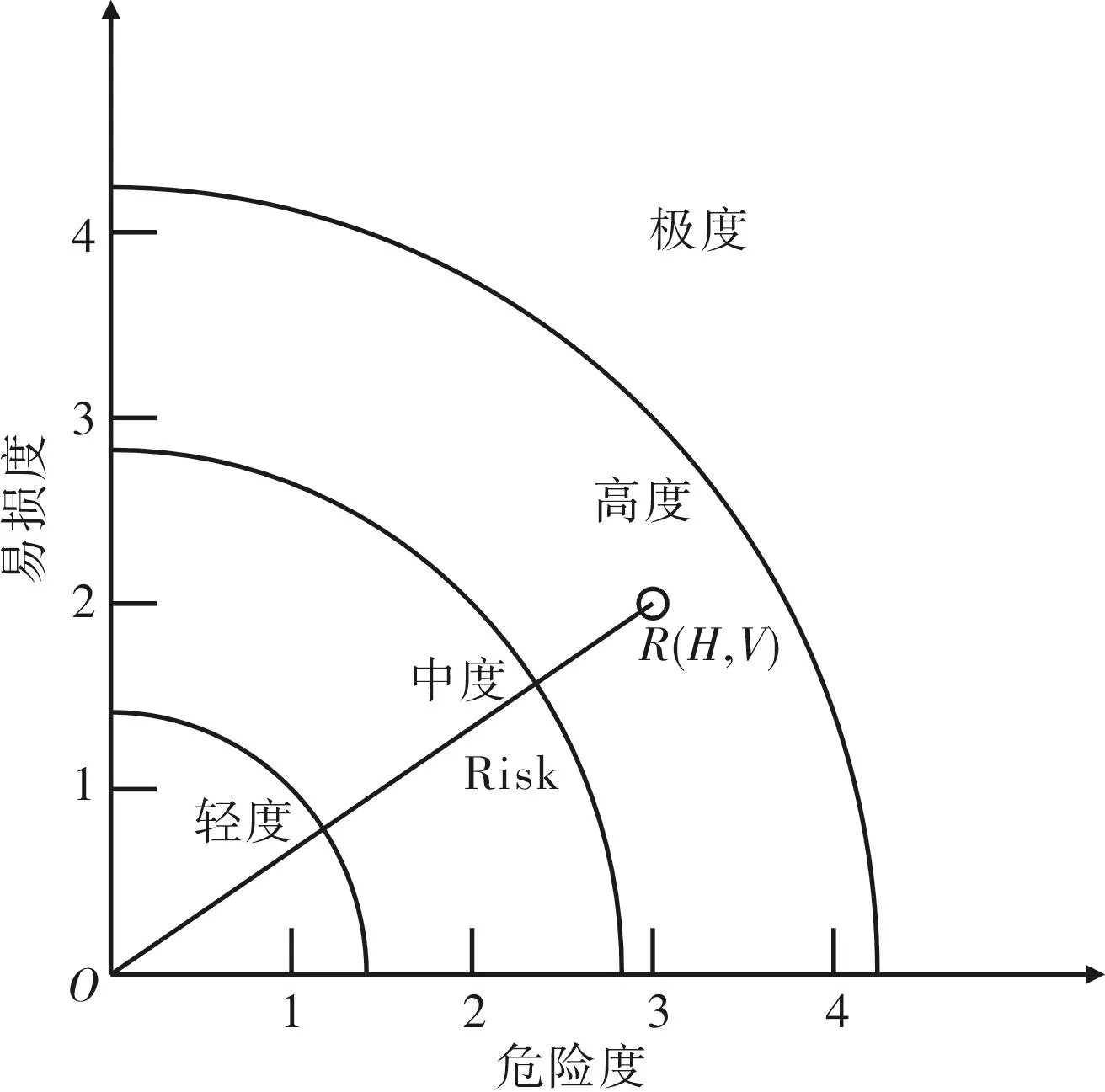
图3　模糊坐标系

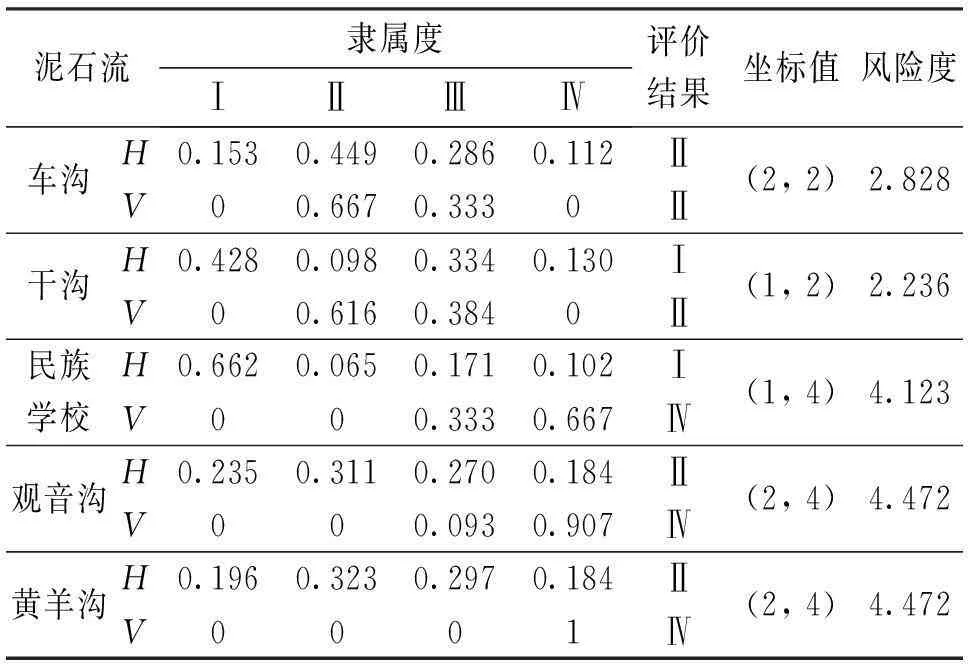
泥石流隶属度ⅠⅡⅢⅣ评价结果坐标值风险度车沟H0.1530.4490.2860.112Ⅱ(2,2)2.828V00.6670.3330Ⅱ干沟H0.4280.0980.3340.130Ⅰ(1,2)2.236V00.6160.3840Ⅱ民族学校H0.6620.0650.1710.102Ⅰ(1,4)4.123V000.3330.667Ⅳ观音沟H0.2350.3110.2700.184Ⅱ(2,4)4.472V000.0930.907Ⅳ黄羊沟H0.1960.3230.2970.184Ⅱ(2,4)4.472V0001Ⅳ

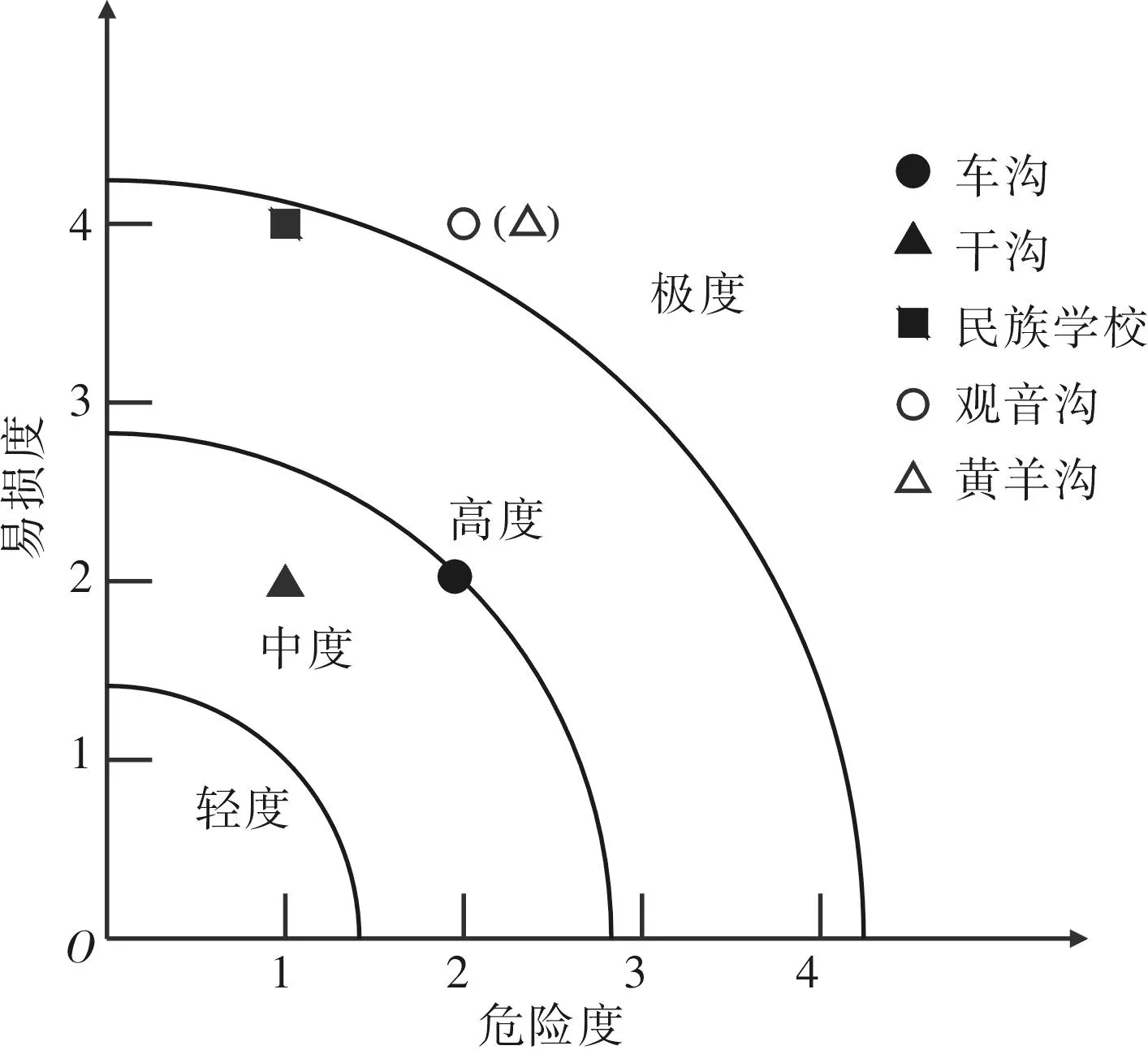
图4　计算结果

分析计算结果可得出如下结论。

(1)车沟泥石流具有中度风险，干沟泥石流具有中度风险，民族学校泥石流具有高度风险，观音沟泥石流具有极度风险，黄羊沟泥石流具有极度风险。

(2)车沟、干沟、民族学校、观音沟、黄羊沟泥石流的危险度等级分别为Ⅱ级、Ⅰ级、Ⅰ级、Ⅱ级、Ⅱ级，神农架林区内的5条泥石流危险度不高；

(3)车沟泥石流的坐标为(2,2)，具有Ⅱ级危险度和Ⅱ级易损度，干沟泥石流的坐标为(1,2)，具有Ⅰ级危险度和Ⅱ级易损度，两条泥石流皆表现为“灾少害小”的特点；

(4)民族学校泥石流的坐标为(1,4)，具有Ⅰ级危险度和Ⅳ级易损度，观音沟及黄羊沟泥石流的坐标都为(2,4)，具有Ⅱ级危险度和Ⅳ级易损度，三条泥石流皆表现为“灾少害大”的特点。

4.3比较分析

将模糊综合评价法与模糊坐标法的计算结果进行比较分析(表4、表5)，得出以下结果。

(1)模糊综合评价法和模糊坐标法的计算结果都能反映泥石流风险的大小，但后者的计算结果还能同时反映泥石流的危险度及易损度大小，表现泥石流风险的具体特点。

(2)模糊综合评价法和模糊坐标法的风险度计算结果略有差异，干沟泥石流用两种方法的计算，风险度分别为高度、中度，民族学校泥石流用两种方法计算，风险度分别为极度、高度。分析调查资料可知，模糊坐标法的评价结果更符合实际，模糊综合评价法的计算结果偏大。

5结论

(1)在既有的泥石流危险度模糊综合评价模型中加入易损度因子，可建立泥石流风险度模糊综合评价模型，该模型可应用于工程实际。

(2)将模糊综合评价法与平面坐标结合，提出一种新的泥石流风险评价法：模糊坐标法。该方法继承了模糊综合评价法对多因素、多层次的复杂问题评价效果好的特点，并利用平面坐标的二维属性使得评价结果能同时表现泥石流的危险度及易损度。该方法既能反映风险的大小，又能表现某个泥石流风险的具体特点，可为防灾减灾的决策提供更详细的信息。

(3)模糊坐标法的风险评价结果更符合实际，模糊综合评价法的风险评价结果会出现偏大的情况，计算结果偏安全。

参考文献：

[1]刘希林, 莫多闻. 泥石流风险及沟谷泥石流风险度评价[J]. 工程地质学报, 2002, 10(3): 266-273.

[2]王学武, 石豫川, 黄润秋, 等. 多级模糊综合评判方法在泥石流评价中的应用[J]. 灾害学, 2004, 19(2): 1-6.

[3]莫时雄, 程峰, 王杰光, 等. 典型金属矿山泥石流潜势度的模糊层次综合评判[J]. 中国地质灾害与防治学报, 2009, 20(2):41-45.

[4]周志广, 李广杰, 陈伟韦. 磐石市富太镇泥石流危险性评价与危险范围预测[J]. 水文地质工程地质, 2007, 34(2):101-105.

[5]罗冠枝, 徐林荣. 基于粗糙集和灰色理论的模糊综合定权法在泥石流危险性评价中的应用[J]. 安全与环境工程, 2008, 15(3):1-5.

[6]陈伟, 任光明, 左三胜. 泥石流危险度的模糊综合评判[J]. 水土保持研究, 2006, 13(2):138-139.

[7]张勇慧, 李红旭, 盛谦, 等. 基于模糊综合评判的公路岩质边坡稳定性分级研究[J]. 岩土力学, 2010, 31(10):3151-3156.

[8]AkgunA,DagS,BulutF.Landslidesusceptibilitymappingforalandslide-pronearea(Findikli,NEofTurkey)bylikelihood-frequencyratioandweightedlinearcombinationmodels[J].EnvironmentalGeology, 2008, 54(6):1127-1143.

[9]王春磊, 吴云刚, 隗锦涛. 模糊综合评判法在泥石流危险度评价中的应用[J]. 安全与环境工程, 2010, 17(3):14-16.

[10]ChangTC.Riskdegreeofdebrisflowapplyingneuralnetworks[J].NatureHazards, 2007, 42: 209-224.

[11]贺拿, 陈宁生, 曾超. 泥石流起动机理研究现状及趋势[J]. 灾害学, 2013, 28(1):121-125.

[12]严炎, 葛永刚, 张建强,等. 四川省汶川县簇头沟“7.10”泥石流灾害成因与特征分析[J]. 灾害学, 2014, 29(3):229-234.

[13]DZ0238-2004地质灾害分类分级(试行)[S]. 北京: 中国标准出版社, 2005.

[14]郭金玉, 张忠彬, 孙庆云. 层次分析法的研究与应用[J]. 中国安全科学学报, 2008, 18(5): 148-153.

Assessment on Debris Flow Risk based on Fuzzy Comprehensive Evaluation Method

Shen Jian, Rao Jun and Fu Xudong

(SchoolofCivilandArchitecturalEngineering,WuhanUniversity,Wuhan430072,China)

Abstract:Vulnerable degree factors are added into the existing fuzzy comprehensive evaluation model of debris flow risk to establish for the first time the comprehensive evaluation model of debris flow risk ambiguity. Based on this model, risk assessment is done to five debris flows in Shennongjia Forest Region, and the results show that fuzzy comprehensive evaluation model could be used in debris flow risk assessment. According to the problem——the calculation results of fuzzy comprehensive evaluation model can reflect the size of the risk, but is unable to reflect the risk characteristics, and combing fuzzy comprehensive evaluation method with the plane coordinate, a new debris flow risk assessment method——fuzzy coordinate method is put forward. Fuzzy comprehensive evaluation on risk and vulnerability of a debris flow are done by the new method, with the evaluation results as coordinate points, define the distance from coordinates to the origin point as the risk degree, the evaluation results can reflect the risk and performance of vulnerability by using the two-dimensional characteristic of plane coordinate and the specific characteristics of the debris flow risk can be expressed.

Key words:fuzzy comprehensive evaluation; debris flow; risk assessment; fuzzy coordinate; evaluation factor

doi:10.3969/j.issn.1000-811X.2016.02.033

中图分类号：TU 473；X 43

文献标志码：A

文章编号：1000-811X(2016)02-0171-05

作者简介：沈简(1991-)，男，湖北武汉人，硕士研究生，主要从事滑坡、泥石流等地质灾害方面的研究. E-mail:slshm@qq.com通讯作者：傅旭东(1966-)，男，湖北孝感人，教授，博士生导师，主要从事边坡及桩基方面的研究. E-mail：xdfu@whu.edu.cn

基金项目：国家科技支撑计划课题(2014BAL05B07)

*收稿日期：2015-08-24修回日期：2015-10-15

沈简，饶军，傅旭东. 基于模糊综合评价法的泥石流风险评价[J].灾害学, 2016,31(2):171-175.[ Shen Jian, Rao Jun and Fu Xudong. Assessment on Debris Flow Risk based on Fuzzy Comprehensive Evaluation Method[J].Journal of Catastrophology, 2016,31(2)：171-175.]