地质灾害保费及其实证研究——以湖南省娄底市为例*

欧阳迪飞，谷　玉，甘　柳，李应求

(1.长沙理工大学 数学与计算科学学院，湖南 长沙 410004;2.湖南商学院 财政金融学院，湖南 长沙 410205)



地质灾害保费及其实证研究
——以湖南省娄底市为例*

欧阳迪飞1，谷玉1，甘柳2，李应求1

(1.长沙理工大学 数学与计算科学学院，湖南 长沙 410004;2.湖南商学院 财政金融学院，湖南 长沙 410205)

摘要:采用随机模拟技术对地质灾害风险损失进行模拟，利用在险价值(VaR)方法计算各个风险区域的保费规模，以此研究地质灾害保险的价格，并用控制变量法研究投保率对保险价格的影响。实证研究以湖南省娄底市2008-2013年地质灾害损失为研究样本，计算出各风险区域的总保费和人均保费，结果表明保费均在可接受的范围内，同时它还能很好地反映风险，风险越高保费越高。投保率是影响保费的重要因素之一，投保率越低保费越高。

关键词:地质灾害；保费；在险价值；VaR方法；随机模拟

由于生态环境恶化，近年来地质灾害发生频率在不断增大，给人们的生命财产造成巨大损失。相关部门越来越重视地质灾害的防治工作，现已形成了具有中国特色的防治体系，并成功临灾避让地质灾害1.5万多起[1]。但是由于地质灾害具有较强的突发性，影响因素众多，许多不确定的因素导致预报很难完成，使得我国地质灾害防治形势依然相对严峻。灾后的救助方面，我国主要依靠政府部门和社会捐助，存在补偿程度较低、政府压力大、资金利用率低等弊端，灾后重建工作主要还是依靠灾民自身。随着保险业的发展，保险补偿慢慢进入人们的视野，成为灾后补偿的一种重要方式，且其具有补偿程度高、资金分配客观等优点。但我国现阶段并未建立地质灾害保险制度，现有的财产保险虽有涉及，但赔付额度较小，地质灾害高发的农村基本都在承保范围之外，因此建立地质灾害保险具有一定的必要性。2015年民盟中央在全国政协会议上建议应尽快推行地质灾害保险制度，随着国家对地质灾害重视程度的进一步提高，建立地质灾害保险制度的进程也将加快，保费作为保险制度的基础，对其进行研究具有较强的实际意义。

地质灾害的研究主要着重于灾害机理、风险评估以灾害的防治等[2-7]，少量关于地质灾害保险的研究侧重地质灾害的可保性[8]、地质灾害保险的可行性[9]和建立保险制度[10]等方面，关于灾后赔偿对策和保费等的相关研究很少。范姣艳[11]等对地质灾害的补偿现状以及存在的问题进行了分析，认为应该根实际情况建立多元化补偿机制；皮曙初[12]提出了建立中国特色灾害损失补偿体系，其为政府主导下的公共部门(P)-市场(M)-公众(P)为一体的宏观保险模式；关于地质灾害保费，欧阳资生[13]认为纯保费是索赔次数期望与赔偿金额期望的乘积，他利用广义帕累托分布和对数分布建立了一个灾害损失模型，在此基础上假设索赔次数服从泊松分布，计算出纯保费。

本文研究的目的是计算出各个风险区域的保费，所采用的方法是VaR方法。首先，在损失分布的基础上采用随机模拟技术，生成地质灾害损失的随机数；然后，利用VaR方法计算出不同置信度下的总保保费，为地质灾害保费的厘定提供参考依据；最后，在已有结论的基础上提出合理的建议供决策部门参考。本文的主要贡献在于将VaR方法引入到地质灾害保费的厘定，此方法与保险定价常用的均衡法和无套利定价法相比，可以很好地处理地质灾害风险的“后尾性”，并且方法简单，操作性强。在计算过程中采用随机模拟技术可以很好的体现地质灾害的突发性与偶然性，提出将风险区域按县级划分，不仅可以让保费很好的反映风险，而且便于保险公司的管理。

1地质灾害保费研究

1.1损失分布拟合

关于地质灾害损失分布的拟合一般从两方面着手：① 以年度损失为单位，对以往每年地质灾害总损失进行拟合，得其分布函数；②以每次损失为单位，对历年每次地质灾害损失分布进行拟合。鉴于我国关于地质灾害损失的数据统计机制建立时间较晚，年度总损失统计的数据较少，若采用第一种方法拟合效果较差，因此本文对历年各次地质灾害损失分布进行拟合。常用的分布函数有对数正态分布、韦伯分布、广义帕累托分布等，现主要介绍本文所用的分布函数[14]，表示如下:

(1)

低于阈值u的数据的分布为F1(x)，常用对数正态分布、指数分布等来刻画。超过阈值u的数据的分布F2(x)采用MGPD:

(2)

式中：x>0,ξ>0,σ>0,θ>0 。

1.2利用VaR方法计算保费

在险价值(VaR)是一种市场风险测量和管理的工具，在险价值法就是为了度量一项给定的资产或负债在一定时间和置信度下其价值最大的损失额。摩根银行在1994年提出的“风险度量制”模型是这种方法的典型代表。VaR的数学表达式为:

P(ΔP>VaR)=α 。

(3)

式中：P表示某事件的概率，ΔP表示在某一定时间内的损失值，α为置信度。

VaR方法[15]可以突显地质灾害损失的厚尾性的特性，计算得到的结果也可以很好的反映风险，相对于其它方法来讲，更适合用于计算地质灾害的保费。计算VaR的方法很多，本文采用蒙特卡洛模拟法，其合理性在于通过计算机模拟地质灾害损失值，既不失一般性，也会得到极值数据，根据不同的置信度计算出不同的在险价值作为保费，为决策者提供一定的参考依据。

在计算保费时，本文假设地质灾害保险无赔付上限与自留额，计算所得保费是最大可能的保费。并假设保险覆盖率为100%，即使如此，若根据全市人口将保费直接平摊有失公允。地质灾害高发区由于自身的风险因素多，应缴纳较多的保费，而低发区则缴纳较少的保费，因此应先划分风险区域，再计算出各个地区的人均保费。

2实证研究

2.1地质灾害损失数据的分布拟合

本节以湖南娄底市国土资源局提供的2008年至2013年地质灾害报表的数据为研究样本，该报表以次为单位记录，并且按照2003年11月19日国务院第29次常务会议通过并于2004年3月1日起施行的《地质灾害防治条例》[16]第四条规定将灾害级别分为三类:大型、中型和小型，除了部分未达到统计标准的不会通报之外，其他的数据都有记录。

地质灾害损失数据一般具有厚尾性，李应求[17]等利用样本经验平均超出函数图(SMEF)以及Q-Q图法进行检验得出娄底市2008-2013年地质灾害损失数据的确具有厚尾性。在对损失分布进行拟合时利用扩展BurrXII分布构建了改进的广义帕累托分布模型——MGDP模型，以分段函数的形式表示，结合平均超出函数法进行多次模拟来确定阈值，关于阈值以下的采用对数正态分布拟合，阈值之上的采用MGPD、韦伯分布、指数分布分别进行拟合，经比较MGPD的拟合效果更好，最终将样本的分布函数如下所示。

(4)

2.2保费价格厘定

保费因地制宜才能很好地反映风险，在计算保费之前，合理地划分风险区域尤为重要。本文研究的对象为湖南省娄底市，若以乡镇为单位进行划分，由于地域单位太小，会使计算更加繁琐，且实用性不强，因此本文以县(区)为单位划分风险区域。现阶段保险公司网点设立也只到县级，以县(区)为单位也便于管理，通过分析历史统计数据知娄底市娄星区地质灾害的风险低，因此本文不予考虑。

保费厘定主要是基于分布函数(式4)进行蒙特卡罗模拟得到损失值，并采用VaR方法计算不同置信度下的保费。为了简单起见，我们假设地质灾害覆盖率为100%，地质灾害保险无赔付上限与自留额，地质灾害保险风险由保险公司独立承担。对保险公司来说，地质灾害发生的次数越多、经济损失越大，以及伤亡人数越多的地区，风险权重就越大，我们定义娄底市某个县的风险权重为该县地质灾害频次、经济损失值、伤亡人数三者之和除以娄底市的三者之和，在计算之前先对数据进行无量纲化处理，利用历年数据计算出相应的风险权重值，从娄底市人民政府官网查到全国第六次人口普查娄底市各个县人口数如表1所示。采用蒙特卡罗模拟得出10 000组损失值，其统计特征如表2所示。

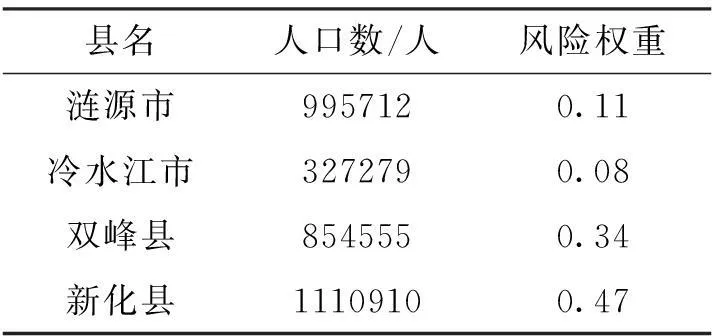
表1　娄底市各县人口与风险权重

表2　模拟数据相关统计量

由表2可知，模拟数据的均值为33.964，与原数据的均值33.740 3相差不大，因此模拟具有合理性与可行性，利用这10 000组数据计算不同置信度下的娄底市的总保费规模，所得结果如表3所示。

表3　不同置信度下的保费规模

由表3可以看出，不同的置信度下保费相差较大，这是因为地质灾害损失具有尖峰厚尾性，巨型地质灾害发生的概率极小，所以置信度越高保费越高，并且在置信度越高的情况下，置信度的波动带来保费变化比置信度较低的情况下较大，例如99%的置信度下的保费为204.9万元，99.5%的置信度下保费为269.2万元，即置信度变化0.5%而保费相差了65万元，但置信度较低时，置信度从85%变化到90%，置信度变化5%，保费只相差17.4万元。

对保险公司而言，置信度的实际意义则表示有多大的概率保证公司不破产，不破产概率越大保费自然越高，例如，如果某家保险公司开发娄底市地质灾害保险业务，只有收取不少于107.1万元的保费才有95%的可能性导致公司不因地质灾害的保险赔偿而破产，但若降低破产概率，使其不破产概率增加到99.5%，则收取的保费要达到269.2万元，这与实际规律也是相符的。表3可以为保险公司制定地质灾害保险收取保费提供参考依据。

表3中的保费是发生一次地质灾害的总保费，并未得到娄底市各风险区的年人均保费，为此，还需将保费依据风险权重分摊到各地区，再依据人口数计算平均保费。结合表1给出了娄底市各地区的风险权重与人口数，可以得到各地区一次灾害总保费如表4所示，人均次保费如表5所示。

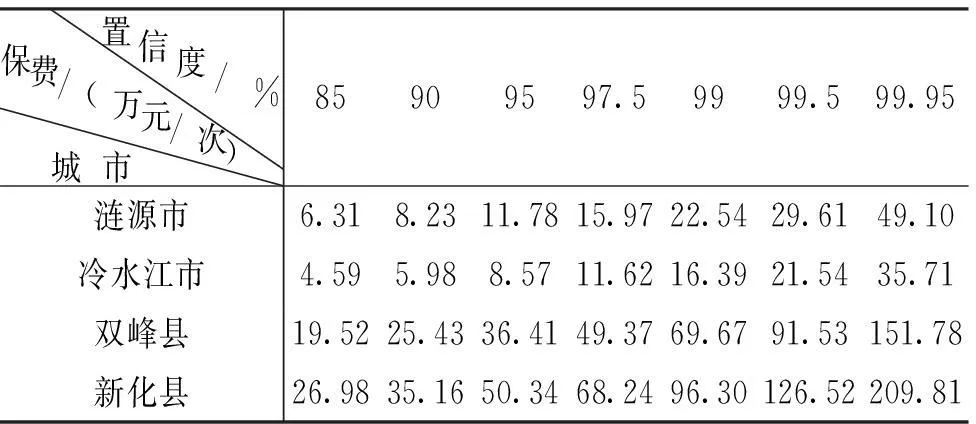
表4　娄底市各个县(区)在不同置信度下的总保费

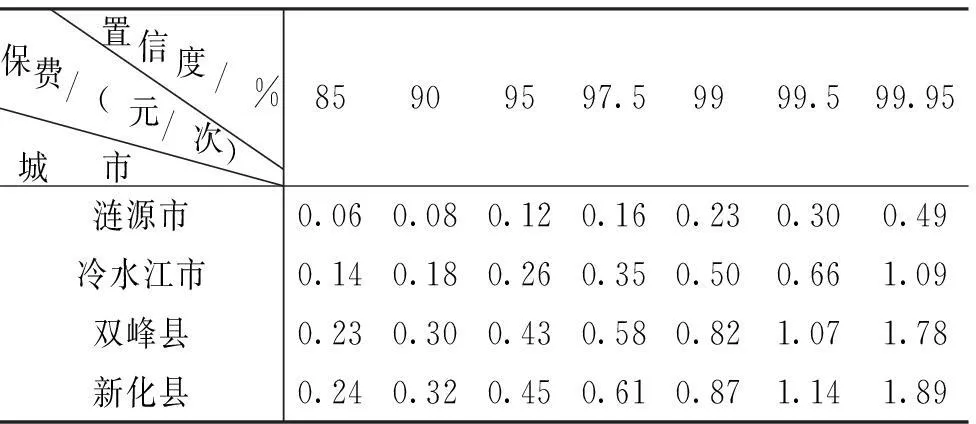
表5　娄底市各个县(区)在不同置信度下的人均次保费

保费如果按照灾害发生的次数收取，对保险公司来说将不便于管理，一般以年为单位收取，而地质灾害的发生具有季节性，主要集中于第二、三季度，因此收取年保费较为合理。将表5计算出的每次地质灾害的人均保费乘以各县年平均发生地质灾害的次数，得出不同的置信度下各地区人均年保费如表6所示。

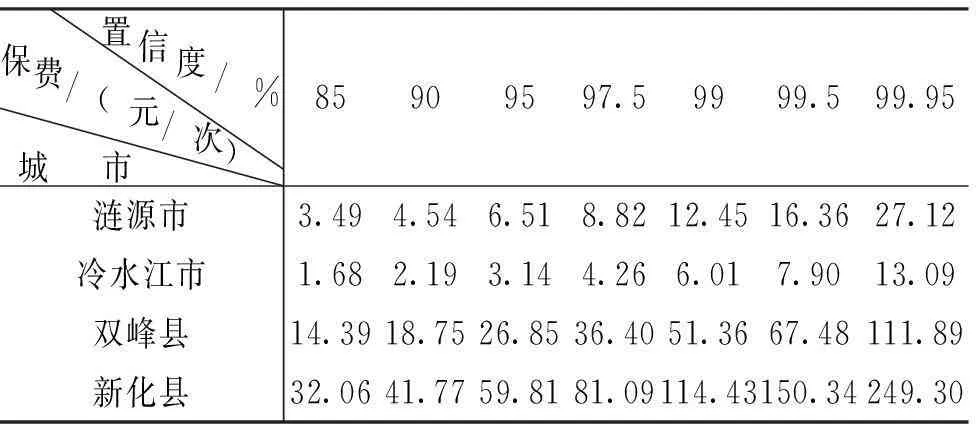
表6　娄底市各县(区)在不同置信度下的人均年保费

从表6中可以看出,置信度越高，保费越高；地质灾害高发和损失严重的地区保费也越高，即使置信度高达99.95%，人均年保费也都在可接受的范围内.

表6所示保费是在投保率为100%的假设下计算得出的，但在现实生活中投保率很难到达100%，为了便于分析投保率对保费的影响，本文以表6中新化县不同置信度下的人均保费为基础，计算出不同的投保率下的人均保费如表7所示。

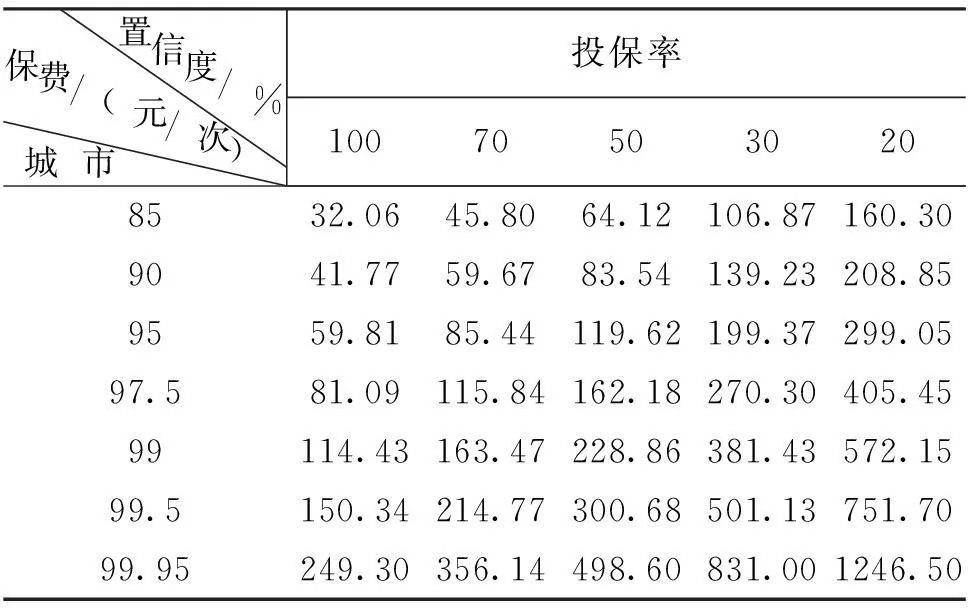
表7　新化县在不同的投保率下的人均保费

由表7可以看出:投保率对保费的影响结果非常明显，投保率越低，人均保费越高，不同的投保率之间人均保费相差甚远，当投保率为20%时，人均年保费高达上千元，这对于地质灾害高发区的山区农民来讲，远远超出其承受范围，同样对保险公司来说其破产概率也会增大。

3结论与建议

关于在我国，特别是在湖南省建立地质灾害保险制度的问题，通过上面的理论和实证研究，我们得到如下结论。

(1)保费均在可接受的范围之内。根据风险计算的保费只有具有一定的合理性才具有实用性，从表6中可以看出，即使置信度达到99.95%，最高的保费每年只需要249.3元，在可承受的范围之内，可以作为相关部门制定保费的参考依据。

(2)保费应该很好地反映风险。由于地域因素的影响，同一置信度下娄底市不同的地区总保费相差很大，从表4可以看出，在置信度为85%时，处于地质灾害低发区的冷水江市发生一次地质灾害的保费为4.59万元，而高发区的新化县为26.98万元，由此可知风险与保险价格是相对应的，风险越高，保费越高，而对保险公司来讲，只有收取更多的保费才会增大其不破产概率，这也是与实际情况相符的。

(3)置信度是保费的重要影响因素。由表6可以看出各地区不同置信度下的人均保费都存在差异，即使置信度发生较小的变化，保费也会产生较大的改变。不同置信度下的保费则可以作为制定不同价格的参考依据，使保费更具有灵活性。

(4)投保率对保费的影响很大。风险权重差异较小时，其发生一次地质灾害的总保费大小相当，同样是在85%的置信度下，涟源市的保费为6.31万元，比冷水江市高1.72万元，但由于涟源市的人口明显比冷水江市多，其人均次保费比冷水江市低，因此保费的投保率也是影响保费的一个重要因素，投保率越高，投保的人数越多，人均保费自然越低，表7则更加具体的说明了这一结论。

根据以上结论，我们做以下建议。

(1)加快地质灾害保险制度的建立。现阶段地质灾害造成的损失严重，对于救助工作，政府部门与社会救助团体心有余而力不足，并且现阶段的救灾工作具有一定的滞后性，地质灾害给人们的生活造成影响，建立地质灾害保险制度，不仅可以加快救灾步伐，改善补偿程度低的现状，而且可以减少政府的压力。

(2)合理划分地质灾害风险区域，不同地区的保费价格应不同。从结论可以看出，地域不同地质灾害的风险权重存在差异，各个地区民众的投保积极性也会存在差异，风险越高的地区民众投保的积极性则会越高，但是保险公司的积极性会相对较弱，而对于地质灾害风险较低的地区情况则会相反，因此按地区收取不同的保费不仅可以调动民众投保的积极性，而且保费还能很好的反映风险。

(3)建立地质灾害保险制度应扩大保险覆盖率。在全民参与的假设下计算的保费，均在可承受的范围之内，但表7的比较分析可知投保率对保险的价格影响较大，投保率越低，保费越大，将会超出民众的承受范围，投保积极性减弱，影响保险市场的稳定。保险的需求越大价格越低廉，因此可通过加大对地质灾害保险的宣传、政府给予适当的补贴等措施使更多的民众投保。

(4)地质灾害保险制度里政府应占主导地位。地质灾害高发区大多处于较为偏僻的山区，受传统文化和环境的影响，民众对保险的认识不足，有一定的抵触心理，投保积极性较弱，但是其对政府的信赖度较高，只要政府出面，他们则会积极响应国家的制度政策。由于偏远地区民众的收入水平较低，如果保险的覆盖率较低时，地质灾害的保费对一个家庭来说还是一笔不小的开支，因此政府可以制定相应的政策，将地质灾害保险指定为强制保险，这样可以扩大保险的投保率，降低保费，同时政府还可以建立相应的基金项目，对地质灾害保费进行补助，也可以减轻民众的经济负担。

参考文献:

[1]李乾坤,石胜伟,韩新强,等.国内地质灾害机理与防治技术研究现状[J].探矿工程,2013,40(7):52-54.

[2]卢全中,彭建兵,赵法锁.地质灾害风险评估(价)研究综述[J].灾害学,2003,18(4):59-63.

[3]徐继维,张茂省,范文.地质灾害风险评估综述[J].灾害学,2015,30(4):130-134.

[4]刘传正.论地质灾害防治的科学理念[J].水文地质工程地质,2013,40(6):1-7.

[5]徐卫亚,孙广忠.论地质灾害防治对策及其系统决策[J].灾害学，1992,7(3):19-24.

[6]韦仕川,杨杨,栾乔林,等.美国地质灾害防治的经验总结及启示—灾害防治的“规划软措施”[J].灾害学,2014,29(3):156-161.

[7]张小趁,陈红旗.突发地质灾害应急技术：过程模式[J].灾害学,2015,30(4):149-155.

[8]毛学翠.论地质灾害风险与保险[J].中国国土资源经济,2006,4:31-33.

[9]王艳萍.设立地质灾害保险独立险种的可行性研究[J].西部资源,2006,3(12)：9-10.

[10]姜建军.我国地质灾害保险制度探讨[J].国土资源科技管理,2008,25(6):91-93.

[11]范姣艳,张凡.三峡库区地质灾害防治工作及补偿制度评析[J].前言,2009(12):64-67.

[12]皮曙初.重构中国特色灾害损失补偿体系探讨[J].保险研究,2013(9):105-111.

[13]欧阳资生.地质灾害损失分布拟合与风险度量[J].统计研究,2011,28(11): 78-83.

[14]Shao Quanxi,Wong Heng, Xia Jun, et al.Models for extremes using the extended three parameter Burr XII system with application to flood frequency analysis[J].Hydrological Sciences-Journal-des Sciences Hydrologiques,2004,49(4):685-702.

[15]田玲，姚鹏.地震保险费率厘定研究[J].北京理工大学学报,2013,3(15):54-59.

[16]地质灾害防治条例[EB/OL].(2004-06-25)[2015-05-24]. http://www.mlr.gov.cn/zwgk/flfg/dzhjgl/200406/t20040625_13574.htm.

[17]欧阳迪飞,杨扬,李应求,等.基于MCMC模拟的MGPD模型及其在地质灾害风险度量中的应用[J].经济数学,2015(2)：101-106.

Geological Hazard Premium and its Empirical Study—A Case Study of Loudi City in Hunan Province

Ouyang Difei1, Gu Yu1, Gan Liu1and Li Yingqiu1

(1.SchoolofMathematicsandComputingScience,ChangshaUniversityofScienceandTechnology,Changsha410004,China; 2.SchoolofTreasuryandFinance,HunanUniversityofCommerce,Changsha410205,China)

Abstract:Risk losses of geological disasters are simulated by stochastic simulation technique. Using the Value at risk (VaR) method to calculate premium scale in each risk area, and in order to study geological disaster insurance prices, we use the control variable method to research the insured rate influence on the price of insurance. The empirical study takes the geological disaster loss of as the research sample in Loudi City during 2008-2013. By calculating the total premium and the premium per capita in the risk area and the results show that the premium is acceptable. At the same time, it can reflect the risk and the higher the risk, the higher the premium. Insurance rate is one of the important factors that affect the premium. The premium rate increase with the rate.

Key words:geological hazard; premium; value at risk; VaR method; stochastic simulation

doi:10.3969/j.issn.1000-811X.2016.02.021

中图分类号：X43； F842.6

文献标志码：A

文章编号：1000-811X(2016)02-0106-05

作者简介：欧阳迪飞(1965-)，女，湖南望城人，副教授， 主要从事概率统计研究.E-mail:ouyangdifei1965@sina.com 通讯作者：谷玉(1991-)，女，湖南常德人，硕士研究生，主要从事应用统计研究.E-mail:guyu199105@163.com

基金项目：国家自然科学基金项目(11571052，11171044)；湖南省国土资源科技项目(2013-28)；长沙理工大学研究生科研创新项目(CX2015SS19)

*收稿日期：2015-10-10修回日期：2015-12-04

欧阳迪飞，谷玉，甘柳，等. 地质灾害保费及其实证研究——以湖南省娄底市为例[J].灾害学, 2016,31(2):106-110.[ Ouyang Difei， Gu Yu，Gan Liu,et al. Geological Hazard Premium and its Empirical Study—A Case Study of Loudi City in Hunan Province[J].Journal of Catastrophology, 2016,31(2)：106-110.]