蒙特卡罗模拟CFETR中子输运计算中的全局减方差方法应用及对比

聂星辰　李 佳　赵平辉　祝庆军（中国科学技术大学 核科学技术学院　合肥 3007）（中国科学院等离子体物理研究所　合肥 3003）



蒙特卡罗模拟CFETR中子输运计算中的全局减方差方法应用及对比

聂星辰1李 佳1赵平辉1祝庆军2
1（中国科学技术大学 核科学技术学院合肥 230027）
2（中国科学院等离子体物理研究所合肥 230031）

摘要在具有全局特性的蒙特卡罗输运精细计算的问题中，传统的MCNP(Monte Carlo N Particle Transport Code)局部减方差方法很难得到理想的计算结果，全局减方差方法(Global Variance Reduction,GVR)则是一种有效的解决方法。针对中国聚变工程试验反应堆(Chinese Fusion Engineering Testing Reactor,CFETR)的中子输运过程中减小全局方差的问题，将多种形式的GVR方法应用到柱状CFETR中子学模型的计算中。依据不同的中子分布信息，在算例中应用和对比了6种不同形式的GVR权窗，并对不同GVR方法的品质因子(FOMG)、标准差(σ)和有效计数率(Scoring)进行了分析。与AN(MCNP analog method)相比，GVR方法的FOMG有很大的增长，误差在空间的分布也更加平缓，且具有更高的Scoring。在前人提出的全局减方差的基础上，在计算中应用一些新的GVR形式（能量、径迹数等），计算结果表明，基于中子通量的GVR方法的全局计算效率较AN提高了6.43倍。此外，基于中子能量的全局减方差方法也是一种可行的GVR应用形式，其与AN比较，计算效率提高了5.11倍。综上，基于中子通量的GVR方法具有最佳的全局减方差效果。

关键词全局减方差，权窗，蒙特卡罗，MCNP，中子学

磁约束核聚变国家特殊项目(No.2013GB108004、No.2015GB108002)、国家自然科学基金(No.11175207)资助

第一作者：聂星辰，男，1990年出生，2013年毕业于南华大学，现为硕士研究生，核能科学与工程专业

Supported by National Special Project for Magnetic Confined Nuclear Fusion Energy(No.2013GB108004,No.2015GB108002)and the National Natural Science Foundation of China(No.11175207)

Frist author:NIE Xingchen,male,born in 1990,graduated from University of South China,master student,major in nuclear science and engineering

Application and comparison of global variance reduction methods employed
in Monte Carlo neutron transport for CFETR

NIE Xingchen1LI Jia1ZHAO Pinghui1ZHU Qingjun2
1(School of Nuclear Science and Technology,University of Science and Technology of China,Hefei 230027,China)2(Institute of Plasma Physics,Chinese Academy of Sciences,Hefei 230031,China)

AbstractBackground:For the detailed Monte Carlo radiation transport,which possesses global characteristics,traditional MCNP Localized Variance Reduction(LVR)methods can hardly perform well.Global Variance Reduction(GVR)method is an effective way.Purpose:This study aims to decrease the global variance of Monte Carlo radiation transport calculations for Chinese Fusion Engineering Testing Reactor(CFETR).Methods:According to different information of neutron distribution,six kinds of GVR methods were implied and compared in a cylinder CFETR neutronics model.Global figure of merit(FOMG),standard deviation(σ)and the percentage of scoring were analyzed.Based on predecessors’ research,other kinds of new GVR methods(energy,tracks)were applied in this calculation.Results:In the point of GVR methods,FOMGincreased dramatically,spatial variation inrelative errors was more gradual,and the scoring was higher,compared with AN.The GVR method based on neutron flux achieved the global calculation efficiency of 6.43 times that of AN.Apart from that,the GVR method based on neutron energy can also be a practical GVR kind,achieving the global calculation efficiency of 5.11 times that of AN.Conclusion:The GVR method based on neutron flux can performed best that has a well function of global variance reduction,achieving the global calculation efficiency.

Key wordsGlobal variance reduction,Weight window,Monte Carlo,MCNP,Neutronics

针对中国聚变工程试验反应堆(Chinese Fusion Engineering Testing Reactor，CFETR)在整个空间中的高分辨中子输运计算和停堆剂量率分析的需求越来越大。在该工程的中子学分析中，由于CFETR具有庞大的体积和大量的屏蔽材料，而由此引发的中子深穿透问题会致使蒙特卡罗模拟(Monte Carlo,MC)很难给出理想结果。就此类具有全局特性的中子输运问题[1-6]，需要给出中子通量的时间－空间－能量的精细分布。故而提出了如何获取可靠全局解的问题。

MC模拟结果的精度与样本数、方差有关。通过增大样本数或减小方差都可以提高计算精度。依靠大规模并行机的优势，可以增加样本数，但由于模型的特殊性所带来的中子深穿透问题，故仅依靠增大样本数不能从根本上解决中子通量在全局的精细分布计算问题[7]。而提高精度的另一条途径是减方差。

通过在MC中使用减方差技巧，可以有效提升中子对于计数器的贡献率，提高模拟的计算效率。一种常用和有效的减方差方法是使用权窗[4-6]。权窗的作用是依据重要性调整中子的权重，通过设定权窗的参数可以有效控制区域内的中子权重，进而可以避免由输运过程中的权震荡而造成的统计结果误差过大的情况。对于具有全局特性的MC输运计算问题，传统的MCNP局部减方差方法(Localized Variance Reduction,LVR)[5-6]中的权窗技巧由于针对的是特定的计数器或目标空间区域，因而LVR很难得到理想的全局计算结果。

为解决具有全局特性的MC输运计算问题，本文介绍了全局减方差方法(Global Variance Reduction,GVR)[1-4]。GVR主要功能是将中子输运到模型的全局空间中，使得MC结果的相对误差在全空间中的每处都相对理想，可以有效减少模型全局的计算方差。本文依据MC的中子分布初始信息来获取GVR权窗和重要性，并对比和分析了不同形式的GVR权窗在CFETR全局特性的MC输运计算中的效率。

1　全局减方差原理

相比于传统的LVR方法，GVR方法在整个模型空间中都可以获得较可信的中子通量精细分布，具有很好的全局减方差效果。当感兴趣区域是全局空间或目标计数器分布在全空间中时，采用GVR方法会使得测量结果的相对误差随空间分布的梯度尽可能小，进而提高整个空间模型中的平均探测效率。为获取全局空间里中子通量的分布，通过迭代的手法，以提高系统内的重要性分布的清晰度，以此指导MC中子输运的径迹走向，最终达到全局降方差的目的。

这里需要指出的是为获取全空间里可信的中子通量分布，可以针对全空间的目标计数器，使用MCNP权窗生成器来自动产生针对全空间的权窗。但是对于一个占有较大空间的复合靶栅元，直接使用权窗生成器具有一定的风险性。根据权窗重要性理论，该方法的直接后果是生成的权窗只会对中子较为容易输运到的空间起效果，而对其他区域抽样不均匀。相比之下GVR方法是使用初始的MC模拟的相关中子信息来设定权窗的下阈值，进而通过MCNP 内置的WWP(Weight window parameter)卡构建出GVR权窗。Wth为权窗下边界，Wsplit为权窗上边界，定义两者比值β，如式(1)所示，其在MCNP5中默认值是5。

对于基于中子通量φ的GVR方法，在低中子通量和高计算误差的区域，权窗具有较低的下边界，使得该区域有更多的中子发生分裂，增加中子数的样本以降低误差，提高计算精度。而在高通量和低误差区域，权窗具有相对高的下边界，使得在该区域有更多的中子参与了俄罗斯轮盘赌，降低样本以减少计算时间，而增加计算效率。所以在GVR权窗的作用下，中子的密度即会在低通量和高误差区域相对升高。特别的，对于固定中子源的计算模型，其源所在的区域往往是最高中子通量Max(φ)所在的区域，如本算例中Max(φ)在等离子体区内。在栅元i处基于中子通量φi的下边界定义如下[2]：

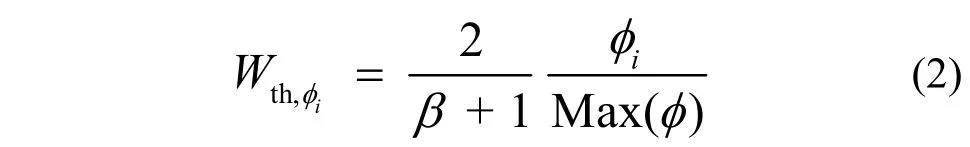
对于基于GVR方法的权窗或重要性值，其中子分布信息可以从标准MCNP输出文中所得。使用该分布信息（可以用中子通量、中子数量、权重等形式）来产生基于栅元或网格的GVR权窗，也可以依据重要性值和权窗阈值之间的反比关系，由式(2)反推出重要性分布，如式(3)。将GVR方法应用到IMP(Importance)卡中，通过IMP的几何分裂和俄罗斯轮盘赌原理来实现全局减方差目的也是种可行的途径。

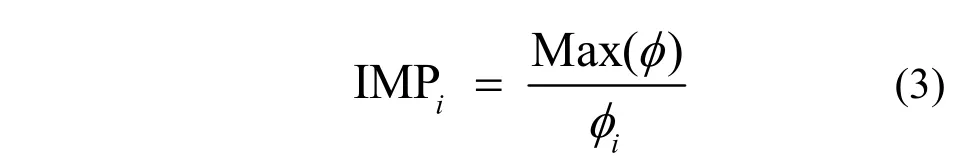
由最初的AN方法来获取的中子分布信息在中子高衰减区域可能会缺失，但它为以后提供了迭代依据。每次迭代都会改善中子信息的空间分布情况。在GVR方法中使用多群和能量截断的方法可以有效提高迭代速率[1]。基于中子通量的GVR方法的实践步骤如图1。通过判断在目标区域内是否有足够抽样作为停止迭代的依据。初始能量截断的值较高(10-3MeV)，以便缩短初始迭代的计算时间，而使整体的迭代过程有较快起步。在迭代的进程中逐步降低能量截断的值，可以提高每个中子历史的平均寿命，而获得空间中更加精细的中子分布。

图1　基于中子通量的GVR方法的骤流程图Fig.1　Flow chart of GVR method based on neutron flux.

需注意在低通量区域，毗连区域的通量衰减很快，当直接采用式(2)算得到的权窗具有很高的梯度变化，这种非常危险的减方差行为会使得中子的权重变化巨大，出现中子过度分裂的现象，而大大增加了一个中子历史的计算时间。特别在并行计算的情况下，该现象会严重恶化计算效率。为缓解这种由于过度偏倚现象所带来的中子输运的长历史问题，本文通过设定通量的误差阈值，而对通量的结果进行筛选，当通量的相对误差Re超过限值时将关闭权窗或者统一地设定权窗值，而没有使用全部的通量结果进行计算。通过数值实验表明这种方法可以防止权窗在空间中有较大的振荡，有效缓解了长历史问题。

2　全局减方差评估参数

MCNP中的 FOM公式作用是衡量给定的计数器的计算效率，而对于GVR方法的计算效率则是反应在整个空间分布中的计数器的效率。由于和传统的LVR作用机制和使用目的不同，这里采用GVR的品质因子FOMG[1]。对于计算效率较好的GVR方法，其具有较少的计算时间和较小的误差统计，从而具有较高的FOMG值。TCPU代表模拟的CPU计算时间，N为栅元或网格的总个数，Rei代表第i个栅元的中子通量的相对误差。FOMG的定义如下：

基于相对误差的标准差σ[2]可以有效衡量通量的相对误差在空间位置上的变化情况。对于GVR方法的计算中，在全局空间上的模拟过程应尽可能表现出较小的误差分布梯度，使得随着中子数历史的增加，整个空间每处的方差以相同的速率收敛。理想GVR方法的σ应尽可能趋近0。其定义如下：

对于零中子通量的栅元，由于MCNP在该区域内没有统计结果，所以该栅元处的通量误差是零，该零通量栅元就不适用于FOMG和σ的计算公式。对于在计算过程中出现的大量零通量栅元，其会影响GVR计算效率的评估。对于零通量栅元，可将相对误差由0修改为1，使得相对误差在空间中尽可能连续，而后可代入FOMG和σ的计算公式。

MCNP的有效计数率(Scoring)可以有效反映出没有计数的零通量栅元的份额，故Scoring也是衡量GVR计算的一个重要指标。综上所述，当FOMG、σ和Scoring的参数都可以接受时，则该GVR方法的全局减方差效果较好。

3　GVR方法的应用和比较

本文将多种GVR形式应用到CFETR水冷陶瓷增殖堆柱状中子学模型的计算中，对各种GVR方法的机理和性能进行比较研究，并对不同GVR方法的FOMG、σ和Scoring进行了分析。模型的几何视图如图2所示，其主要参数见表1。

图2　柱状CFETR中子学模型Fig.2　Cylinder CFETR neutronics model.

表2是基于中子通量的GVR方法的迭代过程。第一次计算的能量截断设置为ECUT=10-3MeV，而后随迭代的次数递减，递减到初始的能量截断值为止(10-9MeV)。随着GVR方法迭代次数的上升，平均误差、σ总体下降，Scoring和FOMG总体上升。数据表明每次的迭代都改善了中子的空间分布情况，增大了MCNP有效计数率，误差在空间的分布更加均匀，提高了全局的平均计算精度，而增加了全局减方差的计算效率。表2中出现了小部分数据没有按趋势变化的情况，造成数据离散的原因可能是因为计算时间过短(0.5 min)，模拟的中子数太少，而造成数据的振荡。

表1　中子学模型主要参数Table 1　Main parameters for neutronics model.

表2　基于中子通量的GVR方法的迭代过程(CPU Time=0.5 min)Table 2　Iterations of GVR method based on neutron flux(CPU Time=0.5 min).

根据中子的相关信息分布可以在一定程度上反应出系统内的重要性分布，参考式(2)的表达形式，利用不同的中子信息去替换通量可以获得其他形式的GVR的权窗。本文应用了6种形式的GVR权窗，并在Davis的基础上[1]，也尝试使用了其他的GVR形式（能量和中子径迹）。由于中子的能量在输运的过程是一个非常重要的参数，且在中子深穿透的过程中其能量也相应降低，利用该规律也可以将中子的能量作为系统内的重要性分布的信息来源，MC中子的径迹也遵循类似的原理。

表3比较了不同GVR方法的主要参数。由于计算模型相对规整，表3中的数据均是一次迭代的结果，使用相同的截断条件。对于没有采取任何GVR方法的模拟(AN)，正如所预期，AN具有最大的平均误差、σ和Scoring和最小的FOMG值。而采用多种GVR方法后，相比与AN，FOMG都有很大的增长，相对误差在空间的分布也更加平缓，且具有更高的计数率。通过对比多种形式的GVR方法可得，基于中子通量的全局减方差方法(GVR-F)具有最好的全局减方差效果。GVR-F与AN比较，其计算效率提高了6.43倍，平均误差降低了1.79倍，σ减少了1.69倍且全局空间都有计数率。基于中子权重的全局减方差方法(GVR-W)也具有很好的全局减方差效率，GVR-W与AN比较，其计算效率提高了5.98倍，平均误差降低了1.77倍。除此以外，本文所提出的基于中子能量的全局减方差方法(GVR-E)也是种可选的GVR应用形式，其与AN比较，计算效率提高了5.11倍。GVR-E较Davis[1]所提出的基于中子数目的全局减方差方法(GVR-P)和 van Wijk[2]的基于中子误差的全局减方差方法(GVR-R)，其全局减方差效率都所提高。

表3　不同GVR方法的主要参数(CPU Time=0.5 min)Table 3　Main parameters of different GVR methods(CPU Time=0.5 min).

图3展示了AN和GVR-F两种方法在CFETR外包层和内包层的中子通量，计算误差和径迹数的分布情况。对于内外包层的中子通量分布，AN的中子通量只在模型部分区域内有探测，其MCNP的有效计数率较低。在较厚区域，AN通量的相对误差值陡增，且迅速到达最大误差值。在使用GVR方法后，通量在整个模型内都有探测结果，且误差在空间中的绝大部分基本保持一个较低的值，变化梯度也较小，减少了全局的方差，进而提高了全局的计算效率。相比于GVR方法，AN的中子径迹衰减很快，在模型的后半段近乎没有中子径迹数，该处的计数器的工作效率极低。而对于采用了GVR方法的中子径迹分布，其在整个模型空间中都有较为可观的径迹分布，从而使得计数器具有较多的信息样本，其探测结果也更可信。

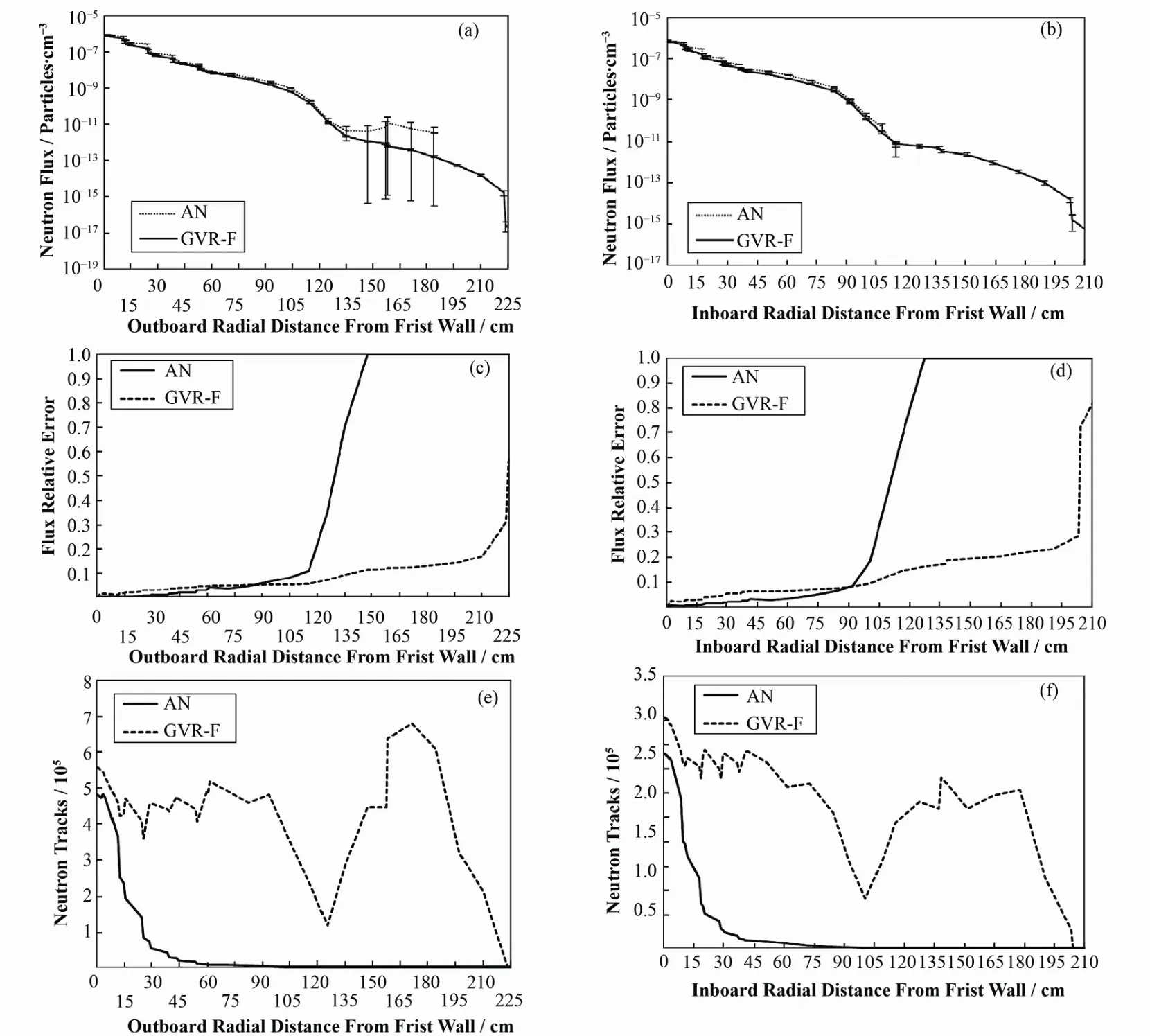
图3　CFETR包层的中子信息分布Fig.3　Neutron distribution information of CFETR blanket.

4　结语

在解决具有全局特性的MC输运的精细计算问题中，本文介绍了多种GVR方法及其应用。通过GVR权窗在CFETR的应用并与AN比较可得，GVR方法的FOMG有很大的增长，通量的平均相对误差较小，且具有更高的计数率。对于不同的GVR方法比较可得，基于中子通量的全局减方差权窗(GVR-F)具有最好的全局减方差效果。GVR-F与AN比较，其计算效率提高了6.43倍。本文所提出的基于中子能量的全局减方差方法(GVR-E)也是种可行的GVR应用形式，其与AN比较，计算效率提高了5.11倍。

除了本文中已使用的GVR形式以外，还可以考虑使用其他的中子分布信息。此外，将GVR方法所获得的重要性分布应用到IMP卡中来实现全局减方差的目的也有种可行的途径。今后也有待将多种GVR方法应用到更加复杂的三维CFETR模型中进行对比和分析。

参考文献

1Davis A,Andrew T.Comparison of global variance reduction techniques for Monte Carlo radiation transport simulations of ITER[J].Fusion Engineering and Design,2011,86:2698-2700.DOI:10.1016/j.fusengdes.2011.01.059

2van Wijk A J,van den Eynde G,Hoogenboom J E.An easy to implement global variance reduction procedure for MCNP[J].Annals of Nuclear Energy,2011,38:2496-2503.DOI:10.1016/j.anucene.2011.07.037

3Naish J,Fox F,Ghani Z,et al.Radiation mapping at JET and ITER using advanced computational acceleration techniques and tools[J].Nuclear Technology,2015,192:299-307.DOI:10.13182/nt14-132

4Cooper M A,Larsen E W.Automated weight windows for global Monte Carlo particle transport calculations[J].Nuclear Science and Engineering,2001,137:1-13.DOI:10.13182/nse00-34

5Booth,Thomas E.MCNP variance reduction examples[R].LA-UR-12 25907(2012),Los Alamos National Laboratory,2004.DOI:10.2172/1054246

6李长楷,汤晓斌,岳爱忠.深贯穿问题脉冲高度计数减方差技巧[J].核技术,2015,38(3):030501.DOI:10.11889/j.0253-3219.2015.hjs.38.030501 LI Changkai,TANG Xiaobin,YUE Aizhong.Pulse-height tally variance reduction in deep penetration problem[J].Nuclear Techniques,2015,38(3):030501.DOI:10.11889/j.0253-3219.2015.hjs.38.030501

7许海燕,黄正丰,蔡少辉.蒙特卡罗中子输运问题的全局降方差方法[J].计算物理,2010,27(5):722-732.DOI:10.3969/j.issn.1001-246X.2010.05.014 XU Haiyan,HUANG Zhengfeng,CAI Shaohui.Global variance reduction method for Monte Carlo particle transport problems[J].Journal of Computational Physics,2010,27(5):722-732.DOI:10.3969/j.issn.1001-246X.2010.05.014

收稿日期：2015-10-22，修回日期：2015-12-24

Corresponding author:LI Jia,E-mail:lijia@ustc.edu.cn

通信作者：李佳，E-mail:lijia@ustc.edu.cn

DOI:10.11889/j.0253-3219.2016.hjs.39.030501

中图分类号TL62