FREE BOUNDARY VALUE PROBLEM FOR THE CYLINDRICALLY SYMMETRIC COMPRESSIBLE NAVIER-STOKES EQUATIONS WITH DENSITY-DEPENDENT VISCOSITY∗

Ruxu LIAN(连汝续)College of Mathematics and Information Science,North China University of Water Resources and Electric Power,Zhengzhou 450011,ChinaInstitute of Atmospheric Physics,Chinese Academy of Sciences,Beijing 100029,ChinaE-mail:ruxu.lian.math@gmail.comJian LIU(刘健)College of Teacher Education,Quzhou University,Quzhou 324000,ChinaE-mail:liujian.maths@gmail.com



FREE BOUNDARY VALUE PROBLEM FOR THE CYLINDRICALLY SYMMETRIC COMPRESSIBLE NAVIER-STOKES EQUATIONS WITH DENSITY-DEPENDENT VISCOSITY∗

Ruxu LIAN(连汝续)
College of Mathematics and Information Science,North China University of Water Resources and Electric Power,Zhengzhou 450011,China
Institute of Atmospheric Physics,Chinese Academy of Sciences,Beijing 100029,China
E-mail:ruxu.lian.math@gmail.com
Jian LIU(刘健)
College of Teacher Education,Quzhou University,Quzhou 324000,China
E-mail:liujian.maths@gmail.com

AbstractIn this paper,we investigate the free boundary value problem(FBVP)for the cylindrically symmetric isentropic compressible Navier-Stokes equations(CNS)with densitydependent viscosity coeffi cients in the case that across the free surface stress tensor is balanced by a constant exterior pressure.Under certain assumptions imposed on the initial data,we prove that there exists a unique global strong solution which tends pointwise to a non-vacuum equilibrium state at an exponential time-rate as the time tends to in finity.

Key wordscylindrically symmetric Navier-Stokes equations;free boundary value problem; density-dependent viscosity coeffi cients;strong solution

2010 MR Subject Classification 35Q35;76N03

∗Received October 26,2014;revised December 12,2014.The research of R.X.Lian is supported by NNSFC(11101145),China Postdoctoral Science Foundation(2012M520360),Doctoral Foundation of North China University of Water Sources and Electric Power(201032),Innovation Scientists and Technicians Troop Construction Projects of Henan Province.The research of J.Liu is supported by NNSFC(11326140 and 11501323),the Doctoral Starting up Foundation of Quzhou University(BSYJ201314 and XNZQN201313).

1 Introduction

In this paper,we consider the free boundary value problem to the N-dimensional isentropic compressible Navier-Stokes equations with density-dependent viscosity coefficients.In general,the N-dimensional isentropic compressible Navier-Stokes equations with density-dependent viscosity coeffi cients reads as

where t∈(0,+∞)is the time and x=(x1,x2,···,xN)∈RN,N is the spatial coordinate,ρ＞0 and U=(U1,U2,···,UN)denote the density and velocity,respectively.Pressure function is taken as P(ρ)=ργwith γ＞1,and

is the strain tensor and h(ρ),g(ρ)are theviscosity coeffi cients satisfying

There are many important results made on the compressible Navier-Stokes equations with density-dependent viscosity coeffi cients.Such as,the mathematical derivations were achieved in the simulation of fl ow surface in shallow region[1,2].The prototype model is the physical model of the viscous Saint-Venant system(corresponding to(1.1)with P(ρ)=ρ2,h(ρ)=ρ and g(ρ)=0).The existence of solutions for the 2D shallow water equations was investigated by Bresch and Desjardins[3,4].The well-posedness of solutions to the free boundary value problem with initial finite mass and the fl ow density being connected with the in finite vacuum either continuously or via jump discontinuity was considered by many authors,refer to[5-16]and references therein.The global existence of classical solutions for α∈(0,1/2)was shown by Mellet and Vasseur[17].The qualitative behaviors of global solutions and dynamical asymptotics of vacuum states were also addressed,such as the finite time vanishing of finite vacuum or asymptotical formation of vacuum in large time,the dynamical behaviors of vacuum boundary,the large time convergence to rarefaction wave with vacuum,and the stability of shock profile with large shock strength,refer to[18-22]and references therein.

In addition,some important progress was made about free boundary value problems for multi-dimensional compressible viscous Navier-Stokes equations with constant viscosity coefficients for either barotropic or heat-conducive fluids by many authors,such as,in the case that across the free surface stress tensor is balanced by a constant exterior pressure and/or the surface tension,classical solutions with strictly positive densities in the fl uid regions to FBVP for CNS(1.1)with constant viscosity coeffi cients were proved locally in time for either barotropic flows[23-25]or heat-conductive flows[26-28].In the case that across the free surface the stress tensor is balanced by surface tension[29],exterior pressure[25],or both surface tension and exterior pressure[30]respectively,as the initial data is assumed to be near to non-vacuum equilibrium state,the global existence of classical solutions with small amplitude and positive densities in fl uid region to the FBVP for CNS(1.1)with constant viscosity coeffi cients were obtained.Global existence of classical solutions to FBVP for compressible viscous and heatconductive fluids were also established with the stress tensor balanced by the surface tension and/or exterior pressure across the free surface,refer to[31,32]and references therein.

Recently,there are many signi fi cant progresses achieved on the cylindrically symmetric compressible Navier-Stokes equations.As viscosities both are constants,Frid and Shelukhin[33,34]proved the uniqueness of the weak solution under certain condition.Fan and Jiang[35]showed the global existence of weak solutions.Jiang and Zhang[36]obtained the existence of strong solutions for non-isentropic case.When h(ρ)=ρα,0≤α≤γ,and g(ρ)is a positive constant,Yao,Zhang and Zhu[37]showed the global existence for the cylindrically symmetric solution to compressible Navier-Stokes equations.

In this paper,we consider the free boundary value problem(FBVP)for the cylindrically symmetric isentropic compressible Navier-Stokes equations with density-dependent viscosity coeffi cients in the case that across the free surface stress tensor is balanced by a constant exterior pressure,and focus on the existence and dynamical behaviors of global strong solution,etc.As γ＞1,we show that the free boundary value problem admits a unique global strong solution which tends pointwise to a non-vacuum equilibrium state at an exponential time-rate as the time tends to in finity(refer to Theorem 2.1 for details).

The rest part of the paper is arranged as follows.In Section 2,the main results about the existence and dynamical behaviors of global strong solution for compressible Navier-Stokes equations are stated.Then,some important a priori estimates will be given in Section 3 and the theorem is proven in Section 4.

2 Main Results

For simplicity,we will take h(ρ)=ραand g(ρ)=(α−1)ραand D(U)=∇U in(1.1).The isentropic compressible Navier-Stokes equations become

We are concerned with the cylindrically symmetric solutions of the system(2.1)in a cylindrically symmetric domain between two circular coaxial cylinders.To this end,we denote that

where u(r,t),v(r,t),w(r,t)are radial,angular,and axial velocities respectively,which leads to the following system of equations for r＞0,

where t∈(0,+∞)and r∈Ωt:={r|0＜r−≤r≤r(t)},where r−is a positive constant,and r(t)is a free boundary and de fined assupplemented with the initial data and boundary conditions

where the positive constant peis the exterior pressure and the initial data satisfies

Next,we denote

and de fi ne that

and

then,we give the main results as follows.

with c＞0 a constant independent of time.

If it further holds that(u0,v0,w0)∈H2([r−,r0]),then(ρ,u,v,w)satisfies

The solution(ρ,u)tends to the non-vacuum equilibrium state exponentially

where C1and C2are positive constants independent of time.

Remark 2.2Theorems 2.1 holds for Saint-Venant model for shallow water,i.e.,γ=2 and α=1.

Remark 2.3The initial constraintdoes not always require that the perturbation of the initial data around the equilibrium state(¯ρ,0)is small.Indeed,it can be large provided that the state¯ρ＞0 is large enough.

3 The a Priori Estimates

It is convenient to make use of the Lagrange coordinates in order to establish the a priori estimates.De fi ne the Lagrange coordinates transform

Since the conservation of total mass holds

the boundaries r=r(t)are transformed into x=1,and the domain[r−,r(t)]is transformed into[0,1].The relation between Lagrangian and Eulerian coordinates are satis fied as

The FBVP(2.3)and(2.4)is reformulated into

where the initial data satisfies

and the consistency between initial data and boundary condition holds.

Next,we will deduce the a priori estimates for the solution(ρ,u,v,w)to the FBVP(3.4).To obtain the a priori estimates,we assume a priori that there are constants ρ±＞0 so that

Lemma 3.1Let T＞0.Under the assumptions of Theorem 2.1,it holds for any strong solution(ρ,u,v,w)to the FBVP(3.4)that

ProofTaking the product of(3.4)2,(3.4)3and(3.4)4with ru,rv,w respectively,integrating on[0,1],and using(3.4)1and(3.4)5,we have

which leads to(3.7)after the integration with respect to τ∈[0,T].

Lemma 3.2Let T＞0.Under the assumptions of Theorem 2.1,it holds for any strong solution(ρ,u,v,w)to the FBVP(3.4)that

ProofDi ff erentiating(3.4)1with respect to x,rewriting it in the following form

and substituting(3.10)into(3.4)2,we have

Taking the product of(3.12),(3.4)3and(3.4)4with(u+r(ρα)x),rv,w respectively and integrating on[0,1],and using(3.4)1and boundary conditions,we have

Applying equations(3.4)1and boundary condition,it holds that

which implies

From(3.6),we can find

It holds from(3.6),(3.7),(3.15)and(3.16)that

Integrating(3.13)with respect to τ∈[0,T]and using(3.17),we can complete the proof of(3.9).

Lemma 3.3Let T＞0.Under the assumptions of Theorem 2.1,it holds

where ρ∗and ρ∗are positive constants independent of time.

ProofDenote

and

It is easy to verify that ϕ(ρ)≥0 and ψ′(ρ)≥0.In addition,it holds as ρ→+∞that

and as ρ→0 that

It follows from(3.7)and(3.9)

From the condition

we can find that there are two positive constants ρ∗and ρ∗independent of time and choose

such that

Lemma 3.4Let T＞0.Under the assumptions of Theorem 2.1,it holds for any strong solution(ρ,u,v,w)to the FBVP(3.4)that

where C＞0 denotes a constant independent of time.

ProofMultiplying(3.4)2by ρ−(1+α)(ru)τand integrating the result with respect to x over[0,1],making use of the boundary conditions,we obtain

which implies

From(3.4)2,(3.7),(3.9)and(3.19),we can deduce that

where C denotes a constant independent of time.Use(3.32)and(3.33),we can obtain that

which together with(3.4)2implies

Using the similar methods we can obtain the following

and

The combination of(3.35)-(3.37)gives(3.29).

Lemma 3.5Let T＞0.Under the assumptions of Theorem 2.1,it holds for any strong solution(ρ,u,v,w)to the FBVP(3.4)that

where C＞0 denotes a constant independent of time.

ProofDi ff erentiating(3.4)2with respect to τ,multiplying the result by(ru)τand integrating the result with respect to x over[0,1],we have

A complicated computation gives

and by means of Gronwall’s inequality,(3.4)2,(3.7),(3.9),(3.19)and(3.29),it holds that

where C denotes a constant independent of time,from(3.41),we can find

Using the similar methods we can obtain the following

and

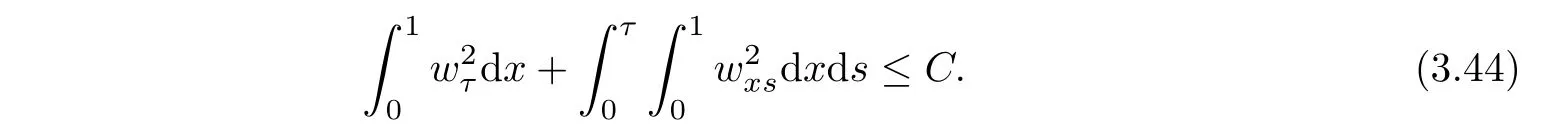
We can complete the proof of Lemma 3.5.

Lemma 3.6Let T＞0.Under the assumptions of Theorem 2.1,it holds for any strong solution(ρ,u,v,w)to the FBVP(3.4)that

where C1and C2denote two positive constants independent of time.

ProofApplying(3.8)and(3.13)with modi fi cation,we can obtain

and

It holds from Gagliardo-Nirenberg-Sobolev inequality,(3.7),(3.9)and(3.19)that

and

where C and C are positive constants independent of time.

Denote

By(3.46)-(3.49),a complicated computation gives rise to

where C0≤C is a positive constant independent of time.From(3.50),we have

By the fact

where c＞0 is a constant independent of time,and Gagliardo-Nirenberg-Sobolev inequality

we can deduce(3.45).?

4 Proof of Main Results

ProofThe global existence of unique strong solution to the FBVP(2.3)and(2.4)can be established in terms of the short time existence carried out as in[7],the uniform a priori estimates and the analysis of regularities,which indeed follow from Lemmas 3.1-3.5.We omitthe details.The large time behaviors follow from Lemma 3.6 directly.The proof of Theorem 2.1 is completed.

AcknowledgementsThe authors are grateful to Professor Hai-Liang Li for his helpful discussions and suggestions about the problem.

References

[1]Gerbeau J F,Perthame B.Derivation of viscous Saint-Venant system for laminar shallow water,Numerical validation.Discrete Contin Dyn Syst Ser B,2001,(1):89-102

[2]Marche F.Derivation of a new two-dimensional viscous shallow water model with varying topography,bottom friction and capillary effects.European J Mech B/Fluids,2007,26:49-63

[3]Bresch D,Desjardins B.Existence of global weak solutions for a 2D viscous shallow water equations and convergence to the quasi-geostrophic model.Comm Math Phys,2003,238:211-223

[4]Bresch D,Desjardins B.On the construction of approximate solutions for the 2D viscous shallow water model and for compressible Navier-Stokes models.J Math Pures Appl,2006,86:362-368

[5]Fang D Y,Zhang T.Global solutions of the Navier-Stokes equations for compressible fl ow with densitydependent viscosity and discontinuous initial data.J Di ff er Equ,2006,222:63-94

[6]Guo Z H,Li H L,Xin Z P.Lagrange structure and dynamics for solutions to the spherically symmetric compressible Navier-Stokes equations.Commun Math Phys,2012,309:371-412

[7]Jiang S,Xin Z P,Zhang P.Global weak solutions to 1D compressible isentropy Navier-Stokes with densitydependent viscosity.Methods Appl Anal,2005,12:239-252

[8]Lian R X,Guo Z H,Li H L.Dynamical behaviors of vacuum states for 1D compressible Navier-Stokes equations.J Di ff er Equ,2010,248:1926-1954

[9]Liu J.Local existence of solution to free boundary value problem for compressible Navier-Stokes equations.Acta Mathematica Scientia,2012,32B(4):1298-1320

[10]Liu J,Lian R X.Global existence of the cylindrically symmetric strong solution to compressible Navier-Stokes equations.Abs Appl Anal,2014,2014:1-8

[11]Liu T P,Xin Z P,Yang T.Vacuum states for compressible fl ow.Discrete Contin Dynam Systems,1998,1998:1-32

[13]Vong S W,Yang T,Zhu C J.Compressible Navier-Stokes equations with degenerate viscosity coeffi cient and vacuum II.J Di ff er Equ,2003,192:475-501

[14]Yang T,Yao Z A,Zhu C J.Compressible Navier-Stokes equations with density-dependent viscosity and vacuum.Comm Partial Di ff er Equ,2001,26:965-981

[15]Yang T,Zhao H.A vacuum problem for the one-dimensional compressible Navier-Stokes equations with density-dependent viscosity.J Di ff er Equ,2002,184:163-184

[16]Yang T,Zhu C J.Compressible Navier-Stokes equations with degenerate viscosity coeffi cient and vacuum.Commu Math Phys,2002,230:329-363

[17]Mellet A,Vasseur A.Existence and uniqueness of global strong solutions for one-dimensional compressible Navier-Stokes equations.SIAM J Math Anal,2008,39:1344-1365

[18]Guo Z H,Jiu Q S,Xin Z P.Spherically symmetric isentropic compressible flows with density-dependent viscosity coeffi cients.SIAM J Math Anal,2008,39:1402-1427

[19]Jiu Q S,Wang Y,Xin Z P.Stability of rarefaction waves to the 1D compressible Navier-Stokes equations with density-dependent viscosity.Comm Partial Di ff er Equ,2011,36:602-634

[20]Jiu Q S,Xin Z P.The Cauchy problem for 1D compressible flows with density-dependent viscosity coefficients.Kinet Relat Modeks,2008,1:313-330

[21]Li H L,Li J,Xin Z P.Vanishing of vacuum states and blow-up phenomena of the compressible Navier-Stokes equations.Commu Math Phys,2008,281:401-444

[22]Lian R X,Liu J,Li H L,Xiao L.Cauchy problem for the one-dimensional compressible Navier-Stokes equations.Acta Mathematica Scientia,2012,32B(1):315-324

[23]Solonnikov V A,Tani A.Free Boundary Problem for a Viscous Compressible Flow with a Surface Ten-sion//Constantin Carathéodory:an International Tribute,Vol I,II.Teaneck,NJ:World Sci Publ,1991:1270-1303

[24]Zajaczkowski W M.Existence of local solutions for free boundary problems for viscous compressible barotropic fluids.Ann Polon Math,1995,60:255-287

[25]Zajaczkowski W M.On nonstationary motion of a compressible barotropic viscous fl uid bounded by a free surface.Dissert Math,1993,324:1-101

[26]Secchi P,Valli A.A free boundary problem for compressible viscous fluids.J Reine Angew Math,1983,341:1-31

[27]Tani A.On the free boundary value problem for compressible viscous fl uid motion.J Math Kyoto Univ,1981,21:839-859

[28]Zadrzy´nska E,Zajaczkowski W M.On local motion of a general compressible viscous heat conducting fl uid bounded by a free surface.Ann Polon Math,1994,59:133-170

[29]Solonnikov V A,Tani A.Evolution free boundary problem for equations of motion of viscous compressible barotropic liquid//The Navier-Stokes Equations II-Theory and Numerical Methods(Oberwolfach,1991).Lecture Notes in Math,1530.Berlin:Springer,1992:30-55

[30]Zajaczkowski W M.On nonstationary motion of a compressible barotropic viscous capillary fl uid bounded by a free surface.SIAM J Math Anal,1994,25:1-84

[31]Zadrzy´nska E.Evolution free boundary problem for equations of viscous compressible heat-conducting capillary fluids.Math Meths Appl Sci,2001,24:713-743

[32]Zadrzy´nska E,Zajaczkowski W M.On the global existence theorem for a free boundary problem for equations of a viscous compressible heat conducting capillary fl uid.J Appl Anal,1996,2:125-169

[33]Frid H,Shelukhin V V.Boundary layer for the Navier-Stokes equations of compressible fluids.Commun Math Phys,1999,208:309-330

[34]Frid H,Shelukhin V V.Vanishing shear viscosity in the equations of compressible fluids for the flows with the cylinder symmetry.SIAM J Math Anal,2000,31:1144-1156

[35]Fan J S,Jiang S.Zero shear viscosity limit for the Navier-Stokes equations of compressible isentropic fluids with cylindric symmetry.Rend Sem Mat Univ Politec Torino,2007,65:35-52

[36]Jiang S,Zhang J W.Boundary layers for the Navier-Stokes equations of compressible heat-conducting fi ows with cylindrical symmetry.SIAM J Math Anal,2009,41:237-268

[37]Yao L,Zhang T,Zhu C J.Boundary layers for compressible Navier-Stokes equations with density-dependent viscosity and cylindrical symmetry.Ann Inst H Poincaré Anal Non Linéaire,2011,28:677-709