ON POINTS CONTAIN ARITHMETIC PROGRESSIONS IN THEIR LÜROTH EXPANSION∗
Zhenliang ZHANG(张振亮)School of Mathematical Sciences,Henan Institute of Science and Technology,Xinxiang 453003,China;School of Mathematics and Statistics,Huazhong Universitry of Science and Technology,Wuhan 430074,ChinaE-mail:zhliang zhang@hotmail.comChunyun CAO(曹春云)College of Science,Huazhong Agricultural Universitry,Wuhan 430070,ChinaE-mail:caochunyun@mail.hzau.edu.cn
ON POINTS CONTAIN ARITHMETIC PROGRESSIONS IN THEIR LÜROTH EXPANSION∗
Zhenliang ZHANG(张振亮)
School of Mathematical Sciences,Henan Institute of Science and Technology,
Xinxiang 453003,China;
School of Mathematics and Statistics,Huazhong Universitry of Science and Technology,
Wuhan 430074,China
E-mail:zhliang zhang@hotmail.com
Chunyun CAO(曹春云)†
College of Science,Huazhong Agricultural Universitry,Wuhan 430070,China
E-mail:caochunyun@mail.hzau.edu.cn
AbstractFor any x∈(0,1](except at most countably many points),there exists a unique sequence{dn(x)}n≥1of integers,called the digit sequence of x,such that

The dexter in finite series expansion is called the Lüroth expansion of x.This paper is concerned with the size of the set of points x whose digit sequence in its Lüroth expansion is strictly increasing and contains arbitrarily long arithmetic progressions with arbitrary common di ff erence.More precisely,we determine the Hausdor ff dimension of the above set.
Key wordsLüroth expansion;arithmetic progression;Hausdor ff dimension
2010 MR Subject Classi fi cation11K55;28A80
∗Received September 15,2014;revised March 6,2015.This work was supported by NSFC(11326206,11426111).
†Corresponding author:Chunyun CAO.
1 Introduction
The Lüroth expansion was first introduced by Lüroth[1]in 1883.For any x∈(0,1],the Lüroth map T:(0,1]→(0,1]is de fined by

Then we de fi ne the integer sequence
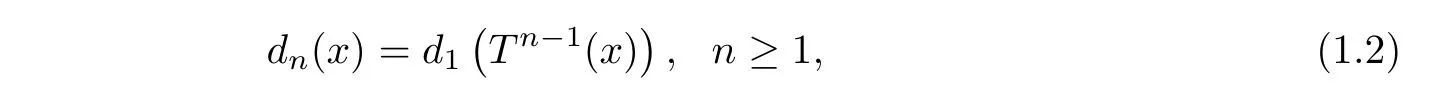
where Tndenotes the nth iterate of T(T0=Id(0,1]).
By algorithm(1.1)and(1.2),any x∈(0,1](except at most countably many points)can be developed uniquely into an in finite series expansion of the form

which is called the Lüroth expansion of x and denote it by x=[d1(x),d2(x),···,dn(x),···]for short.
The above algorithm implies dn≥2 for all n≥1.On the contrary,for a sequence of integers{dn}n≥1satisfying dn≥2,∀n≥1,there exists a unique x∈(0,1]such that dn(x)=dn,∀n∈N in the Lüroth expansion of x.Namely,each irrational x∈(0,1]is corresponding to an in finite integer sequence{dn}n≥1.
Whether integer subset contains arbitrarily long arithmetic progressions is a long-standing question in number theory,especially for some peculiar subsets,such as primes.For this,Van der Waerden[2]in 1927 established that while the set of integers is arbitrarily partitioned into two classes,at least one class contains arbitrarily long arithmetic progressions.In 2008,Green and Tao[3]gave a a ffi rmative answer to the problem that the primes contain arbitrarily long arithmetic progressions.
Since{dn}n≥1can assume arbitrarily large values,it is possible that there are points whose sequence of digits in its Lüroth expansion contains arbitrarily long arithmetic progressions.In this paper,we discuss the above long-standing question in the setting of Lüroth expansion in the view of metric number theory.To be speci fi c,we are interested in the set of points whose sequence of digits in its Lüroth expansion is strictly increasing and contains arbitrarily long arithmetic progressions.Denote such a set by ES,i.e.,

Furthermore,we care about the points whose sequence of digits in its Lüroth expansion contains the arithmetic progressions with arbitrary common di ff erence as well as satisfying above properties.More precisely,we consider the set EASde fined as follows:

It is natural to ask how large such sets are in the sense of Lebesgue measure or Hausdor ff dimension.We prove that
The growth speed of the digit sequence{dn(x)}n≥1was studied in[4].The metric and ergodic properties of the digit sequence{dn(x)}n≥1and the Lüroth map T de fined by(1.1)were extensively studied in[5](see also[6-11]).The behavior of approximating real numbers by Lüroth expansion was thoroughly investigated in[12-14].Since the Lüroth system can also be viewed as an in finite iterated function system,dimensional theory in Lüroth expansionis also attached great importance.The spectrum analysis of the frequency of the digits was given in[15,16].Especially in[17],they showed that the set of numbers with bounded Lüroth expansions(or bounded Lüroth series)is winning and strong winning,which implies that the set of full Hausdor ff dimension may contain no such numbers considered in this paper.
2 Proof of Theorem 1.1
In this section,we prove the main result of this note.Let us first fi x some notations and briefly recall some basic properties and known results of Lüroth expansion.
For any n≥1 and dj≥2,1≤j≤n,call(d1,d2,···,dn)an admissible block of order n.For any n≥1,denote by Lnthe collection of all admissible blocks of order n,i.e.,

For any(d1,d2,···,dn)∈ Ln,let

where cl denotes the closure of a set.It is clear that In(d1,d2,···,dn)is a subinterval of(0,1],and from the algorithm(1.1),its length is given by the following formula.
In order to compute the Hausdor ff dimension of the set ES,we recall a result of Shen which will be used later to estimate the upper bound of dimHES.
Lemma 2.2(see[4])dimH{x∈[0,1):dn(x)→∞as n→∞}=12.
We also need the following lemma(usually called Billingsley’s theorem),which is an important tool to obtain a lower bound on the Hausdor ff dimension in fractal geometry.
Lemma 2.3(see[18])Let E⊂(0,1]be a Borel set andµis a measure withµ(E)>0.If for any x∈E,

where B(x,r)is the ball with center x and radius r,then

Now let us begin the proof of Theorem 1.1.
The upper bound on dimHESis easily available from Lemma 2.2 by noting that{dn(x)}n≥1is strictly increasing implies that dn(x)→∞as n→∞.That is,

To determine the lower bound of dimHEAS,for any integer α>2,we will first construct a proper set E(α)such that for any x∈E(α),the digit sequence of x is strictly increasing.Moreover,the Hausdor ff dimension of E(α)is approximate to12with the increase of α.From this springboard set,we construct a subset of the target set EASby inserting a group of arithmetic progressions at the appropriate positions in the digit sequences of the points in E(α).By the appropriate choice of the positions,we will find a Hölder function between this subset and E(α).The above idea has been applied successfully in[19,20].
Lemma 2.4Let α≥2 be an integer,denote

Then

ProofIn order to estimate the Hausdor ff dimension of E(α),we shall make use of a kind of symbolic space described as follows.For any n≥1,set

For each n≥1 and(d1,d2,···,dn)∈Dn,we call In(d1,d2,···,dn)an admissible cylinder of order n with respect to E(α).Then

Now we construct a set functionµon admissible cylinder by:µ(I)=1 and for any n≥1,

By the Carathéodory extension theorem,µcan be extended to a probability measure supported on E(α).
In light of Billingsley’s theorem,we are required to check the above de fined measureµ satisfies(2.1)for all x∈E(α).For each x∈E(α),there exists a sequence{dn}n≥1such that for each n≥1,x∈In(d1,d2,···,dn)and(d1,d2,···,dn)∈Dn.For any 0<r<18,there exists n≥1 such that
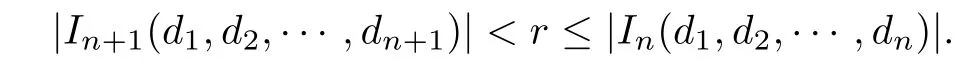
Note that for any adjacent admissible cylinders of order n with respect to E(α):I(d1,···,dn)and I(d1,···,dn+1),we have

since dn>(2n)α≥4.Then B(x,r)can intersect at most fi ve nth order admissible cylinders and at least one(n+1)th order admissible cylinder.As a result,we have
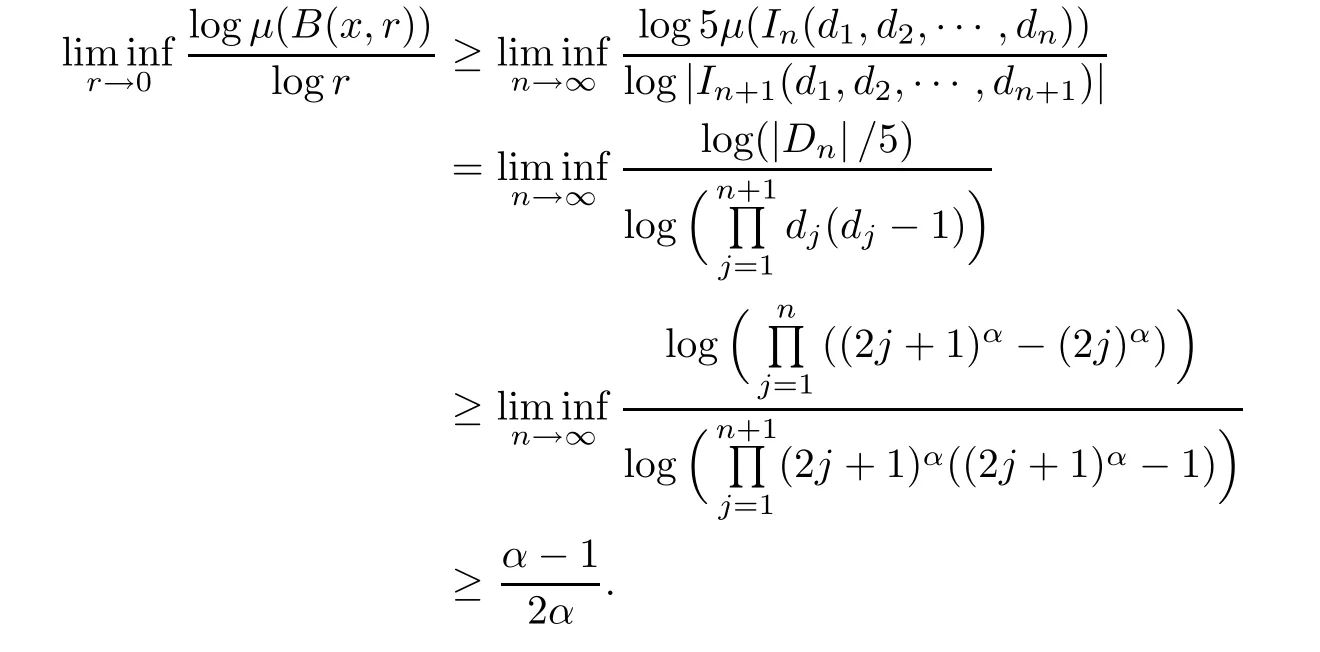
By Lemma 2.1,the proof is completed.
From this springboard set,now we turn to construct points of EAS.For any l≥1 and d≥1,let Ldl={d,2d,···,ld}be an arithmetic progression with length l and common di ff erence d.Put


The new arranged sequence is denoted by{Lk}k≥1.It is easy to observe that,for any k≥1,

where maxLkdenotes the maximum of Lk.Without any confusion,Lkis considered as a vector with its elements arranged in increasing order.
For every x∈E(α),we will construct a point y belonging to EAS.For this purpose,the strategy is to insert vectors Lk+dnk(x)at the position nk(to be chosen)of the digit sequence of Lüroth expansion of x.More precisely,let{nk}k≥0be a sequence of integers such that
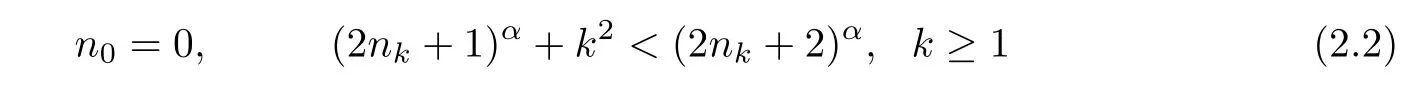
and

For each x∈E(α),we construct the point y as follows.
For 1≤n≤n1,set dn(y)=dn(x).
For n≤n1+|L1|,set(dn1+1(y),···,dn1+|L1|(y))=dn1(x)+L1.
For n>n1+|L1|,let k≥1 be the integer such that

Then as above,
For nk+|L1|+···+|Lk|<n≤nk+1+|L1|+···+|Lk|,set

For nk+1+|L1|+···+|Lk|<n≤nk+1+|L1|+···+|Lk+1|,set

By the construction,it is evident that arbitrarily long arithmetic progressionswith arbitrary common di ff erence occur in the sequence{dn(y)}n≥1.Besides,from condition(2.2)satis fied by the sequence{nk}k≥0and the fact maxLk≤k2,the sequence{dn(y)}n≥1is also strictly increasing.So,we conclude that y∈EAS.We call x the seed of y and denote by FS(α)the collection of points constructed in the above way,then we have

Now we establish a connection between FS(α)and E(α)by means of a(1+∈)−1-Hölder function.Note that(2.3),for any∈>0,we can choose k0large enough such that for everyn≥nk0and k≥k0,
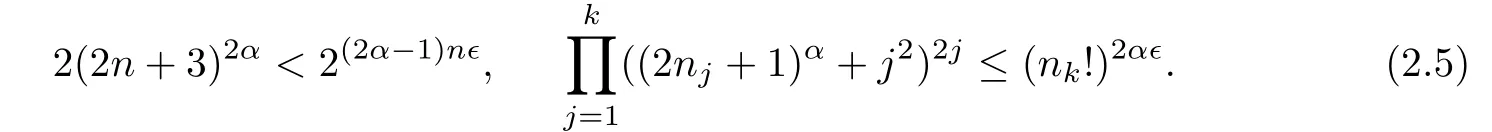
Fix d1,d2,···,dnk0with(2j)α≤dj≤(2j+1)αfor 1≤j≤nk0.Let
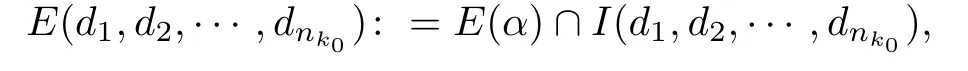
and denote by FS(d1,d2,···,dnk0)the corresponding set of points y whose seed belongs to the set E(d1,d2,···,dnk0).
Now we de fi ne a map

where x is the seed of y.It is easy to find the map f is bijective.What is more,we will claim the map f is(1+∈)−1−Hölder function.For any pair y1,y2∈FS(d1,d2,···,dnk0),let x1,x2be the seeds of y1and y2,respectively.Denote by¯n the smallest integer such thatThenAssume that
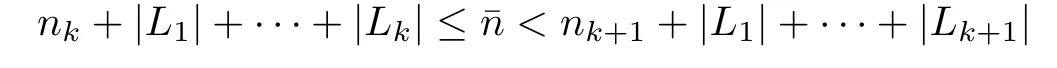
for some k≥k0.Recall that if x is the seed of y,then for nk+1+|L1|+···+|Lk|<n≤nk+1+|L1|+···+|Lk+1|,
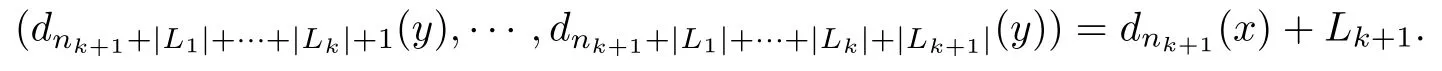
Therefore,for any nk+1+|L1|+···+|Lk|≤n<nk+1+|L1|+···+|Lk+1|,if dn(y1)=dn(y2),then dnk+1(x1)=dnk+1+|L1|+···+|Lk|(y1)=dnk+1+|L1|+···+|Lk|(y2)=dnk+1(x2).So dn+1(y1)=
dn+1(y2).By the de finition of¯n,we only need to consider the case

First of all,we estimate the gap between y1and y2.Without loss of generality,assume thatis on the left

Thus,

Combining this with
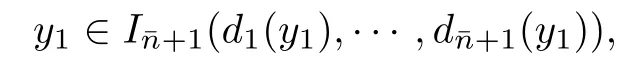
we can obtain that the gap between y1and y2is greater than the distance between the right endpoint ofHence

since α≥2 and nk∈N.
Next,we estimate the gap between x1and x2.Recall thatnk+1+|L1|+···+|Lk|,we have

So,by Lemma2.1,
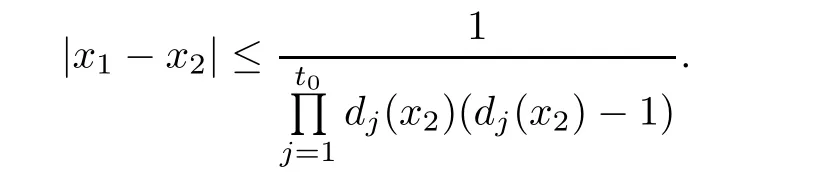
Noticing that

and

By(2.5)we have

So,the map f is(1+∈)−1-Hölder function.Then

for any(d1,d2,···,dnk0)∈Dnk0.Since

and∈is arbitrary,we get

By Lemma 2.4 and let α→∞,then we can get
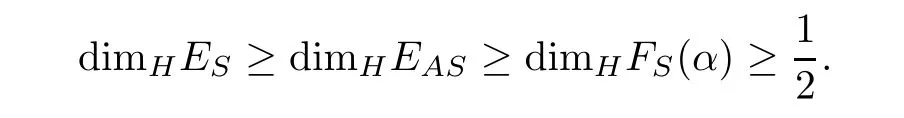
AcknowledgementsThe authors are grateful to Professor J.Wu for many helpful advices.
References
[1]Lüroth J.Ueber eine eindeutige entwickelung von zahlen in eine unendliche reihe.Math Ann,1883,21:411-423
[2]Van der Waerden B L.Beweis einer Baudetschen Vermutung.Nieuw Arch Wisk,1927,15:212-216
[3]Green B,Tao T.The primes contain arbitrarily long arithmetic progressions.Ann Math,2008,167:481-547
[4]Shen L M,Fang K.The fractional dimensional theory in Lüroth expansion.Czech Math J,2011,61:795-807
[5]Dajani K,Kraaikamp C.Ergodic Theory of Numbers.The Carus Mathematical Monographs 29.Washigton D C:Mathematical Association of America,2002
[6]Galambos J.Representations of Real Numbers by In finite Series.Lecture Notes in Mathematical 502.Berlin:Springer,1976
[7]Jager H,de Vroedt C.Lüroth series and their ergodic properties.Nederl Akad Wet,Proc,Ser,1969,72:31-42
[8]Kesseböhmer M,Munday S,Stratmann B O.Strong renewal theorems and Lyapunov spectra for α-Farey and α-Lüroth systems.Ergodic Theory Dyn Syst,2012,32:989-1017
[9]Shen L M,Liu Y H,Zhou Y Y.A note on a problem of J.Galambos.Turkish J Math,2008,32:103-109
[10]Šalát T.Zur metrischen theorie der Lürothschen Entwicklungen der reellen Zahlen.Czech Math J,1968,18:489-522
[11]Wang S K,Xu J.On the Lebesgue measure of sum-level sets for Lüroth expansion.J Math Anal Appl,2011,374:197-200
[12]Barrionuevo J,Burton R M,Dajani K,Kraaikamp C.Ergodic properties of generalized Lüroth series.Acta Arith,1996,74:311-327
[13]Cao C Y,Wu J,Zhang Z L.The e ffi ciency of approximating the reals by Lüroth expansion.Czech Math J,2013,63:497-513
[14]Dajani K,Kraaikamp C.On approximation by Lüroth series.J Théor Nombres Bordeaux,1996,8:331-346
[15]Barreiraa L,Iommi G.Frequency of digits in the Lüroth expansion.J Number Theory,2009,129:1479-1490
[16]Fan A H,Liao L M,Ma J H,Wang B W.Dimension of Besicovitch-Eggleston sets in countable symbolic space.Nonlinearity,2010,23:1185-1197
[17]Mance B,Tseng J.Bounded Lüroth expansions:applying Schmidt games where in finite distortion exists.Acta Arith,2013,158:33-47
[18]Falconer K J.Techniques in Fractal Geometry.Chichester:John Wiley&Sons,1997
[19]Hu D G,Hu X H.Arbitrarily long arithmetic progressions for continued fractions of laurent series.Acta Math Sci,2013,33B(4):943-949
[20]Tong X,Wang B W.How many points contain arithmetic progressions in their continued fraction expansion? Acta Arith,2009,139:369-376
 Acta Mathematica Scientia(English Series)2016年1期
Acta Mathematica Scientia(English Series)2016年1期
- Acta Mathematica Scientia(English Series)的其它文章
- SEVERAL UNIQUENESS THEOREMS OF ALGEBROID FUNCTIONS ON ANNULI∗
- GENERAL ALGEBROID FUNCTION AND ITS APPLICATION∗
- CONVERGENCE RATE OF SOLUTIONS TO STRONG CONTACT DISCONTINUITY FOR THE ONE-DIMENSIONAL COMPRESSIBLE RADIATION HYDRODYNAMICS MODEL∗
- SECONDARY CRITICAL EXPONENT AND LIFE SPAN FOR A DOUBLY SINGULAR PARABOLIC EQUATION WITH A WEIGHTED SOURCE∗
- EXISTENCE AND UNIQUENESS OF PERIODIC SOLUTIONS FOR GRADIENT SYSTEMS IN FINITE DIMENSIONAL SPACES∗
- BLOW-UP OF CLASSICAL SOLUTIONS TO THE COMPRESSIBLE MAGNETOHYDRODYNAMIC EQUATIONS WITH VACUUM∗
