对数函数及其性质的应用探讨研究

常　梅　姜铁军（大庆市第五十六中学）



对数函数及其性质的应用探讨研究

常梅姜铁军
（大庆市第五十六中学）

摘要：理解对数函数的概念和意义，掌握对数函数定义域、值域的求法，能画出具体对数函数图像，并能根据对数函数的图像说明对数函数的性质，掌握对数函数的单调性，会进行同底对数和不同底对数大小的比较。通过指数函数、对数函数的学习，加深理解分类讨论、数形结合这两种重要数学思想的意义和作用。

关键词：对数函数；性质；图像

探究一：对数函数有关的定义域、值域

例1.求下列函数的定义域

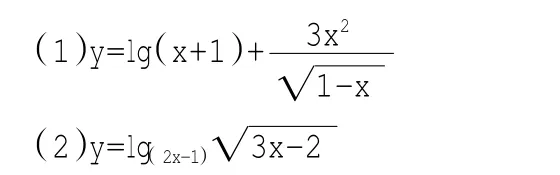
方法归纳：

1.求与对数函数有关的函数定义域时应遵循的原则：分母不能为0，根指数为偶数时，被开方数非负，对数的真数大于0，底数大于0且不为1。

2.求函数定义域的步骤：列出使函数有意义的不等式组，化简并解出自变量的取值范围，确定函数的定义域。

（3）函数y=2+log2x（x≥1）的值域为（C）

A.（2，+∞）B.（-∞，2）C.［2，+∞）D.［3，+∞）

方法点拨：可以直接利用对数函数的单调性求出函数的值域，也可以借助对数函数的图像求出函数的值域，更加直观、形象。

探究二：对数型函数单调性的应用（重点）

例2.比较下列各组对数值的大小

（1）log3.10.5与log3.10.2

（3）log25与log35

（4）log56与log65

（5）loga3.2与loga3.7（a>0，且a≠1）

方法归纳：

对数值大小的比较方法有：

1.如果底数相同，真数不同，直接利用同一个对数函数的单调性来比较大小，如果底数为字母，则要分类讨论。

2.如果底数不同，真数相同，可以利用图像的高低与底数的大小关系解决，或利用换底公式化为同底的再进行比较。

3.若底数、真数都不相同，则常借助中间量1，0，-1等进行比较。

例3.复合函数单调性的判断及应用

A.在R上是增函数

B.在R上是减函数

方法点拨：

求复合函数单调区间的步骤：

1.求出函数的定义域。

2.将复合函数分解为基本初等函数。

3.确定各基本初等函数的单调性及单调区间。

4.根据复合函数单调性的判断方法求原函数的单调区间。

例4.利用函数单调性求函数值域

函数y=logax（a>0，且a≠1）在［2，4］上的最大值与最小值的差是1，求a的值。

方法点拨：

通过对底数a的讨论来确定此对数函数的单调性，进而可以确定究竟在区间的哪个端点处分别取得最大值和最小值，列出关于a的对数方程，求出a值。

例5.利用函数单调性求解对数不等式

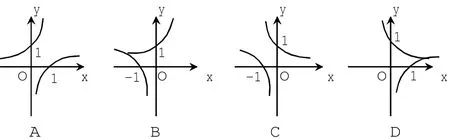
已知log0.7（2x）

解题技巧：解对数不等式应根据对数函数的单调性转化为关于真数的不等式，求解时应注意原对数式的真数大于0的条件，常见对数不等式类型如下：

探究三：对数型函数图像的应用

例6.（1）函数y=loga（x+1）-2（a>0，且a≠1）的图像恒过定点_________。

（2）已知a>0且a≠1，则函数y=ax与y=log（a-x）的图像可能是（B）

对于函数图像的掌握要求两点：首先要求熟悉掌握各种基本初等函数的图像，复杂函数的图像都是由简单函数的图像通过平移、伸缩、对称等变换而得到的。其次把握函数图像的性质，根据图像的性质去判断，如：过定点、定义域、值域、单调性、奇偶性等。

探究四：对数型函数性质的综合应用

例7.已知函数f（x）=loga（x+1）-loga（1-x）（a>0，且a≠1）

（1）求f（x）的定义域；

（2）判断f（x）的奇偶性并予以证明。

解决对数函数综合问题的方法：对数函数常与函数的奇偶性、单调性、最值以及不等式等问题综合，求解中通常会涉及对数运算。解决此类综合问题，首先要将所给的条件进行转化，然后结合涉及的知识，明确各知识点的应用思路、化简方向，与所求目标建立联系，从而找到解决问题的思路。

·编辑鲁翠红