数形结合思想在中学数学解题中的应用

■佳木斯市第三中学刘春雷

数形结合思想在中学数学解题中的应用

■佳木斯市第三中学刘春雷

数形结合思想起源于古希腊，欧几里得的《几何原本》中对此有所提及；十七世纪，笛卡尔建立平面直角坐标系并发表了《几何学》；再后来，费马用代数方法研究几何学，著成《平面与立体轨迹引论》，从此数形结合思想被重视.我国在公元前十五世纪的甲骨文中对数形结合思想也有所记载；大约在公元前二世纪左右，我国已经记载了勾股定理；祖冲之所得π的结果比欧洲早一千年.数形结合思想的应用非常广泛，仍有很大的研究空间.数形结合思想用画图的方法来解决代数问题，用数字、公式来解决几何问题，使代数的繁琐问题变换成图形，更加直观明了，使复杂的图形变换成数字，更加具体化，结果也更加准确.目前国外的课本注重数形结合思想，强调用心理解然后应用，使学生将此思想变成一种习惯与意识，并能够直接运用.而在我国，数形结合思想在课本中体现得很少，基本由教师结合具体题型进行具体分析、传授，只是作为一种有利的解题工具出现.然而，在新课改的背景下，我国的数学教学越来越注重培养学生的数形结合能力，也有越来越多的人开始研究数形结合思想.著名的数学家华罗庚曾经说过：“数与形，本是相倚依，焉能分作两边飞，数无形时少直觉，形无数时难入微，数形结合百般好，隔离分家万事休，切莫忘，几何代数统一体，永远联系莫分离。”罗新兵在文章《数形结合的解题研究——表征的视角》中对该思想大加赞扬，同时也提出高中生存在的普遍现状：往往“以形助数”，在几何问题中通过直角坐标系向量使问题代数化，却往往忽略几何图形本身的定义和性质，这是应该注意的.

本文将从两个方面来研究数形结合思想在解题中的应用：一方面是以形助数，按照中学课本知识的顺序，用几何的方法来对典型例题进行解答；另一方面是以数辅形，利用数学公式来解决几何问题.

一、“以形助数”思想在中学数学解题中的应用

所谓的“以形助数”就是将所给出题目中的文字语言翻译成图形语言，通过仔细研究图形的特点，发现图形中蕴含的数量关系，然后再进行分析计算.

1.“以形助数”在集合问题中的应用

根据集合所涉及的元素的特点，可以利用韦恩图或者数轴来解决.

通常在集合韦恩图中，用长方形来表示全集，用圆来表示集合.集合与集合的关系表现为两圆的位置关系，两个圆相交的意思是有公共的元素，未相交部分为各自的元素，两个圆相交一点说明有一个相同的元素，两个圆相离说明没有相同的元素.

例1全集U={a，b，c，d，e}，如果A∩B={b}，并且（CuA）∩B={d}，（CuA）∩（CuB）={a，e}，则元素c在哪？

解：此题涉及5个集合，用常规方法解题比较复杂，用韦恩图则简单得多.见图1.

A∩B={b}说明b为A，B的公共部分；（CuA）∩B={d}说明d∉A且d∈B；（CuA）∩（CuB）={a，e}说明a，e∉A且a，e∉B，所以c∉B且c∈A，即图中阴影部分.

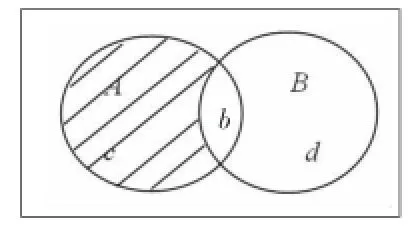
图1

例2某班有60名学生，会跳舞的有30人，会唱歌的有42人，既会唱歌又会跳舞的有14人，既不会跳舞又不会唱歌的有多少人？

解：设U={60名学生}，M={会跳舞的学生}，N={会唱歌的学生}，M∩N={既会跳舞又会唱歌的学生}.见图2.

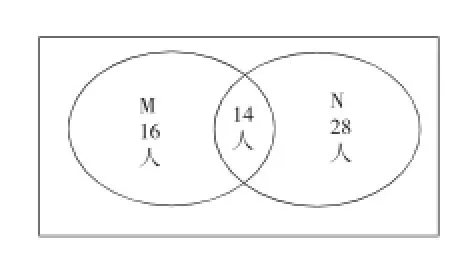
图2

不会唱歌也不会跳舞的学生有60-16-14-28=2人.

当用数轴来解决集合问题时，一般情况下，在数轴上画出几个解，并通过不等号的方向来画出解集，交集即二者的公共部分，无公共部分即没有交集，为空集.

2.“以形助数”在解方程问题中的应用

在中学数学中，方程主要包括两个部分，分别为一元二次方程和二元一次方程，接下来将用“以形助数”法来解决相关方程问题.

一元二次方程的一般式为ax2+bx+c=0，我们可以利用方程图像与坐标轴的位置关系来分析方程解的情况.若方程图像与x轴有两个交点，即该方程有两个不相等的实数根；若方程图像与x轴有一个交点，则说明该方程有两个相等的实数根；若方程图像与x轴没有交点，则该方程在实数域内没有实数根.

例3解方程（3-x）2+x2=5.

解：通过列表描点连线的方法，画出x2-3x+2=0的图像，该方程与x轴相交，有两个交点，坐标分别为（1，0），（2，0）.见图3.

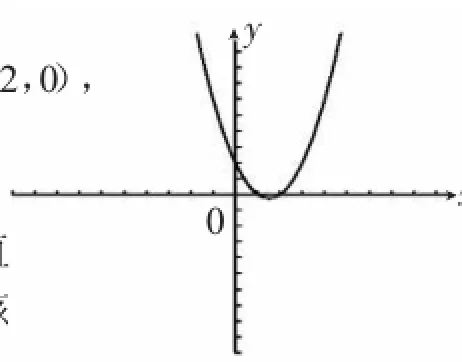
图3

所以方程的解就是（1，0），（2，0），

解：在坐标系上画出两条直线，见图4，两直线平行，所以该方程组没有解.

3.“以形助数”在解不等式问题中的应用

解不等式的时候通常先把不等号换成等号，求出等式的解，然后画出两个函数的图像，依次写出范围内两函数的大小关系，那些满足不等号的即为不等式的解.

例5求（x-1）2＞x中x的取值范围.

解：先求出（x-1）2=x的值为y1=（x-1）2与y2=x的图像，见图5.

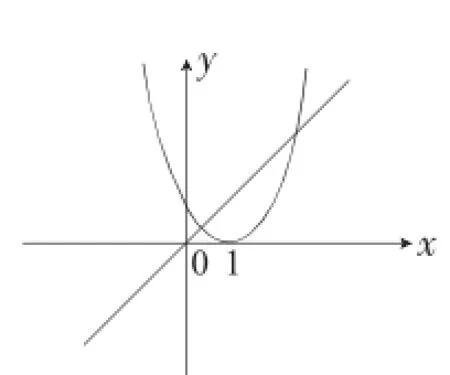
图5

解不等式问题时，可简记口诀：“从上到下，从右到左，奇次根穿过，偶次根穿不过”.

二、“以数辅形”思想在中学数学解题中的应用

“以数辅形”是指在一些几何问题中，运用数与形结合的观点去考虑问题，将形向数转化，从而解决问题.

1.“以数辅形”在平面几何问题中的应用

在解决一些基础图形，如三角形、四边形、圆等复杂的长度和角度的问题时，我们一般利用“以数辅形”思想，借助数学公式来解决.

例6 AB垂直于地面，影子恰好在CD和BC上（见图6），如果CD与水平面成45°，

图6

解：此题有两种解法.

（1）三角形中角和边的公式

做一条辅助的线，延长AD至与水平面交F点，过D点做DE⊥CF，垂足为E.因为∠DCE=45°，∠A=60°，

（2）相似三角形

2.“以数辅形”在立体几何问题中的应用

解决立体几何问题，当无法直接看出点线面之间的关系时，可以用代数向量的方法进行求解，其思路简单，只须建立恰当的直角坐标系，写出每一点的坐标，再根据公式代入求解.

例7 PD⊥正方形ABCD，见图7，AB=2，E平分PB，（1）写出E的坐标；（2）是否存在一点F，使EF⊥平面PCB？

图7

解：（1）以DA、DC、DP为x、y、z轴建立空间直角坐标系，所以每个点坐标为P（0，0，2x）；A（2，0，0）；B（2，2，0）；C（0，2，0）；E（1，1，x）；从而可以知道所以E的坐标为（1，1，1）.

（2）设存在F（y，0，z），由E■→F⊥平面PCB得，E■→F·C■→B所以F坐标为（1，0，0）时可使EF⊥平面PCB.

在解决几何问题时，通过直角坐标系向量使问题代数化的同时，不要忽略几何图形本身的定义和性质.

本文以数形结合思想为主体，从两个方面研究了数形结合思想在解题中的应用.在具体的教学中，教师要教授学生具体的用法.本文所涉及的数形结合思想并不全面，还可以更深层次地对复数和立体几何等进行研究，以解决更多的数学问题.

编辑/王一鸣

E-m ail:51213148@qq.com