非均质结构PBX炸药的动态压缩过程模拟

傅 华,李克武,李 涛,刘仓理,彭金华

(1.中国工程物理研究院流体物理研究所冲击波物理与爆轰物理重点实验室，四川 绵阳 621999；2.中国工程物理研究院，四川 绵阳 621999；3.南京理工大学化工学院，江苏 南京 210094)

非均质结构PBX炸药的动态压缩过程模拟

傅 华1,3,李克武1,李 涛1,刘仓理2,彭金华3

(1.中国工程物理研究院流体物理研究所冲击波物理与爆轰物理重点实验室，四川 绵阳 621999；2.中国工程物理研究院，四川 绵阳 621999；3.南京理工大学化工学院，江苏 南京 210094)

采用离散元方法，构建了考虑PBX炸药晶体颗粒与黏结剂非均匀性的计算模型，通过在炸药试样两端采用相向飞片加载、将原SHPB实验的应力边界替代为速度边界的方法，开展了PBX炸药的动态压缩数值模拟研究，再现了考虑PBX炸药非均质特性的SHPB实验过程，获得了不同加-卸载路径下炸药应力应变曲线以及相应的损伤破坏图像。模拟结果表明：在动态压缩过程中，虽然PBX炸药处于整体应力平衡，由于PBX高度非均质性，内部应力分布并不均匀，晶体间应力以应力桥形式传递；应力曲线为试样整体平均，试样内局部所受真实应力可能高于曲线峰值应力；出现卸载回滞曲线的试样发生局部损伤破坏，而完全软化曲线的试样发生整体失稳破坏。

固体力学；动态压缩；离散元方法；PBX炸药；SHPB实验

PBX炸药是战斗部杀伤、破坏和动力能源的关键材料，随着现代高性能武器的飞速发展，对提高PBX炸药在各种条件下安全性的要求日益迫切。武器战斗部装药在勤务过程以及终点弹道阶段，可能经受长脉冲、多次高过载作用、压缩、拉伸、往复压-拉、与壳体壁面的摩擦等复杂过程，PBX炸药力学性能与损伤机理的差异往往导致炸药后续的反应特性与起爆机制的差异，继而对炸药安全性评估产生影响。当前高速侵彻武器装药的安全性评估，除了开展模拟环境条件及综合考核实验，还通过一些基础分解实验获得机理认识和参数参量数据，对影响安全性问题的主控因素进行分析。开展PBX炸药的力学性能与损伤机理研究，可为武器装药的安全性分析提供机理认识与基础数据，是开展炸药安全性研究的重要内容。

近年来，开展了炸药在不同条件下的力学性能与损伤机理研究，主要关注炸药的应力、应变本构关系，考虑应变率和温度的影响，重点关注炸药的动态(中高应变率)力学性能[1-8]，以及力学作用下的损伤模式、损伤与反应特性之间的关系[9-12]等。其中，炸药损伤破坏对其力学性能的影响，特别是PBX炸药在动态压缩过程中表现出的力学性能，与炸药内部损伤演化-破坏变形之间的关联关系，一直是关注的重点。典型PBX炸药是炸药晶体颗粒、黏结剂/钝化剂的混合，炸药表现出的力学性能不仅与内部细观结构密切相关，而且还与炸药多种损伤形式相关。由于力学性能与损伤破坏相互关联的机理相当复杂，难以通过实验直接获得不同载荷阶段对应的损伤破坏状态，目前通常采用数值模拟手段开展相关研究工作。

本文中，采用离散元方法，考虑PBX炸药晶体与黏结剂非均质结构，开展PBX炸药动态压缩过程的数值模拟，获得加-卸载路径下试样应力应变曲线以及相应的损伤破坏图像。

1 数值模拟方法

PBX炸药的Hopkinson压杆实验是常见的动态压缩实验，典型的应力应变曲线如图1所示。曲线一般包含弹性、强化、软化阶段，通过高速摄影可以获得炸药在不同曲线阶段发生的宏观破坏图像，但炸药内部细观响应过程无法获取。采用离散元方法，可模拟应力应变曲线的典型阶段，再现炸药的SHPB动态压缩过程。离散元法(discrete element method,DEM)的基本思想是，把不连续体或连续体离散为具有一定物理意义的独立“微元”或“粒子”，相邻的单元之间存在一种或几种作用力，单元的运动受牛顿第二运动定律支配。它适合于界面弱连接的非连续介质问题或连续体到非连续体转化的断裂、破碎等问题，在开展多组份炸药材料损伤机理模拟研究方面具有算法优势。

计算模型如图2所示，不规则形状代表HMX晶体，其间的填充物为黏结剂，HMX与黏结剂的质量比约为92∶8。HMX平均直径150 μm，离散元单元半径5 μm，黏结剂离散元半径为2 μm，模型总尺寸为1.35 mm×0.67 mm。

图1 典型应力应变曲线Fig.1 Typical stress-strain curve

图2 计算模型Fig.2 Simulation model

采用应力边界需考虑试样两端的入、透射杆长度，这将极大增加计算量。本文中采用飞片在试样两端相向加载的方法，将原SHPB实验的应力边界替代为速度边界，速度分别为v1和v2，为了满足试样的平衡条件，飞片速度满足以下关系式：

式中：t0=2nL/c，L为试样厚度，c为试样的纵波声速，n为声波往返试样内的传播次数，取n=4。

单元间的作用力形式见文献[13]，HMX晶体采用弹脆性模型，黏结剂采用离散元本构方程、朱-王-唐非线性黏弹性模型，其离散元参数见表1。其中，ρ为密度，c0、λ为冲击绝热参数，αij、m、n为中心势作用力参数，μij为摩擦系数，G为剪切模量，Cn为法向黏性系数，εy为屈服应变，εb为法向断裂应变。

表1 材料参数Table 1 Material parameters

2 模拟结果

2.1 弹性阶段

通过人为改变加载脉宽，使试样处于加载-卸载状态，计算可获得应力应变曲线以及对应试样损伤破坏图像。弹性段加-卸载的应力应变曲线以及应力时间曲线如图3所示，试样内部的应力分布与细观结构演化如图4所示。即使试样整体处于应力平衡状态，由于PBX炸药为非均质复合材料，炸药细观结构的应力状态呈现非均匀分布，局部应力有高有低，计算获得试样平均应力峰值约18 MPa(见图4(a))，但炸药局部区域的真实峰值应力却达50 MPa(见图4(b))。

炸药晶体所受应力多大于黏结剂，晶体间的应力以应力桥形式传递，应力局域化现象显著，峰值应力多出现在炸药晶体间的接触处。加载过程，整个试样发生弹性变形阶段，卸载后，试样基本恢复初始状态(见图4(c))。

图3 弹性阶段初期的应力曲线Fig.3 Stress curves at early elastic stage

图4 弹性阶段初期的应力分布与细观结构Fig.4 Stress distribution and meso-structure at early elastic stage

图5 弹性阶段后期的应力曲线Fig.5 Stress curves at later elastic stage

继续加-卸载，应力曲线如图5所示，不同时刻内部应力分布与细观结构如图6所示。试样应力的非均匀分布明显增强，试样内部以应力桥形式传递应力持续增强，局域化现象更显著，侧壁出现局部损伤破坏。90 μs后，应力沿应力桥路径卸载，幅值逐步降低，侧壁的局部损伤破坏加剧，局部颗粒出现分离现象，其余部分承力并发生卸载回滞。

图6 弹性阶段后期的应力分布与细观结构Fig.6 Stress distribution and meso-structure at later elastic stage

2.2 强化阶段

强化阶段加-卸载的应力曲线如图7所示，不同时刻内部应力分布与细观结构如图8所示。试样局部损伤破坏增加，侧壁分离现象加剧；黏结剂所受应力增加，不再承力的损伤破坏区域与继续承力区域边界逐渐明显。在140μs时刻卸载后，应力仍沿应力桥路径卸载，侧壁的分离现象加剧，承力区域呈现出两端大中部小的哑铃状。

图7 强化阶段的应力曲线Fig.7 Stress curves at hardening stage

图8 强化阶段的应力分布与细观结构Fig.8 Stress distribution and meso-structure at hardening stage

2.3 软化阶段

应变软化初期阶段加-卸载的应力曲线、不同时刻内部应力分布与细观结构，如图9～10所示。在140 μs时刻达到曲线应力峰值(56 MPa)后，出现大面积的失稳破坏，未破坏的承力区域逐渐小于损伤破坏区域，未破坏区域的真实应力仍大于峰值应力。在190 μs时刻发生卸载后，损伤破坏现象仍持续加剧，卸载回滞主要由未破坏的承力部分引起。

图9 应变软化阶段初期的应力曲线Fig.9 Stress curves at early strain softening stage

图10 应变软化阶段初期的应力分布与细观结构Fig.10 Stress distribution and meso-structure at early strain softening stage

应变软化后期加载的应力曲线、不同时刻内部应力分布与细观结构，如图11～12所示。伴随着损伤破坏区域的增加，未破坏的真实承力区域越来越少，而计算应力采用面积仍沿用初始面积，导致平均化后试样的应力减小，应变继续增加，形成应变软化阶段。图11中，红色曲线为光滑处理过的应力曲线，蓝色曲线为损伤变量曲线。从图中可知，弹性阶段损伤较小，强化阶段逐渐增大，应力曲线软化阶段达到最大值。

图11 应变软化阶段后期的应力曲线Fig.11 Stress curves at later strain softening stage

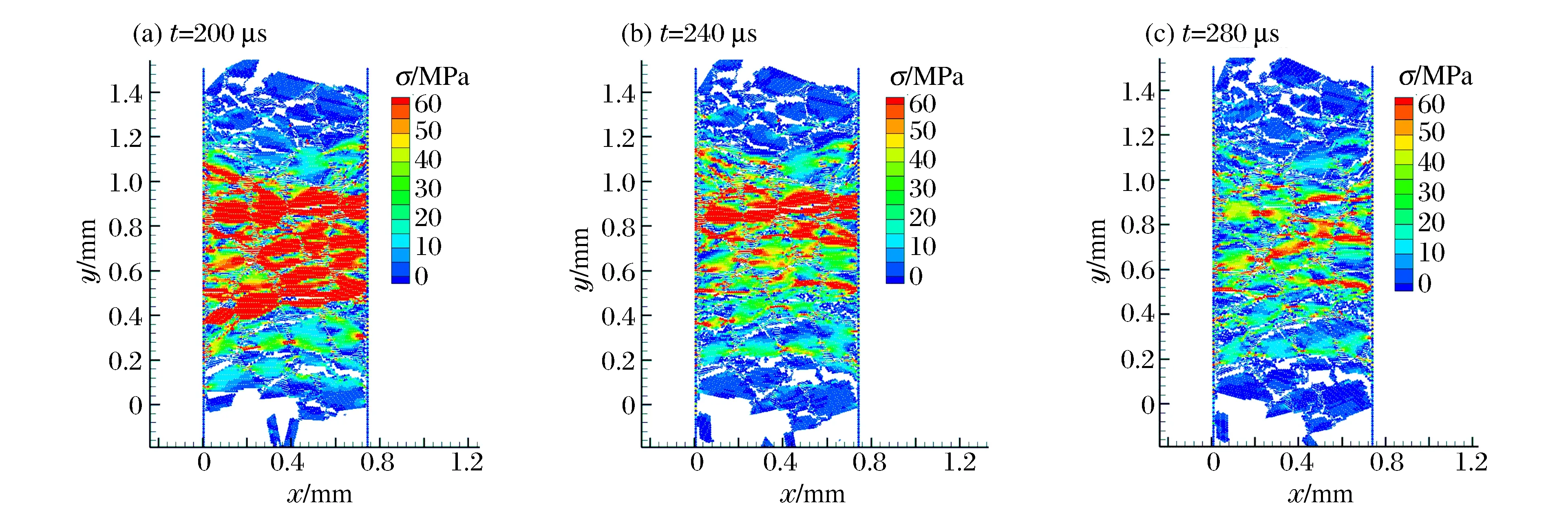
图12 应变软化阶段后期的应力分布与细观结构Fig.12 Stress distribution and meso-structure at later strain softening stage

3 小 结

采用离散元方法，考虑了PBX炸药多组份结构，对炸药应力应变曲线不同阶段进行了细观数值模拟研究，获得了加-卸载路径下试样应力应变曲线以及相应的损伤破坏图像。模拟结果表明：在动态压缩过程中，虽然PBX炸药处于整体应力平衡，由于PBX高度非均质性，内部应力并不均匀，晶体高于黏结剂，应力集中区域出现在晶体接触间，以应力桥形式传递；应力曲线为试样整体平均，即使达到曲线峰值应力后，试样内局部所受真实应力仍可能高于峰值应力；出现卸载回滞曲线的试样发生局部损伤破坏，而完全软化曲线的试样发生整体失稳破坏。

[1] Goudrean G. Evaluation of mechanical properties of PBXW-113 explosive[R]. CA, USA: Lawrence Livermore National Laboratory, 1985.

[2] Hoffman H J. High-strain rate testing of gun propellants[R]. AD-A208826, 1989.

[3] Blumenthal W R. Compressive properties of PBXN-110 and its HTPB-based binder as a function of temperature and strain rate[C]∥12th International Detonation Conference. 2002.

[4] 李英雷,李大红,胡时胜,等.TATB钝感炸药本构关系的实验研究[J].爆炸与冲击,1999,19(4):353-359. Li Yinglei, Li Dahong, Hu Shisheng, et al. An experimental study on constitutive relation of TATB explosive[J]. Explosion and Shock Waves, 1999,19(4):355-359.

[5] 吴会民,卢芳云,卢力,等.三种含能材料力学行为应变率效应的实验研究[J].含能材料,2004,12(4):227-230. Wu Huimin, Lu Fangyun, Lu Li, et al. Experimental studies on strain-rate effects of mechanical behaviors of energetic materials[J]. Energetic Materials, 2004,12(4):227-230.

[6] 傅华,李俊玲,谭多望.PBX炸药本构关系的实验研究[J].爆炸与冲击,2012,32(3):231-236. Fu Hua, Li Junling, Tan Duowang. Experimental study on constitutive relations for plastic-bonded explosives[J]. Explosion and Shock Waves, 2012,32(3):231-236.

[7] 赵玉刚,傅华,李俊玲,等.三种PBX炸药的动态拉伸力学性能[J].含能材料,2011,19(2):194-199. Zhao Yugang, Fu Hua, Li Junling, et al. Dynamic tensile mechanical properties of three types of PBX[J]. Energetic Materials, 2011,19(2):194-199.

[8] Skidmore C B, Phillips D S, Howe P M. The evolution of microstructural changes in pressed HMX explosives[C]∥Short J M, Kennedy J E. Paper Summaries-Eleventh International Detonation Symposium. Snowmass, 1998:268-272.

[9] Rae P J, Goldrein H T, Palmer S J P. Studies of the failure mechanisms of polymer-bonded explosives by high resolution moire interferometryand environmental scanning electron microscopy[C]∥Paper Summaries-Eleventh International Detonation Symposium. Snowmass, 1998:235-239.

[10] Demol G, Lambert P, Trumel H. A study of the microstructure of pressed TATB and its evolution after several kinds of insults[C]∥Paper Summaries-Eleventh International Detonation Symposium. Snowmass, 1998:404-406.

[11] 傅华,李俊玲,谭多望.PBX炸药动态Brazilian试验及数值模拟研究[J].高压物理学报,2012,26(2):148-154. Fu Hua, Li Junling, Tan Duowang. Dynamic Brazilian test and simulation of plastic-bonded explosives[J]. Chinese Journal of High Pressure Physics, 2012,26(2):148-154.

[12] 李俊玲,傅华,谭多望,等.PBX炸药的拉伸断裂损伤分析[J].爆炸与冲击,2011,31(6):624-629. Li Junling, Fu Hua, Tan duowang, et al. Fracture damage analysis of PBX[J]. Explosion and Shock Waves, 2011,31(6):624-629.

[13] 傅华,刘仓理,王文强,等.细观尺度下塑料粘结炸药热点生成的初步模拟研究[J].爆炸与冲击,2008,28(6):515-520. Fu Hua, Liu Cangli, Wang Wenqiang, et al. Preliminary simulation of hot spot formation for plastic bonded explosives at mesoscale[J]. Explosion and Shock Waves, 2008,28(6):515-520.

(责任编辑 丁 峰)

Simulation of dynamic compression of plastic-bonded explosives considering heterogeneous structure

Fu Hua1,3, Li Kewu1, Li Tao1, Liu Cangli2, Peng Jinhua3

(1.NationalKeyLaboratoryofShockWaveandDetonationPhysics,InstituteofFluidPhysics,ChinaAcademyofEngineeringPhysics,Mianyang621999,Sichuan,China;2.ChinaAcademyofEngineeringPhysics,Mianyang621999,Sichuan,China;3.DepartmentofChemistry,NanjingUniversityofScienceandTechnology,Nanjing210094,Jiangsu,China)

The plastic-bonded explosives (PBX) simulation model with heterogeneous crystal grain and binder was presented using the discrete element method(DEM). By loading opposite flyers at both ends of the explosive sample, the dynamic compression simulation was performed adopting velocity as the boundary condition instead of stress as the boundary condition in the Hopkinson test, and replicated the compression process in the Hopkinson test. The stress-strain curves and their corresponding damage fracture images under different loading-unloading paths in the explosive sample were captured. Our simulation results indicated that the stress distribution in PBX is not uniform and the stress propagates in the form of stress bridges between crystals due to the heterogeneous structure. The actual stress in PBX can be higher than that shown by the curve's peak stress. The samples on the unloading hysteresis curves reveal local damage, while those on the completely softening curves indicate fractures resulting from integral instability.

solid mechanics; dynamic compression; discrete element method; plastic-bonded explosives; SHPB experiment

10.11883/1001-1455(2016)01-0017-07

2014-06-27； < class="emphasis_bold">修回日期：2014-09-10

2014-09-10

国家自然科学基金项目(11272294,11272296);中国工程物理研究院科学技术发展重点基金项目 (2012A0201007);冲击波物理与爆轰物理重点实验室专项项目(2012-专-05)

傅 华(1979— )，男，博士研究生，副研究员,huafu-103@163.com。

O347.3 <国标学科代码：1301540 class="emphasis_bold"> 国标学科代码：1301540 文献标志码：A国标学科代码：1301540

A