集对分析在区域大气环境风险评价中的应用研究
邢永健,王 旭,杜 航 (沈阳航空航天大学安全工程学院,辽宁 沈阳 110136)
集对分析在区域大气环境风险评价中的应用研究
邢永健,王 旭*,杜 航 (沈阳航空航天大学安全工程学院,辽宁 沈阳 110136)
摘要:应用集对分析法对事故状态下有毒有害气体环境风险分布建立数学模型,通过南京化工园区的实例分析,把评价区域大气环境风险划分为5个等级,并对差异不确定系数i取值进行讨论,以反映不同状态下的大气环境风险分布水平.研究结果显示,i1=0.5,i2=-0.5取值方法简便,且此时的区域大气环境风险状态相对符合实际,可为优化土地利用规划和完善环境风险防控措施提供依据.
关键词:集对分析法;区域大气风险;风险叠加;差异不确定系数i
* 责任作者, 教授, wangx1960@126.com
近年来,随着城镇化和工业化的快速推进,人口、基础设施和工业企业的高度集中以及产城融合的发展所带来的环境风险问题日益突出,工业企业突发性事故(火灾、爆炸和泄露等)频发,释放的有毒有害物质通过大气传播,对人身健康、自然生态以及社会经济带来严重威胁.
合理的风险防控措施,如优化产业布局[1-3]、风险分级管理[3-7]等,可有效降低环境风险,而大气环境风险评价是其决策的基础依据.Roy等[8]研究应用事故树分析法计算四氯化钛泄漏事故发生概率,并釆用情景分析法进行事故后果的评价;通过对不同有毒化学物质的泄漏扩散进行模拟,Bubbico等[9]指出化学物质的沸点是影响扩散距离的主要因素;Buckley等[10]对某次氯泄漏事故进行模拟,研究了氯气在大气中的传输和沉积过程;为解决气体泄漏事故中存在的不确定性问题,孙燕君等[11]研究采用蒙特卡洛分析法对氯气泄漏事故中的变量进行分析,并通过仿真模拟,得到模拟结果及其概率分布;李跃宇等[7]考虑可信最严重事故场景下,环境风险源在现有风险管理水平和当地可预期气象条件下的事故影响概率和健康危害,以获得健康风险并划分风险源等级;刘毅等[12]综合运用风险识别技术、CALPUFF大气扩散模型、空间分析方法,构建了石化园区规划层面大气环境风险模拟方法.
总之,多数大气环境风险评价方法的基本思路是,采用CALPUFF、SLAB等模型对风险源在最不利或各种气象条件下发生的最大可信事故的后果进行模拟分析,计算出事故状态下有毒有害气体的浓度分布,并按各污染物的风险基准,确定出污染物相应的影响范围,进一步确定该范围内的风险受体情况,并采用风险防控措施.但在大尺度空间,以上研究未能有效描述多风险源释放产生多重压力的风险叠加.信息扩散法[13-14]为风险叠加提供了思路,但在解决区域大气环境风险评价中因多风险源、多途径和多风险受体所带来的空间信息不足和不确定问题依然困难.因此,本文应用集对分析法,并结合信息扩散法的思想来探讨区域大气环境风险评价方法.该方法把空间信息的不确定性转化为数学问题进行定量计算,通过对差异不确定系数取值进行讨论,可反映不同风险状态下的空间信息,在一定程度上消除了风险评价的主观性和片面性,为优化土地利用规划和完善环境风险防控措施提供更为科学的基础依据.
1 集对分析
1.1 基本原理
集对分析(Set Pair Analysis)(又称联系数学)是从系统的角度去认识确定性和不确定性的关系,并认为研究对象是一个确定不确定的系统.它可以统一描述和处理随机性、模糊性、不完整性等不确定性因素引起的确定不确定系统[15].假设给定集合A和B,组成集对H=(A,B),其联系度可通过式(1)进行数学表达.

式中:µ为联系度,值域为[-1,1];a、b、c分别为同一度、差异度、对立度,且a+b+c=1;i为差异标记符号或相应系数,取值区间为[-1,1];j为对立标记符号或相应系数,且j≡-1.
1.2 模型构建
用集对分析进行不确定性分析需要客观承认不确定性,不确定性与确定性作为一个系统进行分析和处理[15].有毒有害气体环境风险分布存在确定与不确定的因素,如有毒有害气体传播的载体大气是确定的,但大气在事故发生时如何流动是不确定的.而且确定与不确定的演变是一个连续的、动态的过程,由于时空的变化,大气环境风险分布在不断改变,也是一个动态的过程.
对有毒有害气体环境风险分布可按梯形模糊关系进行简化计算[13-14],同时,薛鹏丽等[16]依据高斯模型构建的大气环境风险场指数旨在从污染气象条件角度反映大气环境风险场的空间差异,从环境风险场角度反映区域突发环境风险的相对特征.这为构建基于集对分析的大气环境风险分布计算模型提供了依据.将集对分析用于区域大气环境风险评价,就是将区域某单元与风险源所在单元的距离集合A和评价标准集合B一起构成一个集对H.通过集合A中每项数值与集合B中的评价标准范围进行比较,集对H的联系度可通过式(2)表示.再通过一系列转化(见2.2 节),以评价区域大气环境风险水平的高低.

式中:µ为联系度;l为计算点与风险源点的距离;i、j分别为差异系数、对立系数;s1、s2、s3、s4为评价标准,区间(0,s1]、(s1,s2]、(s2,s3]、(s3,s4]、(s4,+∞)分别为高度、中度、中低度、低度、无影响区(在考虑风险因子实际浓度时,s可根据风险源释放的风险因子物化性质作出调整).
2 案例分析
南京化工园区位于长江北岸,是国家级南京江北新区的重要组成部分,目前规划面积45km2,实际开发面积29.2km2.园区以石油化工和合成材料、精细化工等石油深加工企业为主,且园区内及外围分布若干居民区、生态保护区等环境保护目标敏感区域,一旦发生突发性环境事故,极易造成重大环境损害.
区域网格化是解决大尺度空间信息多样性和复杂性的有效手段.把南京化工园区及周边的二维空间用500m等步长划分为相同大小的正方形区域单元,然后用一个62行65列的矩阵来表示该二维空间,用正方形中心点的信息量来代表单元,此时矩阵内各单元的值为0.
2.1 风险源识别
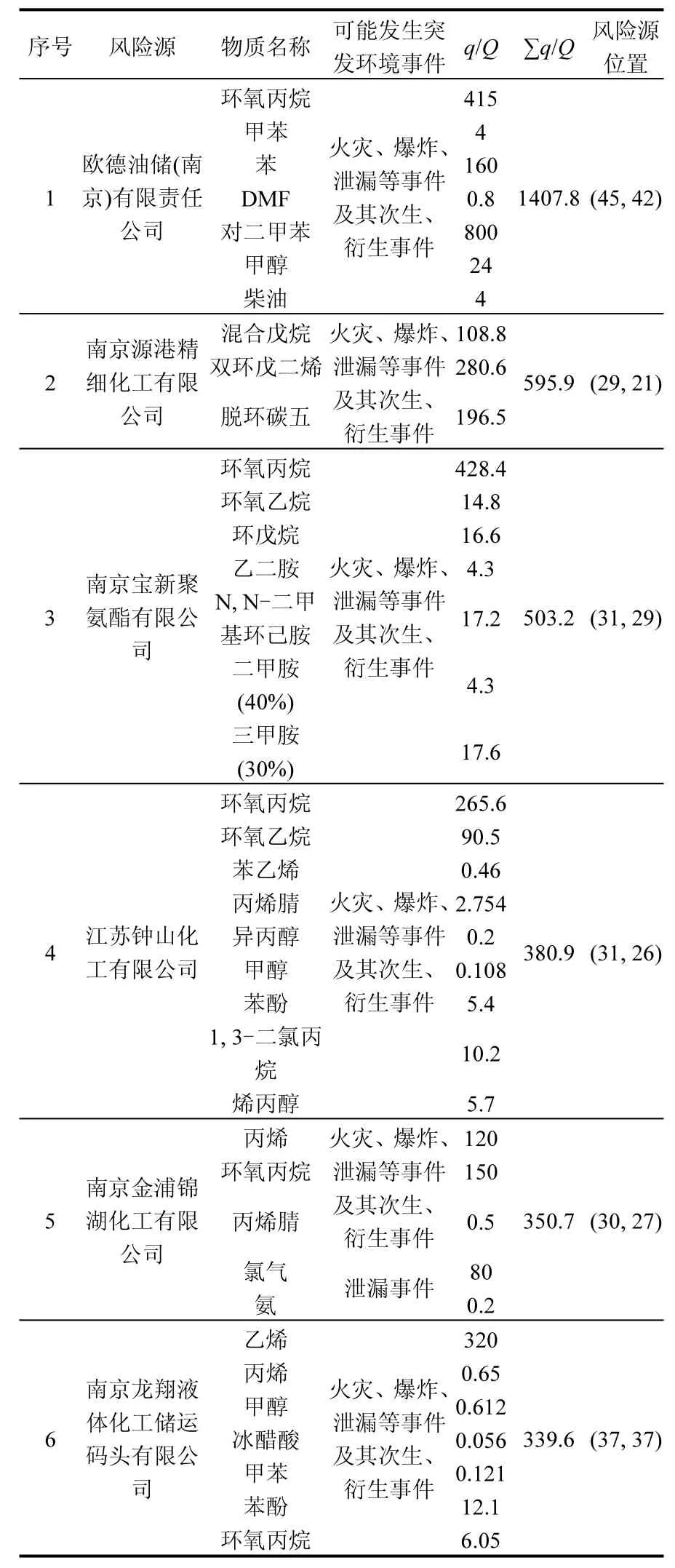
表1 南京化工园区部分企业环境风险源信息Table 1 Environmental risk sources information of partial enterprises in Nanjing Chemical Industry Park
因研究区域范围较大,所以把一家企业作为一个环境风险源单元处理,并确定其在矩阵中的位置.在一般大气条件下为气态的有毒有害物质是风险源识别的重点,但液体、固态的危险化学物质,在发生火灾、爆炸、泄漏等事件时极易引发次生、衍生大气污染事故,也需重点识别.不同的风险物质有不同的理化性质,对环境风险受体的作用机制和损害程度也不同,这是风险叠加的难点.应用归一化的思想,把不同物质的风险量度同一化,由式(3)得到区域内环境风险源指数Q.

式中:qi为每种危险化学品实际存在量,t;Qi为与各危险化学品相对应的临界量,t.
根据系统安全优先次序,筛选出风险源指数最大的前25家企业作为评价对象.因篇幅有限, 表1是其中6家企业的环境风险源信息.
2.2 风险值计算
为使联系度µ具有物理意义,同时基于文献[16]中式(4)构建风险计算模型的思想,可通过式(4)表达计算点单一风险因子的暴露水平.

原国家环保总局发布的《建设项目环境风险评价技术导则》(HJ/T 169-2004)[17]规定大气环境影响一级评价范围距离源点不低于5km,二级评价范围距离源点不低于3km,在其后续修订征求意见稿中规定三级评价距建设项目边界不低于1km.基于此,式(2)中评价标准s1、s2、s3分别取1000、3000、5000m,考虑到超过5km后,有毒有害气体仍会对人身健康和生态环境造成影响,故s4取10000m.2.1节求得的各环境风险源指数Q为归一化后无纲量值,故对于不同风险源,评价标准s不用调整.
风险值如何计算更具科学性,目前还没有定论.《建设项目环境风险评价技术导则》(HJ/T 169-2004)[17]给出了环境风险值为事故发生概率与事故造成的环境(或健康)后果的乘积的计算方法.类似的,区域某风险源释放的风险因子扩散到某单元的风险指数可表示为:
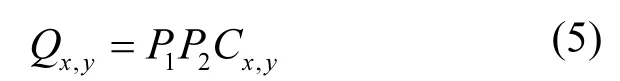
式中:Qx,y为计算点单一风险因子释放的风险指数;P1为风险因子释放概率,可通过历史数据统计得到,取10-5/a;P2为风险因子转运到计算点的概率,等于区域年平均风频,见表2;Cx,y为计算点单一风险因子的暴露水平.

表2 南京化工园区近20年年均风频统计表Table 2 The average of annual wind frequency in Nanjing Chemical Industry Park in past 20 years
由式(3)(4)(5)计算区域各单元大气环境风险指数,然后对各单元若干风险指数进行求和叠加.最后由式(6)得小数形式的风险值,并通过去余取整的方法对大气环境风险进行分级,分级依据见表3.


表3 区域大气环境风险水平划分Table 3 Classification of levels of regional atmospheric environmental risks
2.3 对i取值的讨论
a、b、c是宏观层次上确定不确定性的表征,而差异系数i是对微观层次上的不确定性的表征.不确定性的本质是不确定,因此,i的值很难确定,而且具有多值性,需要根据不同的情况作不同的分析[18].风险源(企业)的风险管理水平、空间的气象条件(风速、风向、大气稳定度)和地形等因素影响大气环境风险水平,那么这些因素在微观层次可通过集对分析数学化,即i是这些因素的数学表达.i在-1和1之间变化,体现了确定性与不确定性之间的相互转化,i取-1与1,都是确定性的,随着i趋近0,不确定性明显增加[19].当风险源(企业)的风险管理水平降低、空间的气象条件和地形有利于有毒有害气体传播,那么i值将向1靠近;随着风险源(企业)的风险管理水平、空间的气象条件和地形有利于有毒有害气体传播向不利于面变化,i值将经过0,直至趋近于-1.
i的取值方法有顺势取值法、逆势取值法、计算取值法、随机取值法、特殊值法[15].在此,对i采用特殊取值,通过讨论i取值可了解区域大气环境风险程度.
当i1=i2=1时,差异度转化为同一度,表达的现实意义是距风险源近的区域大气环境风险与源单元的风险具有一致性,区域大气环境风险分布见图1(a).此时,评价区域一半以上处于极高和高风险状态,占评价区域的51.99%,其中极高风险区域占评价区域的20.74%.对于高风险区域在风险管理水平和气象条件不同的情况下,有可能转变为极高风险区域,也有可能转变为中风险区域.应对处于极高和高风险区域的环境风险受体进行识别、管理,合理布局产业区、居民区等功能区,从根本上改善区域大气环境风险水平.
当i1=i2=-1时,差异度转化为对立度,大气环境极高和高风险区域明显减少[图1(b)],占评价区域的7.99%.这表明气象条件不利于有毒有害气体的传播、区域风险管理处于最优水平、大气环境风险处于最低状态.若区域风险管理水平下降,尤其是各企业的风险管理水平下降,区域大气环境风险将会上升.因此,应继续加强风险管理,保持区域大气环境风险处于最低状态.
以上取值均属于极端情况,为得到比较实际的区域大气环境风险状态,通常采用中间值,取i1=0.5,i2=-0.5,得到的区域大气环境风险分布见图1(c).与图1(a)相比,极高风险区域明显减少,只占评价区域的6.15%.这表明,通过提高区域环境风险管理水平,可有效降低区域大气环境风险水平.与图1(c)相比,得到的信息是区域大气风险形势不容乐观.但如果考虑效益问题,实现i1=i2=-1时的低风险水平成本很高,是不可接受的.因此,i1=0.5,i2=-0.5时的区域大气环境风险状态相对符合实际.
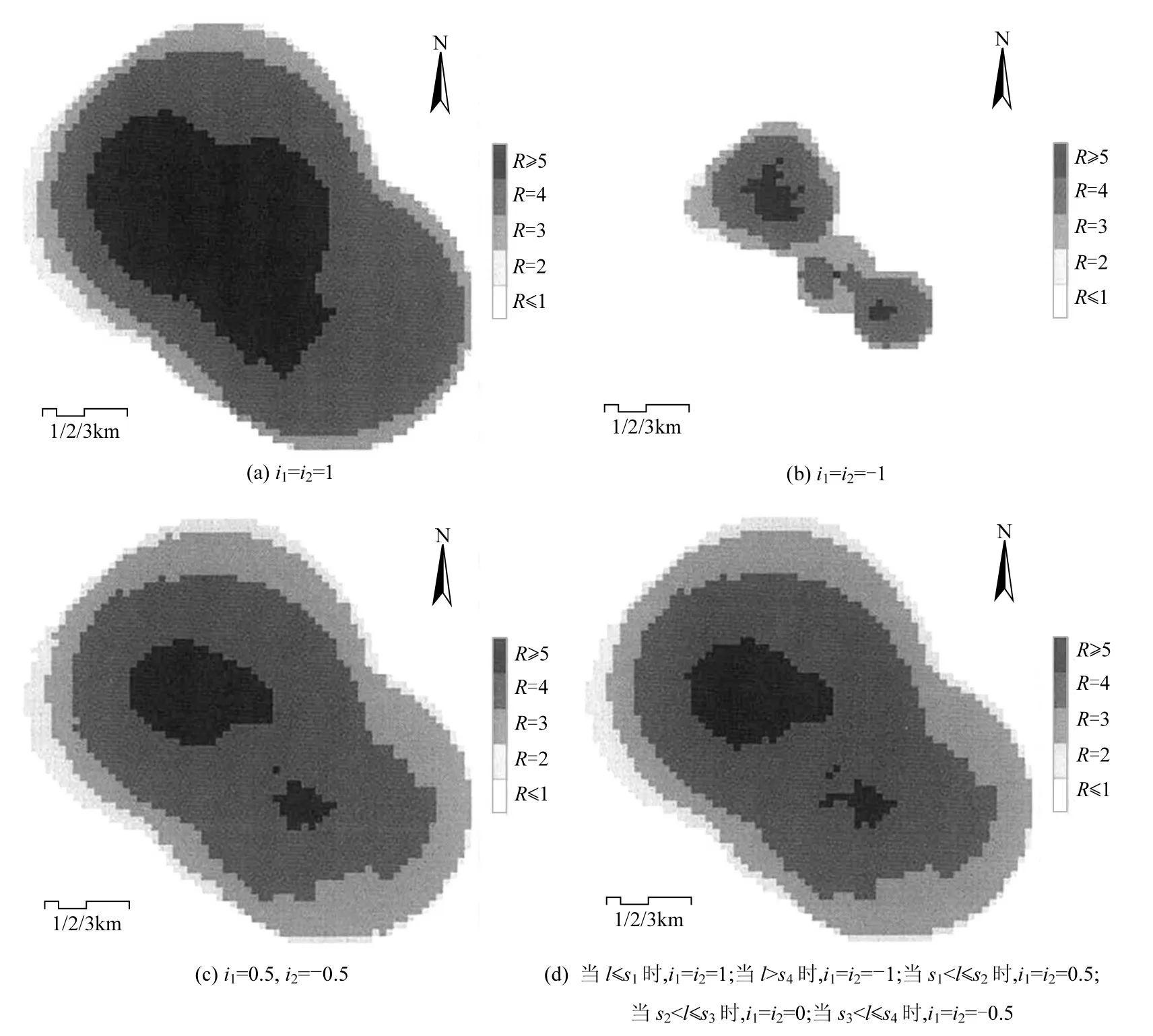
图1 区域大气环境风险Fig.1 Regional atmospheric environmental risk 当l≤s1时,i1=i2=1;当l>s4时,i1=i2=-1;当s1 文献[19]给出了与灰色聚类分析中白化函数的确定方法基本相同的i值确定方法.属于某级别,判为同一,是确定性的,i=1;远离该级别,判为对立,也认为其是确定性的,i=-1;在级别区间附近,较难判断,故认为其存在差异性,在对立与同一之间转化,越接近某级别,i值越接近1,越接近相隔的评价级别,i值越接近-1[19].基于此,并参考特殊值法(i取0.5,0或-0.5),当l≤s1时,i1=i2=1; 当l>s4时,i1=i2=-1;当s1 2.4 结果分析 图1(c)中,大气环境风险极高区域分布在风险源周围,且向主导风向下风向偏移趋势明显.统计得评价区域各行政区所涉及的大气环境风险值,继而计算各行政区大气环境风险均值(四舍五入),见表3.极高、高风险区域可能出现有毒有害气体造成的灾难性后果(人员死亡),或者危害公众的身体健康.所以相关行政区的风险极高区域严禁存在居民区,并预先做好企业员工的应急疏散措施,同时制定本行政区的突发环境事件应急预案.政府部门可依据图1(c)和表3进行环境风险分级管理,优化土地利用规划,完善环境风险防控措施. 表3 南京化工园区及周边行政区的环境风险值Table3 Environmental risk values for districts of Nanjing Chemical Industry Park and the surrounding 多风险源、多途径和多风险受体所带来的空间信息不足和不确定性是区域大气环境风险评价的难点,不确定性主要体现在风险源释放风险因子的时间、分布不确定等方面. 1)在这里,时间的不确定性应用概率表示.由于缺乏信息来源,25个风险源释放风险因子的概率都为10-5/a,而风险源释放风险因子的时间与企业风险管理有较大关联,因此,需要合理评估各企业的风险管理水平以确定其风险源释放风险因子的概率. 2)分布的不确定性通过调节i的取值进行处理(如2.3节所述),并联合区域年平均风频表示.本文是对25个风险源统一进行i的取值,而且取值粗糙,为得到更加精确的结果,在今后的研究中需探讨不同风险源i取值的问题. 3)本文分析了风险源(企业)的风险管理水平、空间的气象条件和地形等因素影响i大小、正负变动的趋势,但如何将这种趋势定量化还需深入研究. 4)在通过集对分析将大气环境风险于空间分布的描述过程中,评价标准s在宏观层次影响着分布的不确定性.本文求得的各环境风险源指数Q为归一化后无纲量值,故对于不同风险源,s未予调整,这使得风险叠加结果存在偏差.在考虑风险因子实际浓度时,s可根据风险源释放的风险因子物化性质作出调整. 5)需要说明的是,i的取值影响到b是倾向于同一性还是对立性,始于风险源的大气环境风险状态怎样分布与i值有关.也就是说,i的取值可影响风险源释放风险因子的时间、分布等不确定性的处理.i取何值、其取值方法的科学性是今后研究的方向. 4.1 应用集对分析理论,对事故状态下有毒有害气体环境风险分布建立数学模型,能有效解决空间信息不足、不确定的问题,将不确定性转化为数学问题进行定量计算,计算过程简单,获取数据方便. 4.2 对差异系数i取值的讨论,系统的描述所论集对的同一性、差异性和对立性联系,反映了不同风险状态下的空间信息,便于多方面对比讨论,在一定程度上消除了风险评价的主观性和片面性. 4.3 通过对南京化工园区的实例分析,当i1=0.5,i2=-0.5时,得到区域大气环境风险与园区现状有较好的一致性,可为优化土地利用规划和完善环境风险防控措施提供基础依据. 参考文献: [1] 谢元博,李 巍,郝芳华.基于区域环境风险评价的产业布局规划优化研究 [J]. 中国环境科学, 2013,33(3):560-568. [2] Zhou Y F, Liu M. Risk Assessment of Major Hazards and its Application in Urban Planning: A Case Study [J]. Risk Analysis, 2012,32(3):566-577. [3] 夏 秋,钱 瑜,刘萌斐.基于环境风险评价的危险品道路运输优化选线—以张家港市为例 [J]. 中国环境科学, 2014,34(1):266-272. [4] 贾 倩,黄 蕾,袁增伟,等.石化企业突发环境风险评价与分级方法研究 [J]. 环境科学学报, 2010,30(7):1510-1517. [5] Giubilato E, Zabeo A, Critto A, et al. A risk-based methodology for ranking environmental chemical stressors at the regional scale [J]. Environment International, 2014,65:41-53. [6] Pizzol L, Critto A, Agostini P, et al. Regional risk assessment for contaminated sites Part 2: Ranking of potentially contaminated sites [J]. Environment International, 2011,37(8):1307-1320. [7] 李跃宇,卢 彬,宋永会,等.基于公众健康的大气环境风险源定量分级方法 [J]. 环境科学研究, 2012,25(1):83-88. [8] Roy P K, Bhatt A, Rajagopal C. Quantitative risk assessment for accidental release of titanium tetrachloride in a titanium sponge production plant [J]. Journal of Hazardous Materials, 2003, 102(2/3):167-186. [9] Bubbico R, Mazzarotta B. Accidental release of toxic chemicals: Influence of the main input parameters on consequence calculation [J]. Journal of Hazardous Materials, 2003,151(2/3): 394-406. [10] Buckley R L, Hunter C H, Werth D W, et al. A case study of chlorine transport and fate following a large accidental release [J]. Atmospheric Environment, 2012,62:184-198. [11] 孙燕君,钱 瑜,张玉超.蒙特卡洛分析在氯气泄漏事故环境风险评价中的应用研究 [J]. 环境科学学报, 2001,31(11):2570-2577. [12] 刘 毅,刘 龙,李王锋,等.石化园区规划大气环境风险模拟方法与案例 [J]. 清华大学学报(自然科学版), 2015,55(1):80-86. [13] 刘桂友,徐琳瑜.一种区域环境风险评价方法——信息扩散法[J]. 环境科学学报, 2007,27(9):1549-1556. [14] Xu L, Liu G. The study of a method of regional environmental risk assessment [J]. Journal of Environmental Management, 2009, 90(11):3290-3296. [15] 赵克勤.集对分析及初步应用 [M]. 杭州:浙江科学技术出版社, 2000. [16] 薛鹏丽,曾维华.上海市突发环境污染事故风险区划 [J]. 中国环境科学, 2011,31(10):1743-1750. [17] HJ/T 169-2004 建设项目环境风险评价技术导则 [S]. [18] 朱 兵,王文圣,王红芳,等.集对分析中差异不确定系数i的探讨[J]. 四川大学学报(工程科学版), 2008,40(1):5-9. [19] 沈珍瑶,张 征,谢彤芳.集对分析在环境质量评价中应用的探讨 [J]. 环境保护, 1999,(10):20-21. Set pair analysis for regional atmospheric environmental risk assessment. XING Yong-jian, WANG Xu*, DU Hang (School of Safety Engineering, Shenyang Aerospace University, Shenyang 110136, China). China Environmental Science, 2016,36(2):634~640 Abstract:Because multiple sources release multiple stressors and these stressors affect multiple habitats and endpoints, the spatial information of interaction is limited and uncertain. Set pair analysis (SPA) can effectively describe and deal with the environmental risk systems with limited and uncertain spatial information and model the distribution of environmental risk of poisonous gases after accidents. In this paper, the regional atmospheric environmental risk of Nanjing Chemical Industry Park was analysed by SPA model. In order to describe the distribution of atmospheric environmental risks in different conditions, this paper classified the risks into 5 levels and discussed the value of variation uncertainty coefficient. Under i1=0.5, i2=-0.5, the analysis is not complex and the level of regional atmospheric environment risks is close to the actual situation. The analysis result under these variation uncertainty coefficient can guide the optimization of land use planning and improvement of environmental risk control measures. Key words:set pair analysis;regional atmospheric risk;risk superposition;variation uncertainty coefficient i 作者简介:邢永健(1989-),男,江苏徐州人,沈阳航空航天大学安全工程学院硕士研究生,主要从事系统安全理论与应用、环境风险评价与管理研究. 收稿日期:2015-07-27 中图分类号:X820.4 文献标识码:A 文章编号:1000-6923(2016)02-0634-07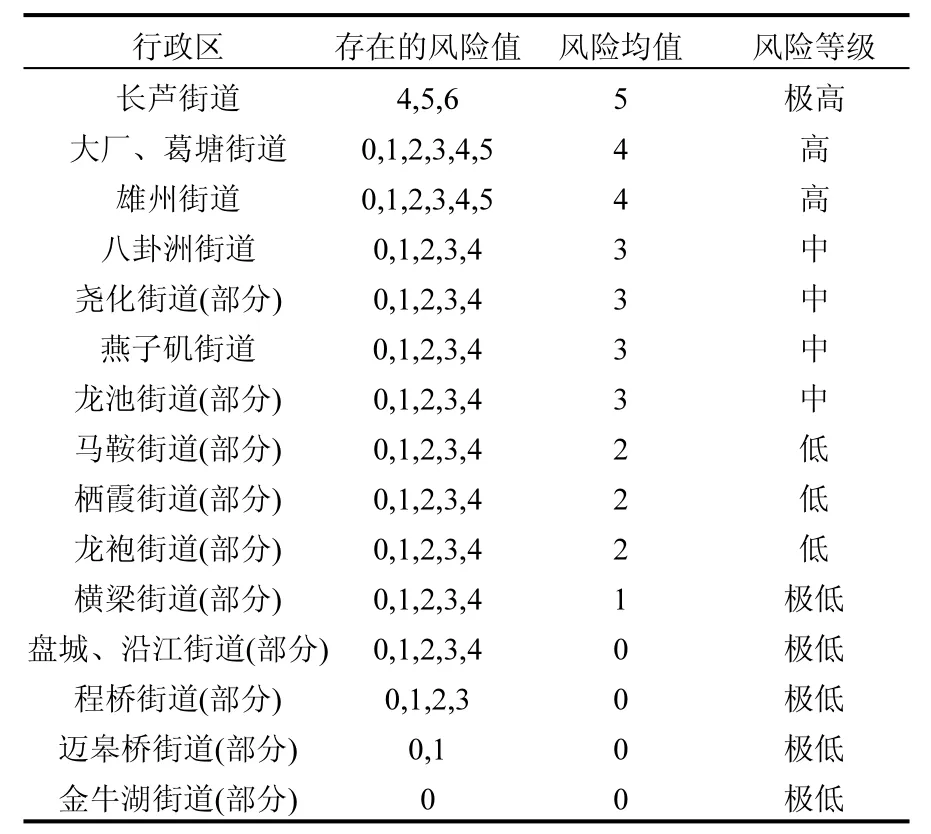
3 讨论
4 结论

