基于位置域频率和相位辨识的永磁直线电机推力波动抑制技术研究*
张彦龙,赵 飞,张 驰,杜文华
(1.中北大学 机械与动力工程学院,太原 030051;2.中国科学院宁波工业技术研究院(筹) 先进制造技术研究所,浙江 宁波 315201)
基于位置域频率和相位辨识的永磁直线电机推力波动抑制技术研究*
张彦龙1,赵飞2,张驰2,杜文华1
(1.中北大学 机械与动力工程学院,太原030051;2.中国科学院宁波工业技术研究院(筹) 先进制造技术研究所,浙江 宁波315201)
摘要:推力波动是永磁直线电机固有的内部扰动,严重影响直线电机的动态精度。基于推力波动特性辨识结果设计前馈控制器是实现推力波动抑制的重要手段。首先分析了推力波动特性,基于位置域频率和初相位信息建立了推力波动数学模型。电机在不同速度下运行时基于遗传算法辨识方法分别确定实验直线电机的推力波动模型参数,并设计前馈控制器,实现直线电机的推力波动抑制。仿真和实验结果表明,推力波动模型准确描述了被测电机的推力特性,基于模型辨识结果设计的前馈控制器有效地降低了推力波动引起的系统速度波动。
关键词:永磁同步直线电机;前馈补偿;推力波动;遗传算法
0引言
永磁同步直线电机是进给系统实现高加速度高精度运动的关键基础部件。直线电机简化了进给系统的传动链,消除了传动间隙,减少了摩擦,提高了运行速度和加速度,扩展了控制带宽范围,促进了高速高精密加工的发展。然而,直驱电机并非完美无缺,直线电机端部磁场的畸变影响到行波磁场的完整性,使电机损耗增加,推力减小,而且存在较大的推力波动。直线电机由于不需要中间机械转换环节,使得其较旋转电机更容易受到外界干扰。推力波动是影响直线电机性能的主要因素之一。引起推力波动的原因有齿槽效应、端部效应、法向吸引力所引起的摩擦摄动以及驱动电流的非正弦和反电动势的非正弦所引起的纹波推力等因素[1-4]。推力波动会使电机在运行时出现抖动、噪声并且影响电机运行的平稳性,因此为了提高直线电机的驱动性能,必须对推力波动进行抑制。
针对直线电机的推力波动可以从电机设计角度和控制角度来进行抑制。电机的设计角度可以通过将齿槽结构优化、对动子铁心结构优化和对磁极结构优化实现一定程度的抑制[5-6]。通过优化电机设计的方法,可以降低永磁同步直驱电机的推力波动。然而,电机设计并不能完全消除推力波动,需通过控制来弥补。在控制角度,利用现代控制技术,提高系统扰动抑制能力是实现推力波动的主要趋势。文献[7-9]通过迭代学习的方法对推力波动进行补偿,但该方法增加了系统的复杂度和运算量,使得实时控制系统的使用成本大幅增高。文献[10] 基于扰动观测器的推力波动补偿控制需要额外的系统资源,同样造成成本提升。文献[11]通过外部电机拖动实验直线电机匀速运动的方式测得了推力波动中的齿槽力和端部力,并对其进行了补偿,但该方法需要额外的电机、力传感器,且不能测出推力波动中的纹波力。为了同时获得齿槽力、端部力、纹波力和法向吸引力所引起的摩擦摄动,本文通过驱动器使电机匀速运行,通过测量输出电流获取电机的推力波动。首先分析了推力波动特性,基于位置频率和初相位信息建立了推力波动数学模型。在多组运动速度状态下,基于遗传算法辨识方法分别辨识出直线电机推力波动的模型参数,以此设计前馈控制器,实现直线电机的推力波动抑制。
1推力波动的建模及补偿方法
1.1推力波动的建模
在id=0矢量控制方式下,电机的推力电流和电机的推力成正比。当电机运行时,其受力情况可表示为式(1)、式(2):
F=ma+Ffriction+Fripple
(1)
F=Kiq
(2)
其中:F为电机电磁推力;m为动子质量;a为电机的加速度;Ffriction为摩擦力;Fripple为推力波动;K为电机力常数;iq为经过坐标变换后电机的q轴电流。
永磁直线电机的推力波动主要由齿槽力、端部力以及纹波力等引起。从理论上对它们进行理论推导后发现,这些影响因素都可以表示成同电机初级所处的位置和电机的运行速度有关正弦函数组合的形式。故在某一速度下的推力波动模型可设为:
(3)
其中,l为正整数;Ai为第i次谐波的幅值;fi为第i次谐波的频率;x为电机初级所处的位置;φi为第i次谐波的初相位。不同速度时,推力波动模型中的幅值和相位略有差别。
由式(3)可知,推力波动是关于电机运动位移的函数,同电机运行的时间并非直接相关。若电机匀速运行,则很容易建立起电机运行的位移和时间的关系。这种情况下,电机的受力情况为:
F=Ffriction+Fripple
(4)
建模时应首先确定其正弦函数的频率,快速傅里叶变换是一种简单而有效的求取信号特征频率的方法。电机匀速运行时易于建立起电机运行的位移和时间的关系,因此可以求出以位置为变量的特征频率,此时频率的单位是mm-1。
1.2基于遗传算法的模型参数的辨识
为了获得推力波动具体的数学表达式,需要对模型中的参数Ai和φi进行参数辨识。遗传算法由于具有较强的全局搜索能力,当需要辨识的参数较多时,不易陷入局部最优解。故本文采用遗传算法辨识模型参数。取待辨识的推力波动参数向量为个体,遗传算法的每步迭代得到推力波动参数的辨识值为:
(5)
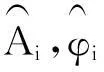
则由下式得到相应的推力波动辨识值:
(6)
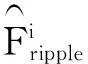
遗传算法的目标函数和个体适应度分别取为:
(7)
fm=Cmax-J
(8)

1.3推力波动前馈控制补偿

图1 系统结构框图
当控制系统误差具有可预测性时,前馈控制是实现误差消减的直接而有效的方法。直驱电机的推力波动具有位置周期特性,因此,可以采用基于参考模型前馈控制的方式进行抑制。由于各频率分量所对应的幅值和相位随着速度变化而变化,需对多个速度情况下的推力波动模型进行上述运算,辨识出每一速度下的模型参数,计算出各频率下的幅值和相位同速度的关系式,即Ai=Ai(v)和Φi=Φi(v),带入式(3)得到推力波动模型。通过指令速度即可算得此速度下的Ai和Φi,进而求得对应的推力波动。以此设计的前馈控制器系统框图如图1所示。
2永磁同步直线电机推力波动补偿及仿真
本文在Matlab/Simulink环境中建立速度闭环和电流闭环控制系统,仿真对象为永磁同步直线电机,其参数如表1 所示。根据上述分析结果,推力波动可以表示为一系列正弦函数的组合。假设电机在速度为300mm/s情况下运行,推力波动最大值为电机连续推力的4.81%。按照式(3),直线电机推力波动模型参数如式(9)所示。在Simulink环境下,构建直线电机速度环和电流环控制模型,并将论文提出的前馈控制方法加入到系统中,如图1所示,前馈控制器模型参数通过论文1.2节辨识方法进行辨识,辨识结果分别为A1=165.9113、A2=288.189、Φ1=1.3949和Φ2=2.305。仿真结果如图2所示。当系统无前馈控制时,系统推力波动范围为近1000N,当系统加入前馈后,推力波动几乎为0。由于输出电流受噪声影响和参数辨识误差的存在,使得系统推力波动并不能完全被抑制。从仿真结果可以看出,补偿后的推力波动范围和稳态速度波动较补偿前被明显抑制,验证了电流环加入补偿电流以抑制推力波动的可行性。

表1 电机参数
Fripple=166sin(2π*0.05x+1.4)+
288sin(2π*0.1x+2.3)
(9)

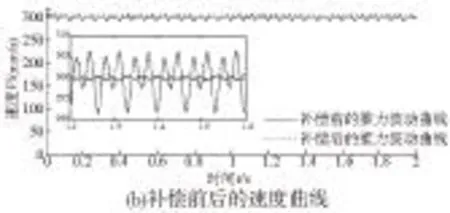
图2 补偿前后的推力波动曲线和稳态速度曲线
3永磁直线电机推力波动补偿实验及结果讨论
3.1实验配置

图3 实验配置
论文所提出的方法被应用于一台永磁同步直线电机实验台上。该实验台直线电机采用7极6槽结构,其它相关参数如表1所示。位置传感器采用发格LS487光栅尺。试验台控制器采用dSPACE1103控制仿真系统搭建,驱动器采用Copley Xenus型驱动器。整个永磁同步直驱电机伺服系统平台如图3所示。
3.2伺服电机推力测试及分析技术

图4 推力波动信号的频谱
本文采用的id=0的矢量控制方式中,由于伺服电机运行时的推力和推力电流成正比,故测出电机输出电流值即可得电机推力值。调节Copley驱动器使电流闭环,通过Copley对电机的输出电流进行采样并记录,而电机输出电流信号中的直流分量为电机所受的摩擦力。例如当控制器闭环并且使电机工作在20mm/s时,将去除直流分量后的电流信号乘以电机电磁力常数得到推力波动信号如图5a所示。对该信号按位置进行FFT分析,得到其频率特性,如图4所示,由此可确定推力波动数学表达式如式(10)所示。
(10)
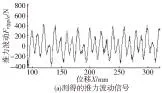
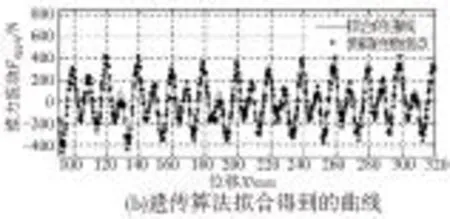
图5 实验测得的推力波动曲线和遗传算法拟合的曲线
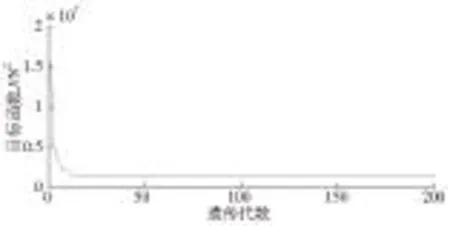
图6 目标函数J的优化过程
通过遗传算法即可辨识出模型中的Ai,Φi,其拟合曲线和目标函数J的优化过程分别如图5b和图6所示。由上面的分析可知,不同速度下,相同频率分量所对应的幅值和初相位并非相同,需在多种不同速度下进行推力波动参数辨识。本文共进行102次实验测量,同一速度进行3次重复实验。最后经计算得到各频率下的幅值和相位同速度的关系式。结果显示,3次重复试验所获得的幅值和相位基本重合。同一速度值下的相位随运动方向不同略有差别。这是由于随着速度的增加,iq和反电动势增加,而输入的电流往往并非理想的正弦电流,导致电磁推力中存在高次谐波,进而影响到推力波动的初相位。
3.3结果讨论
在MATLAB/simulink中搭建电机的速度闭环控制器,并将其加载到dSPACE1103中,将推力波动转换成对应的电流值加入到电流环控制器中,以对推力波动进行抑制。当电机运行在300mm/s时,其补偿前后的推力波动曲线和速度曲线如图7所示。
从图7a可以看到,在没有推力波动补偿情况下,直线电机运行时受推力波动的影响比较大,加入推力波动补偿后推力波动被明显抑制。由图7b可知,没加入推力波动前馈补偿时电机运行的速度波动范围为3.733%。对直线电机进行推力波动补偿后,其运行的速度波动范围为1.633%。从实验结果可以看出,补偿后速度的波动较未补偿降低55%以上,推力波动的影响得到了明显削弱,可见本文提出的辨识方法是可行的。应当指出的是,电机在运行时受噪声影响,使得推力的波动并不能完全被抑制。同时,电磁推力常数随着位置变化也会略有不同,导致电磁推力和q轴电流并非呈严格的正比关系,使得辨识出的推力波动数学模型存在误差。论文的下一步工作为将电磁推力常数的变化也加入推力波动的辨识中并降低电机运行时的噪声影响,使得补偿效果更好。


图7 补偿前后的推力波动曲线和稳态速度波形
4结论
针对推力波动对直驱伺服系统的影响,本文建立了基于推力波动数学模型的前馈补偿策略。首先将测得的推力波动信号通过FFT提取信号中的特征频率,然后采用遗传算法推力波动辨识出推力波动模型中的参数,最后根据推力波动模型设计前馈控制器。通过在一台永磁同步直驱电机的实验研究表明,该方法明显抑制了直线电机稳态速度波动。同时该方法实现过程较为简单,不需要额外的实验设备和传感器,前馈补偿器不复杂且运算量小,实时性强。
[参考文献]

[2]Kim I, Nakazawa N, Kim S, et al. Compensation of torque ripple in high performance BLDC motor drives[J]. Control Engineering Practice, 2010, 18(10): 1166-1172.
[3]夏加宽, 沈丽, 彭兵, 等. 齿槽效应对永磁直线伺服电机法向力波动的影响[J]. 中国电机工程学报, 2015,35(11):2847-2853.
[4]Liu C T, Hwang C C, Li P L, et al. Design Optimization of a Double-Sided Hybrid Excited Linear Flux Switching PM Motor With Low Force Ripple[J].IEEE Transactions on Magnetics, 2014,50(11):1-4.
[5]王光辉, 陈杰, 蔡涛, 等. 多目标分解随机粒子群优化算法及其在直线电机优化设计中的应用[J].控制理论与应用,2013,30(6):693-701.
[6]Gebregergis A, Chowdhury M H, Islam M S, et al. Modeling of Permanent-Magnet Synchronous Machine Including Torque Ripple Effects[J]. IEEE Transactions on Industry Applications, 2015,51(1):232-239.
[7]Zhao S, Tan K K. Adaptive feedforward compensation of force ripples in linear motors[J]. Control Engineering Practice, 2005, 13(9): 1081-1092.
[8]王福忠, 张利敏. 基于迭代算法的 PMLSM 推力波动抑制策略[J]. 计算机仿真, 2014, 31(5): 276-278.
[9]Kalaivani L, Subburaj P, Iruthayarajan M W. Speed control of switched reluctance motor with torque ripple reduction using non-dominated sorting genetic algorithm (NSGA-II)[J]. International Journal of Electrical Power & Energy Systems, 2013, 53: 69-77.
[10]甄文喜, 戴跃洪, 唐传胜,等. 永磁同步直线电机伺服系统负载扰动建模与抑制[J]. 组合机床与自动化加工技术, 2013(2):7-10.
[11]林家春, 李伟, 赵彤, 等. 永磁直线同步电动机推力波动抑制策略[J]. 控制理论与应用, 2007,24(3):449-452.
(编辑李秀敏)
Research of Force Ripple Compensation for Permanent Magnet Synchronous Linear Motor Based on Frequency and Phase Identification
ZHANG Yan-long1,ZHAO Fei2,ZHANG Chi2,DU Wen-hua1
(1.School of Mechanical and Power Engineering, North University, Taiyuan 030051, China;2. Institute of Advanced Manufacturing Technology, Ningbo Institute of Industrial Technology CAS, Ningbo Zhejiang 315201, China)
Abstract:The thrust fluctuation which affects the dynamic precision of the linear motor seriously is inherent and internal disturbance in permanent magnet synchronous linear motor. The feedforward controller designed according to the results of thrust fluctuation characteristic identification is an important means to realize the force ripple suppression. This paper firstly analyze the characteristics of the force ripple and build the mathematic model of the trust fluxtuaion based on the position frequency and initial phase information. Model parameters are identified through genetic algorithm method, The feedforward controller is designed to achieve the suppression of the force ripple. Simulation and experimental results show that the force ripple model accurately describes the characteristics of the tested linear motor. And the designed feedforward controller based on model identification results effectively reduce the velocity fluctuation.
Key words:permanent magnet synchronous linear motor; feedforward compensation; force ripple; genetic algorithm
中图分类号:TH39;TG506
文献标识码:A
作者简介:张彦龙(1990—),男,黑龙江齐齐哈尔人,中北大学硕士研究生,研究方向为电机控制, (E-mail)zhangyanlong@nimte.ac.cn;通讯作者:张弛(1978—),男,河南扶沟县人,中科院宁波工业技术研究院先进制造所研究员,博士,研究方向为精密运动控制技术,(E-mail)zhangchi@nimte.ac.cn。
*基金项目:国家自然科学基金项目(51207158);国家自然科学基金项目(51405479);中国博士后科学基金资助项目(2015T80639);宁波市创新团队(2012B82005);宁波市重大专项(奥马特)(2013B10042&2013B10043);中科院百人计划(2015A610146,2015A610154)
收稿日期:2015-09-25
文章编号:1001-2265(2016)03-0086-04
DOI:10.13462/j.cnki.mmtamt.2016.03.024

