基于随机概率的并联机构运动可靠性分析*
吴任和,张 策
(1.广东轻工职业技术学院 机械工程学院,广州 510300;2.天津大学 机械工程学院,天津 300072)
基于随机概率的并联机构运动可靠性分析*
吴任和1,张策2
(1.广东轻工职业技术学院 机械工程学院,广州510300;2.天津大学 机械工程学院,天津300072)
摘要:针对3UPS-PU并联机构进行运动学分析。运用齐次坐标变换理论推导出其运动学逆解方程。在此基础上,对其进行微分变换得到位姿输出误差正解模型。然后应用随机概率模拟该机构在不确定因素下,观测其位姿输出误差的变化情况。基于数理统计和机构的许用精度范围求解该机构的运动可靠度。结果表明,该机构在正常工作的条件下能够运行可靠、平稳。
关键词:并联机构; 运动学;随机概率;运动可靠性
0引言
运动可靠性是评价并联机构性能的一项重要指标,主要是考核机构在不可控因素下机构精度的变化情况。目前,国内外大多数学者考虑并联机构加工制造和装配存在的公差,驱动构件重复位置精度误差以及外部因素的存在随机性的研究还比较少。夏吉兵,杨强[1-2]等人考虑原始输入误差的随机性,对机构系统进行了运动可靠性分析;张义民,Choi D H[3-4]等人针对不同的平面机构,在假定设计变量和设计参数服从正态分布的前提下,建立了机构的运动精度可靠性分析模型,并对部分设计参数分布概率未知情况下的机构运动精度可靠性稳健设计问题进行了初步探索;孙志礼,杨强[5]等利用ADAMS软件对3-RPS并联机构的运动可靠性进行了分析并计算得到该机构的运动可靠性。
本文针对3-UPS-PU并联机构进行运动可靠性研究。在对该机构的运动学位置逆解求解的基础上,对其进行微分变换得到位姿输出误差正解模型。然后应用随机概率统计求解机构的运动可靠性。
1并联机构的结构描述
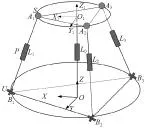
图1 3-UPS/PU并联机构结构简图
3-UPS-PU并联机构主要由定平台、动平台、三条结构完全相同的驱动支链和一条恰约束支链组成。对于其中任意一条驱动支链来说,其一端以虎克铰(U副)与定平台连接,另一端以球副(S副)与动平台连接,中间为移动副(P副)。对于中间的恰约束支链,其底端与定平台固定,顶端以虎克铰与动平台连接,中间为移动副。其结构简图如图1所示。
2机构的运动学求解
2.1坐标系的建立

2.2位置逆解分析
采用RPY组合变换表示动平台运动姿态。其旋转次序为:
RPY(φ,θ,ψ)=Rot(Z1,φ)Rot(Y1,θ)Rot(X1,ψ)
(1)
该机构没有绕Z轴转动的自由度,因此φ=0。则旋转变换矩阵R可进一步表示为:

(2)
则Ai在定坐标系中的坐标OAi可表示为:
OAi=R·Ai+O1
(3)
则其位置逆解为:
Li=OAi-Bi=(R·Ai+O1)-Bi
(4)
根据(4)式即可得到三条驱动支链li的位置逆解的函数式。
3误差正解模型的建立
在考虑3-UPS-PU并联机构的杆长误差、球铰铰点安装误差和虎克铰安装误差的情况下,运用微分法求解其末端执行器的位姿输出误差[6-7]。
令li表示动支链的杆长,ni表示由Bi指向Ai的单位向量。则3-UPS/PU并联机构的位置逆解方程可表示为:
li·ni=OAi-Bi=(R·Ai+O1)-Bi
(5)
对(5)式左右两端进行微分处理,可得:
dli·ni+li·dni=dR·Ai+dAi·R+dO1-dBi
(6)
(7)
为了建立3-UPS/PU并联机构位姿误差输出正解模型,现将(7)式进行简化处理。
由并联机构的微分关系可得:
dni=Δni·ni
(8)
式中:
(9)
所以:
(10)

(11)
式中δRy,δRx表示坐标变换矩阵R分别对θ,ψ求微分。
上式可写成:
(12)
令δli=dli,δAi=dAi,δBi=dBi,则(12)式可写为:
(13)
将(13)式进一步整理为:
δl=JX·δD+JP·δm
(14)
式中,
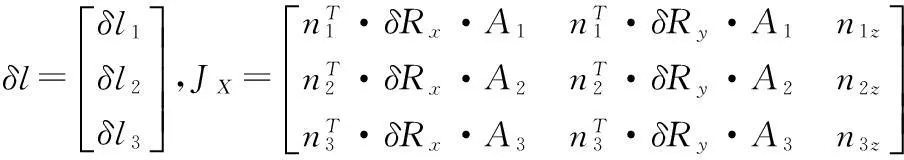
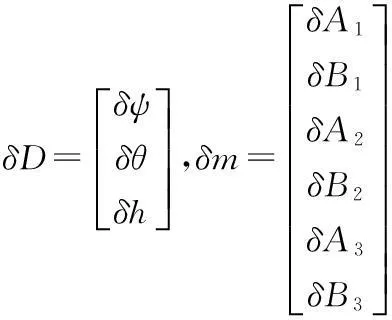
由此可得到3-UPS/PU并联机构位姿误差输出正解模型:
(15)
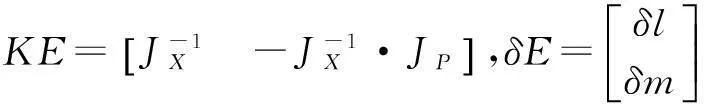
则(15)式可写为:
δD=KE·δE
(16)
在3-UPS-PU并联机构位姿误差输出正解模型(16)式中,δD∈R3×1为动平台末端执行器的位姿输出误差,KE∈R3×21为考虑该机构的杆长误差、球铰铰点安装误差和虎克铰铰点安装误差的误差传递系数矩阵,δE∈R21×1为该机构的杆长误差、铰点安装误差参数向量[8-9]。
4机构运动可靠性分析
4.1机构运动可靠性定义及评价指标
机构的运动可靠性是指机构在规定的使用条件下,在规定的使用期内,精确、及时、协调的完成规定机械运动的能力,用概率来度量时,即为机构运动可靠度R。可靠度R是机构运动可靠性的最常用的评价指标[10-11]。
设机构的输出参数为Y(t),是随机变量,机构输出参数的允许值范围为[Y下,Y上],当Y下 R=P(Y下 (17) 对应的机构失效概率Pf为: Pf=1-R=1-P(Y下 (18) 4.2实例分析 本文在构造3-UPS-PU并联机构铰点安装误差数据与杆长误差数据的基础上,结合求解其位姿输出误差的理论模型,运用随机概率统计法来研究在大批量生产该机构时其末端执行器在三个位姿方向的可靠度。 给定该机构的结构参数为:动平台半径ra=300mm、定平台半径rb=500mm和初始高度h=1200mm。设定并联机构的铰点安装误差与杆长误差均服从正态分布。为了便于分析,假设铰点安装误差与杆长误差的均值与方差如表1与表2所示。 表1 批量生产的并联机构误差抽样均值 表2 批量生产的并联机构误差抽样方差 根据给定的误差均值与方差,由概率统计构造30000组符合正态分布的误差数据作为该机构的误差样本。然后根据该机构位姿输出误差理论求解出机构的位姿输出误差,对其进行统计,进而获得输出误差的均值与方差。 图2 动平台X轴转角误差样本分布图 图3 动平台Y轴转角误差样本分布图 图4 动平台Z轴位置误差样本分布图 根据由蒙特卡洛法求解得到的3-UPS-PU并联机构末端执行器在三个输出方向的位姿误差数据进行统计计算,求解各个方向产生的误差的均值与方差如表3所示。 表3 位姿输出误差均值与方差 机构的运动可靠性与许用输出精度也有关系,当许用输出精度的范围较大时,其可靠性较高,而当许用输出精度的范围较小时,其可靠性也会相应的降低。在此以给定该机构X方向与Y轴方向的许用输出精度为[-0.0003rad,0.0003rad]以及给定Z轴方向的许用精度范围为[-0.06mm,0.06mm],来求解机构在各方向的运动可靠性。 将表3中各方向输出误差的均值、误差与给定的在其相应方向的许用输出精度代入公式并查标准正态分布表得: (1)X方向的运动可靠性为: (2)Y方向的运动可靠性为: (3)Z方向的运动可靠性为: 5结束语 本文主要对3-UPS-PU并联机构的运动可靠性进行了研究,主要完成了以下几方面工作: (1)应用坐标变换法建立了3-UPS-PU并联机构的运动学位置逆解; (2)在位置逆解的基础上,运用微分变换法,对3-UPS-PU并联机构的位姿输出误差正解模型进行了求解; (3)根据求解的位姿输出误差正解模型,利用随机概率统计建立了运动可靠性的求解方法,并对该机构的运动可靠性进行了分析。 [参考文献] [1] 夏吉兵,汪永超,赵建平. 基于可拓学理论的数控机床可靠性评价研究[J]. 组合机床与自动化加工技术,2015(3):157-160. [2] 杨强,孙志礼,闫明,等. 改进Delta 并联机构运动可靠性分析[J]. 航空学报,2008,29(3):487-491. [3] Choid H,Yooh H. Reliability analysis of a robot manipulator operation employing single Monte-Carlo simulation[J]. Key Engineering Materials, 2006,321-323(Pt2):1568-1571. [4] 张义民,黄贤振,贺向东.不完全概率信息牛头刨床机构运动精度可靠性稳健设计[J]. 机械工程学报,2009,45(4):105-110. [5] 孙志礼,杨强,闫明,等,3-RPS并联机器人运动可靠性仿真研究[J].机械科学与技术,2007,26(6):780-786. [6] 高猛,李铁民,郑浩峻,等. 并联机床铰链制造误差的补偿[J]. 清华大学学报(自然科学版),2003,43(5):617-620. [7] 王晓磊. 3-SPS+SP并联机构误差建模及灵敏度分析[J].组合机床与自动化加工技术,2014(12):105-108. [8] Brien J F O,Wen J T. Redundant actuation for improving kinematic manipulability.IEEE International Conference on Robotics and Automation(ICRA),1999,2:1520-1525. [9] Stewart D. A Platform with Six Degrees of Freedom [J]. Proceeding of the Institute for Mechanical Engineering, 1965, 180(15): 371-386. [10] Karouia M, Hervé J M. Asymmetrical 3-dof Spherical Parallel Mechanisms. European Journal of Mechanics A-Solids, 2005(24): 47-57. [11] 苏玉鑫,段宝岩.六自由度 Stewart 平台运动精度分析[J].西安电子科技大学学报(自然科学版),2000,27(4):401-403. (编辑李秀敏) Kinematic Reliability Analysis of Parallel Mechanism Based on Random Probability WU Ren-he1,ZHANG Ce2 (1.School of Mechanical Engineering,Guangdong Industry Technical College, Guangzhou 510300, China;2.School of Mechanical Engineering, Tianjin University, Tianjin 300072,China) Abstract:The kinematics of the 3-UPS-PU parallel mechanism was analyzed and the inverse kinematics solution was derived adopting the homogeneous coordinate transformation theory. The output pose error model was obtained with differential transformation based on previous work. Then the change of the posture error on output was observed under random factors. The mechanism motion reliability was solved in terms of the mathematical statistics and the allowable range accuracy. The results show that the mechanism can work reliably and stably under normal working conditions. Key words:parallel mechanism; kinematics; random probability; kinematic reliability 中图分类号:TH112;TG659 文献标识码:A 作者简介:吴任和(1978—),男,广东增城人,广东轻工职业技术学院讲师,硕士,研究方向为微纳制造、CAD/CAE,(E-mail)wurenhe520@126.com。 *基金项目:广东省自然科学基金项目(S2013010011882) 收稿日期:2015-05-10;修回日期:2015-06-05 文章编号:1001-2265(2016)03-0041-03 DOI:10.13462/j.cnki.mmtamt.2016.03.011