齿轮成形磨削淬硬温度场与组织场仿真研究*
王 杰,洪荣晶,张 金,方成刚
(1.南京工业大学 机械与动力工程学院,南京 211816;2.南京工大数控科技有限公司,南京 211816)
齿轮成形磨削淬硬温度场与组织场仿真研究*
王杰1,洪荣晶1,张金2,方成刚1
(1.南京工业大学 机械与动力工程学院,南京211816;2.南京工大数控科技有限公司,南京211816)
摘要:为了真实反映成形磨削淬硬过程中温度、组织分布状态,基于热力学和相变动力学数学模型,根据ABAQUS用户子程序接口DFLUX、USDFLD,按照FORTRAN语法规则编写代码对CAE软件进行二次开发,模拟分析了成形磨削淬硬包括冷却全过程的温度场及组织转变过程,预测工件在不同方向的温度变化及磨削淬硬完成后马氏体组织分布情况,计算工件淬硬层深度,评定其淬透性。结果表明,距表层0.32mm以上的材料将激活相变,淬硬层深度约为0.291mm。仿真模拟对磨削淬硬中控制马氏体转变量具有一定的指导作用。
关键词:成形磨削淬硬;ABAQUS二次开发;温度场;相变效应
0引言
随着现代制造业和科学技术的不断进步,工业生产对机械零件的加工精度、表面质量、寿命以及对其生产率提出了更高的要求。零件通常在热处理后,采用磨削作为最终加工工艺。相比其它机械加工方式,磨削加工切除单位体积材料需要更多的能量输入,这些能量转化为磨削热并集中于工件表层,机械行为与切削热共同作用可能导致已淬硬材料出现热损伤。德国学者考虑将热处理与磨削工序集成起来,提出了磨削淬硬技术,利用磨削热对工件进行表面淬火的新型复合技术。既提高效率,合理利用磨削热,又避免工件热损伤。磨削淬硬技术有着极大的经济与社会效益,国内外学者对其进行了研究。国外的Nguyen和Zhang[1]对外圆磨削淬硬数值模拟,结果表明进给量对淬硬层深度起决定作用。马占龙,韩正铜[2]运用有限元分析软件ANSYS建立磨削淬硬温度场,对淬硬层深度进行预测,并由试验验证仿真可靠性。袁威,刘菊东[3]结合试验与仿真,研究磨削用量对单程磨削淬硬层深度的影响,试验与仿真结果一致,表明淬硬层深度与磨削深度成正比,与工件进给速度成反比。
成形法加工齿轮精度、效率高,而由于接触线长,冷却状况差,磨削热量输出高,对表层组织温度场、组织场影响很大。应用传统的实验方法因受制于现有的实验手段,对诸如工件表层马氏体分布,热等参数的研究结果并不尽如人意,因此本文采用仿真的方法来研究成形磨削淬硬温度场、组织场。
1成形磨削力计算模型
磨削力来自于砂轮磨粒与工件接触后产生的弹塑性变形及系统内部相互摩擦作用。磨削力表征磨削过程,是磨削淬硬过程中能量消耗、热量产生及磨削振动的重要原因,是影响材料去除机制、砂轮磨损以及加工表面质量基本条件[4]。砂轮与齿面的接触面就像磨削平面时被弯曲,所以成形磨齿可以认为是一种倾斜曲面磨削。根据C.Guo的倾斜面磨削理论[5],可以把成形磨齿接触面等效为普通平面磨削进行研究,等效模型如图1所示。
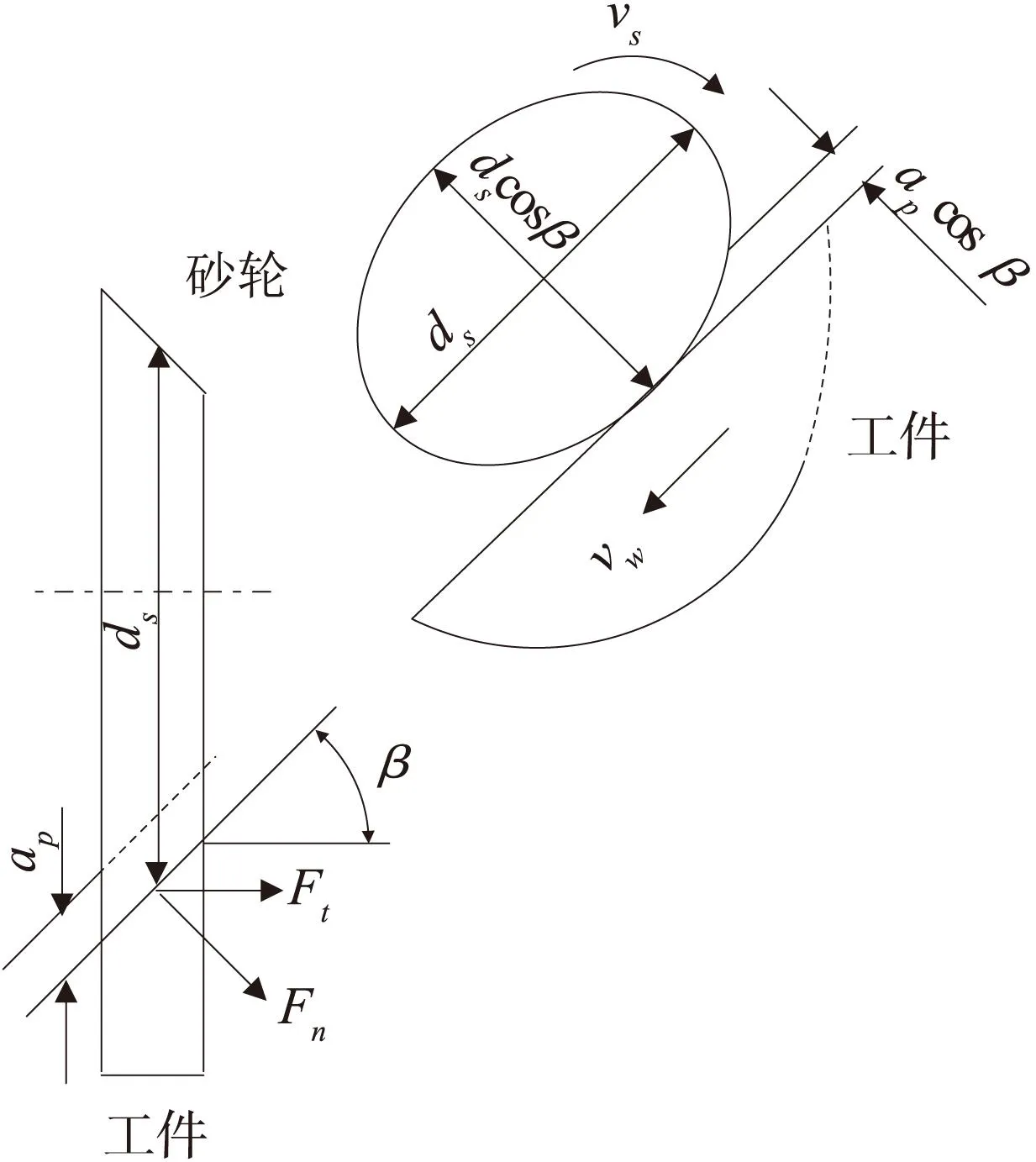
图1 成形法磨齿等效模型
如图1所示,砂轮径向磨削深度为ap,被磨齿轮压力角为α,在过砂轮宽度b上任意点磨削区上的几何情况可以通过过该点的沿α余角方向的投影截面来讨论。直径为ds的圆形砂轮形状投影到和砂轮回转平面成α余角的、与被磨齿面相垂直的平面上后,砂轮形状为椭圆形,其长轴为ds,短轴为dssinα。
同理可以计算出其余等效参数,等效后的砂轮转速vs,进给速度vw及接触线长度lc不变,数值改变的参数如表1所示。

表1 平面磨削与成形磨削参数间关系
根据陈勇平平面磨削计算模型[6],最终得到成形磨齿计算模型:
(1)
2磨削淬硬温度场及相变理论
2.1温度场理论模型
(1)热流密度模型
工件材料磨削淬硬过程消耗大量的功,这些能量几乎全部转化为热,用热流密度q表示。磨削弧区产生的总热流密度可以通过切向磨削力计算得到:
(2)
式中:Ft为成形磨削切向力,vs为砂轮转速,lc为磨削接触线长度,b为磨削区接触宽度。
(2)热量分配比模型
在温度场仿真中,一个关键的参数就是热量分配比,即磨削消耗的功转化为热被传递到工件的那部分。Rowe[7]在深入研究工件与砂轮磨粒相互作用基础上,总结了干磨下的热量分配比计算模型:
(3)

2.2相变理论
(1)扩散型转变
扩散型转变与温度、时间有关,相变起始时间即孕育期,转变开始到结束即长大过程[8]。奥氏体转变,珠光体、贝氏体转变皆属于扩散型转变。对于扩散型转变数学模型,Johnson、Avrami等人[9-10]作了大量工作,相变量可由下式求得:
V=1-exp(1-btn)
(4)
式(4)称为Avrami方程,其中V为转变量,t为等温时间,n和b为变量,与温度相关,是通过转变量为10%和90%的两组方程来确定。
Avrami方程描述的是等温下转变过程,对于磨削淬硬这种连续冷却过程不能直接使用。需要将时间离散,将每一小段时间看成等温转变,并叠加计算孕育率和转变量[11]。
(2)非扩散型转变
不同于扩散型转变,非扩散型转变的相变量仅取决于温度,与时间无关。国外学者Koistinen和Marbulge[12]研究提出非扩散型相变动力学模型:
(5)
式中:V为马氏体组织转变量;Ms为马氏体点,可由经验公式求得,这里参考清华大学聂振国论文[13]结论,42CrMo的马氏体点取326℃,α取0.01931;T为绝对温度。
3磨削淬硬有限元仿真
磨削淬硬数值模拟需要复杂有限元模型数据输入,包括几何模型,热物性材料特性参数,初始条件,边界条件和加载条件等。有限元模型主要特征的简要描述如下。
3.1网格划分

图2 网格划分
网格密度通常取决于作用载荷和边界条件。磨削淬硬过程中,磨削区及其附近伴随着高热流输入和高温度梯度,因此,对工件表层1mm进行网格细划分以保证计算精度及收敛性。而模型下部采用比例网格划分技术划分较粗网格,以提高计算效率。针对磨削淬硬温度场仿真,网格划分采用8节点隐式线性热传导单元DC3D8,网格划分如图2所示。
3.2工件材料和磨削参数
42CrMo强度、淬透性高,韧性好,广泛应用于齿轮、汽车连杆等制造。磨削淬硬有限元模拟需要输入材料热物性参数。42CrMo的热物性参数如表2所示。
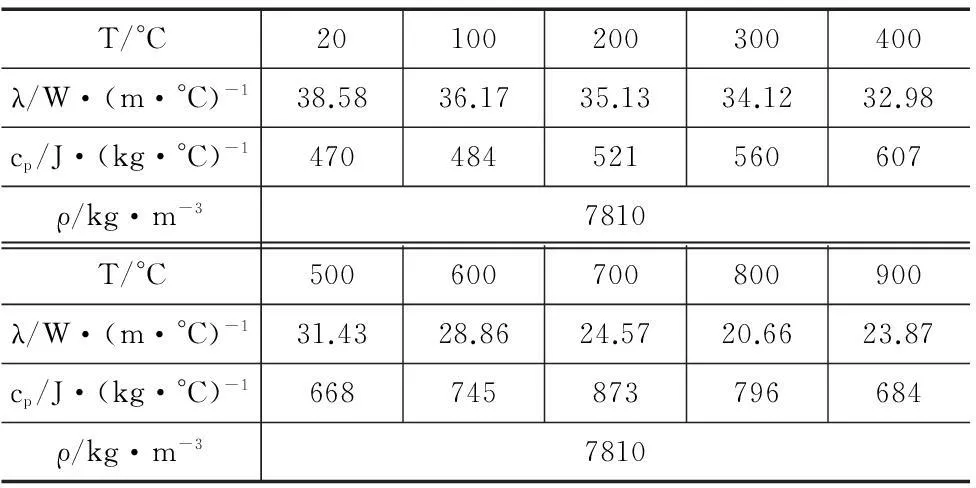
表2 42CrMo热物性参数
磨削淬硬过程是一种高度的非线性过程,工件的热导率、比热既是温度的函数,同时又随着相体积分数的变化而变化。因此,伴随着不同组织间的转变,它们的热物性存在差异,需要采用混合定律,并在ABAQUS中调用场变量实现。
(6)
(7)
式中:x表示某一参数变量,如热导率、比热等,Xi表示某一组织的相应参数值,i分别代表奥氏体、马氏体等组织相,δi表示某一组织体积分数。
磨削淬硬仿真模拟其它必要磨削参数如下表所示。其中,表3为砂轮物理特性表,砂轮材料为棕刚玉,外径D为400mm。表4为成形磨齿工艺参数表。

表3 砂轮物理特性

表4 成形磨齿工艺参数
3.3初始和边界条件
环境温度可视为工件初始温度,取T(t=0)=25℃。在磨削淬硬过程中,工件外表面与外界始终存在对流换热,通常由牛顿冷却公式[14]求得:
(8)
式中:hconv为对流换热系数,q为热流密度,T-T0为温差。
3.4热源加载
成形磨削淬硬过程极其复杂,反映在有限元模型上,就是位于磨削弧内的单元既有热流输入又有对流换热作用属于混合边界条件。砂轮磨削工件视为移动热源。切深较小时,矩形移动热源更符合实际,切深较大时,通常采用三角形热源。本文采用矩形移动热源加载。
仿真软件ABAQUS自身不能直接加载移动热源,一些文献为解决热源“连续"加载问题,将总磨削时间离散设置多个分析步实现,操作麻烦,精度较低。
因此,本文借助ABAQUS提供的子程序DFLUX接口,由二次开发施加磨削移动热源,定义有限元仿真模拟的载荷边界条件。按照FORTRAN语言的语法编写程序代码,需完成必要的定义:①磨削区的定义;②热源运动的定义;③磨削弧热流密度和对流换热的定义。
3.5基于二次开发实现组织转变模拟
组织体积分数的计算,是计算模拟相变潜热、相变膨胀、相变应力的基础。CAE软件通常自身都不具备计算组织场功能。通常由二次开发实现。本文通过ABAQUS用户子程序接口USDFLD,运用Fortran语言将相变动力学理论编入代码,并在CAE计算中调用,在线获取任一节点任意时刻组织转变状况。
4成形磨削淬硬过程仿真分析
本文基于ABAQUS二次开发实现磨削淬硬温度场组织场仿真模拟。整个仿真计算过程分为两个分析步:磨削分析步和冷却分析步,磨削时间,即砂轮磨粒在工件表面作用的时间,可由下式计算得出:
而冷却时间为1000s,此时工件只受到空气对流换热作用。
4.1不同深度温度变化
磨削淬硬过程中,工件不同深度方向上(z向)温度变化和z向温度梯度曲线如图3和图4,任一时间点,z向的温度梯度都很大。距磨削区表面0.262mm以上的工件,在整个磨削淬硬过程中,最大温度均在Ac3(798.1℃)以上,意味着,它们将完全奥氏体化。距磨削区表面0.262mm与0.32mm之间的工件,在整个磨削淬硬过程中,最大温度均在Ac1(738.2℃)与Ac3之间,它们将发生部分奥氏体化。从某一深度层(z>0.32mm)开始,不会激活奥氏体转变。这取决于工件材料特性和磨削条件,包括砂轮转速,磨削深度,冷却速度等。
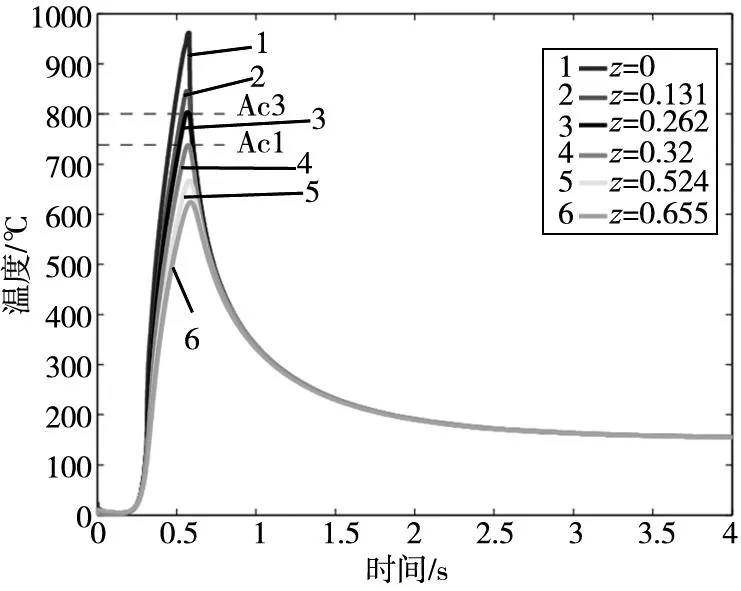
图3 不同深度磨削温度曲线
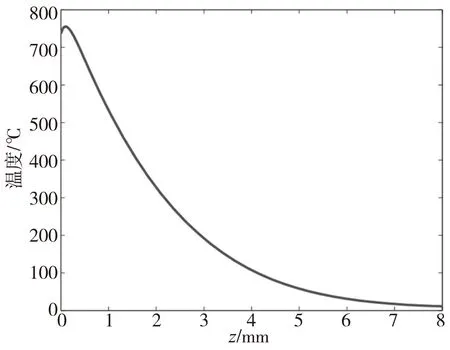
图4 z向温度梯度曲线
4.2组织转变曲线
42CrMo钢属于亚共析钢,初始组织主要为铁素体加珠光体。珠光体是共析铁素体和共析渗碳体有机结合的混合组织。如图5,当工件材料被加热至Ac1温度时,珠光体首先向奥氏体转变,奥氏体晶核在相界处形成,晶核不断长大并吞噬珠光体,随着温度的继续升高,奥氏体向铁素体中生长,最终转变为细小的奥氏体晶粒。奥氏体转变是一种逆共析过程,属于扩散型转变。磨削淬硬过程,升温速率很快,温度高,奥氏体转变迅速,由于最大温度超过Ac3温度,工件表层已完全奥氏体化,初始组织被转化。
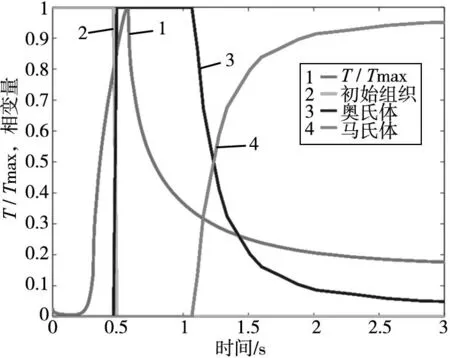
图5 组织转变曲线
马氏体组织最大的特点为高强度,高硬度,又有较好的韧塑性,因此,我们希望磨削淬硬后,齿轮最终组织为马氏体。要想获取更多马氏体,避免发生扩散型相变产生珠光体、贝氏体等组织,必须使工件快速冷却到Ms点。温度场仿真结果显示,工件温度从1000°下降至100°只需2s,冷速非常快,可以认为只发生非扩散型转变。温度降至Ms,马氏体转变被激活,随着工件表层温度持续降低,马氏体相体积分数不断增加,奥氏体相体积分数不断减少,此时为两相混合态。直至温度达到20°,马氏体转变结束,由图5可见,几乎所有奥氏体被转变为马氏体,磨削淬硬过程达到目的。
4.3淬硬层深度计算
钢的表面至内部马氏体组织占50%处的距离称为淬硬层深度。淬硬层越深,淬透性就越好。如果淬硬层深度达到心部,则表明该工件全部淬透。工件最大温度节点下方,不同深度层马氏体体积分数由CAE计算后如下表5所示,淬硬层深度约为0.291mm。

表5 不同深度层马氏体相变表
5结论
基于ABAQUS提供的子程序接口DFLUX,USDFLD,进行二次开发模拟仿真成形磨削淬硬过程的温度场,组织场。从仿真结果,可见得出:①磨削淬硬工件在磨削、切深方向的温度分布,判断是否激活相变;②工件在整个淬硬过程中的组织转变,计算出马氏体转变量;③计算淬硬层深度,评定磨削淬硬后工件的淬透性。
组织体积分数的计算,是计算模拟相变潜热、相变膨胀、相变应力的基础。温度场、组织场、应力场耦合仿真模拟是今后研究努力的方向。
[参考文献]
[1] Thai Nguyen1,L C Zhang.Realisation of grinding-hardening in workpieces of curved surfaces-part1:plunge cyclindrical grinding[J].International Journal of Machine Tools & Manufacture,2011,51:309-319.
[2] 马占龙,韩正铜.磨削淬硬温度场数值模拟与试验研究[J].中南大学学报(自然科学版),2012,43(3):960-965.
[3] 袁威,刘菊东.磨削条件对45钢最大磨削淬硬层深度的影响[J].现代制造工程,2013(1):84-87.
[4] 任敬心,华定安.磨削原理[M].北京:电子工业出版社,2011.
[5] Guo C,Optimation of eontinuous dress creep-feed form grinding proeess[J].CIRP Annals Manufac-turing Technology.2003(52):259-262.
[6] 陈勇平.平面磨削力建模及其应用研究[D].长沙:中南大学,2007.
[7] Rowe W B,Morgan M N.Simplified Approach to control of thermal damage in grinding[J].CIRP Annals Manufacturing Technology.1996,45(1):299-302.
[8] 牛山延.淬火冷却过程三维有限元模拟及工艺参数优化的研究[D].济南:山东大学,2007.
[9] A W Johnson,R F Mehl.Reactions of kinetics in processes of nucleation and growth[J]. Transactions of the American Institute of Mining,1939,135:416-458.
[10] M Avrami.Kinetics of phase change I,general theory[J].Journal of Chemical Physics, 1939,7: 1103-1112.
[11] E Scheil.Starting time of the austenite trans-formation[J].Eisenhuttenwes,1935,12:565-567.
[12] D F Koistien,R E Marburger. General equation Preseribing the extent of the anstensite transformation in pure iron-carbon alloys and Plain carbon steels[J].Acta Metallurgica, 1959,7: 50-60.
[13] 聂振国,石伟.应力影响42crMo钢马氏体相变的实验研究[C].第十次全国热处理大会论文集,2011.
[14] 陶文铨.传热学[M].西安:西北工业大学出版社,2006.
(编辑赵蓉)
Simulation Research on Temperature and Microstructure Field of Gear Form Grind-hardening
WANG Jie1,HONG Rong-jing1,ZHANG Jin2,FANG Cheng-gang1
(1.School of Mechanical and Power Engineering,Nanjing University of Technology,Nanjing 210009,China;2.Nanjing Gongda CNC Technology Co.,Ltd.,Nanjing 210009,China)
Abstract:In order to reflect the actual temperature and microstructure distribution during the form grind-hardening process,the temperature field of cooling process and the microstructure transformation was simulated by means of employing the ABAQUS secondary development according to FORTRAN rules for writing code and user subroutine interfaces (DFLUX,USDFLD) ,based on the mathematical model of thermodynamics and kinetics of phase transformation.The method can predict temperature changes in different directions and martensite distribution after grind-hardening.In addition,the hardened layer depth can be calculated which is the evaluation index of hardenability.The results show that, material 0.32mm below the surface will activate the transformation and the depth of hardened layers is about 0.291mm.The simulation plays a guiding role in the control of transformation of martensite in gear form grind-hardening process.
Key words:form grind-hardening; ABAQUS secondary development; temperature field; phase transformation
中图分类号:TH164;TG506
文献标识码:A
作者简介:王杰(1991—),男,南京人,南京工业大学硕士研究生,研究方向为成形磨齿机理,(E-mail)wj910129@126.com。
*基金项目:科技部科技型中小企业技术创新基金(13C26213202060)
收稿日期:2015-03-19;修回日期:2015-04-21
文章编号:1001-2265(2016)02-0026-04
DOI:10.13462/j.cnki.mmtamt.2016.02.008

