基于灵敏度分析的XK719数控铣床尺寸优化*
张疆平,李 想,贾成阁,赵希禄,关英俊
(1.长春工业大学 机电工程学院,长春 130012;2. 日本琦玉工业大学 工学部,日本 埼玉 369-1912)
基于灵敏度分析的XK719数控铣床尺寸优化*
张疆平1,李想1,贾成阁1,赵希禄2,关英俊1
(1.长春工业大学 机电工程学院,长春130012;2. 日本琦玉工业大学 工学部,日本 埼玉369-1912)
摘要:为了改善机床动静态特性,以XK719数控铣床为研究对象,采用Hypermesh软件建立数控铣床的有限元模型。在对铣床进行谐响应分析的基础上,得出机床1、2阶固有频率偏低的结论。运用灵敏度分析来寻找关键尺寸,并以关键尺寸为设计变量,以机床的质量和1、2阶固有频率为响应进行尺寸优化。最终,在铣床质量变化不大的情况下,使铣床的1阶固有频率提高了15.8%,2阶固有频率提高了11.3%。结果表明:该设计方法可以为机床零、部件的设计提供借鉴。
关键词:谐响应分析;灵敏度分析;尺寸优化
0引言
随着社会制造业的高速向前发展,机床正向着高速、高效、高可靠性、高柔性化和模块化的方向发展[1]。传统意义下的经验类比、静态分析的方法已无法满足当下机床的发展趋势。采用模态分析、谐响应分析等手段对机床的薄弱环节进行识别,运用各种优化手段对机床进行优化,使机床的结构设计趋于更加合理。随着技术的发展,各种优化方法也层出不穷,如当前的研究热点:拓扑优化[2]、基于响应面[3-4]和基于遗传算法[5]的优化方法。以及发展比较成熟的尺寸优化:如罗辉[6]对立柱进行动态性能灵敏度分析后,进行了多目标优化;郭垒[7]对立柱、滑板进行了结构灵敏度分析后,进行了轻量化设计;罗猛然[8]基于响应面法对床鞍进行了尺寸优化;Ming Cong[9]应用六西格玛分析手段寻找关键尺寸,对机床建立了模糊约束和模糊多目标函数,并进行了模糊多目标优化。但是,由于机床结构复杂,设计变量繁多,使设计变量与目标函数、约束之间的关系更加复杂,不利于优化,从而导致许多研究人员大多只对单个零件进行分析,很少对机床部件或整机进行分析。本文以XK719数控铣床为研究对象,基于灵敏度分析方法,采用尺寸优化这一比较成熟的优化方法对XK719数控铣床的部件进行有限元分析。
1建立模型
采用SolidWorks软件建立XK719数控铣床的立柱和主轴箱的三维实体模型,并将立柱和主轴箱的模型导入Hypermesh中,其模型如图1所示。
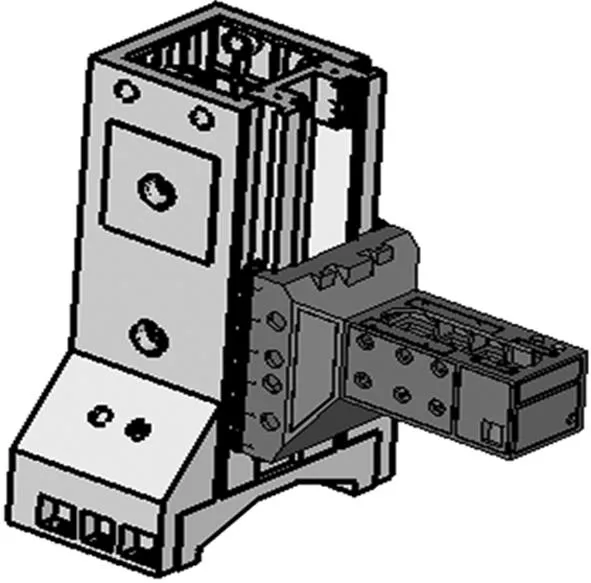
图1 立柱与主轴箱的三维实体模型
通过软件的网格划分工具,对于立柱、主轴箱的四壁以及筋板进行抽壳并采用壳单元进行划分;对于主轴箱压板、导轨镶条等结构采用六面体划分。由于立柱、主轴箱尺寸及结构特征差异大,因此对其采用不同的尺寸进行划分。立柱的平均尺寸为20mm,共得到28963个节点,单元数目为29236个;主轴箱平均尺寸为10mm,共得到68602个节点,单元数目为55311个。考虑到主轴箱压板、导轨镶条等六面体单元在内,总计共得131499个节点,单元数目为108262个。其有限元模型如图2所示。

图2 立柱与主轴箱的有限元模型
2谐响应分析
谐响应分析是用于确定线性结构在承受随时间正弦规律变化载荷时的稳态响应的一种技术[10]。该正弦规律的激励可以是激励力、激励位移或者是激励加速度。且这些激励可以来自外部环境,如地基引起的振动;也可以是由于内部情况,如旋转机械没经动静平衡检验而产生的离心力、往复运动机构的惯性力等。通过谐响应分析可进一步分析结构在多种激励下所产生的响应,防止共振现象的发生。
假设模型在简谐激励作用下,系统的运动微分方程为:
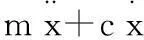
(1)
其通解由两部分组成:
x(t)=xc(t)+xp(t)
xc(t)=e-εwnt(Acoswdt+Bsinwdt)
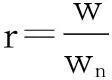
该(1)式的响应由两部分组成:xc(t)响应对应的是与结构具有相同频率振动的那一部分,该响应由于阻尼的存在,其信号会随着时间逐渐衰减为零,故称为“瞬态响应”。xp(t)响应对应的是与外加激励具有相同频率的那一部分,它与外加激励同存亡,故称为“稳态响应”。
本文基于对动静态分析的基础上(其中结构在静刚度满足要求的情况下,对系统进行模态分析,得1阶固有频率50.17Hz,2阶固有频率为54.63Hz,3阶固有频率为85.68HZ),对主轴箱夹持刀具的中心处施加X、Y、Z向的载荷,其幅值大小均为1000N,在立柱底面螺栓固定处施加全约束。考虑到模态分析的前7阶主振型,其简谐力设置的频率范围为0~100Hz。在此频率范围内施加简谐激励,该结构的响应曲线图如图3所示。该结构由HT300材料铸造成型,弹性模量E=1.3e5MPa,泊松比μ=0.25,密度ρ=7.4e-9t/mm3。
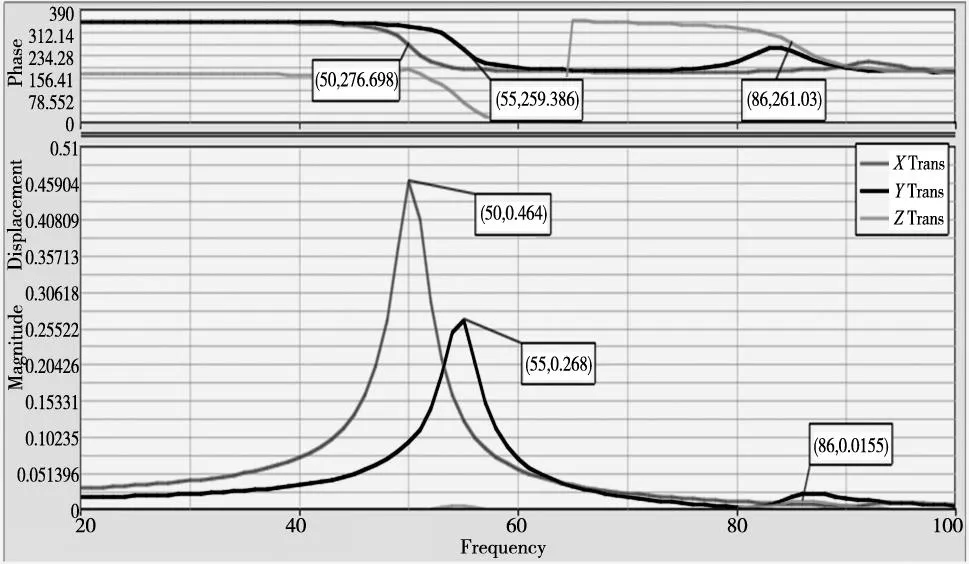
图3 立柱与主轴箱部件的谐响应分析
从图中立柱和主轴箱部件在外加简谐激励的作用下可知,刀具中心X轴方向在外加激励频率为50Hz时发生共振,振幅达0.464mm,对应的相位为276.698度,对比结构的固有频率可知,第1阶模态易在结构的X方向激发。刀具中心Y方向在外加激励频率为55Hz时发生共振,振幅达0.268mm,对应的相位为259.386度,对比结构的固有频率可知,第2阶模态易在结构的Y方向激发。刀具中心Z方向在外加激励频率为86Hz时发生共振,振幅比较小为0.01555mm,对应的相位为261.027度,对比结构的固有频率可知,第3阶模态易在结构的Z方向激发。结合加工条件可知,部件的第一、第二阶模态易落入外加激励的范围内,即意味着机床在外加激励的作用下易发生共振。故接下来的优化设计应考虑提高部件的第一、第二阶固有频率。
3灵敏度分析及优化设计
3.1灵敏度分析
有限元分析的目的就是为了进行结构优化,使结构趋于合理;灵敏度分析能够为结构优化设计做铺垫。灵敏度分析能够定量的计算出设计尺寸对性能指标的影响程度,从而寻求关键尺寸,为优化设计做铺垫。本次灵敏度分析研究,选取各零件的壁厚、筋板厚作为分析尺寸。各尺寸在结构中的位置简图如图4所示。各分析尺寸对应的名称、参数、初值、变化范围如表1所示。

图4 尺寸位置简图
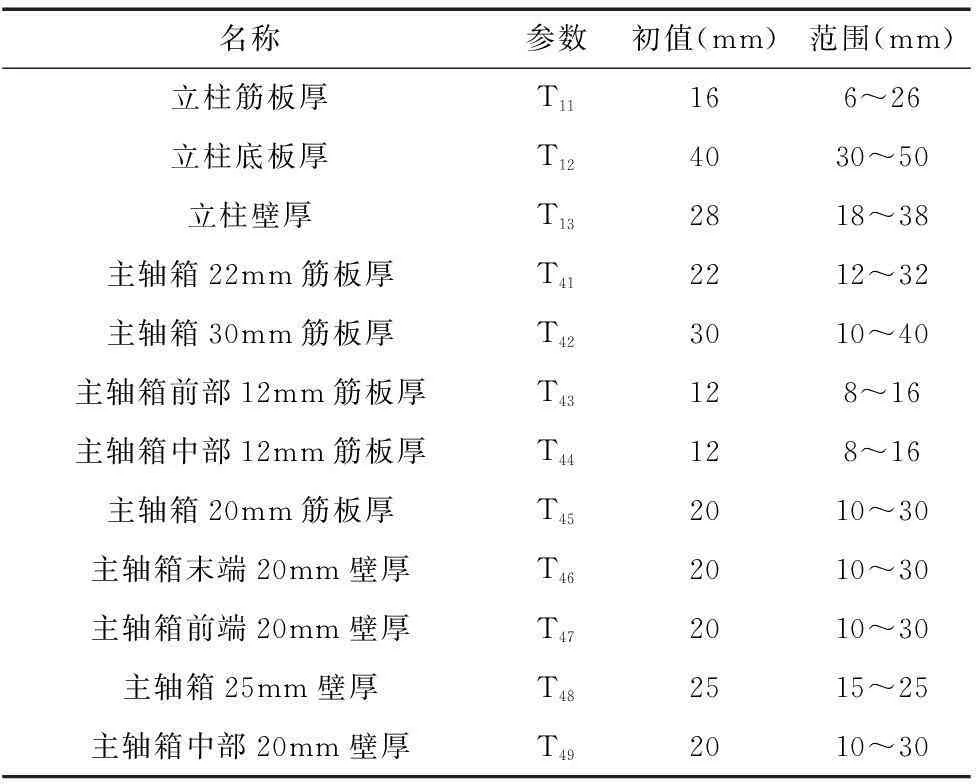
名称参数初值(mm)范围(mm)立柱筋板厚T11166~26立柱底板厚T124030~50立柱壁厚T132818~38主轴箱22mm筋板厚T412212~32主轴箱30mm筋板厚T423010~40主轴箱前部12mm筋板厚T43128~16主轴箱中部12mm筋板厚T44128~16主轴箱20mm筋板厚T452010~30主轴箱末端20mm壁厚T462010~30主轴箱前端20mm壁厚T472010~30主轴箱25mm壁厚T482515~25主轴箱中部20mm壁厚T492010~30
在对部件施加约束的情况下,利用Hypermesh中的control card sensitivity卡片,以部件的第1、2阶固有频率以及质量作为结构性能指标进行灵敏度分析,得各设计尺寸对结构性能的影响情况如图5~图7所示。
在灵敏度的图中,零刻度线以上表示随着设尺寸的增加或减小,结构对应的性能值越大或越小;反之,在零刻度线以下,随设尺寸的增加或减小,结构对应的性能值越小或越大。由图5可知,T11、T13对质量影响最大,且随着尺寸增加,质量增加越明显;T45、T46、T47、T48、T49的影响次之,且它们的值均在零刻度线上;T12、T41、T42、T43、T44对质量几乎无影响。由图6知,T11、T13、T47对 第1阶频率影响最大,其中随着T11、T13尺寸的增加,第1阶频率将提高,同时随着T47尺寸的增加,第1阶频率将降低;T45、T46、T48、T49的影响次之;T12、T41、T42、T43、T44对第1阶频率几乎无影响。由图7可知,T13、T47对第2阶频率影响最大,其中随着T13尺寸的增加,第2阶频率被提高,而随着T47的增加,第2阶频率将降低;T11、T45、T46、T49的影响次之;T12、T41、T42、T43、T44、T48对第2阶频率几乎无影响。
综合以上分析,本次优化设计将以T11、T13、T44、T45、T46、T47、T48、T49作为设计变量,对部件结构进行优化设计。
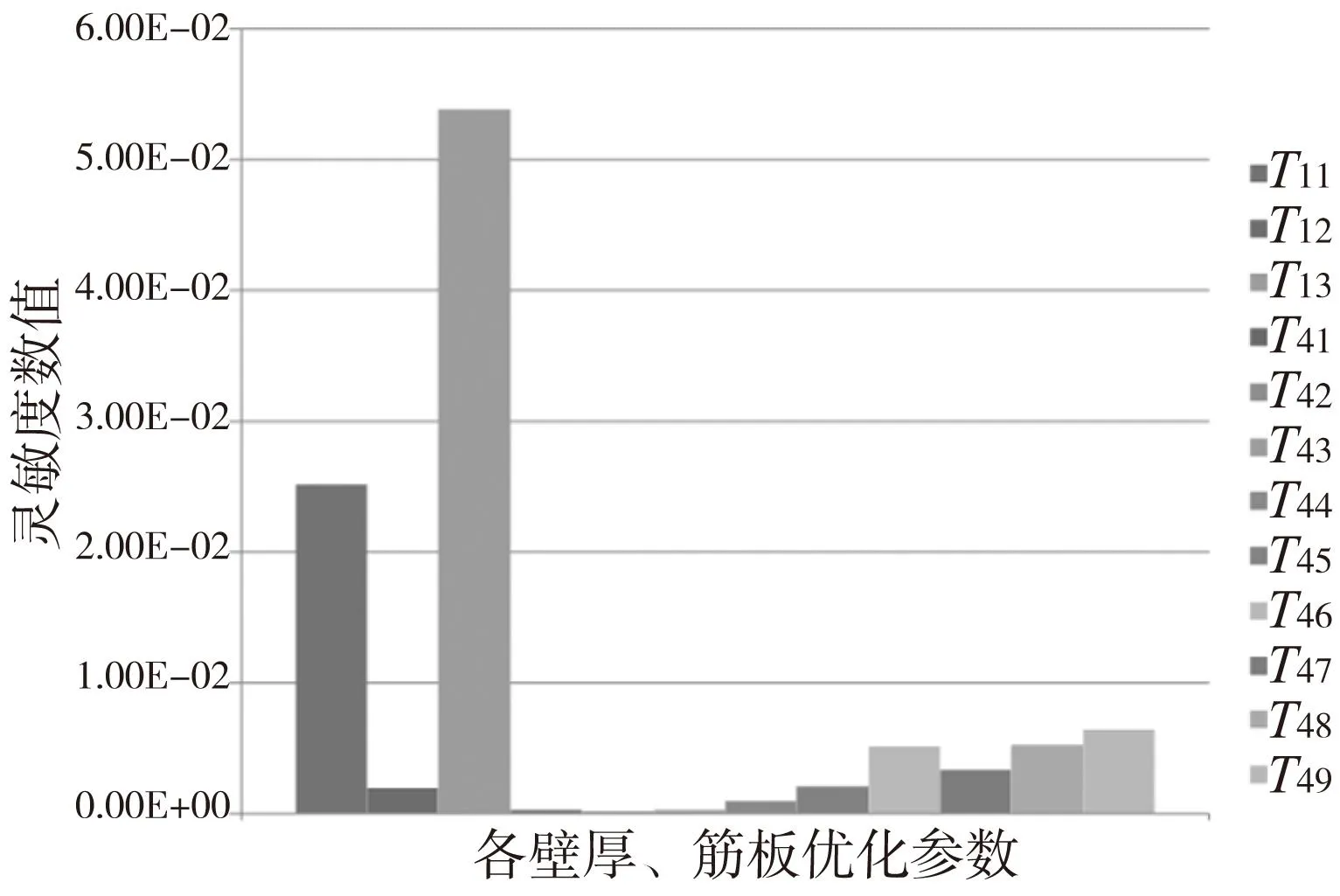
图5 对质量灵敏度分析
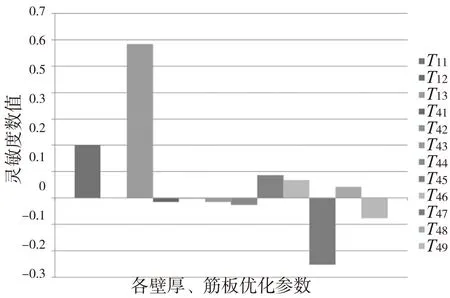
图6 对第1阶固有阶频率灵敏度分析
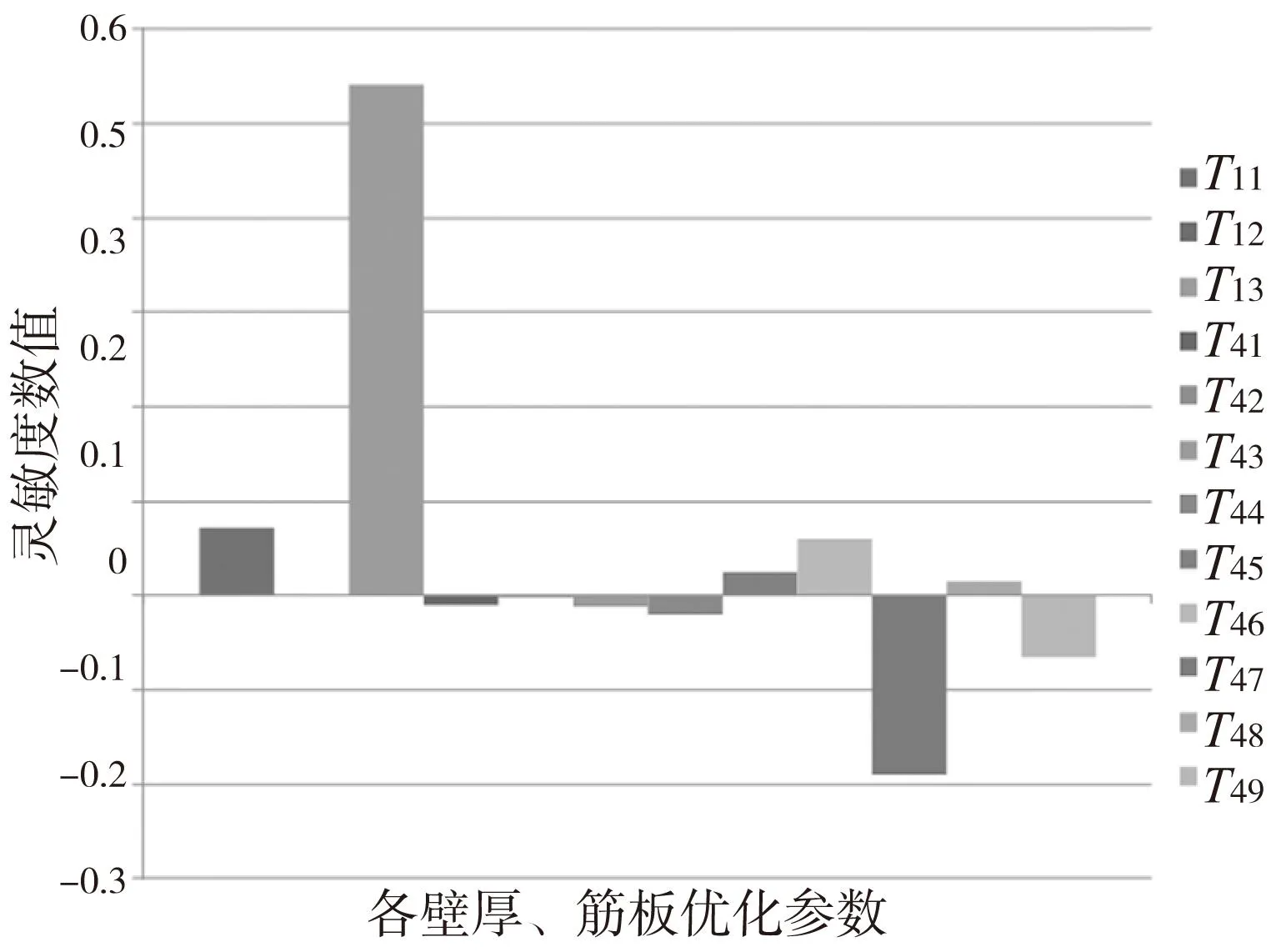
图7 对第2阶固有阶频率灵敏度分析
3.2优化结果分析
在灵敏度分析的基础上,应用Hypermesh中的Optistruct模块对部件进行优化。在通过多次优化实验基础上,以T11、T13、T45、T46、T47、T48、T49为设计变量(其中根据铸造工艺壁厚均匀的原则,将T46、T48、T49设为关联尺寸),得出以下三组方案。方案一:以mass<3,Freq>60为约束条件;以max Freq1为目标函数。方案二:以mass<3.2,Freq2>65为约束条件;以max Freq1为目标函数。方案三:以mass<3.2为约束条件;以max Freq1×0.6+Freq2×0.4为目标函数。通过对以上三种方案进行优化,得优化结果如表2所示。
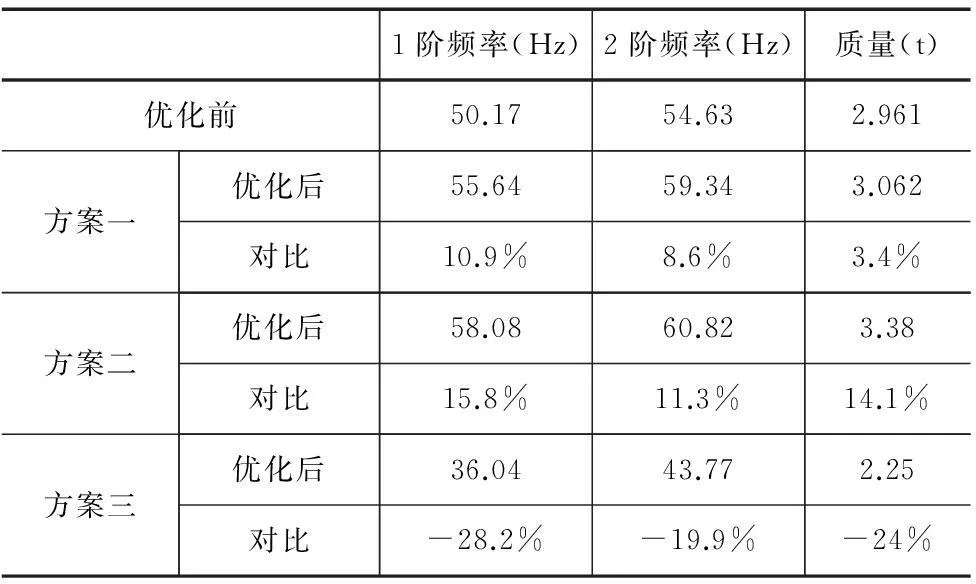
表2 优化结果
将所得优化尺寸进行圆整,并进行模态析态分析和谐响应分析,得圆整后的结果如表3和图8所示(其中方案一为图8中左上角响应图,方案二为右上角图)。
通过表3及图8分析可知:方案一的1阶固有频率增加10.9%,2阶固有频率增加8.6%,质量增加3.4%,在简谐激励的作用下X方向在1阶固有频率处发生共振,其振幅达0.476mm,增加2.6%;Y方向在2 阶固有频率处发生共振,振幅达0.308mm, 增加14.9%。方案二的1阶固有频率增加15.8%,2阶固有频率增加11.3%,质量增加14.1%,在简谐激励的作用下X方向在1阶固有频率处发生共振,其振幅达0.428mm,减少7.8%;Y方向在2 阶固有频率处发生共振,振幅达0.262mm,减少2.2%。方案三的1阶固有频率增加28.2%,2阶固有频率增加19.9%,质量减少24%,在简谐激励的作用下X方向在1阶固有频率处发生共振,其振幅达0.767mm,增加65.3%;Y方向在2 阶固有频率处发生共振,振幅达0.404mm, 增加50.8%。考虑上述数据知,方案一虽然质量增幅不大,但1、2阶固有频率增幅也不大,且在简谐力作用下振幅变大;方案二,虽牺牲了一定的质量,但1、2阶固有频率都有较大的增幅,且在简谐力作用下振幅变小;
方案三,虽然质量大幅减小,频率可以有效避开实际工作频率,但由于部件刚度减弱,振幅急聚增大。故综合考虑,选择方案二为最优化结果。
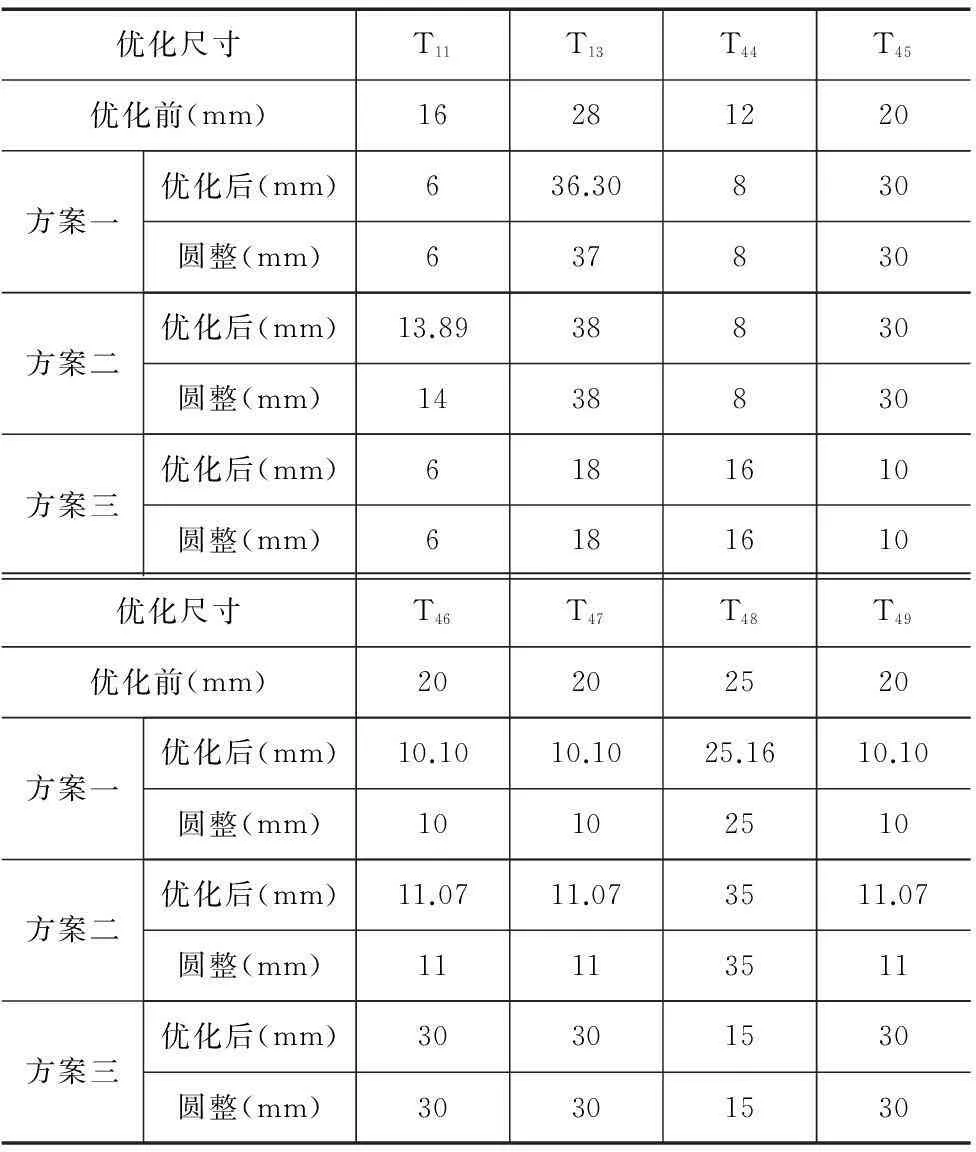
表3 结果对比
4结论
应用有限元软件对结构部件进行有限元划分,通过谐响应分析,发现机床的1、2阶固有频率有待提高。基于灵敏度分析,得到对机床性能指标关键尺寸。将所得关键尺寸定义为设计变量,将质量、1阶固有频率以及2阶固有频率作为响应(此处的响应包括约束和目标函数),对部件进行尺寸优化。通过设定多种方案,并对方案优选的情况下,得到第二种方案。通过数据分析可得,机床在质量变化不大的情况向下,1阶固有频率增加了15.8%,2固有频率增加了11.3%。结果表明,该设计手段能够为机床的分析设计提供重要的参考。
图8 优化谐响应分析
[参考文献]
[1] 王泽林.机床滑动结合面特征参数识别分析与研究[D].北京:北京工业大学,2011.
[2] 杜义贤,严双桥,周俊雄,等.数控插齿机床的静动多目标拓扑优化设计[J].机械设计,2014,31(6):64-67.
[3] 姜衡,管贻生,邱志成,等.基于响应面法的立式加工中心动静态多目标优化[J].机械工程报,2011,47(11):125-133.
[4] 王万金,殷国富,胡腾,等.基于网格变形技术和响应面模型的机床床身优化方法[J].组合机床与自动化加工技术,2014(7):5-8.
[5] 申远,金一,褚彪,等.基于遗传算法的锻压机床多目标优化设计方法[J].中国机械工程,2012,23(3):291-294.
[6] 罗辉,陈蔚芳,叶文华.机床立柱灵敏度分析及多目标优化设计[J].机械科学与技术,2009,28(4):487-491.
[7] 郭垒,张辉,叶佩青,等.基于灵敏度的机床轻量化设计[J].清华大学学报,2011,51(6):846-850.
[8] 罗孟然,丛明,王德胜,等.基于响应面的数控机床床鞍尺寸优化[J].组合机床与自动化加工技术,2014(9):6-10.
[9] Ming Cong,Tao Han,Qiang zhao.FuzzyMulti-Objective Optimization of Sliding Rack Based on Six Sigma and Goal Driven[J].Mechanic Automation and Control Engineering,2010:556-559.
[10] 李涛,马春翔. MB4250-2高精度立式珩磨机床动态特性分析[J].机械设计与制造,2008(11):163-165.
[11] 杨玉萍,张森,季彬彬,等.龙门加工中心横梁关键尺寸灵敏度分析与优化[J].制造业自动化,2013,35(8):110-113.
[12] 邱海飞.数控机床床身结构动力学优化与谐响应分析[J].现代制造工程,2014(4):52-56.
[13] 周德繁,高炳微,智政.重型龙门镗铣床横梁有限元分析与结构优化[J].哈尔滨理工大学,2013,18(2):72-76.
[14] 于海莲,王永泉,陈花玲,等.响应面模型与多目标遗传算法相结合的机床立柱参数优化[J].西安交通大学学报,2012,46(11):80-85.
[15] 张勇,李光耀,钟志华,等.基于移动最小二乘响应面方法的整车轻量化设计优[J].机械工程学报,2008,44(11):192-196.
[16] G Gary Wang.Adaptive Response surface Method Using Inherited Latin Hypercube Design Points[J].Journal of Mechanical Design,2003,125(2):210-220.
[17]关英俊,赵扬,任利利,等.XK2425/5L五轴龙门铣床主体结构有限元分析[J].组合机床与自动化加工技术,2010(12):5-9.
(编辑赵蓉)
Size Optimization of XK719 CNC Milling Machine Based on Sensitivity Analysis
ZHANG Jiang-ping1, LI Xiang1,JIA Cheng-ge1,ZHAO Xi-Lu2,GUAN Ying-Jun1
(1.School of Mechatronic Engineering,Changchun University of Technology,Changchun 130012,China;2.Department of Engineering,Saitama Institute of Technology,Saitama 369-1912,Japan)
Abstract:In order to improve static and dynamic characteristics of machine tools,hypermesh software was adopted to establish the finite element model of CNC milling machine with the XK719 CNC milling machine as the research object.On the basis of the harmonic response analysis for milling machine,it was concluded that the first and second natural frequency were low.Using the method of sensitivity analysis found the key dimensions.And the size optimzation was carried out where the key dimensions was defined as design variables and the mass of the machine tool,the first natural frequency and the second natural frequancy were defined as responses.Finally,under the conditions of little change of milling machine’s mass,this method made the first natural fraquency increased by 11.5% and the second natural frequancy increased by 11.3%.Results showed that the design method provided reference for the design of the parts and components.
Key words:harmonic response analysis;sensitivity analysis;size optimization
中图分类号:TH122;TG659
文献标识码:A
作者简介:张疆平(1990—),男,江苏张家港人,长春工业大学硕士研究生,研究方向为CAD/CAM及结构优化设计,(E-mail)1791874561@qq.com;通讯作者:关英俊(1978—),男,满族,吉林永吉人,博士,长春工业大学副教授,硕士生导师,研究方向为机械CAD/CAE及结构优化,(E-mail)gyj5460@sohu.com。
*基金项目:教育部"春晖计划" 资助项目(20130012)
收稿日期:2015-04-11;修回日期:2015-05-10
文章编号:1001-2265(2016)02-0005-04
DOI:10.13462/j.cnki.mmtamt.2016.02.002

